网络流模型

网络流模型

与2sat：2sat求不了最值，但网络流可以。

\(n\le 200 \implies\) 网络流

二分图、最大流模型

• 二分图匹配模型——左右两侧匹配

• 长脖子鹿模型——找到奇偶性，二分化

• LNDSP模型（P2766）——左右二分图来回跳

最小割模型

（无穷大的边表示强限制）

• 类2sat模型——要么属于左，要么属于右（2sat求不了最值，但网络流可以）。

• 切糕模型——关于变量取值，建立两条链之间限制，我们将一个变量取值建成的链叫做这个变量的 \(s\to t\) 链

  

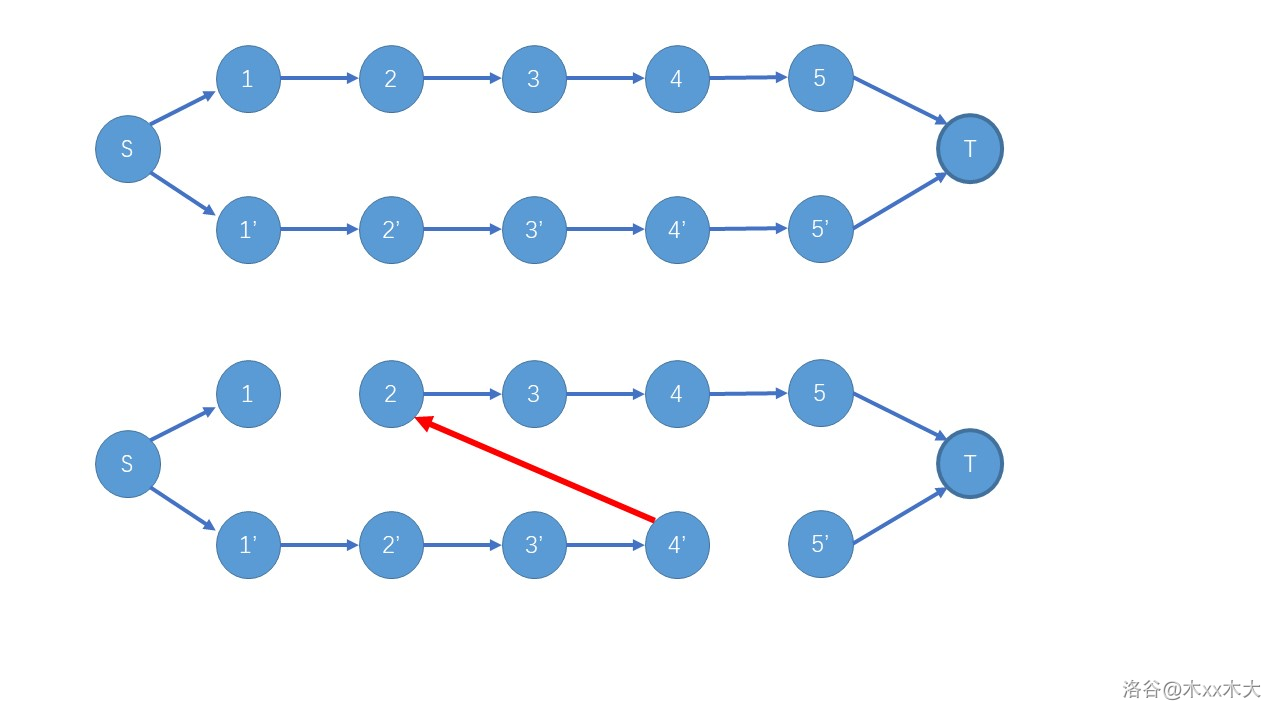
  切糕模型防割多边限制：向前建 \(+\infin\) 的边（P6054）

  不然一下情况：

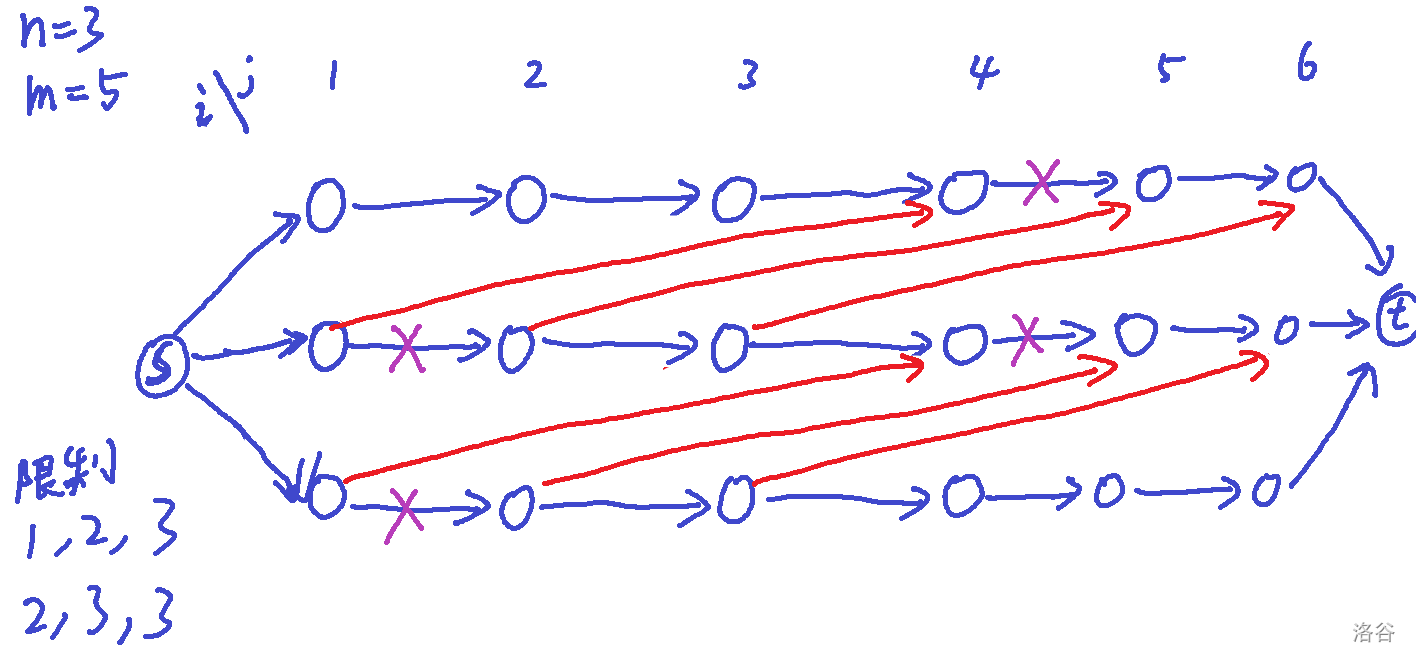
  共同限制：

  

  (x1,x2,x3,y1,y2,y3) 分别是不同变量 \(s\to t\) 链上的点。

  表示若 \((a_1\ge x_1\lor a_2\ge x_2\lor a_3\ge x_3)\land (b_1\le y_1\lor b_2\le y_2\lor b_3\le y_3)\) 则再贡献 \(w\) 的权值，\(w=+\infin\) 表示上述条件不能成立。

• 文理分科模型——若同时有……则有……

  

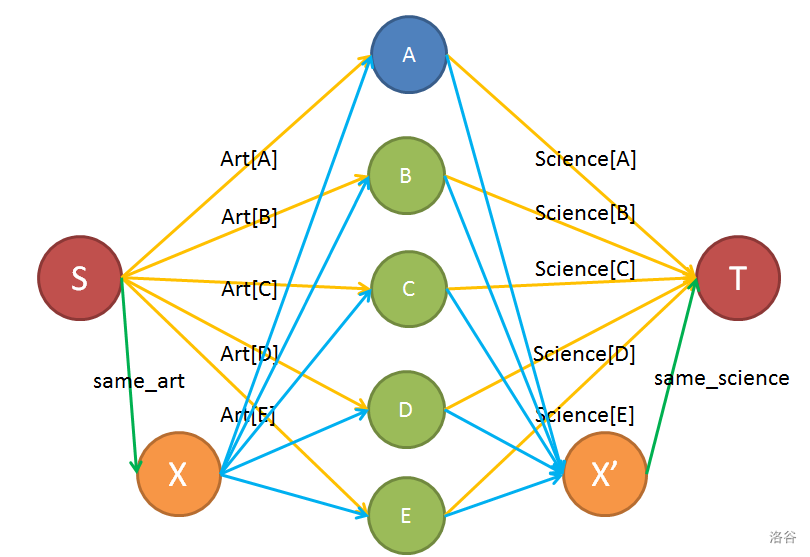
• YAMP（CF903G）模型——以最小割求最大流，适用于特殊的图上问题

费用流模型

（最大流保证合法，费用计算价值）

• 语文作业模型——选择贡献价值，不选收到限制。建立一条链。

• 多次方格取数模型——拆点建多种不同的边，以限制选取次数。

• 建一维点：如果一个元素的贡献会随着前面的选择而变化，可以把所有可能的贡献全部建出来进行限制，相当于升维。P2053 [SCOI2007] 修车

• 拆贡献，将平方变为累加。

• 最大权闭合子图问题——正点权和−绝对值最小割

• 费用流+二分：限制网络流的流量，从而看费用是否满足，达到先满足费用，再满足流量。P4068 [SDOI2016] 数字配对

有负环费用流：强制满流P7173

上下界模型

可行流

无源汇

令 \(in_u\) 为入边下界和，\(out_v\) 为出边下届之和。\(\forall u|in_u>out_u,S\to u,\forall u|in_u<out_u,u\to T,c'(x,y)=c(x,y)-b(x,y)\) 跑最大流，看是否满流。

有源汇

加 \((T',S',\infin)\) 的边变为上者。

有源汇最值流

先找到一个可行流，删去 \((T',S',\infin)\) 的边。

最大流

原来可行流的流量加上残量网络上跑 \(S\to T\) 的最大流（增流）。

最小流

原来可行流的流量减去残量网络上跑 \(T\to S\) 的最大流（退流）。

覆盖、匹配、独立集

最小边覆盖\(+\)最大匹配\(=|V|\)，最小点覆盖\(+\)最大独立集\(=|V|\)。

有向图链覆盖——建立两个关系，化有向为无向链接关系。

Hall定理

---

网络流不能想着限制边的流法，只能通过建图的方法解决。