数据结构-黄洛天

数据结构-黄洛天

A - 冰火战士

题面

支持\(Q\)次两种操作，

• 添加一个三元组 \((w,a,b),w\in\{0,1\}\)
• 撤回第 \(k\) 此操作，此操作保证为报名信息

每次操作后，求

\[\max_{x}\min(\sum_{w_i=0,a_i\le x}b_i,\sum_{w_i=1,a_i\ge x}b_i) \]

以及取到最值的最大的 \(x\)。

\(1\le Q\le 1\times 10^6,1\le x\le 2\times 10^9,不存在相同的三元组\)

题解

有一个很显然的\(\mathcal O(n\log^2n)\) 做法，即对每个 \(w\in\{0,1\}\) 开一个树状数组，每次二分查找 \(x\)，并判定 \(\sum_{w_i=0,a_i\ge x}b_i-\sum_{w_i=1,a_i\le x}b_i\) 的正负，使其最接近 \(0\)，确定了值之后，再倍增求得 \(x\) 。

考虑优化，我们发现，树状数组上的 \(p\) 号节点存储的恰为 \([p-\operatorname{lowbit}(p)+1,p]\)，利用这一点，我们可以在倍增的过程中不断同步累加树状数组中的值，从而优化掉一个 \(\log\)。

当从 \(p\) 倍增到 \(p+2^i\) 次方时，由于\(\operatorname {lowbit}(p)>2^i\) ，所以我们只需要加上 \(bitr[p+2^i]\) 查看是否合法即可。

复杂度 \(\mathcal O(n\log n)\)。

方法

• 倍增同时 \(O(1)\) 查询树状数组中的值。

代码

链接

B - Fenwick Tree

题面

有一个长度为 \(n\) 的树状数组，给出在进行了若干次单调修改操作后每个位置存储的值是否非 \(0\)，求最少进行了几次修改操作。

\(1\le n\le 10^5\)

题解

每次修改相当于给某个点到根加一个数字。

我们从低向上考虑整个树，依次判断是否要给当前节点操作。假设他有 \(k\) 个儿子是大于 \(0\) 的。

• \(k = 0\)，子树内所有操作对于我的影响是 \(0\).

• \(k = 1\)，子树内所有操作对于我的影响一定非 0

• \(k > 1\)，子树内所有操作对于我的影响是任意的。

因此只有 \(k = 0\) 且目标是 \(1\) 的时候需和 \(k = 1\) 且目标是 \(0\) 的时候要进行操作。 时间复杂度 \(\mathcal O(n)\)。

方法

• 考虑贡献

  整体考虑子树对父亲的贡献。

C - Traveling in Cells

题面

有 \(n\) 个二元组 \((c,v)\) ，支持 \(q\) 次三种操作

• \(1\ p\ x\)：将 \(c_p\) 修改为 \(x\)

• \(2\ p\ x\)：将 \(v_p\) 修改为 \(x\)

• \(3\ p\ k\ a_{1\sim k}\)：求 \(\max\limits_{p\in [l,r]}\sum\limits_{\forall i\in[l,r],c_i\in\{a_1,a_2,\cdots,a_k\}}v_i\)

\(1\le n\le 10^5,1\le q\le 10^5,\sum k\le 10^6\)

题解

对于每一个 \(c\) 建立一颗线段树维护区间个数，前两个操作就是单点修改，第三个操作结合树状数组求解。

对于第三个操作，本质上是找到左与右第一个的没有出现在 \(a\) 中的 \(c\) ，只需要看这些颜色是否铺满一个区间便是，代码如下：

int RP(vector<int> u,int pos,int L=1,int R=n){
    if(Cnt(u)==R-L+1)return n+1;
    if(L==R)return L;
    int mid=L+R>>1;
    if(pos<=mid){
        int res=RP(lson(u),pos,L,mid);
        return res==n+1?RP(rson(u),pos,mid+1,R):res;
    }else{
        return RP(rson(u),pos,mid+1,R);
    }
}
int LP(vector<int> u,int pos,int L=1,int R=n){
    if(Cnt(u)==R-L+1)return 0;
    if(L==R)return L;
    int mid=L+R>>1;
    if(pos>mid){
        int res=LP(rson(u),pos,mid+1,R);
        return res==0?LP(lson(u),pos,L,mid):res;
    }else{
        return LP(lson(u),pos,L,mid);
    }
}

方法

• 最近元素查找模型——线段树左右第一个查找法，代码与上类似

D - k-Maximum Subsequence Sum

题面

长度为 \(n\) 的数列，支持两种操作：

1. 修改某个位置的值。

2. 询问区间 \([l,r]\) 里选出至多 \(k\) 个不相交的子段和的最大值。

一共有 \(m\) 个操作。

题解

要求 \(k\) 个不交的，那么可以先求出最大子段和，假设区间为 \([l, r]\)，然后给区间 \([l, r]\) 内的所有元素取相反数，也就代表着此后你要是不想选这个数，那么就取一遍相反数抵消掉，以此类推做 \(k\) 轮。

线段树需要维护：区间和，前缀和最大值，后缀和最大值，区间和最大值，前缀和最小值，后缀和最小值，区间和最小值，以及每种最大最小值取到的方案。

时间复杂度 \(\mathcal O(n \log n)\)。

方法

• 线段树结合贪心

代码

链接

E - Max Mex

题面

给定一棵有 \(n\) 个点的树，每个节点有点权。所有的点权构成了一个 \(0~\sim~n - 1\) 的排列。有 \(q\) 次操作，每次操作 \(1\) 为交换两个点的点权，操作 \(2\) 为查询 \(Mex(l)\) 值最大的 \(Mex(l)\) 值，其中 \(l\) 是树上的一条路径。定义一条路径 \(l\) 的 \(Mex\) 值 \(Mex(l)\) 为这条路径上最小的没有出现过的自然数

\(2\le n\le 2\times 10^5,1\le q\le 2\times 10^5\)

题解

考虑使用线段树维护维护值域，也就是对于值域区间 \([l, r]\) 的点，他们在树上的位置能否组成一条链，如果可以这个链的端点是谁。合并的时候分类讨论。

查询时记录当前维护值域之前的信息，进行合并

方法

• 线段树维护其他信息

  线段树不一定维护数值信息，只要是有结合律的操作都可以，比如本题的合并。

代码

链接

F - The Fair Nut's getting crazy

题面

给定序列 \(\{\alpha\}\)，求有多少个四元组 \((a,b,c,d)\) 满足以下条件

1. \(a<c\le b<d\)

2. \(\forall i\in[c,b],\forall j\in[a,d],\exist!i=j,\alpha_i=\alpha_j\)

解法

令 \(pre_i=\max\limits_{\alpha_j=\alpha_i,j<i}j,nxt_i=\max\limits_{\alpha_j=\alpha_i,j>i}j\)

则对于一个合法四元组 \((a,b,c,d)\)，有 \(\max\limits_{i=c}^bpre_i<a<c\le b<d<\min\limits_{i=c}^bnxt_i,\)

易得最远情况下， \(a=\max\limits_{i=c}^bpre_i+1,d=\min\limits_{i=c}^bnxt_i-1\)

所以 \(\max\limits_{i=c}^bpre_i+1<c\le b<\min\limits_{i=c}^bnxt_i-1\)

这关乎两个变量，所以假设我们枚举 \(c\) 则答案 \(b\) 的选取具有单调性

当 \(b\) 去到最远时，答案为 \(\sum\limits_{i=c}^b(c-\max\limits_{j=c}^ipre_j-1)(\min\limits_{j=c}^inxt_j-1-i)\)

由于计算的下边界都是 \(c\) 考虑倒序枚举，动态维护上式

展开得：\(\sum\limits_{i=c}^b (c-1) * \min\limits_{j=l}^inxt_i - (c-1)*(i+1) - \max\limits_{j=c}^ipre_j * \min\limits_{j=c}^inxt_j + \max\limits_{j=c}^ipre_j * (i+1)\)

用线段树分别维护即可

抽象化方法

• 先数学化，再推导

• 多变量关联情况——枚举+维护

  如上式中会出现一个同时与 \(b,c\) 相关的式子，我们可以考虑枚举一个，维护一个

• 维护法——拆式子

  将式子拆开，分别维护每一部分，要比维护整体更简单

G - Useful Algorithm

题面

定义 \(val(a,b)=\max\limits_{\{i|a+b在二进制的第i为下进位\}}w_i\)，例如 \(\because 5+3=101_2+11_2=1000_2，所以val(5,3)=\max(w_1,w_2,w_3)\)

给定长度为 \(n\) 的序列 \(\{c\}\) 和 \(\{d\}\)，求\(\max\limits_{i,j}val(i,j)\times(d_i+d_j)\)，并支持单点修改 \(c,d\)

\(1\le m\le 16,1\le c_i\le 2^m,1\le n\le 10^5,1\le d\le 10^9\)，强制在线

解法

\[\begin{aligned} &\max\limits_{a,b}\max\limits_{\{i|a+b在二进制的第 i 位进位\}}w_i\times(d_a+d_b) \\=&\max\limits_{i}w_i\max\limits_{\{a,b|a+b在二进制的第 i 位进位\}}d_a+d_b \\&令A=a\bmod 2^i,B=b\bmod2^i,f_A=\max_{i\bmod 2^i=A} d_i \\=&\max_iw_i\max_{A+B\ge 2^i}f_A+f_B \\&令g_A=f_{2^i-A} \\=&\max_iw_i\max_{A\le B}g_A+f_B \end{aligned} \]

对于每一位维护一棵线段树即可

抽象化方法

• \(a+b\ \ \ \ p\) 进制下第\(i\) 位进位是指 \(a\bmod p^i+b\bmod p^i\ge p^i\)

• 拆式子——交换内外循环

  本题中将外循环变为每一位，内循环变为数，以简化处理

• 形如 \(a\cdot b\ge C的卷积\)，可以化为 \(C\cdot \overline{b}\le a\)，用线段树进行维护

  二元运算 \(\cdot\) 可以为 \(\oplus+\times\)等存在逆元的运算

H - Vacation

题面

给定序列 \(a_{1\sim n}\)， \(m\) 个操作，与一个限制 \(c\) 。

单点修改，查询区间中长度不超过 \(c\) 的最大子段和。

\(1\le c\le n\le 2\times 10^5,1\le m\le 5\times 10^5,-10^9\le a_i\le 10^9\)

题解

参考题解：GYM103861F 解题报告

先将序列按照长度 \(c\) 分块。

最终答案仅可能来自于两种情况

• 属于一个块

• 跨过至两块

对于第一种情况，我们直接维护一个普通的最大子段和。

对于第二种情况：答案一定由一个后缀加上一个前缀组成。令 \(l,r\) 表示左右端点在其各自段中的编号，易得 \(l\ge r\) 。所以我们去维护 \(\max pre_x,\max suf,\max_{x>y}suf_x+pre_x\) 就行了（其中 \(pre\) 表示这一段的前缀，\(suf\) 表示前一段的后缀）。

所以说，我们需要维护三种线段树

• 维护最大字段和

• 对于每一块，维护与前一块 \(pre,suf\) 拼接情况

• 对于全局，维护前两种线段树在考虑完整段时的答案

下面是具体操作：

修改

修改整棵最大子段和线段树的答案并更新维护答案的线段树

对前面块的后缀和进行前缀加并更新维护答案的线段树

对后面块的前缀和进行后缀加并更新维护答案的线段树

查询

令 \(L,R\) 表示左右端点 \(k_l,k_r\) 为左右端点所在的块， \(l,r\) 分别为左右端点的块内编号。

• 当 \(R-L+1\le c\) 直接询问最大子段和

• 当 \((R-L+1>c)\land(k_r=k_l+1)\)，此时将一个块分为了三个部分 \([1,l),[l,r],(r,c]\)，答案来自于三种情况。

  • \(\max_{l\le y<x\le c}suf_x+pre_y\)

  • \(\max_{x\in [1,l)}pre_x+\max_{x\in [l,c]}suf_x\)

  • \(\max_{x\in [1,r]}pre_x+\max_{x\in(r,c]}suf_x\)

  取最大值即可。

• 当 \((R-l+1>c)\land(k_r>k_l+1)\)，答案来自于两种情况

  • 中间部分，即 \(k_l+1\sim k_r-1\) 中的整段最大子段和同 \(k_l+1与k_l+2,\cdots,k_r-2与k_r-1\) 中的完整跨段关系。

  • 两边部分，转化为两个情况二。

时间复杂度 \(\mathcal O((n+m)\log n)\)

方法

• 分段维护线段树

• 将两端之间有关联的信息放入一个线段树进行处理。

J -  Game: Celeste

题面

数轴上有 \(n\) 个点，第 \(i\) 个点的坐标为 \(x_i\)，权值为 \(a_i\)。小 A 可以从 \(x\) 跳到 \([x+L,x+R]\) 的一个位置，跳到一个位置会拾取当前位置上权值，他想从第 \(1\) 个点跳到第 \(n\) 个点，并使得拾取权值的集合单调不增排列后的字典序最大。若不能到达，输出 \(-1\)。

\(\forall i\in[1,n-1],x_i<x_{i+1}<10^9，1\le a_i\le n\le 10^5,1\le L,R\le 10^9\)

解法

用线段树维护所选集合。考虑单调队列优化 DP。

按照字典序每次选出最“大”的集合，转移就是以此版本为基础建立可持久化线段树。

比较集合大小就用线段树上二分，如果 \(root[n]=0\)，则不能到达。

抽象化方法

• 维护集合——权值线段树

• 可持久化数据结构——一种转移关系

  所以可以用来DP

• 数据结构比大小，定义其大小关系，以便用在\(\min,\max\) 等情境中。

K - 道路建设

题面

给定平面上 \(n\) 个点的坐标，求前 \(k\) 小的点曼哈顿距离之和。

\(2\le n\le 2.5\times 10^5,1\le k\le \min(2.5\times 10^5,\frac {n(n-1)}{2})\)

题解

为了方便先离散化，把 \(x, y\) 均离散化成不同的。

因为 \(k\) 比较小，考虑对于每个点求出右侧距离他最近的点，然后把这些距离扔到一个堆里，每次取出最小值。最小值对应的点为 \(u\)。把距离 \(u\) 第二近的点的距离和 \(u\) 扔到堆里。

因为我们限定了只考虑横坐标在一个点 \((x',y')\) 右边的点 \((x,y)\)。

• 当 \(y>y'\) 时，\(|x-x'|+|y-y'|=(x+y)-(x'+y')\)

• 当 \(y<y'\) 时，\(|x-x'|+|y-y'|=(x-y)-(x'-y')\)

所以查询距离 \((x',y')\) 最近的点只需要查询 \([1,y')\) 里的 \(x-y\) 的最小值和 \((y'n]\) 内 \(x+y\) 的最小值

考虑从右到左扫描线，用主席树维护区间 \(y + x\) 的最小值和 \(x − y\) 的最小值，每次加入一个点。

如果要找第二小值，就把第一小值对应的 \(y\) 的地方设为正无穷即可。注意为了不影响其他点的线段树，这里也需要可持久化（即新建节点）。

方法

• 离散化

  在离散化时去重就是相同对相同，在离散化的时候不去重并加上标记就是相同对不同，这样离散为不同有助于许多情况的简化。

• 可持久化的修改

  新建节点——再次可持久化，以避免对后续版本造成影响。

• 扫描线

  从一个方向至另一个方向的动态线段树信息就是扫描线，这样确定了一个枚举（处理）顺序，方便处理

L - 树

题面

给定一棵 \(n\) 个结点的有根树 \(T\)，结点从 \(1\) 开始编号，根结点为 \(1\) 号结点，每个结点有一个正整数权值 \(v_i\)。

设 \(x\) 号结点的子树内（包含 \(x\) 自身）的所有结点编号为 \(c_1,c_2,\dots,c_k\)，定义 \(x\) 的价值为：

\( val(x)=(v_{c_1}+d(c_1,x)) \oplus (v_{c_2}+d(c_2,x)) \oplus \cdots \oplus (v_{c_k}+d(c_k, x)) \)

其中 \(d(x,y)\) 表示树上 \(x\) 号结点与 \(y\) 号结点间唯一简单路径所包含的边数，\(d(x, x) = 0\)。\(\oplus\) 表示异或运算。

请你求出 \(\sum\limits_{i=1}^n val(i)\) 的结果。

\(1\le n,v_i\le 525010\)

题解

将 \((v_{c_i}+d(c_i,x))\) 看作一个数，我们发现这实质上是要支持三种操作——合并子树信息、全局加一与插入一个值，维护一种信息——全局异或和。由于是二进制信息，这里考虑0/1字典树，合并子树信息与插入一个值都很简单。

考虑如何全局加一。

我们发现对一个数加一在二进制下的步骤可以解释为，找到最低为的 \(0\) 将其赋为 \(1\) 并将那些位数比它低的 \(1\) 复制为 \(0\)。

回到这颗0/1树上，可以解释为先交换一个节点两条边下面的两棵子树，再向交换后的 \(0\) 边进行递归操作，这样一次复杂度为 \(\mathcal O(\log v)\)

考虑维护异或值，我们可以考虑每条边的贡献。如果一条 \(1\) 边的子树中有奇数个值时，累计这个一，否则不累计，每次维护 \(\mathcal O(1)\)。

时间复杂度 \(\mathcal O(n\log v)\)

方法

• 01-trie 可以用来维护一些数字的异或，支持修改

  其插入、删除、全局加一、全局减一（从递归 \(0\) 边变为递归 \(1\) 边）、合并操作都十分常见。注意

M - 众数

题面

定义众数为序列中出现次数严格大于一半的数字。

一开始给定 \(n\) 个正整数序列，编号为 \(1 \sim n\)，初始序列可以为空。

有 \(q\) 次操作，操作有以下类型:

• \(1 \ x \ y\)：在 \(x\) 号序列末尾插入数字 \(y\)。
• \(2 \ x\)：删除 \(x\) 号序列末尾的数字。
• \(3 \ m \ x_1 \ x_2 \ x_m\)：求 \(x_1, x_2, \ldots, x_m\) 合并后的众数。不存在返回 \(-1\)。询问中的合并操作不会对后续操作产生影响。
• \(4 \ x_1 \ x_2 \ x_3\)：新建一个编号为 \(x_3\) 的序列，其为 \(x_1\) 号序列后顺次添加 \(x_2\) 号序列中数字得到的结果，然后删除 \(x_1, x_2\) 对应的序列。

\(q,n\le 5\times 10^5,\sum m\le 5\times 10^5\)

题解

方法

• 主席树+链表

N - 楼房重建

单侧递归线段树

题面

维护一个序列，在线单点修改，求出每一时刻各段的前缀最大值数目。

\(1\le n,m\le 10^5\)

题解

既然是线段树，首先考虑如何合并信息。

如图，黑线两侧是一个节点的左右子树，很明显左子树的答案我们是一定要保留的，对于右子树，我们应该保留那些比黄色的线更高的节点，如果直接用可持久化平衡树维护每个子树中的所有点，一次去 \(\mathcal O(\log)\)的查询自然是可以的，但这样太麻烦。

我们知道，在有序的序列上二分查询比一个数小的复杂度是 \(\mathcal O(\log)\) 的，我们可以用同样的原理，图中红线是将右儿子再次分割，我们可以发现，要么一个孙子全部在黄线上，要么另一个孙子全部在黄线下，我们都只需要递归查找另一个。

这个问题也就是一次上传是 \(\mathcal O(\log)\) 的，这样总复杂度 \(\mathcal O(n\log^2n)\)

方法

• 线段树维护单调序列

  也就是本题的一个套路

• 线段树的 Up 可以看作一个从来是线段树的重中之重，在分析时，我们可以将其看作一个新的问题，这个问题又可以有多种解法，比如说这题，查询黄线上的数，就可以在线段树上再次递归实现，不仅如此，我们可以将其他数据结构、算法等知识运用其上，解决问题。

• 本题也可以使用 T 题的方法达到 \(\mathcal O(n\log n)\)

P - Rikka with Data Structures

题面

给定序列 \(a_{1\sim n}\)

有 \(m\) 次三种类型的操作：

• 区间加
• 区间赋值
• 给定\(l\ r\ x\)：计算满足 \(\max\limits_{i=\min(x,y)}^{\max(x,y)}a_i=max\{A_x,A_y\}\) 的 \(y\) 的数量。

\(多测，1\le T\le 200,1\le n,m\le 10^5,\sum n,\sum m\le 10^6\)

题解

可以注意到 \(y\) 的位置是由若干比 x 小的位置，及第一个比它大的位置后面的前缀和最大值构成的，那个位置可以用“最近元素查找模型”找，后面那一段用单侧递归线段树处理。

复杂度小常数 \(\mathcal O(n\log^2n)\)，最近元素查找模型换成 \(\log^2\) 的二分加线段树会超时。

方法

• 最近元素查找模型

• 单侧递归线段树

S - Bear and Bad Powers of 42

题面

定义一个正整数是坏的，当且仅当它是 \(42\) 的次幂，否则它是好的。

给定一个长度为 \(n\) 的序列 \(a_i\)，保证初始时所有数都是好的。

有 \(q\) 次操作，每次操作有三种可能：

• 1 i 查询 \(a_i\)。
• 2 l r x 将 \(a_{l\dots r}\) 赋值为一个好的数 \(x\)。
• 3 l r x 将 \(a_{l \dots r}\) 都加上 \(x\)，重复这一过程直到所有数都变好。

\(n,q \le 10^5\)，\(a_i,x \le 10^9\)。

题解

T - 前进四

题面

单点修改，询问 \(a_x​,⋯,a_n​\) 的不同的后缀最小值个数。

\(1\le n\le 10^6\)

题解

很明显有一个\(\mathcal O(n\log^2n)\) 的单侧递归线段树做法。但这道题会超时。

如果我们把时间当作空间的一维，那么一个序列上的操作其实是在二维平面上的操作，如图：

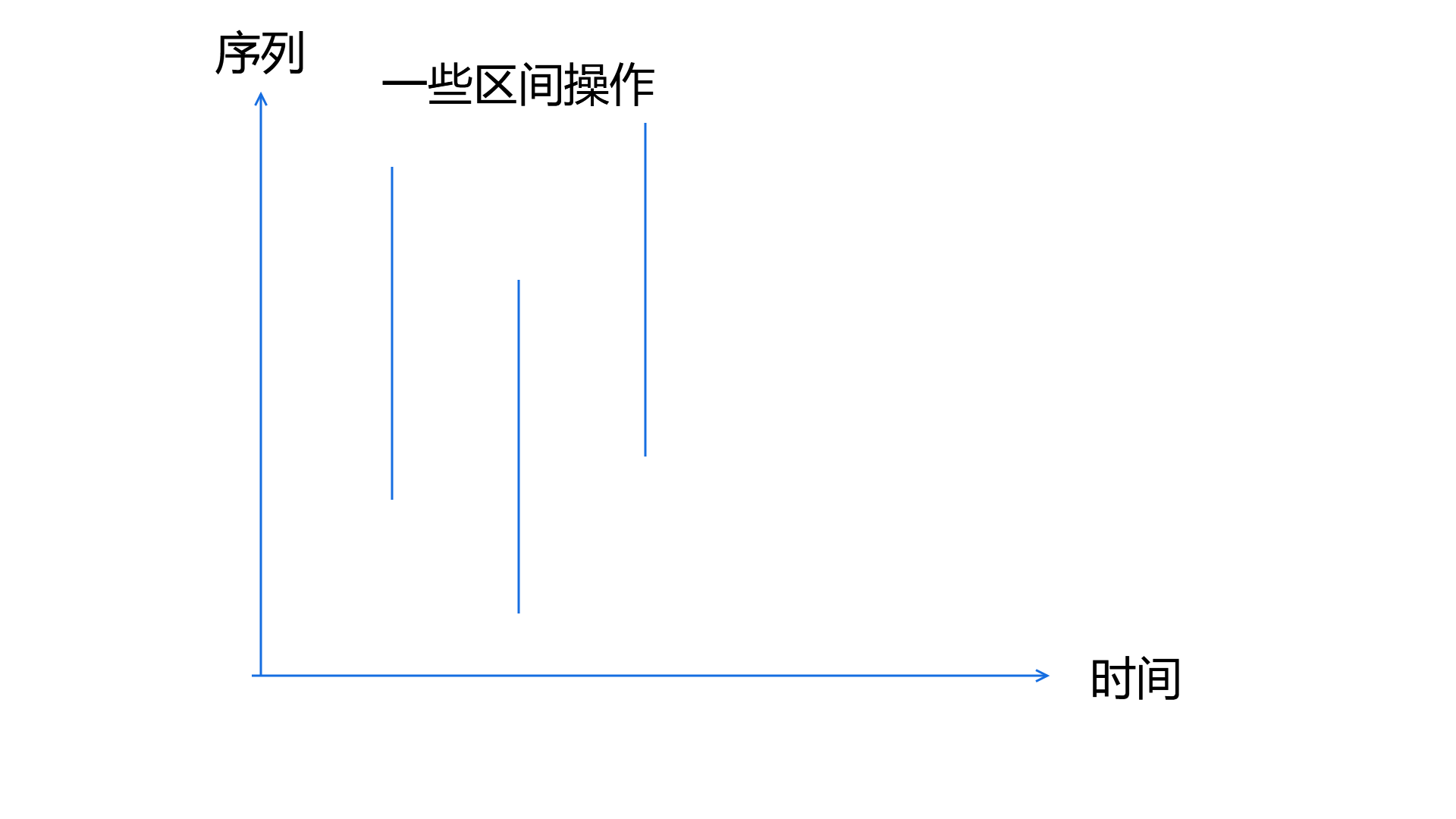
我们在时间轴上进行扫描线，单点修改，维护前缀信息。

而这道题，我们发现查询是一个单点修改，维护后缀信息，然而修改却只在一个时间段有效，所以对于这道题，可以考虑将其转过来。

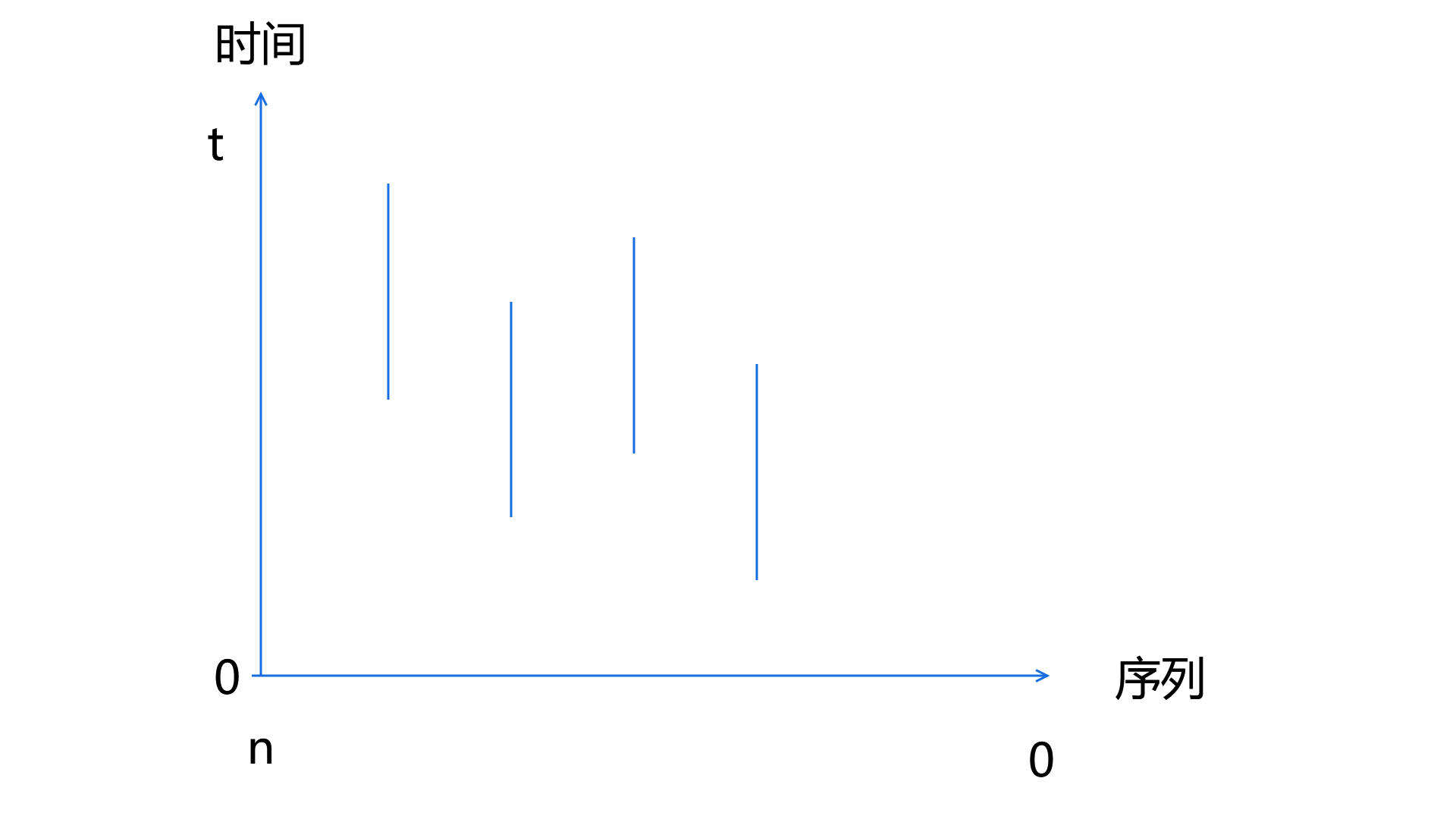
变成一个区间赋最小值，后缀序列扫描线。

方法

• 考虑时间维度