动态规划_李奕辰

动态规划_李奕辰

A - Paint

题面

给你一个颜色序列。每次，你可以把一段颜色相同的段染成另一个颜色。问至少几次才能把所有颜色染成一样的。
\(n ≤ 1000\)，每个颜色最多出现 \(c=20\) 次。

题解

注意到每种颜色的数量很少，从颜色入手

若颜色各不相同，则答案为 \(n-1\)。

如果有两个一样的颜色，那么意为这我们可以少合并一次。

所以设 \(dp[l][r]\) 表示 \([l,r]\) 最多可以少合并多少次。

则 \(dp[l][r]=\max(dp[l][r+1]*,\max_{a_l=a_k,l<k\le r}dp[l+1][k-1]+1+dp[k][r])\)

答案为 \(n-1-dp[1][n]\)，复杂度 \(\mathcal O(cn^2)\)

方法

• 以域小的入手
• 区间 DP 中，通过数学分析尽量少的枚举断点

B - Outer space invaders

题面

有 \(n\) 个外星人，第 \(i\) 个会在 \([a_i,b_i]\) 时间内出现，他的距离为 \(d_i\)。
消灭它至少需要范围为 \(d_i\) 的炸弹。
一个炸弹会消灭此时在的所有能消灭的外星人。问你至少要距离总和多少的炸弹。
\(n\le 300\)

题解

按时间从前往后考虑，方便吗？
很难，因为一个时刻没被消灭的外星人组成了一个单调栈的形状。
能否从值域上入手呢？
先考虑最大的外星人，那么消灭它的时候一定会消灭所有在场的其他外星人。

对时间离散化。
\(f_{i,j}\) 表示要消灭出现时间与消失时间在 \([i,j]\) 之间的所有外星人至少需要多少。当 \(i>j\) 时，\(f_{i,j}=0\)，答案为 \(f_{1,t}\)。
对于 \(f_{i,j}\)，找到完全包含与其中所需威力最大的外星人 \(d\)，设其出现时间为 \([l,r]\) ，则\(f_{i,j}=\min_{l\le k\le r}f_{i,k-1}+w_d+f_{k+1,r}\)

方法

• 以值域入手，考虑最值

C - ρars/ey

题面

给定一颗有 n 个节点的有根树，其中根节点是 1。你可以若干次地选择一个节点，删去其子树内除其以外的点，并伴随有代价为 fi，其中 i 是你选择的节点子树大小。

你希望删掉除了 1 以外的所有点，请问代价的最小值是多少？

\(1\le n\le 5000\)

题解

树形背包的模板题，直接设 \(f_{i,j}\) 表示子树 \(i\) 内删得只剩 \(j\) 个点时最少要多少代价。
答案就是 \(f_{1,1}\)

方法

• 树形背包

EX1 - popcount

题面

给定 \(n,m\) 和 \(a_{1\sim n}\)，请构造值域在 \([0,2^m]\) 的严格单增的数列 \(b_{1\sim n}\)，最大化：\(\sum_{i=1}^na_i\operatorname{popcount}(b_i)\)

其中 \(\operatorname{popcount}(x)\) 表示 \(x\) 在二进制下的为 \(1\) 的位数

\(1\le n\le 500,0\le m\le 30\)

题解

很明显不能存上一个选择的数

由于这道题是求二进制下的情况，我们也可以将数放在二进制下考虑。

考虑所有 \(b\) 的最高位，发现一定是前面是 \(0\)，后面是 \(1\) 。并在每块中考虑第二位，亦是如此，即形如：

111……
110……
101……
100……
011……
010……
001……
000……

于是可以设 \(dp_{i,j,k}\) 表示区间 \([i,j]\) 内小于 \(2^k\) 的方案数，则 \(dp_{i,j,k}=\max_{i\le x< j}dp_{i,x,k-1}+dp_{x+1,r,k-1}+a_j-a_x\) 答案为 \(dp_{1,n,m}\)

方法

• 考虑最值，最值位

EX2 - 拆贡献

题面

给定 \(a_{1\sim n}\) ，求有多少个 \(i,j\) 满足 \((a_i+a_j)(a_i^2+a_j^2)\equiv k\pmod p\)

\(1\le n\le 10^6\)

题解

对于这种有乘法的东西，我们很难做到比枚举 \(i,j\) 更好，能否把 \(i,j\) 分开

\[(a_i-a_j)(a_i+a_j)(a_i^2+a_j^2)\equiv k(a_i-a_j)\pmod p\\ a_i^4-a_j^4\equiv ka_i-ka_j\pmod p\\ a_i^4-ka_i\equiv a_j^4-ka_j\pmod p \]

开个 map 就好了

F - 沈阳大街 2

题面

给定两个长度为 \(n\) 的序列 \(A,B\)，满足：

• \(\forall 1\le i<n,A_i \ge A_{i+1}\)

• \(A_n\ge \min\limits_{i=1}^n(B_i)\)

\(\pi\) 是一个长度为 \(n\) 的排列，定义价值函数 \(f(\pi)\)：

即求:

\[\left(\dfrac{1}{n!}\sum_\pi \prod_{i=1}^n\min(A_i,B_{\pi(i)})\right) \bmod 998244353 \]

\(1\le n\le 5000\)，\(1\le A_i,B_i\le 10^9\)。

解法

P8321 『JROI-4』沈阳大街 2 题解 - 洛谷专栏 (luogu.com.cn)

方法

• 合并考虑

• 匹配

• 排序避免讨论

G - Horrible Cycles

题面

给定一个有\(n\)个顶点的二分图。

在这个图中，左侧部分的每个顶点都连接到右侧部分的一些前缀顶点。换句话说，左侧部分的第\(i\)个顶点与右侧部分的\(1,2,…,a_i\)个顶点相连。

找出这个图中顶点简单环的数量。如果存在某条边在一个环中出现而在另一个环中不存在，则这两个环是不同的。

由于这个数量可能很大，所以要对\(998244353\)取模。

\(1\le n\le 5000\)

题解

因为是一个二分图，一个环一定有相等的左部点与右部点，假设一开始有若干右部点（图中为圆点），考虑不断加入左部点的过程（图中为三角形）。

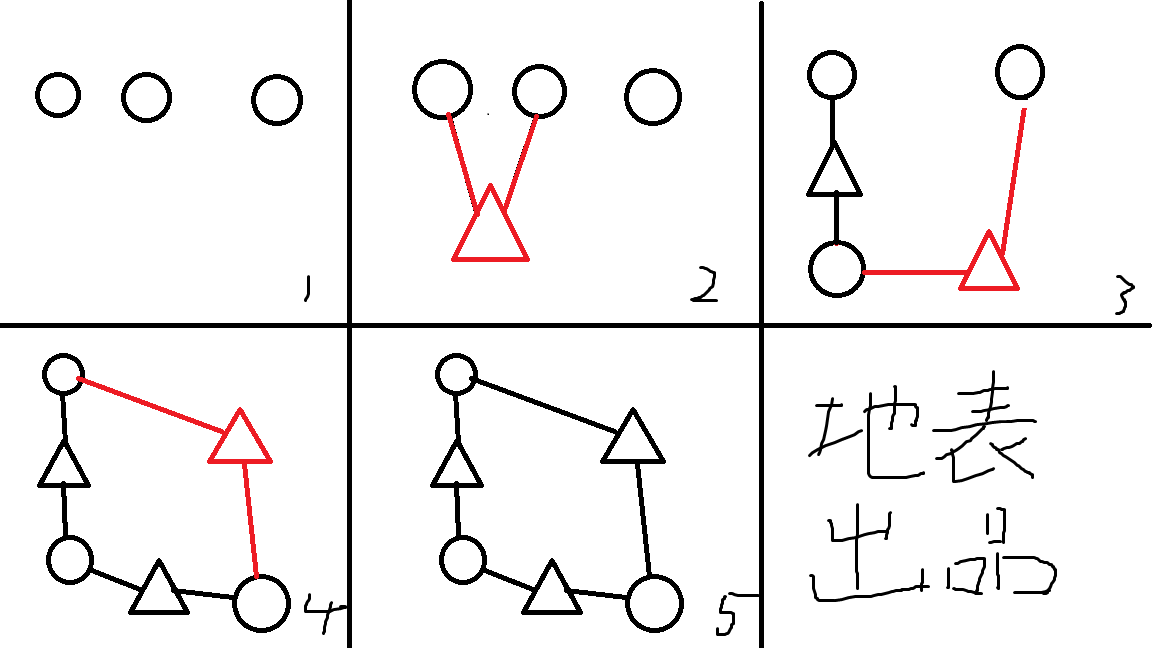
发现考虑一个左部点，就会将链的数量减一直至成为一个环。

于是可以将第 \(i\) 个左部点放在第 \(a_i\) 右部点之后，使得形成一个序列，一个左部点可以与排在他之前的右部点匹配。于是令 \(dp_{i,j}\) 表示对于前 \(i\) 个点，形成 \(j\) 条有向链的方案数，有

\[dp_{i,j}=\left\{\begin{aligned} &dp_{i-1,j-1}+dp_{i-1,j}&&(i为右部点)\\ &(j+1)\times j\times dp_{i-1,j+1}+dp_{i-1,j}&&(i为左部点) \end{aligned}\right. \\ans=\frac{\sum_{i|i是左部点}dp_{i-1,1}-\sum_{i=1}^na_i}{2} \]

注意这个地方必须是“有向链”，因为

是两种方案。

方法

• 在不断增大考虑范围的时候思考结构的成型过程。

  这里的结构可以是比如环一类的结构，然后维护这种变化过程，尝试转移。

• 将两组或者多组数据放在一起，形成一个大序列，考虑整体考虑。

• 匹配思想，在这道题中就是左右点的匹配。

• 有向图形。在考虑一个本身无向的结构的时候，由于链接点的不同或其他原因导致多种情况，可以尝试给这个图形赋予方向，简化解答思路，比如说本题与三维凸包中的“有向面”。

EX3 - Phoenix and Computers

链接

连续段 DP

题面

有一行 \(n\) 台电脑。你可以手动开启一台电脑。当第 \(i-1\) 与 \(i+1\) 台电脑被启动的时候，第 \(i\) 台电脑也会自动启动，已经被选择的不能再次选择，求多少种不同的手动选择的方案，顺序不同视作不同方案，对 \(M\) 取模。

\(3\le n\le 400,10^8\le M\le 10^9\)

题解

考虑使用连续段 DP，\(f_{i,j}\) 表示当有 \(i\) 台电脑被开启，并被合成为的 \(j\) 个连通块的方案数。根据连续段 DP 的套路，按照三种情况讨论。

• 对一个连通块加一个元素，可以隔一个或不隔，有 \(f_{i,j}\leftarrow f_{i-1,j}+f_{i-2,j}\)

• 新增一个连通块，有\(f_{i,j}\leftarrow f_{i-1,j-1}\times j\)

• 合并两个连通块，这两个连通块可以间隔 \(2\) 个或 \(3\) 个，有 \(f_{i,j}\leftarrow f_{i-2,j-1}+f_{i-3,j-1}\)

最后 \(f_{n,1}\) 就是答案

方法

• 连续段 DP/插入 DP/线头 DP

  我们维护的连续段其实并没有放入序列中，其元素的绝对位置是位置的，我们只能通过不断的合并来得知他的绝对位置。也就是说，每一个段看作毫无关系的东西。

  其应从三个角度考虑转移

  • 对一个连通块加一个元素

  • 新建连通块

  • 合并连通块

  线头 dp / 插入 dp / 连续段 dp - 题单

  浅谈一类处理状态转移依赖邻项的排列计数问题的 dp 策略：连续段 dp（线头 dp）

EX4 - Game on Sum

Hard Version、Easy Version

博弈论DP

题面

Alice 和 Bob 正在玩一个游戏，游戏分为 \(n\) 个回合，Alice 和 Bob 要轮流对一个数 x 进行操作，已知这个数初始值是 \(0\)。

具体每个回合的行动规则如下：

1. Alice 选择一个在区间 \([0,k]\) 之间的实数 \(t\)。
2. Bob 可以选择让 \(x\) 变成 \(x+t\) 或者 \(x−t\)，但是 Bob 在 \(n\) 个回合之内至少选择 \(m\) 次让 \(x\) 变成 \(x+t\)。

Alice想让最终的 x 最大，Bob 想让最终的 \(x\) 最小。

已知双方均采用最优策略，求最终的 \(x\) 值（对 \(10^9+7\) 取模）。

数据范围保证：\(1≤m≤n≤2000,k≤10^9+7\)。

题解

CF1628D2 Game on Sum (Hard Version) - 洛谷专栏 (luogu.com.cn)

方法

• 博弈论DP

  因为两人绝顶聪明使得当前决策 仅 基于接下来的决策。

  综上，可以发现一般博弈论的 DP 题都是 从后往前 DP，即从确定的终止状态向初始状态 DP，因为 绝顶聪明 这一条件使得双方都能预测到他们当前的行为对后续局面的影响，可以说只有 后效性 而没有 前效性：若 i,j 确定，则两人之前的决策对当前决策无影响。

EX5 - FLWRS - Flowers

链接

先考虑组合，在乘上阶乘考虑排列

题面

给定 \(N,M\)，求有多少长为 \(N\) 的排列满足相邻元素差的绝对值均不为 \(1\)，答案对 \(M\) 取模。

\(0\le N\le 200,1\le M\le 10^9\)

题解

考虑容斥。

相邻元素差的绝对值均不为 \(1\)，说明 \(i\) 不能与 \(i+1\) 和 \(i-1\) 放在一起。

可以设 \(f_{i,j,0/1}\) 表示考虑值 \(1\sim i\)，其中有 \(j\) 个不满足条件时的带系数组合数，

发现我们可以把每段连续的不合法捆成一个，并伴随升序与降序两种可能。

所以有方程

\[f_{i,j,0}=f_{i-1,j,0}+f_{i-1,j,1}\\ f_{i,j,1}=f_{i-1,j,1}+2f_{i-1,j,0} \]

最后乘上阶乘考虑排列，答案为 \(\sum_{j=0}^n(f_{n,j,0}+f_{n,j,1})\times(n-j)!\)

方法

• 先考虑组合，在考虑排列

EX6 - 题

链接

题面

给定长度为 \(3 n\)、值域为 \([0, 3]\) 的整数序列 \(S = s_1 s_2 \cdots s_{3 n}\)。你需要首先将 \(S\) 中的每个 \(0\) 替换为 \([1, 3]\) 中的任意一个整数，得到序列 \(T = t_1 t_2 \cdots t_{3 n}\)，然后给出 \(n\) 个长度为 \(3\) 的整数序列 \({\{ a_{i, 1}, a_{i, 2}, a_{i, 3} \}}_{1 \le i \le n}\)，使得：

• \(\forall 1 \le i \le n\)，\(1 \le a_{i, 1} < a_{i, 2} < a_{i, 3} \le 3 n\)；
• \(\forall (i_1, j_1) \ne (i_2, j_2)\)，\(a_{i_1, j_1} \ne a_{i_2, j_2}\)；
• \(\forall 1 \le i \le n\)，\(\{ t_{a_{i, 1}}, t_{a_{i, 2}}, t_{a_{i, 3}} \}\) 是 \(\{ 1, 2, 3 \}\) 的一个排列且逆序对数为奇数。

认为两个方案本质不同当且仅当序列 \(T\) 不同或存在 \(a_{i, j}\) 不同，求以上操作的本质不同的方案数，对 \(({10}^9 + 7)\) 取模。

\(1\le n\le 19\)

题解

先得到序列 \(T\)，再使得 \(a_{i,j}\) 不同，可以看作在处理 \(a\) 的过程中，\(S\) 中的 \(0\) 可以当作 \(1，2，3\) 中的任意一个，于是从处理 \(a\) 入手。

易得每个长度为 \(3\) 的整数序列一定是 \(\{1,3,2\},\{2,1,3\},\{3,2,1\}\) 中的一个，考虑成型过程，建立DP。

令 \(dp_{i,a,b,c,d,e,f}\) 表示考虑前 \(i\) 个数时，其中序列为 \(\{1\}\) 的有 \(a\) 个，序列为 \(\{2\}\) 的有 \(b\) 个，序列为 \(\{3\}\) 有 \(c\) 个，序列为 \(\{2,1\}\) 的有 \(d\) 个，序列为 \(\{1,3\}\) 的有 \(e\) 个，序列为 \(\{3,2\}\) 的有 \(f\) 个，的方案数，有：

\[dp_{i,a,b,c,d,e,f}=\left\{\begin{aligned} &dp_{i-1,a-1,b,c,d,e,f}+(b+1)dp_{i-1,a,b+1,c,d-1,e,f}+(f+1)dp_{i-1,a,b,c,d,e,f+1}&&s[i]=1\lor s[i]=0\\ &dp_{i-1,a,b-1,c,d,e,f}+(c+1)dp_{i-1,a,b,c+1,d,e,f-1}+(e+1)dp_{i-1,a,b,c,d,e+1,f} &&s[i]=2\lor s[i]=0\\ &dp_{i-1,a,b,c-1,d,e,f}+(a+1)dp_{i-1,a+1,b,c,d,e-1,f}+(d+1)dp_{i-1,a,b,c,d+1,e,f}&&s[i]=3\lor s[i]=0 \end{aligned}\right. \]

答案即为 \(dp_{3n,0,0,0,0,0,0}\)。

由于 \(a+b+c+d+e+f\le n\) 合法的状态并不多，只有 \(10^5\) 级别，可以通过。

方法

• 考虑答案成型过程，在本题中，就是考虑 ${1,3,2},{2,1,3},{3,2,1} $ 的形成过程，建立 DP。

EX7 - SAO

题面

给定一张有向树形图，求其拓扑序数量。

\(节点数\le 5000\)

题面

如果这些边都是内向边，则由公式 \(\frac {n!}{\prod sz_i}\)，因为每个点应该是其子树内最后一个点，所以会使答案乘上 \(\frac {(sz-1)!}{sz!}=\frac 1{sz}\)。

对于这道题而言，可能会有外向边，于是可以容斥，将外向边转为内向边，设 \(dp_{x,i}\) 表示原树以 \(x\) 为根的子树中，构成了大小为 \(i\) 的内向树的带容斥系数方案数。有：

\[\begin{aligned} &dp_{x,i+j}'\leftarrow dp_{x,i}\times dp_{y,j}\times {siz_{x}+siz_{y}\choose siz_{y}}&&(x,y) 为内向边\\ &dp_{x,i+j}'\leftarrow -dp_{x,i}\times dp_{y,j}\times {siz_{x}+siz_{y}\choose siz_{y}}&&(x,y) 为外向边,表示钦定此边\\ &dp_{x,i}\leftarrow dp_{x,i}\times dp_{y,j}\times {siz_{x}+siz_{y}\choose siz_{y}}&&(x,y) 为外向边，表示不钦定此边 \end{aligned} \]

最后 \(dp_{x,i}\leftarrow \frac {dp_{x,i}}{siz_x},\sum_idp_{0,i}\) 为答案

方法

• 利用容斥将同时出现两种相反的限制的情况变为一种限制

EX8 - 小 N 的独立集

DP套DP

题面

给定 \(n\) 个点的树的形态以及点的权值范围 \([1,k]\)，对于任意 \(i∈[1,kn]\)， 求有多少种权值分配方案，使得树的最大权独立集大小为 \(i\)。

\(1\le n\le 10^3,1\le k\le 5\)

题解

P8352 SDOI2022 D2T1 小 N 的独立集 题解 - 洛谷专栏 (luogu.com.cn)

方法

• DP套DP，将一个简单DP的值设作一个复杂的DP状态，其状态转移就是小 DP 的值的状态转移方程

EX9 - 梦幻岛宝珠

题面

给你 \(n\) 颗宝石，每颗宝石都有重量和价值。要你从这些宝石中选取一些宝石，保证总重量不超过 \(W\)，且总价值最大，并输出最大的总价值。

\(1\le n \le 100\)，\(1\le W,w_i,v_i \le 2^{30}\)。
保证每个 \(w_i\) 能写成 \(a \times 2^b\space (a,b \in \mathbb N)\) 的形式，\(a \leq 10\) , \(b \leq 30\)，且答案不超过 \(2^{30}\)。

题解

将 \(W\) 放在二进制下考虑，状态中只保存会变化的值。

方法

• 欲得到 \(f_x\) 然而 \(x\) 十分的大，当转移的物品的限制的有效位很少时，不存储那些固定位置的信息。

EX10 - Rotation Sort

题面

给定一个排列。
你可以花 \(A\) 的代价把一个数往左移任意距离；花 \(B\) 的代价把一个数往右移任意距离。
要把整个排列排序至少需要多少代价。

\(n\le 5000\)

题解

分析过程可知，答案一定为一个上升序列不动，其他数左右移动，于是令 \(dp_{i}\) 表示考虑前 \(i\) 个数，让以 \(i\) 结尾的上升子序列不动，其余数移动的方案数，则有：

\[dp_{i}=\min_{j<i}dp_j+res_{j+1,i-1} \]

其中 \(res_{i,j}\) 表示将 \([i,j]\) 中的数移动至两边的权值，令 \(res_{0,i,j}\) 表示区间 \([i,j]\) 不得不向左移的数的数量，\(res_{1,i,j}\) 表示区间 \([i,j]\) 中不得不向右移的数的数量，有：

\[\begin{aligned} &res_{0,i,j}=res_{0,i,j-1}+[a_j<a_{i-1}]\\ &res_{1,i,j}=res_{1,i-1,j}+[a_i<a_{j+1}]\\ &res_{i,j}=res_{0,i,j}\times B+res_{1,i,j}\times A+(j-i+1-res_{0,i,j}-res_{1,i,j})\times \min(A,B) \end{aligned} \]

于是 \(\mathcal O(n^2)\) 可解

方法

• 考虑确定状态，即一种方案下的答案情况，接着对方案的状态进行 DP 转移。

EX11 - Make Equal

题面

给出序列 \(a_{1\sim n}\)​ ，每次操作可以给其中一个数加上 \(2\) 的非负整数次幂。求最少的操作次数，使得这 \(n\) 个数相等。

\(1\le n\le 10^5,0\le a_i\le 10^{17}\)

题解

题目可转化为求 \(\min_{x\ge \max a}\sum_{i=1}^n\operatorname{popcount}(x-a_i)\)

令 \(a_i\leftarrow \max a-a_i\)

可化为 \(\min_{x\in \N},\sum_{i=1}^n\operatorname{popcount}(x+a_i)\)

可以发现主要时难以处理进位，因为 \(x+a_i\) 在二进制第 \(i\) 位进位的充要条件为 \(x\bmod 2^i+a_i\bmod 2^i\ge 2^i\) 所以可以按照 \(a_i\bmod 2^i\) 从大到小排序，令 \(dp_{bit,i}\) 表示从小到大考虑到第 \(bit\) 为时，前 \(i\) 个数进位的最小操作次数，决策为 \(x\) 在这一位上是 \(0/1\) 转移即可。复杂度 \(\mathcal O(n\log n\log a)\)，用基数排序可以优化至 \(\mathcal O(n\log a)\)。

方法

• 排序+贪心

• 如果有 \(x\ge \max a\) 转化为 \(y=x-\max a\ge 0\) 进行处理，可以起到划归简化的效果