树形DP个人总结
树形DP
华中农业大学 Linear_L
一、简介
关于 $ dp $ ,我们回顾其具有的两条性质:$ 1. $ 重叠子问题 $ 2. $ 最优子结构
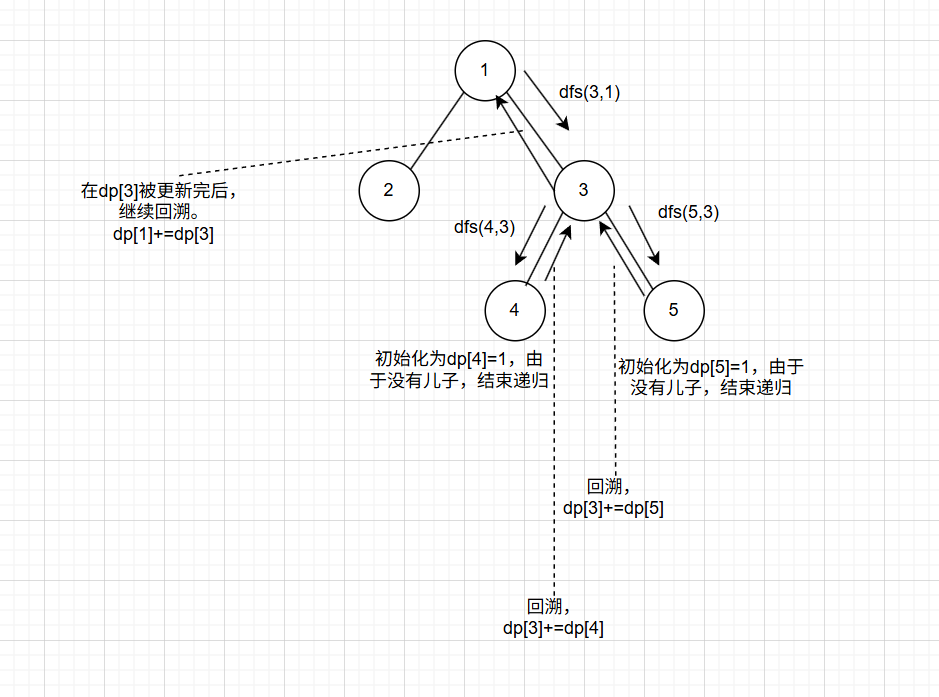
而对于将树这种数据结构与之联系,我们会发现树本身就具有“子结构”的性质(即树与子树),是具有递归性质的。所以我们可以很自然的想如果要维护一颗树的信息,那么我们可以将其转化为维护若干个子树的信息,并用子树的信息去更新根的信息,因此就诞生了树形 $ dp $ 。树形 $ dp $ 通常要将树转化为有根树,然后在树上做 $ DFS $ ,递归到最底层的叶子节点,然后一层层返回更新父亲节点、直至根节点。
二、例题
1. 子树大小问题
给你一颗有 $ n $ 个点的树($ 1 $ 号点为根节点),求以 $ i $ 为根的子树大小。
我们会不妨记 $ dp_i $ 为以 $ i $ 为根的子树大小,那么我们会很容易得到以下转移方程:
式中 $ son_u $ 表示节点 $ u $ 的儿子集合。
代码:
void dfs(int u,int fa)//参数传入当前节点u,以及其父亲fa
{
dp[u]=1;//首先,以u为根的子树肯定包含自己,即初始化为1
for(auto v:edge[u])//遍历u的儿子
{
if(v==fa) continue;//由于在建树的过程中建的是双向边,所以会遍历到自己的父亲
dfs(v,u);//先递归,再更新。
dp[u]+=dp[v];//用子树信息来更新
}
}
我们来解释一下这个想法,以便后续更好的理解树形 $ dp $ 。
代码中可能唯一比较难以理解的是“先递归,再更新”,我们不妨假设如果将 dfs(v,u) 与 dp[u]+=dp[v] 两句交换顺序会发生什么。
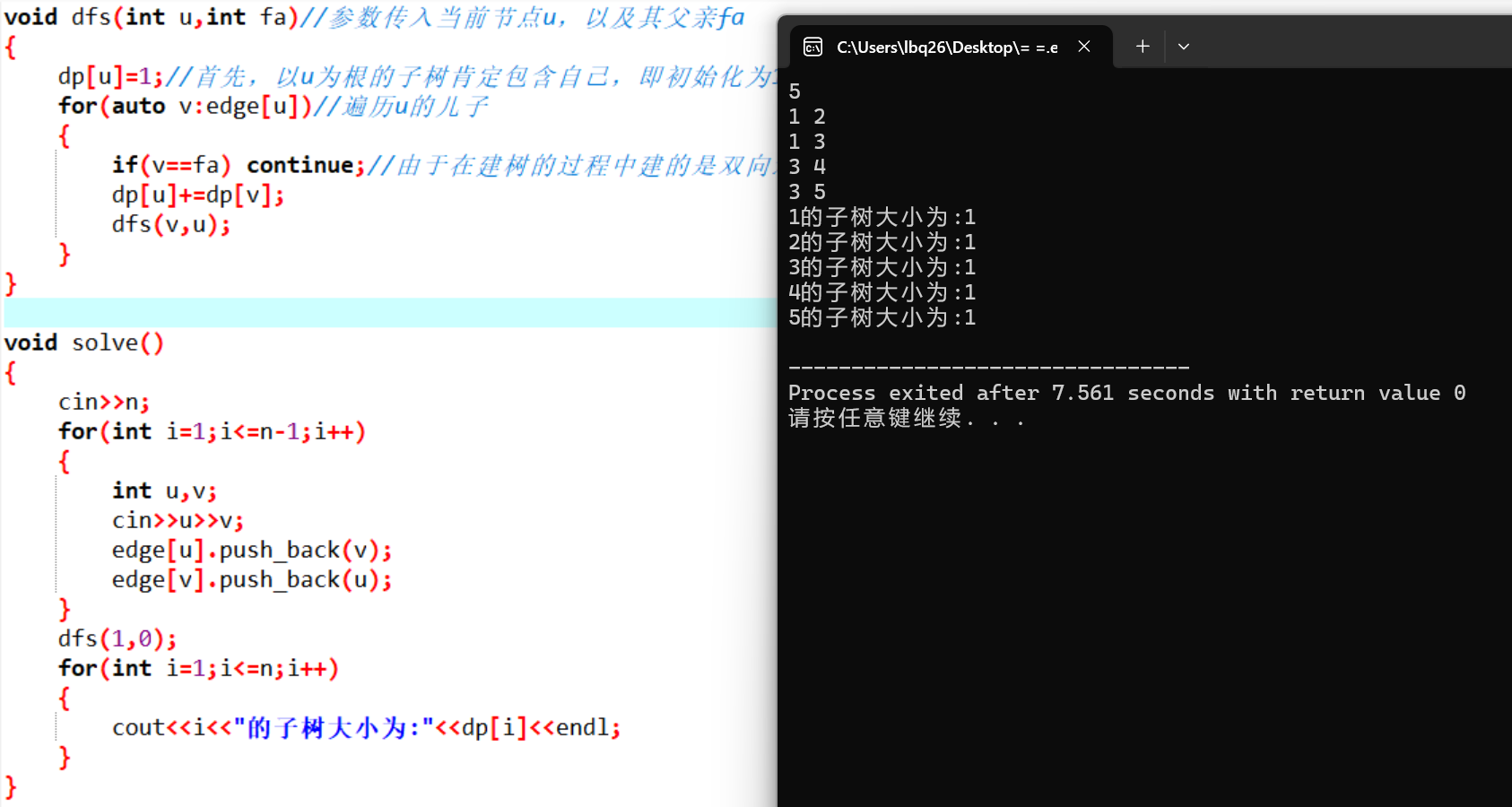
会发现每个节点的子树大小都为初始化的 $ 1 $ ,证明并没有发生“用子树来更新根节点”这个效果。为什么呢?因为在dfs(v,u)一句中其实是先更新子树节点的信息的过程。如果子树信息都没有被更新,那么根节点又如何用子树信息来更新呢?
完整代码及样例图:
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int maxn=2e5+10;
int n,dp[maxn];
vector<int>edge[maxn];
void dfs(int u,int fa)//参数传入当前节点u,以及其父亲fa
{
dp[u]=1;//首先,以u为根的子树肯定包含自己,即初始化为1
for(auto v:edge[u])//遍历u的儿子
{
if(v==fa) continue;//由于在建树的过程中建的是双向边,所以会遍历到自己的父亲
dfs(v,u);//先递归,再更新。
dp[u]+=dp[v];//用子树信息来更新
}
}
void solve()
{
cin>>n;
for(int i=1;i<=n-1;i++)
{
int u,v;
cin>>u>>v;
edge[u].push_back(v);
edge[v].push_back(u);
}
dfs(1,0);
for(int i=1;i<=n;i++)
{
cout<<i<<"的子树大小为:"<<dp[i]<<endl;
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
// cin>>t;
while(t--)
{
solve();
}
return 0;
}
2. 树的最大权独立集
题目链接:洛谷P1352 没有上司的舞会
题意:
给你一颗有 $ n $ 个点的树,每个点都有一个点权,你需要从中选取若干个点,使得它们的点权和最大且要求选取的若干点中任意两个点不会有连边。(树的最大权独立集)
思路:
关于此类问题,我们通常设状态 $ dp[u][0/1] $ 表示对于节点 $ u $ 、考虑其不选/选,能从以 $ u $ 为根节点的子树中获得的最大权独立集。我们只思考以节点 $ u $ 为根的子树,对于节点 $ u $ 的选与不选只会决定于它的儿子 $ v \in son_u $ 的能否选取。那么我们有如下转移:
式中 $ a[u] $ 代表 $ u $ 的点权。我们对转移方程详细解释一下:
- $ dp[u][0] $ 表示不选择当前节点 $ u $ ,那么它的子节点可选也可以不选,我们取其中的最大值添加即可。
- $ dp[u][1] $ 表示选择当前节点 $ u $ ,那么它的子节点一定不能选,即:
最后的答案我们只需要在 $ dp[1][0],dp[1][1] $ 中取最大值即可(默认根节点为 $ 1$)。
代码:
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int maxn=2e5+10;
int n,dp[maxn][2],a[maxn];
vector<int>ds[maxn];
void dfs(int u,int fa)
{
dp[u][1]=a[u];
for(auto v:ds[u])
{
if(v==fa) continue;
dfs(v,u);
dp[u][0]+=max(dp[v][0],dp[v][1]);
dp[u][1]+=dp[v][0];
}
}
void solve()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n-1;i++)
{
int u,v;
cin>>u>>v;
ds[u].push_back(v);
ds[v].push_back(u);
}
dfs(1,0);
cout<<max(dp[1][0],dp[1][1])<<endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
// cin>>t;
while(t--)
{
solve();
}
return 0;
}
3. 树的最小点覆盖
题目链接:洛谷P2016 战略游戏
题意:
给你一颗有 $ n $ 个点的树,如果在一个节点上放置一位士兵,那么该节点所连的所有边都会被看守,问你至少需要放置多少个士兵,使得这颗树上所有边被看守。
思路:
我们发现这道题与最大权独立集十分相似,只不过唯一不同的是父亲和儿子可以同时选。我们依旧设计状态 $ dp[u][0/1] $ 代表不在/在节点 $ u $ 上放置士兵并且以 $ u $ 为根的每条边都会被看守的最小士兵数。
下面考虑转移:
下面详细解释一下转移方程的含义:
- $ dp[u][0] $ 表示节点 $ u $ 不放置士兵时,以 $ u $ 为根节点的子树的所有边都被看守的最少士兵数。当节点 $ u $ 不放置士兵时,那么它的所有儿子就必须要放置士兵,否则节点 $ u $ 与其儿子的连边就不会被看守。
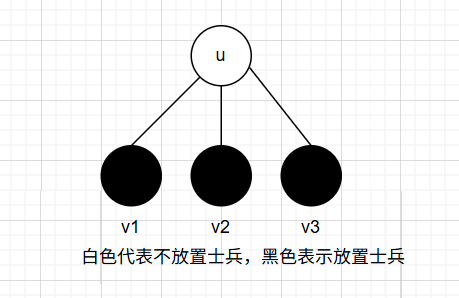
- $ dp[u][1] $ 表示节点 $ u $ 放置士兵时,以 $ u $ 为根节点的子树的所有边都被看守的最少士兵数。当节点 $ u $ 放置士兵时,那么它的所有儿子可以选择放也可以不选择放置士兵,因为它们与父亲的连边已经被父亲所放置的士兵给看守了。
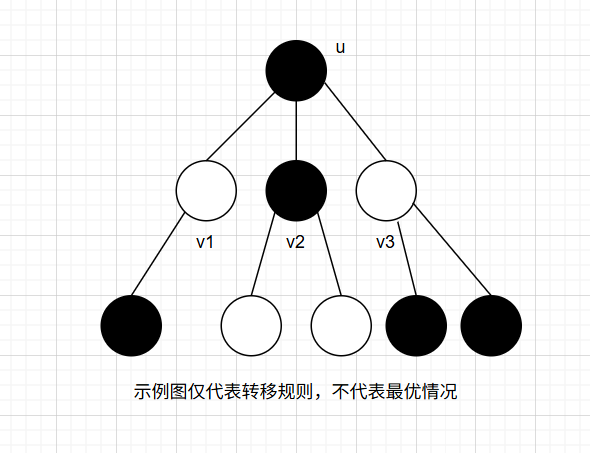
最后的答案即为:$ \min(dp[root][0],dp[root][1]) $
代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=20010;
int dp[maxn][2];
vector<int>ds[maxn];
void dfs(int u,int fa)
{
dp[u][0]=0;
dp[u][1]=1;
for(int i=0;i<ds[u].size();i++)
{
int v=ds[u][i];
if(v==fa) continue;
dfs(v,u);
dp[u][1]+=min(dp[v][0],dp[v][1]);
dp[u][0]+=dp[v][1];
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int id;
cin>>id;
int k;
cin>>k;
for(int j=1;j<=k;j++)
{
int v;
cin>>v;
ds[id].push_back(v);
ds[v].push_back(id);
}
}
dfs(0,-1);
cout<<min(dp[0][0],dp[0][1])<<endl;
return 0;
}
4. 树的最小支配集
题目链接:洛谷P2458 保安站岗
题意:
有一颗点带有点权的树,如果选择一个点安置保安,那么保安会支配与该节点相连的所有点(包括自己),求能让所有节点全部被支配的最小代价。
思路:
我们首先要将树的最小支配集和最小点覆盖区分开来,显然前者是全部点都要求覆盖,而后者是全部边要求覆盖。
我们先尝试用最大独立集的思想去解决此题,我们设 $ dp[u][0/1] $ 为第 $ u $ 个点不放置/放置保安、以 $ u $ 为根节点的子树全部点都被支配所需要的最小花费。考虑转移:
会发现错完了,我们会发现当第 $ u $ 个点不放置保安时,其儿子只需要一个选择放置保安就可以支配到该节点,同时,我们也没有考虑到节点 $ u $ 的父亲对其的支配与否。
也就是说,每个点都可能由自己、父亲、儿子三种可能来支配。
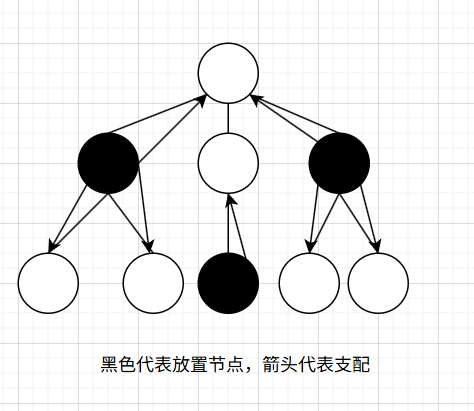
我们考虑增加状态,不妨设:
- $ dp[u][0] $ 表示节点 $ u $ 由自己支配、以节点 $ u $ 作为根的子树内的点全部被看管的最小代价。
- $ dp[u][1] $ 表示节点 $ u $ 由父亲支配、以节点 $ u $ 作为根的子树内的点全部被看管的最小代价。
- $ dp[u][2] $ 表示节点 $ u $ 由儿子支配、以节点 $ u $ 作为根的子树内的点全部被看管的最小代价。
下面分开解释如何转移:
-
节点 $ u $ 由自己支配
即安置一名保安于节点 $ u $ ,会发现带来的效应是节点 $ u $ 的父亲和全部儿子都会被支配。那么儿子可以选择任意一种状态来进行转移。
\[dp[u][0]=a[u]+\sum\limits_{v \in son_u} \min(dp[v][0],dp[v][1],dp[v][2]) \] -
节点 $ u $ 由父亲支配
即不会安置一名保安于节点 $ u $ ,那么自己的儿子只会被自己支配或者是由其儿子给支配。则有:
\[dp[u][1]=\sum\limits_{v \in son_u} \min(dp[v][0],dp[v][2]) \] -
节点 $ u $ 由儿子支配
同样的,节点 $ u $ 依旧不会放置一名保安,那么儿子也只会有两种状态:(1)由自己支配 (2)由自己的儿子支配。可以得到转移方程:
\[dp[u][2]=\sum\limits_{v \in son_u} \min(dp[v][0],dp[v][2]) \]
但是考虑一个问题,如果节点 $ u $ 所有的儿子都选择由其对应的儿子支配,无一人选择自己支配自己,那么节点 $ u $ 就会处于无人支配的状态。具体的,当所有的 $ \min(dp[v][0],dp[v][2])(v \in son_u) $ 都返回的是 $ dp[v][2] $ ,那么节点 $ u $ 就会无人支配。为了解决此问题,我们就可以在转移的时候加一个特判即可。
代码:
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
using i64=long long;
using i128=__int128;
template<class G> inline void read(G& x)
{
bool f; char ch = getchar();
for (f = 0; !isdigit(ch); ch = getchar())if (ch == '-')f = 1;
for (x = 0; isdigit(ch); x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar());
x *= f == 1 ? -1 : 1;
}
void write(i128 x)
{
if(x<0)
putchar('-'),x=-x;
if(x>9)
write(x/10);
putchar(x%10+'0');
return;
}
const i64 INF=1e16; //判断状态无解的情况
const int maxn=2e3+10;
vector<int>ds[maxn];
i64 dp[maxn][3],a[maxn];
bool vis[maxn];
//0:自己支配自己
//1:父亲支配自己
//2:儿子支配自己
void dfs(int u,int fa)
{
dp[u][0]=a[u];
int g[maxn];
int cnt=0;
for(auto v:ds[u])
{
if(v==fa) continue;
dfs(v,u);
dp[u][0]+=min({dp[v][0],dp[v][1],dp[v][2]});//由自己支配自己
dp[u][1]+=min(dp[v][0],dp[v][2]);//由父亲支配自己
//由儿子支配自己
dp[u][2]+=dp[v][0];//先默认所有的儿子全部都放置一名保安
g[++cnt]=dp[v][2]-dp[v][0];//g数组存放当前节点的儿子的两种支配方式的差距
}
sort(g+1,g+1+cnt);
if(cnt==0) dp[u][2]=INF;//如果当前节点u为叶子节点,就不可能由儿子来支配自己
for(int i=1;i<cnt;i++)//注意这里的 i < cnt,思考为什么不能取等
{
if(g[i]<0) dp[u][2]+=g[i];
else break;
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
int u,m,v;
cin>>u;
cin>>a[u]>>m;
for(int j=1;j<=m;j++)
{
cin>>v;
ds[u].push_back(v);
ds[v].push_back(u);
}
}
dfs(1,0);
cout<<min(dp[1][0],dp[1][2])<<endl;
return 0;
}
5. 树上背包
题目链接:洛谷 P2014 选课
题意:
给一颗有 $ n $ 个节点的有根树,第 $ i $ 个节点 的价值为 $ w_i $ ,体积为 $ v_i $ 。现在背包容量为 $ m $ ,如果当前节点 $ u $ 被选,那么其所有祖先都必须被选,问如何选择可以使得物品总价值最大。
思路:
我们定义泛化物品为没有固定的费用和价值,且费用与价值成函数关系的物品。泛化物品用一个一维数组 $ dp $ 进行表示,其中 $ dp[i] $ 表示该泛化物品在费用为 $ i $ 时的价值。那么两个泛化物品 $ dp_1,dp_2$ 在价值尽可能大的情况下合并为一个泛化物品,有:
显然时间复杂度是 $ O(m^2) $ 的。
那么我们可以将每个子树都视为一个泛化物品,令 $ dp[i][j] $ 表示以 $ i $ 为根的子树中,选出体积不超过 $ j $ 的物品
组合的最大价值,也就是以 $ i $ 为根的子树构成一个泛化物品,在不超过 $ k $ 的容量下的最大价值。开始未合并其子树时,其代价为 $ dp[i][j]=w_i,j \geq v_i $ 。
根据上文提及,不难看出有如下转移方程:
代码:
时间复杂度: $ O(nm^2) $
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int maxn=500;
int n,m,dp[maxn][maxn],a[maxn];
vector<int>ds[maxn];
void dfs(int u,int V)
{
for(int i=1;i<=V;i++) dp[u][i]=a[u];
for(auto v:ds[u])
{
dfs(v,V-1);
for(int j=V;j>=1;j--)
for(int k=0;k<=j-1;k++)
dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[v][k]);
}
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int fa;
cin>>fa>>a[i];
ds[fa].push_back(i);
}
dfs(0,m+1);
cout<<dp[0][m+1]<<endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int t=1;
// cin>>t;
while(t--)
{
solve();
}
return 0;
}
考虑优化,我们发现在遍历当前的节点 $ u $ 的每个儿子时,都会重新跑一遍整个背包的容量 $ V $ ,也即是循环:
for(int j=V;j>=1;j--)
表示当前以 $ u $ 作为根节点的子树(包括根节点 $ u $ 以及已经遍历了的儿子 $ v $ 的子树,并不是根节点 $ u $ 的全部子树,该值会在遍历的过程中逐步累加)选择了 $ j $ 个点。会发现当前子树大小(不妨记为 $ sz[u] $)很小时,会有大部分状态都会被浪费,因为即使将当前子树的全部点全部选完都不会到达 $ V $ 。所以我们考虑上下界优化,相关代码如下:
void dfs(int u,int V)
{
for(int i=1;i<=V;i++) dp[u][i]=a[u];
sz[u]=1;
for(auto v:ds[u])
{
dfs(v,V-1);
for(int j=min(sz[u]+sz[v],V);j>=1;j--)
{
//j>sz[u]+sz[v]就没有任何意义,根本不会到达这种情况
for(int k=max(0ll,j-sz[u]);k<=min(j-1,sz[v]);k++)
{
//以v作为根的子树最多会选sz[v]个点,同时在保证根节点被选的情况下,最多选j-1个
//k最少会选择j-sz[u]个
dp[u][j]=max(dp[u][j],dp[u][j-k]+dp[v][k]);
}
}
sz[u]+=sz[v];//这里以u作为根的子树大小是实时更新的(边遍历边更新)
}
}
时间复杂度可以证明是 $ O(nm) $ 的,证明如下:
不妨令 $ sum_{i,j} $ 表示以 $ i $ 为根的前 $ j $ 个儿子的子树大小,$ son_{i,j} $ 表示以 $ i $ 作为父亲的第 $ j $ 个儿子,$ sz_i $ 表示以 $ i $ 为根的子树大小,$ num_i $ 表示节点 $ i $ 的儿子个数。
我们对于第 $ i $ 个节点,每做一次合并时间复杂度都是$ O(sum_{i,j-1}\times sz_{son_{i,j}}) $ ,则总体时间复杂度有:
考虑对于节点 $ i $,我们会发现当 $ i $不作为根节点时,会贡献一次 $ sz_i^2 $ 以及一次 $ sz_{son_{i,j}}^2 $ ,两次贡献相互抵消,因此最后的时间复杂度为:$ O(sz_{root}^2) $ = $ O(n^2) $ ,通常情况下子树合并的上界是给定的 $ m $,故不难证明时间复杂度为 $ O(nm) $ ,证毕。
除此之外,树上背包上下界优化时间复杂度证明还存在势能分析法,考虑不是本文重点,仅提供学习的链接:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号