Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

Proceedings of the 36th International Conference on Machine Learning, PMLR 97:5331-5340, 2019

 

Abstract

　　深度强化学习算法需要大量的经验来学习单个任务。虽然元强化学习（meta-RL）算法可以使智能体从少量经验中学习新技能，但有几个主要挑战阻碍了它们的实用性。目前的方法在很大程度上依赖于同策经验，限制了它们的样本效率。他们在适应新任务时也缺乏推理任务不确定性的机制，这限制了他们在稀疏奖励问题上的有效性。在本文中，我们通过开发一种异策元RL算法来解决这些挑战，该算法将任务推理和控制解耦。在我们的方法中，我们对潜在任务变量进行在线概率过滤，以根据少量经验推断如何解决新任务。这种概率解释使后验采样能够用于结构化且高效的探索。我们展示了如何将这些任务变量与异策RL算法集成，以实现元训练和自适应效率。我们的方法在采样效率以及在几个元RL基准上的渐近性能方面优于现有算法20-100倍。

 

1. Introduction

　　强化学习（RL）与强大的非线性函数近似器的结合导致了序列决策问题的广泛进展。然而，传统的RL方法为每个任务学习一个单独的策略，每个策略通常需要与环境进行数百万次交互。用这种方法学习大量的行为很快就会变得令人望而却步。

　　幸运的是，我们希望自主智能体解决的许多问题都有共同的结构。例如，在瓶子上拧盖子和转动门把手都需要抓住手中的物体并转动手腕。利用这种结构更快地学习新任务仍然是一个开放而紧迫的话题。元学习方法通过利用在任务分布中收集的大量经验，从经验中学习这种结构。一旦学会，只要有少量的经验，这些方法就能快速适应新任务。

　　虽然元学习策略只需几次试验就可以适应新任务，但在训练过程中，它们需要从大量不同的任务中提取大量数据，这加剧了困扰RL算法的样本效率问题。大多数当前的元RL方法在元训练和适应过程中都需要同策数据（Finn et al.，2017；Wang et al.，2016；Duan et al.，2016；Mishra et al.，2018；Rothfuss et al.，2018；Houthoft et al.，2018），这使得它们在元训练过程中效率极低。然而，将异策数据用于元RL带来了新的挑战。使用异策数据对策略进行元训练以适应本质上是困难的，因为这些数据与策略在元测试时在新任务中探索（同策）时看到的数据系统性地不同。此外，与异策算法相比，同策方法可以在元训练期间学习探索对策，因为它们直接控制适应数据分布（Duan et al.，2016；Rothfuss et al.，2018）。如果没有这种控制，异策元学习方法必须采用额外的机制来实现有效的探索。

　　在本文中，我们解决了有效的异策元强化学习问题。为了实现元训练效率和快速自适应，我们提出了一种将概率上下文变量的在线推理与现有的异策RL算法相结合的方法。快速适应需要对分布进行推理：当第一次接触到新任务时，最优元学习策略必须执行随机探索程序，以访问潜在的奖励状态，并适应手头的任务（Gupta et al.，2018）。在元训练过程中，我们学习了一个概率编码器，该编码器将过去经验中的必要统计信息累积到上下文变量中，使策略能够执行任务。在元测试时，当智能体面临一个看不见的任务时，可以对上下文变量进行采样，并在一段时间内保持不变，从而实现时间上的扩展探索。收集的轨迹用于更新上下文变量上的后验，实现快速的轨迹级自适应。实际上，我们的方法通过对“任务假设”进行抽样，尝试这些任务，然后评估这些假设是否正确来进行调整。将任务推理从动作中分离出来，可以最大限度地减少元训练和元测试之间的分布不匹配；策略可以用异策数据进行优化，而概率编码器则用策略数据进行训练。

　　我们工作的主要贡献是一种异策元RL算法，Actor-Critic元RL的概率嵌入（PEARL）。我们的方法在元训练中实现了出色的样本效率，通过在线积累经验实现了快速适应，并通过对任务的不确定性进行推理来进行结构化探索。在我们的实验评估中，我们展示了最先进的结果，在六个连续控制元学习域上，元训练样本效率提高了20-100倍，渐近性能显著提高。我们研究了我们的模型如何在回报稀疏的二维导航环境中进行结构化探索，以快速适应新任务。我们的PEARL开源实现可以在https://github.com/katerakelly/oyster.

 

2. Related Work

Meta-learning. 我们的工作建立在元学习框架的基础上（Schmidhuber，1987；Bengio et al.，1990；Thrun & Pratt，1998）。最近，元学习动力学模型（Nagabandi et al.，2019；Sæmundsson et al.，2018；Doshi-Velez & Konidaris，2016）和能够适应新任务的策略（Finn et al.，2017；Duan et al.，2016；Mishra et al.，2018）已经开发了元RL方法。

　　循环（Duan et al.，2016；Wang et al.，2016）和递归（Mishra et al.，2018）元RL方法通过将经验聚合为策略所依赖的潜在表示来适应新任务。这些方法可以归类为我们称之为基于上下文的元RL方法，因为神经网络被训练为将经验作为输入，作为特定任务上下文的一种形式。同样，我们的方法也可以被认为是基于上下文的；然而，我们用概率潜在变量来表示任务上下文，从而能够对任务的不确定性进行推理。我们没有使用递归，而是利用置换不变编码器中的马尔可夫特性来聚合经验，从而实现快速优化，尤其是对于长期任务，同时减少过拟合。虽然先前的工作已经研究了可以使用异策Q学习方法训练递归Q函数的方法，但这种方法通常应用于更简单的任务（Heess et al.，2015）和离散环境（Hausknecht & Stone，2015）。事实上，我们自己在第6.3节中的实验表明，将循环策略与异策学习直接结合起来是困难的。情境方法也被应用于模仿学习，方法是按照演示学到的嵌入调整策略，并通过行为克隆进行优化（Duan et al.，2017；James et al.，2018）。

　　与基于上下文的方法相比，基于梯度的元RL方法使用策略梯度从聚合经验中学习（Finn et al.，2017；Stadie et al.，2018；Rothfus et al.，2018；Xu et al.，2018a）、元学习损失函数（Sung et al.，2017；Houthooft et al.，2018）或超参数（Xu et al.，2018b）。这些方法侧重于同策元学习。相反，我们专注于从异策数据中进行元学习，这与基于策略梯度和进化优化算法的方法无关。除了大幅提高样本效率外，我们还从经验上发现，与使用策略梯度的方法相比，我们基于上下文的方法能够达到更高的渐近性能。

　　在RL之外，针对小样本监督学习问题的元学习方法已经探索了各种各样的方法和架构（Santoro et al.，2016；Vinyals et al.，2016；Ravi & Larochelle，2017；Oreshkin et al.，2018）。我们的置换不变嵌入函数受到原型网络嵌入函数的启发（Snell et al.，2017）。虽然他们在学到的确定性嵌入空间中使用距离度量来对新输入进行分类，但我们的嵌入是概率性的，用于调节RL智能体的行为。据我们所知，之前没有任何工作提出这种特殊的元RL嵌入函数。

Probabilistic meta-learning. 先前的工作已经将概率模型应用于监督和RL领域的元学习。分层贝叶斯模型已被用于建模小样本学习（Fei-Fei et al.，2003；Tenenbaum，1999），包括执行基于梯度的自适应的方法（Grant et al.，2018；Yoon et al.，2018）。关于监督学习，Rusu等人(2019)；Gordon等人(2019)；Finn等人(2018)使用通过摊销近似推理推断出的概率潜在任务变量来调整模型预测。我们将这个想法扩展到异策元RL。在多任务RL的背景下，Hausman等人(2018)根据推断的任务变量来调整策略，但其目的是通过嵌入空间来组合任务，同时我们专注于快速适应新任务。当我们推断任务变量并通过后验采样进行探索时，MAESN（Gupta et al.，2018）通过梯度下降优化任务变量进行调整，并通过从先验采样进行探索。

Posterior sampling. 在经典RL中，后验采样（Strens，2000；Osband et al.，2013）在可能的MDP上保持后验，并通过根据采样的MDP进行最佳操作来实现时间扩展的探索。我们的方法可以被解释为该方法的元学习变体：概率上下文捕获任务的当前不确定性，允许自媒体以类似的结构化方式在新任务中进行探索。

Partially observed MDPs. 元RL中测试时的适应可以被视为POMDP中RL的一种特殊情况（Kaelbling et al.，1998），因为它将任务作为状态中未观察到的部分。我们使用与Igl等人(2018)相关的变分方法来估计对任务的信念。虽然他们专注于解决一般的POMDP，但我们利用元学习问题强加的额外结构来简化推理，并在新任务中使用后验采样进行探索。

 

3. Meta-RL Problem Statement

　　我们的动机是，在这种情况下，智能体可以利用以前任务中的各种经验，快速适应手头的新任务。样本效率是我们问题陈述的核心，无论是从先前经验的样本数量（元训练效率）还是从新任务的经验量（适应效率）来看。我们通过利用异策RL来实现元训练效率。适应效率要求智能体对其任务的不确定性进行推理，特别是在稀疏奖励设置中。为了捕捉我们对任务的信念中的不确定性，我们学习了先前经验的概率潜在表示。我们在本节中对问题陈述进行了形式化，在第4节中将我们的自适应方法表述为概率推理，并在第5节中解释了我们的方法如何与异策RL算法集成。

　　与以前的元RL公式类似，我们假设任务分布p(τ)，其中每个任务都是马尔可夫决策过程（MDP），由一组状态、动作、转换函数和有界奖励函数组成。我们假设转换和奖励函数是未知的，但可以通过在环境中采取动作来采样。形式上，任务由初始状态分布p(s₀)、转换分布p(s_t+1 | s_t, a_t)和奖励函数r(s_t, a_t)组成。这个问题定义包括具有不同转换函数（例如，具有不同动力学的机器人）和不同奖励函数（例如导航到不同位置）的任务分布。给定从p(τ)中采样的一组训练任务，元训练过程通过以过去转换的历史为条件来学习适应手头任务的策略，我们称之为上下文c。设是任务T中的一个转换，使得包括迄今为止收集的经验。在测试时，策略必须适应从p(τ)中提取的新任务。

 

4. Probabilistic Latent Context

　　我们获取了关于当前任务应该如何在潜在概率上下文变量Z中执行的知识，在此基础上，我们策略调整为π_θ(a|s, z)，以便使其行为适应任务。元训练包括利用来自各种训练任务的数据，学习从新任务的近期经验历史推断Z的值，以及优化策略，以解决Z上的后验给定样本的任务。在本节中，我们描述了元训练推理机制的结构。我们在第5节中讨论了如何使用异策RL算法执行元训练。

 

4.1. Modeling and Learning Latent Contexts

　　为了实现自适应，潜在上下文Z必须对关于任务的显著信息进行编码。回想一下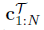，包括迄今为止收集的经验；在本节中，为了简单起见，我们通常会写作c。我们采用了一种摊销变分推理方法（Kingma & Welling，2014；Rezende et al.，2014；Alemi et al.，2016）来学习推理Z。我们训练了一个推理网络q_Φ(z|c)，通过参数化来估计后验p(z|c)。在生成方法中，这可以通过优化q_Φ(z|c)来实现，以通过学习奖励和动态的预测模型来重建MDP。或者，q_Φ(z|c)可以以无模型的方式进行优化，以对状态-动作价值函数进行建模，或者通过任务分配的策略来最大化回报。假设该目标为对数似然，则得到的变分下界为：

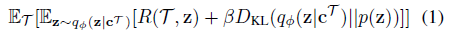
其中p(z)是Z上的单位高斯先验，并且R(τ, z)可以是多种目标，如上所述。KL散度项也可以被解释为对信息瓶颈的变分近似的结果（Alemi et al.，2016），该信息瓶颈约束Z和c之间的互信息。直观地说，该瓶颈约束z仅包含适应手头任务所需的上下文信息，从而减轻对训练任务的过拟合。q_Φ的参数在元训练期间被优化，然后被固定；在元测试时，新任务的潜在上下文只是从收集的经验中推断出来的。

　　在设计推理网络q_Φ(z|c)的结构时，我们希望它具有足够的表达能力，能够捕获任务相关信息的最小足够统计，而不需要建模不相关的依赖关系。我们注意到，完全观察到的MDP的编码可以相对于由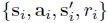组成的采样转换是置换不变的。转换和奖励函数（以及MDP）可以从这种转换的无序集合中重建。因此，一组这样的转换足以训练一个价值函数或推断任务是什么。考虑到这一观察结果，我们为q_Φ(z|c_1:N)选择了一个置换不变表示，并将其建模为独立因子的乘积

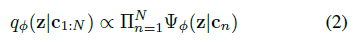
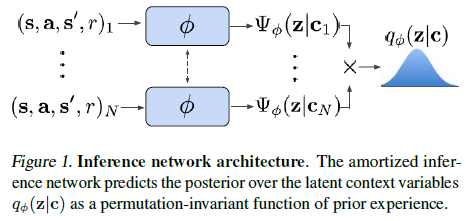
　　为了使该方法易于处理，我们使用高斯因子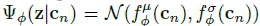，这导致高斯后验。函数f_Φ表示为由Φ参数化的神经网络，它预测作为c_n函数的均值μ和方差σ，如图1所示。

 

4.2. Posterior Sampling and Exploration via Latent Contexts

　　将潜在上下文建模为概率性的，使我们能够在元测试时利用后验采样进行有效的探索。RL探索的后验采样（Strens，2000；Osband et al.，2013）从MDP上的先验分布开始，根据迄今为止的经验计算后验分布，并在回合持续期间执行采样MDP的最优策略，作为一种有效的探索方法。特别地，根据随机MDP最优地动作允许时间上扩展的探索，这意味着即使动作的结果不是任务的即时信息，智能体也可以行动来测试假设。

　　在单任务深度RL设置中，Osband等人(2016)已经探索了后验采样和深度探索的好处，通过自举保持了价值函数上的近似后验。相反，我们的方法PEARL直接推断潜在上下文Z上的后验，如果对重建进行优化，它可以对MDP本身进行编码，如果对策略进行优化，则可以对最优行为进行编码，或者如果对critic进行优化，可以对价值函数进行编码。我们的元训练过程利用训练任务来学习Z上的先验知识，该先验知识捕捉任务上的分布，并学会有效地利用经验来推断新任务。在元测试时，我们最初从先验中采样z，并根据每一回合的z执行，从而以时间扩展和多样化的方式进行探索。然后，我们使用收集到的经验来更新后验，并以一种随着我们的信念缩小而越来越优化的方式继续连贯地探索，类似于后验采样。

 

5. Off-Policy Meta-Reinforcement Learning

　　虽然我们的概率上下文模型可以直接与同策梯度方法相结合，但我们工作的主要目标是实现高效的异策元强化学习，其中元训练和快速自适应的样本数量都是最小的。在先前的工作中，元训练过程的效率在很大程度上被忽视了，这些工作使用了稳定但相对低效的同策算法（Duan et al.，2016；Finn et al.，2017；Gupta et al.，2018；Mishra et al.，2018）。然而，设计异策元RL算法并非易事，部分原因是现代元学习是基于用于自适应的数据分布将在元训练和元测试中匹配的假设。在RL中，这意味着，由于在元测试时，同策数据将被用于调整，因此在元训练期间也应该使用同策数据。此外，元RL需要策略对分布进行推理，以便学习有效的随机探索决策。这个问题本质上无法通过最小化时序差分误差的异策RL方法来解决，因为它们不具有直接优化访问状态分布的能力。相反，策略梯度方法直接控制策略所采取的动作。考虑到这两个挑战，元学习和基于价值的RL的朴素结合可能是无效的。在实践中，我们无法优化这种方法。

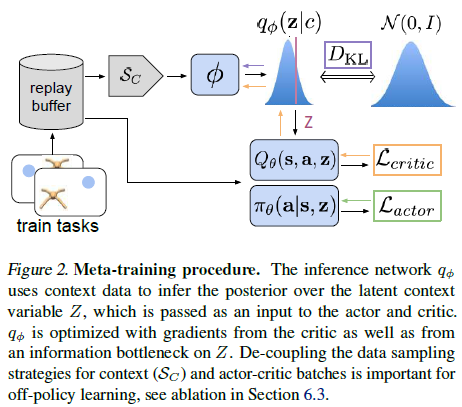
　　如第4.2节所述，我们通过将潜在上下文变量建模为概率变量来解决异策元学习探索决策问题，从而能够通过后验采样进行探索。我们通过注意用于训练编码器的数据不必与用于训练策略的数据相同，来解决异策元训练数据和同策测试时间自适应数据之间的分布变化。策略可以将上下文z视为异策RL循环中状态的一部分，而探索过程的随机性由编码器q(z|c)中的不确定性提供。actor和critic总是用从整个回放缓存B采样的异策数据来训练。我们定义了一个采样器S_c来对上下文批次进行采样，以训练编码器。允许S_c从整个缓存中采样会导致与同策测试数据的分布不匹配过于极端，经验性能受到影响，请参见第6.3节。然而，上下文不需要严格地同策；我们发现，从最近收集的数据的回放缓存中采样的中间策略以更好的效率保留了策略性能。我们在图2和算法1中总结了我们的训练过程。元测试在算法2中进行了描述。

 

5.1. Implementation

　　我们在soft actor-critic算法（SAC）（Haarnoja et al.，2018）的基础上构建了我们的算法，这是一种基于最大熵RL目标的异策actor-critic方法，该方法用策略的熵来增加传统的贴现收益之和。SAC具有良好的样本效率和稳定性。

　　我们使用重参数化技巧（Kingma & Welling，2014）通过采样的z来计算q_Φ(z|c)参数的梯度，将推理网络q(z|c)的参数与actor π_θ(a|s, z)和critic Q_θ(s, a, z)的参数联合优化。我们使用Bellman更新中的梯度为critic训练推理网络。我们根据经验发现，训练编码器以恢复状态-动作价值函数的效果优于优化编码器以最大化actor回报或重建状态和奖励。critic的损失可以写为，

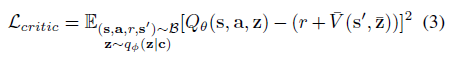
其中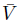是目标网络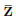，表示没有通过它计算的梯度。actor损失几乎与SAC相同，额外依赖于z作为策略输入。

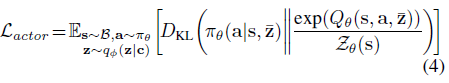
　　请注意，用于推断q_Φ(z|c)的上下文与用于构建actor和critic损失的数据不同。如第5节所述，在元训练期间，我们分别对上下文批次和actor-critic批次进行采样。具体地，上下文采样器S_c从最近收集的一批数据中均匀地采样，每1000个元训练优化步骤进行一次回忆。actor和critic使用从整个回放缓存均匀抽取的一批转换进行训练。

 

6. Experiments

 

6.1. Sample Efficiency and Performance

 

6.2. Posterior Sampling For Exploration

 

6.3. Ablations

 

7. Conclusion