Incorporating Learnable Membrane Time Constant to Enhance Learning of Spiking Neural Networks

ICCV 2021（同组的工作，已集成入SpikingJelly平台）

 

Abstract

　　由于时间信息处理能力、低功耗和高生物合理性，脉冲神经网络（SNN）引起了巨大的研究兴趣。然而，为SNN制定高效和高性能的学习算法仍然具有挑战性。大多数现有的学习方法只学习权重，并且需要手动调整膜相关参数，以确定单个脉冲神经元的动力学。这些参数通常被选择为对所有神经元都相同，这限制了神经元的多样性，从而限制了生成的SNN的表现力。在本文中，我们从观察到的膜相关参数在大脑区域中不同的现象中获得灵感，并提出了一种训练算法，该算法不仅能够学习突触权重，还能够学习SNN的膜时间常数。我们表明，加入可学习的膜时间常数可以使网络对初始值不那么敏感，并可以加快学习。此外，我们重新评估了SNN中的池化方法，发现最大池化不会导致显著的信息丢失，并且具有低计算成本和二值兼容性的优点。我们在传统静态MNIST、Fashion-MNIST和CIFAR-10数据集以及神经形态N-MNIST，CIFAR10-DVS和DVS128 Gesture数据集上评估了所提出的图像分类任务方法。实验结果表明，所提出的方法在几乎所有数据集上都优于最先进的精度，使用更少的时间步长。我们的代码可在https://github.com/fangwei123456/Parametric-Leaky-Integrate-and-Fire-Spiking-Neuron。

 

1. Introduction

　　脉冲神经网络（SNN）被视为第三代神经网络模型，更接近大脑中的生物神经元[38]。与神经元和突触状态一起，在SNN中也考虑了脉冲时间的重要性。SNN由于其独特的性质，例如时序信息处理能力、低功耗[49]和高生物可信度[16]，近年来越来越引起研究人员的极大兴趣。然而，为SNN制定高效和高性能的学习算法仍然具有挑战性。

　　通常，SNN的学习算法可以分为无监督学习、有监督学习、基于奖励的学习和人工神经网络（ANN）到SNN的转换方法。无论如何，我们发现大多数现有的学习方法只考虑学习突触相关参数，如突触权重，并将膜相关参数视为超参数。这些与膜相关的参数，如决定单个脉冲神经元动力学的膜时间常数，通常被选择为对所有神经元都相同。然而，请注意，大脑各区域的神经元脉冲存在不同的膜时间常数[39，9，30]，这被证明对工作记忆的表示和学习的公式化至关重要[20，53]。因此，简单地忽略SNN中的不同时间常数将限制神经元的异质性，从而限制最终SNN的表现力。

　　在本文中，我们提出了一种训练算法，该算法不仅能够学习突触权重，而且能够学习SNN的膜时间常数。如图1所示，我们发现突触权重和膜时间常数的调整对神经元动力学有不同的影响。我们表明，加入可学习的膜时间常数能够增强SNN的学习。

　　本文的主要贡献概括如下：

　　1） 我们提出了一种基于反向传播的学习算法，该算法使用具有可学习膜参数的脉冲神经元，称为参数LIF（PLIF）脉冲神经元，它可以更好地代表神经元的异质性，从而增强SNN的表现力。我们发现，由PLIF神经元组成的SNN对初始值更具鲁棒性，并且比由具有固定时间常数的神经元组成的SNN学习更快。

　　2） 我们重新评估了SNN中的池化方法，并否定了先前的结论，即最大池会导致显著的信息丢失。我们发现，与平均池相比，最大池能够更好地保持神经元发放的异步特性，并降低计算成本。我们的实验表明，最大池的性能与平均池相当。

　　3） 我们在神经网络中广泛使用的传统静态MNIST [32]、Fashion-MNIST [59]、CIFAR-10 [31]数据集和神经形态N-MNIST [44]、CIFAR10-DVS [36]、DVS128 Gesture [1]数据集上评估了我们的方法，这些数据集侧重于验证网络的时序信息处理能力。所提出的方法在几乎所有测试数据集上都超过了最先进的精度，使用更少的时间步长。

 

2. Related Works

Unsupervised learning of SNNs 

Reward-based learning of SNNs 

ANN to SNN conversion 

Supervised learning of SNNs 

Spiking neurons and layers of deep SNNs 

 

3. Method

　　在本节中，我们首先简要回顾了第3.1节中的LIF模型，并在第3.2节中分析了突触权重和膜时间常数的影响。然后在第3.3节至第3.5节中介绍了参数LIF模型以及SNN的网络结构。最后，我们在第3.6节和第3.7节中描述了脉冲最大池和SNN学习算法。

 

3.1. Leaky Integrate-and-Fire model

 

3.2. Function comparison of synaptic weight and membrane time constant

 

 

3.3. Parametric Leaky Integrate-and-Fire model

　　我们提出了参数LIF（PLIF）脉冲神经元模型，以学习SNN的突触权重和膜时间常数。PLIF神经元的动力学可由公式(1)描述。

　　具有PLIF神经元的SNN遵循三个规则：

　　(1). 膜时间常数在训练期间自动优化，而不是在训练之前手动设置为超参数。

　　(2). SNN中同一层神经元共享膜时间常数，这在生物学上是合理的，因为相邻神经元具有相似的性质。

　　(3). 不同层神经元的膜时间常数不同，使得神经元的相频率响应性不同。

　　事实上，所提出的规则能够在有效控制计算成本的同时增加神经元的异质性和产生的SNN的表现力。

　　对于SNN中PLIF神经元的数值模拟，我们需要考虑在时间上离散的参数动力学版本。具体而言，通过包括阈值触发的发放机制和发放后膜电位的重置，我们可以用以下方程描述各种脉冲神经元的动力学：

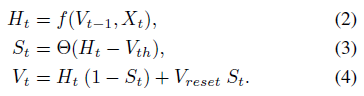
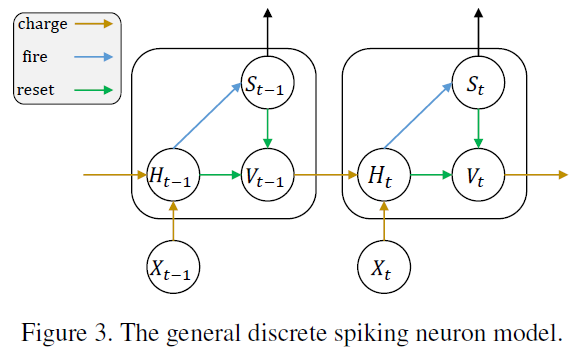
为了避免混淆，我们使用H_t和V_t分别表示神经元动力学之后和在时间步骤 t 触发脉冲之后的膜电位。X_t表示外部输入，V_th表示发放阈值。S_t表示时间 t 处的输出脉冲，如果存在脉冲，则等于1，否则等于0。公式(3)描述了脉冲生成过程，其中Θ(x)是Heaviside阶跃函数，由Θ(x) = 1（对于x ≥ 0）和Θ(x) = 0（对于x < 0）定义。公式(4)说明了膜电位在引发脉冲后返回V_reset，这被称为硬重置，并广泛用于深SNN[33]。

　　如图3所示，公式(2)-(4)建立了一个通用模型来描述离散脉冲神经元的动作：充电、放电和复位。具体而言，公式(2)描述了神经元动力学，不同的脉冲神经元模型具有不同的函数f(·)。例如，LIF神经元和PLIF神经元的函数f(·)为：

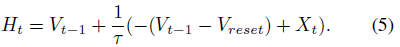
　　对于PLIF神经元，直接优化公式(5)中的膜时间常数 τ 可能导致分母中的数值不稳定性。此外，公式(5)作为公式(1)的离散版本，仅当时间步长dt小于 τ，即τ > 1时才是有效的近似值，[47, 61]忽略了这一点。为了避免上述问题，我们将公式(5)重新表述为具有可训练参数a的以下等式：

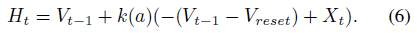
这里，k(a)表示clamp函数，k(a) ∈ (0, 1)确保。在我们的实验中，k(a)是sigmoid激活函数，即。

 

3.4. RNN-like Expression of LIF and PLIF

　　LIF和PLIF神经元具有与循环神经网络类似的功能。具体地，当V_reset ＝ 0时，LIF神经元和PLIF神经元的神经元动力学（公式(5)）可以写成：

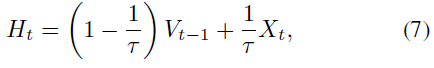
其中积分过程使LIF和PLIF神经元能够记住当前输入信息，而泄漏过程可以被视为忘记了过去的一些信息。公式(7)表明，记忆和遗忘之间的平衡由膜时间常数控制，膜时间常数在长短期记忆（LSTM）网络中起着类似的作用[23]。

 

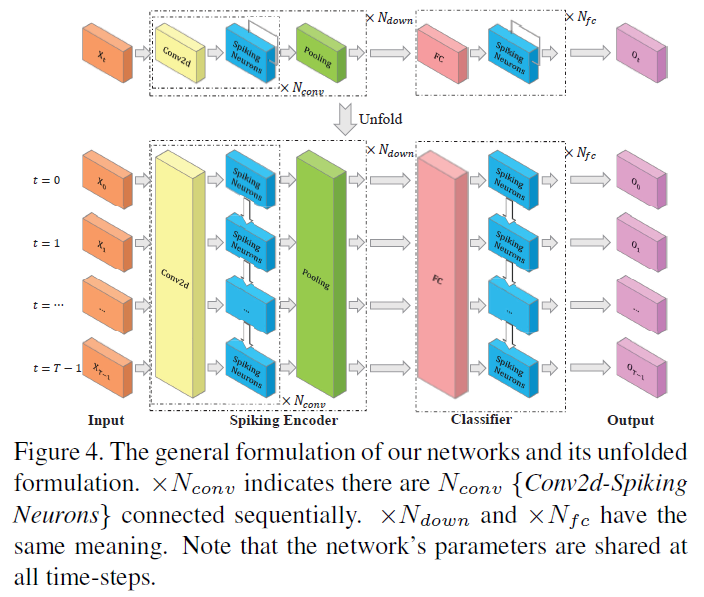
3.5. Network Formulation

　　我们在本文中提出了构建SNN的一般公式，如图4所示。SNN包括脉冲编码器网络和分类器网络。脉冲编码器网络由N_down向下采样模块组成，每个模块包含N_conv重复{Conv2d-Spiking Neurons}和一个池化层。脉冲编码器可以从输入中提取特征，并将其转换为不同时间步长的发放脉冲。分类器网络由N_fc个重复的{FC-Spiking Neurons}组成。这里Conv2d表示2D卷积层，FC表示全连接层。许多先前的工作[11, 34, 54, 64, 8, 19]使用泊松编码器将图像转换为脉冲作为输入，而[50]表明，这种编码将可变性引入网络的发放，并削弱其性能。类似于[50, 58, 47]，输入直接馈送到我们的网络，而不首先转换为脉冲。在这种情况下，图像脉冲编码由第一个{Conv2d-Spiking Neurons}模块完成，它可以看作是一个可学习的编码器。注意，突触连接（包括卷积层和全连接层）是无状态的，而脉冲神经元层在时域中具有自连接，如图4所示的展开网络公式。所有参数在所有时间步长都是共享的。

 

3.6. Spike Max-Pooling

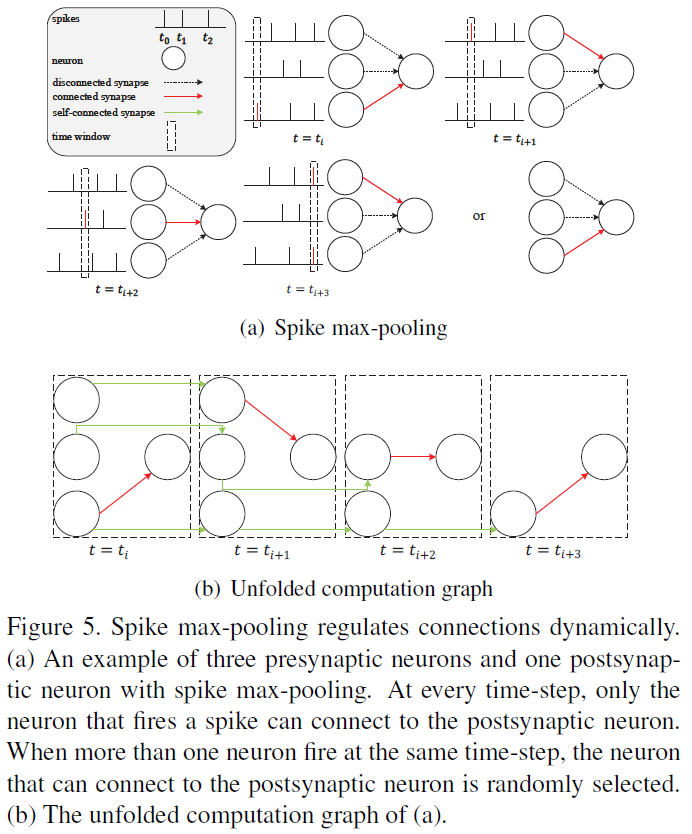
　　池化层被广泛用于减少特征图的大小，并提取卷积ANN以及SNN中的紧凑表征。大多数先前的研究[51，8，48]倾向于使用SNN中的平均池，因为他们发现SNN中最大池会导致显著的信息丢失。我们认为，最大池与SNN的时序信息处理能力一致，可以提高SNN在时间任务中的拟合能力，并降低下一层的计算成本。

　　具体来说，在我们的模型中，最大池层位于脉冲神经元层之后（图4），最大池操作在脉冲上进行。与在平均池窗口中向下一层传输信息的所有神经元不同，只有在最大池窗口中发放脉冲的神经元才能向下一个层传输信息。因此，最大池化层引入了赢者通吃机制，允许发放的神经元与下一层通信，而忽略池化窗口中的其他神经元。另一个吸引人的特性是，最大池化层将动态调节连接（图5）。发出脉冲后，脉冲神经元的膜电位V_t将恢复到V_reset。由于再充电需要时间，脉冲神经元很难再次发放。然而，如果最大池窗口中的神经元异步启动，它们将依次连接到突触后神经元，这使得突触后神经元类似于连接一个连续启动的突触前神经元，更容易启动。通过最大池化实现的空间域中的赢者通吃机制和时间域中的时变拓扑可以提高SNN在时间任务中的拟合能力，例如对CIFAR10-DVS数据集进行分类。值得注意的是，最大池化层的输出仍然是二值的，而平均池化层输出是浮点的。通过用逻辑AND &代替乘法，可以加速脉冲上的矩阵乘法和逐元素乘法运算，这也是SNN与ANN相比的优势。

 

3.7. Training Framework

 

4. Experiments

　　我们在传统静态MNIST、Fashion-MNIST和CIFAR-10数据集以及神经形态N-MNIST，CIFAR10-DVS和DVS128 Gesture数据集上评估了具有PLIF神经元和脉冲最大池的SNN在分类任务中的性能。有关训练的更多详情，请参阅补充资料。

 

4.1. Network Structure

　　不同数据集的SNN网络结构如表1所示。我们将所有Conv2d层的核大小设置为3，步长设置为1，填充设置为1。对于CIFAR-10数据集，Conv2d层的输出通道为256，对于所有其他数据集，输出通道为128。在每个Conv2d层之后添加批归一化（BN）层。由于BN层的参数可以在其前Conv2d层中吸收[50]，我们进行推断时可以去除SNN中的BN。所有池化层都将核大小设置为2，步长设置为2。对于所有网络，第一个FC层的输出特征是输入特征的四分之一，第二个FC层的输入特征是M · C，其中C是类数，M是表示一个类的群体的神经元。在每个FC层之前放置dropout层[34]。在输出脉冲神经元层之后的投票层用于增强分类鲁棒性。投票层通过平均池实现，核大小=M，步长=M。我们为所有数据集设置M=10。我们使用平均汇集来实现民主投票，使少数服从多数。使用最大集合投票可能会导致独裁，因为少数人不会参与计算图（见图5），使用M个神经元代表一个类别将退化为使用一个神经元。

 

4.2. Comparison with the State-of-the-Art

 

 

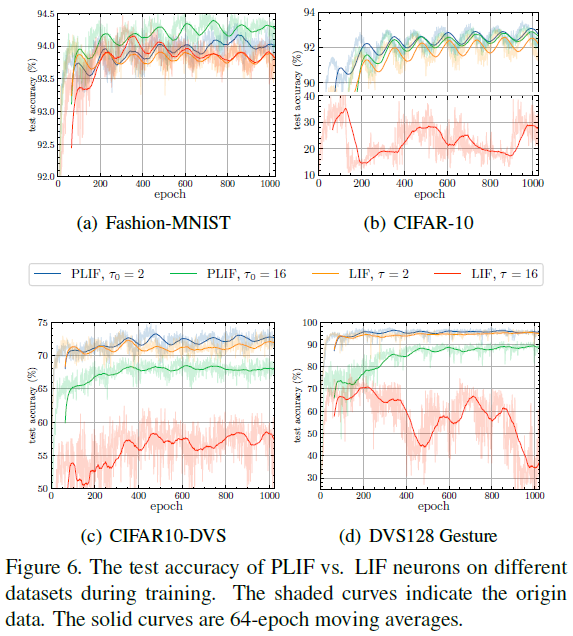
4.3. Ablation Study

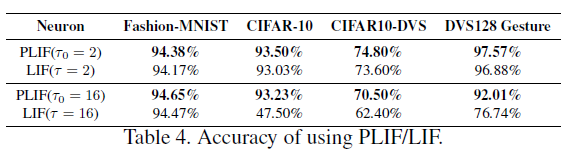
　　我们在四个具有挑战性的数据集上进行了广泛的消融研究，以评估PLIF神经元和最大池化。我们首先研究了PLIF神经元的作用。在本实验中，我们分别用PLIF神经元和LIF神经元训练相同的SNN，并比较测试的准确性。如表4所示，如果PLIF神经元的初始膜时间常数τ₀设置为等于LIF神经元的膜时间常数，则PLIF神经元SNN的测试精度始终高于LIF神经元。这是由于学习后不同层中PLIF神经元的膜时间常数可能不同，这更好地代表了神经元的异质性。图6说明了训练期间PLIF与LIF神经元的测试准确性。可以看出，如果膜时间常数的初始值不合理（红色曲线），则具有LIF神经元的SNN的准确性和收敛速度会严重下降。相比之下，PLIF神经元可以学习适当的膜时间常数并获得更好的性能（绿色曲线）。

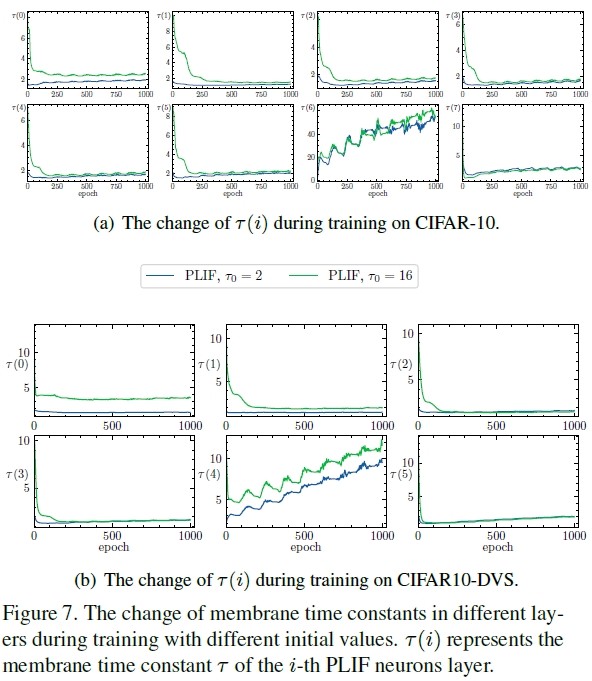
　　为了分析PLIF神经元初始值的影响，我们展示了每层神经元的膜时间常数在学习过程中如何相对于不同的初始值发生变化。如图7所示，每个层中具有不同初始值的膜时间常数在训练期间趋于聚集，这表明PLIF神经元对初始值具有鲁棒性。请注意，图7(a)中的τ(6)和图7(b)中的τ(4)趋向于无穷大。这可以解释如下。在两个SNN中具有膜时间常数τ(4)和τ(6)的PLIF神经元位于具有权重W_fc的第一个FC层之后。我们检查训练日志，发现的分布、均值和方差（τ = τ(4)或τ(6)）在几十个epoch后收敛（见补充材料）。参考PLIF神经元的动力学（公式(5)），X_t = W_fcI_t和，我们可以找到。这意味着第一个FC层之后的PLIF神经元正在学习成为IF神经元。

　　我们进一步研究了最大池效应。表5比较了四个具有挑战性的数据集上所提出的SNN与最大池/平均池的准确性。最大池的性能与平均池的性能相似，这表明先前关于最大池导致SNN中显著信息丢失的结论是不合理的。值得注意的是，最大池在CIFAR-10、CIFAR10-DVS和DVS128手势数据集上的精度略高，显示出其在复杂任务中的更好拟合能力。

 

5. Conclusion

　　在这项工作中，我们提出了PLIF神经元，以将可学习的膜时间参数纳入SNN。我们表明，在静态和神经形态数据集上，具有PLIF神经元的SNN优于最先进的比较方法。此外，我们发现由PLIF神经元组成的SNN比由LIF神经元组成的SNN对初始值更为鲁棒，并且学习速度更快。我们还重新评估了SNN中最大池和平均池的性能，并发现之前的工作低估了最大池的性能。我们提出在SNN中使用最大池，因为它具有更低的计算成本、更高的时间拟合能力，以及接收脉冲和输出脉冲的特性（而不是平均池的浮点值）。

 

Supplementary Materials

1. Reproducibility

　　所有实验均由SpikingJelly实现[4]。所有的源代码和培训日志都可以在GitHub上找到。为了最大化复现性，我们在所有代码中使用相同的种子。

 

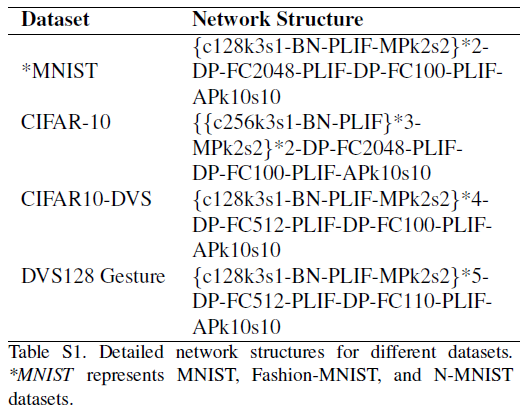
2. Network Structure Details

 

3. Training Algorithm to Fit Target Output

　　在定义了脉冲生成过程的导数之后，SNN的参数可以像在ANN中一样通过梯度下降算法进行训练。分类是本文的任务，以及ANN和SNN的其他任务，可以被视为在给定特定输入时优化网络参数以适应目标输出。用于SNN以拟合目标输出的梯度下降算法在正文中导出（公式(16)和公式(17)），如下所示：

　　这里，损失函数是Y和S之间的距离测量，例如，正文中的均方误差（MSE）。 

 

4. Introduction of the Datasets

MNIST

Fashion-MNIST

CIFAR-10

N-MNIST

CIFAR10-DVS

DVS128 Gesture

 

5. Preprocessing

Static Datasets. 我们在所有静态数据集上应用数据归一化，以确保输入图像具有零均值和单位方差。此外，在MNIST和CIFAR-10上进行随机水平翻转和裁剪，以避免过拟合。我们没有在Fashion-MNIST上使用这些增强，因为这个数据集中的图像是整洁的。

Neuromorphic Datasets. 神经形态数据集中的数据通常采用地址事件表征（AER）E(x_i, y_i, t_i, p_i) (i=0, 1, … , N-1)以表示异步流中的事件位置、时间戳和极性。由于事件数量很大，例如CIFAR10-DVS中的事件数量超过一百万，我们将事件分成T个切片，每个切片中的事件数几乎相同，并将事件整合到帧中。新的表征F(j, p, x, y) (0 ≤ j ≤ T-1)是第 j 个切片中事件数据的总和：

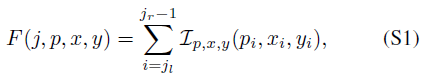
其中是一个指示函数，只有当(p, x, y) = (p_i, x_i, y_i)时才等于1。j_l和j_r是第 j 个切片中的最小和最大时间戳索引。，如果j < T-1，，如果j = T-1，则为N。这里是向下取整操作。注意，T也是我们实验中的时间步长。

　　用于预处理神经形态数据集的类似事件到帧集成方法广泛用于ANN [6，13，12]和SNN [16，17，1，19，6，7，10]。N-MNIST和CIFAR10-DVS的正文表3中[16]的T是根据他们的论文手动计算的。具体地说，他们说明了通过在每5ms内累积脉冲序列来降低时间分辨率，并且N-MNIST和CIFAR10DVS的时间范围（us）分别为[2290901, 315348]和[1149758, 1459301]。

 

6. Hyper-Parameters

　　我们使用学习率为0.001的Adam [8]优化器和T_schedule = 64的余弦退火学习率计划[11]。批处理大小设置为16以减少内存消耗。dropout层的drop概率p为0.5。PLIF神经元的clamp函数为和替代梯度函数为，因此。我们为所有神经元设置V_reset＝0和V_th＝1。我们注意到，以前的一些工作，例如[15][16]，针对不同的任务微调了V_th，这是不必要的。具体来说，作为并且V受到可训练权重的直接影响，设置V_th=1实现了权重的隐式归一化，这可以减轻爆炸和消失的梯度问题。正如Zenke和Vogels[23]所发现的，当计算梯度时，通过将其从计算图中分离来忽略神经元重置可以提高性能，我们也分离了神经元重置中的S_t。

 

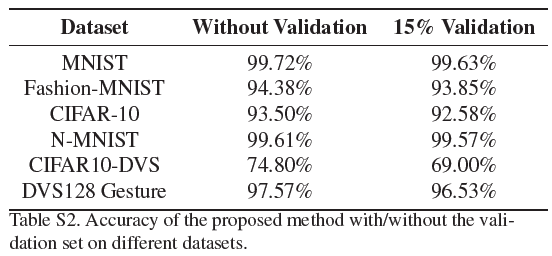
7. Accuracy with a Validation Set

　　正文表2中的性能比较是通过在训练集上训练，在测试集上交替测试，并记录最大测试精度来获得的。本文和最先进的方法都使用这种方式来报告性能。然而，这种准确性被高估了。在这里，我们还报告了验证的准确性，这是通过将原始训练集拆分为新的训练集和验证集、在新的训练集中进行训练、交替地在验证集上进行测试以及使用实现最大验证准确性的模型仅在测试集上记录一次测试准确性而获得的。我们使用原始训练集中每个类85%的样本作为新的训练集，并将其余15%的样本作为验证集。表S2显示了采用和不采用拟议方法验证集的准确度。正文表2和表S2中的实验结果表明，所提出的方法在几乎所有数据集上都优于最先进的精度。

 

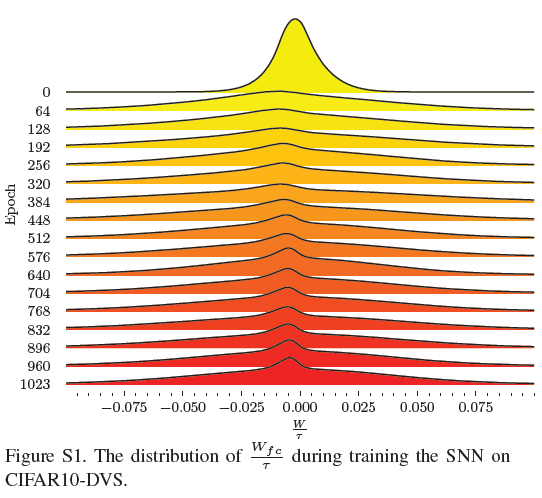
8. Distribution of the First 

　　在正文的第4.3节中，我们发现第一个FC层之后的PLIF神经元正在学习成为IF神经元（并且收敛）。为了说明收敛性，我们在图S1中显示了在CIFAR-10DVS上训练SNN期间的分布。在其他数据集上的分布以相同的方式收敛。

 

9. Visualization of Spiking Encoder

 

10. Relations between different Encoders

　　泊松编码器是发放率编码方法之一，广泛用于SNN [3，9，14，24，1，5]中，将图像编码为脉冲。给定图像像素p ∈ [0, 1]，以概率p激发时间步骤 t 处的编码脉冲S_t。因此，整个时间步长T期间脉冲数量的期望值为。在我们提出的SNN中，输入被直接馈送到网络，而无需首先转换为脉冲，并且图像脉冲编码由第一个{Conv2d-Spiking Neurons}模块（省略BN）完成，该模块可以被视为可学习编码器。在这里，我们将该编码器表示为ENC_l。如果我们将Conv2d设置为不可学习的，通道数=核大小=1，核权重为常数w > 0，脉冲神经元设置为阈值电位V_th且V_reset=0的IF神经元，则该模块的脉冲数的期望值为，其中表示向上取整操作。我们可以发现（V_th = w = 1），这表明ENC_l可以近似Possion编码器在发放率编码中的函数。

　　[18，20，21，22]中使用的延迟编码器是一种具有代表性的时间编码方法。延迟编码器在时间步长t_p将图像像素p编码为脉冲。因此，输入的信息被编码在脉冲的精确发射时间中。t_p通常与输入强度p成反比，例如，且T_max是编码周期。我们还可以发现，对于给定的输入p，ENC_l的第一次发放时间是，这满足输入强度p越大，脉冲发放越快。事实上，延迟编码器是一种极其简化的可学习编码器，具有直接输入的图像。在本文中，所提出的可学习编码器具有可学习的权重和更多的信道，能够将图像编码为具有更多语义信息的复杂脉冲模式，例如，保留手势但丢弃DVS128 Gesture数据集的样本玩家（见图S5）。