The value of what's to come: Neural mechanisms coupling prediction error and the utility of anticipation
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Science advances, no. 25 (2020)
Abstract
有期待的事情是幸福的基石。对未来奖励(例如即将到来的假期)的期望通常比经验本身更令人满足。理论表明,预期的效用是各种行为的基础,从有益的信息寻求到有害的成瘾,不一而足。但是,神经系统如何计算预期效用仍不清楚。我们分析了人类参与者执行一项任务的大脑活动,该任务涉及选择是否接收可预测未来令人满意的结果的信息。使用计算模型,我们显示了三个大脑区域协调预期效用。具体而言,腹侧前额叶皮层跟踪预期效用的值,多巴胺能中脑与增强预期的信息相关,而持续的海马体活动介导这些区域之间的功能耦合。我们的研究结果表明了先前尚无定论的预测对决策的影响的神经基础,并且对一系列与风险和时延偏好相关的现象进行了统一。
INTRODUCTION
“Pleasure not known beforehand is half-wasted; to anticipate it is to double it.”
– Thomas Hardy, The Return of the Native
标准的经济理论认为,奖励即将来临(例如现在就餐)比延迟(例如明天就餐)时更具吸引力,并预测人们总是会立即消费奖励。例如,在设计可以通过了解人类心灵各方面有效规划其未来的人工智能系统的设计中,这种所谓的时间折扣已获得了巨大的成功。
但是,现实生活中的行为更为复杂(1-3)。人类和其他动物有时会倾向于故意推迟愉快的经历[例如,为明天节省一块蛋糕或延迟一次亲吻名人的机会(1)],这与简单的时间折扣的预测相矛盾。
行为经济学中一个有影响力的替代思想是人们享受或品尝导致奖励的时刻(1, 2, 4-7)。就是说,人们体验到一种积极的效用,即所谓的期望效用,这种效用赋予了等待奖励所花费的时间。期望效用不同于标准决策和强化学习理论中经过充分研究的未来奖励的期望值(即,奖励的折扣值),后者的效用仅来自奖励而不是其期望。至关重要的是,在期望效用理论(1)中,将两个单独的效用(即期望和奖励)相加在一起构成总价值。期望效用的增加值自然地解释了为什么人们偶尔更喜欢延迟奖励(例如,因为我们可以通过现在保存来享受到明天再吃蛋糕的期望)(1),以及许多其他人类行为,例如寻求信息和成瘾(4, 8)。
尽管该理论具有清晰的数学表述及其对行为的解释能力,但我们对期望效用如何在大脑中产生的信息知之甚少。尽管先前的研究描述了神经活动与未来奖励的期望有关(5, 9-14),但尚不清楚这种活动是否或如何与期望效用有关。这种知识真空的一个主要原因是在实验室环境中建立行为的挑战,这种行为是由期望效用驱动的[请参见(5)]。值得注意的是,最近的研究(6-8)已经在期望效用和信息寻求行为之间建立了牢固的联系,这现在使我们能够正式测试大脑如何动态构建期望效用。
在此,我们研究了由奖励期望的效用引起的价值计算的神经生物学基础,以及获得的信息如何调节这种期望效用。为此,我们将行为任务,计算模型和功能性磁共振成像(fMRI)结合在一起。我们将期望效用(1)的计算模型(8)拟合为任务行为,并为每个参与者使用最优模型对大脑中期望效用的时间过程进行预测。然后,我们将该预测信号与实际fMRI数据进行了比较,发现腹侧前额叶皮层(vmPFC)编码了期望效用信号的时间动态,而多巴胺能中脑编码了一个报告奖励期望变化的信号。奖励预测误差(RPE)在强化学习理论中被广泛解释为教学信号(15),但我们的模型预测,它还可以起到增强期望效用的作用,从而推动行为。我们显示,海马体介导这种效用的增强,是vmPFC和多巴胺能中脑之间功能性偶联的底物(16, 17)。我们提出这些区域将奖励信息与期望效用联系起来,而海马体,记忆和未来想象力之间的牢固概念联系则支持了行为经济学的建议,即期望效用与未来奖励的生动想象力有关(18-20)。
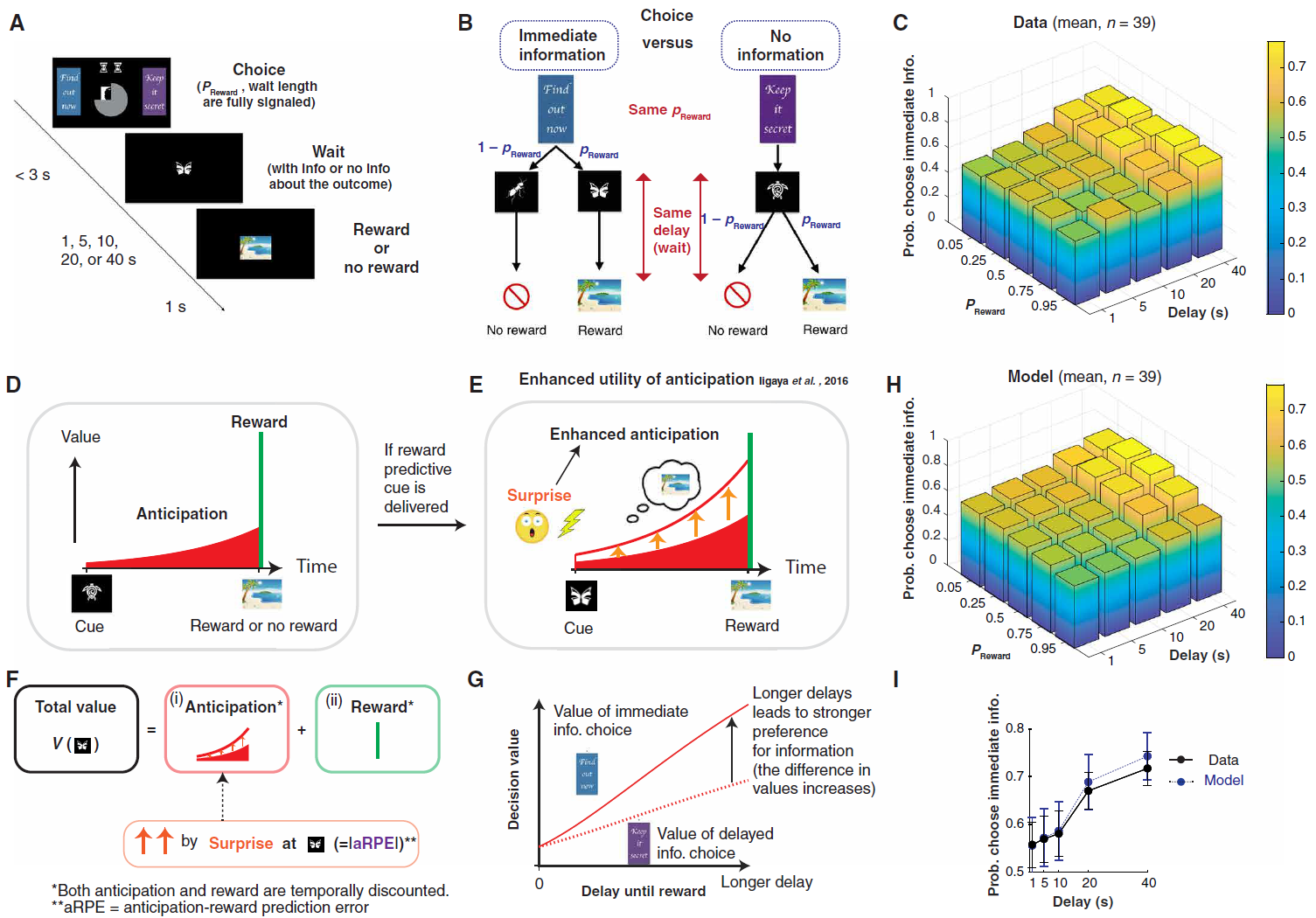
图1. 期望效用推动了对高级信息的偏好。(A) 任务。向参与者展示了即时信息目标("立即查找")和无信息目标("保持秘密"),以及两个中央刺激信号,这些信号指示了奖励概率以及等待奖励的持续时间或无奖励到达。在整个等待期间都将显示一个象征性的图像提示,直到出现奖励图像或表示没有奖励的图像为止。(B) 即时信息目标之后是预测即将到来的奖励或没有奖励的线索(奖励预测提示或无奖励预测提示)。无信息目标后面是没有奖励结果暗示的信息(无信息提示)。(C) 平均行为。在较长的延迟条件下,参与者表现出对高级信息的强烈偏好[方差双向分析(ANOVA), F4950 = 10.0]。奖励概率的影响(F4950 = 0.35,P > 0.05)显示出不同的依赖性(图S4)。(D到G) 计算模型(8)。(D) 在(1)之后,每个提示的值由以下各项的总和确定:(i) 等待奖励时可以消耗的期望效用(红色)和(ii) 奖励消耗本身的价值(绿色)的总和。(E和F) 如果给出了奖励预测提示,则在整个延迟周期(橙色向上箭头)中的期望都会增强。增加效果由惊奇量化,与aRPE等式1的绝对值成比例。(G) 模型预测,在更长的延迟条件下,两个目标之间的值差异会更大(8)。(H) 使用分层贝叶斯拟合程序(8)建模的偏好均值。(I) 模型(蓝色)捕获数据中延迟条件的影响(黑色)。误差线表示参与者的均值和标准差(n = 39)。关于概率条件的影响参见图S2,关于其他经典模型如何无法解释行为参见图S1。
RESULTS
Participants prefer to receive advanced information about upcoming reward
我们使用了行为任务的一种变体,该变体以前与期望效用相关联(图1A)。简而言之,我们的任务根据奖励概率和延迟到结果的持续时间,检查参与者如何改变其解决未来可喜结果不确定性的偏好(请参见"材料和方法")。参与者在条件(概率和奖励结果延迟)方面具有充分的知识来做出决策,每个试验都通过简单的视觉刺激来表示。为每个试验随机选择条件——从0.05, 0.25, 0.5, 0.75和0.95中随机采样概率,并从1, 5, 10, 20和40 s中随机采样直至奖励或无奖励交付的等待时间。
在每个试验中,参与者都在即时信息目标(被标为"立即查找")和无信息目标("保持秘密")之间进行选择。如果选择了即时信息目标,则会在等待期间显示两个提示之一,每个提示都唯一地表明奖励是否会到达(图1B, 左)。如果选择了无信息目标,则在等待期间屏幕上会显示一个单独的非预测性提示,其中不包含有关即将发生的结果的信息(图1B, 右),最终是奖励或无奖励。奖励图像是从先前验证的奖励图片(8, 21)中随机采样的,因此交付时会立即消耗(通过查看)。没有奖励的结果通过中立的形象来表示。
在这种设计中,参与者的选择既不会影响最终的奖励结果,也不会影响延迟的持续时间(图1B)。奖励概率和延迟时间都是预先确定的,并在每次试验开始时告知参与者。参与者只能选择是否想在延误之前获得有关是否会获得奖励的知识。因此,旨在最大化获得奖励机会的标准决策理论不会预测对这两个选择的偏好,因为在这两个选择中获得奖励的概率(因此,期望价值)是相同的(请参见图S1, A到C)。因此,具有常规时间折扣的模型不会预测选择偏好。
与传统理论的预测相反,我们发现参与者表现出对高级信息的偏好。此外,与先前的发现(22-24)一致,对即时信息的偏好随着延迟时间的增加而增加(图1,C和I)(8, 25)。
Our computational model that links advanced information to the utility of anticipation accounts for behavioral data
先前的研究(6, 8)表明,对于获取高级信息的偏好可以通过期望效用的经济学概念来解释(1, 2, 4, 5, 26)。尽管基于标准价值的决策理论将价值分配给了奖励本身的消耗,但是期望效用理论也将效用价值分配给了导致获得奖励的时刻(图1D;请参见"材料和方法"中的等式1)。尽管期望效用的数学框架可以接受更广泛的解释,但期望效用的一种可能的心理根源是在等待令人愉悦的结果时的愉悦主观感觉(1)。在此,我们的目标是通过识别介导期望效用的神经过程来填补我们目前的理解空白。
尽管期望效用自然地解释了人们为什么会延迟领取奖励的原因(因为他们在等待时会消耗期望效用),但原始表述并不一定解释了人们对于获得有关概率结果的高级信息的偏好。该模型仍然预测任务中两个选择之间的差异,因为期望效用与奖励概率成线性比例(实际结果的期望价值就是这种情况),导致两个选择的平均价值相同(8)(如图S1, D至F所示)。这是正确的,因为信息在原始表述中起着很小的作用。
为了更好地说明期望效用,我们最近提出并验证了对该原始公式的轻微修改(8)。考虑一种情况,在这种情况下,可能会或可能不会提供未来的奖励,但是早期信号解决了不确定性,告诉参与者将肯定地提供奖励。对理论的修改是,通过与信息信号关联的(在这种情况下为正)预测误差,可以增强对未来奖励的期望效用。这种基于惊奇的期望效用增强受到实验观察的启发,这些意外信息可以使动物变得兴奋,并会一直保持这种状态,直到获得奖励为止(25)。没有此类信息等待特定奖励的动物不会表现出类似的兴奋程度(25)。这样的结果可能导致动物自相矛盾地倾向于选择较少的回报(平均),但更令人惊讶的是,选择[例如(3, 25)]。
我们通过使用RPE概念在数学上构造了与提高期望效用有关的惊喜。每当参与者收到有关未来奖励(或无奖励)的高级信息时,参与者都会体验到RPE,RPE由以下两者之间的差异定义:(i) 根据新信息的到来而更新的未来价值;以及(ii) 在新信息到来之前预期的未来价值。在标准理论中,RPE是根据奖励的价值来计算的;在我们的模型中,它是根据期望和奖励效用计算的(等式5)。因此,我们将模型的预测误差信号称为期望+奖励预测误差(aRPE)信号。在我们的计算模型中,此aRPE量化了与期望效用的增强相关的惊喜。遵循传统的预测误差到惊喜的映射(27),该模型通过aRPE的绝对值来量化惊喜,因为意外的负面结果(负aRPE)可能与意外的积极结果(正aRPE)一样令人惊讶。这还避免了不合理的影响,例如通过与负aRPE相乘将负期望变成正期望。因此,增强的最简单表达之一是假定期望效用通过aRPE的绝对值线性增强(参见"材料和方法"中的等式1和2)。
重要的是要注意,aRPE(或标准RPE)应该是仅持续很短一段时间的相位信号。但是,动物可以在整个期望阶段保持兴奋(25),因此在模型中,期望的增强在整个等待阶段(8)得以维持(等式1和2)。因此,该模型预测,与提高期望效用相关的信号将是aRPE绝对值的延长表示(或与惊奇程度成正比的延长信号)。此类信号可能会在除编码相位aRPE的区域之外的其他区域进行编码。稍后我们回到这个问题。
在我们的任务中,对遵循即时信息目标的未来结果进行预测的提示会产生多巴胺能aRPE,并触发对期望效用的增强。另一方面,遵循无信息目标的非预期提示不会生成RPE,因此不会触发任何提升(图S1, G至I)。因此,该模型预测,参与者在经历收到即时信息目标之后的奖励预测提示后,其期望效用得到增强,而参与者在经历收到无信息目标之后的无信息提示后,其期望效用的默认值由奖励的概率加权。由于持续的增强,该模型预测即时信息目标和无信息目标之间的值差在较长的延迟条件下(至少在没有强折扣的情况下)会更大,从而导致对优先选择权的偏好增加。立即信息以更长的延迟条件为目标(图1G)(8)。
我们使用分层贝叶斯方案(8)使该模型适合参与者的逐次试验行为数据(请参见"材料和方法")。这种方法估算了所有参与者的组水平分布,这使我们能够对每个人的参数进行可靠的估算,而不会过拟合,并且可以使用抽样进行公平的模型比较。与之前的(8)一样,该模型捕获了参与者对高级信息的偏好(图1, H和I)。特别是,该模型定量地捕获了数据的关键特征,这是在较长的延迟条件下对即时信息的偏好增加(图1I)以及对概率条件的偏好(图S2)。我们还发现,除了奖励的正值外,参与者还为无奖励结果分配了负值,从而产生了与无结果相关的负期望效用(8)。如果参与者分配了较大的负值,这可以使模型避免提供高级信息[请参阅(8)以获取进一步的证据]。
其他标准模型没有捕获对高级信息的这种偏好。例如,具有折扣奖励但没有期望效用的模型,或者既具有折扣奖励又具有期望效用但没有期望增强的模型,无法捕获观察到的行为(请参见图S1进行说明)。我们通过使用层次贝叶斯方法将其他可能的模型拟合到行为数据来正式测试了这一点,并通过从组级别分布中进行采样比较了模型的集成贝叶斯信息标准(iBIC)得分(8)(请参阅"材料和方法")。这些分析强烈支持我们的完整模型优于其他标准计算模型(图S3)。
除了此处概述的任务行为外,我们的模型还捕获了与信息寻求行为有关的大量现有发现(3, 6, 25, 28),并可能与成瘾和赌博相关(8)(另请参见讨论)。然而,除了少数几个值得注意的例外[见(5)],描述神经相关性以期望获得未来奖励的丰富而复杂的文献令人印象深刻,这些文献主要集中在时间折扣的标准问题上。因此,如上所述,该文献没有涉及单独的和额外的提高的期望效用术语(有关详细信息,请参见"材料和方法"),该术语对解释与奖励有关的行为的广泛范围是必要的。
因此,我们接下来试图使用捕获参与者行为的计算模型来阐明预期产生的价值的神经生物学基础。特别是,我们模型的三个关键组成部分是令人感兴趣的:在等待期间的期望效用表示,高级信息提示呈现中的aRPE信号以及在惊喜之后的等待期间的持续预期信号。为了确定用于期望效用的唯一信号,我们对其他相关信号进行了回归分析,例如未来奖励的期望价值。最后,我们研究了编码这些计算组件的大脑区域如何耦合在一起以动态地协调期望效用,包括大脑如何将奖励信息的到达与期望效用联系起来。
重要的是要注意,我们的计算模型是一种通用的数学公式,没有指定期望效用的心理根源。这类似于标准强化学习模型,该模型包含了非常复杂的奖励价值心理根源(29)。我们的目标是阐明我们的计算模型的数学预测的神经相关性,即高级信息如何链接到期望期间产生的价值,进而驱动行为。在"讨论"中,我们讨论了期望效用的可能的心理根源。
The vmPFC encodes the utility of anticipation
我们的模型预测,期望信号发放会在整个延迟周期内动态变化("材料和方法"中的等式11)。不管增强如何,信号都会随着结果的接近而上升,但是该价值也受到常规折扣的影响。这意味着在典型的参数设置下,随着时间的推移会出现倾斜的倒U形(图2A)。
根据适合选择行为的层次模型,我们在计算模型中计算了每个参与者的最大后验(MAP)参数。 使用这些参数,我们估计了我们在神经数据上测试的几个变量的特定于对象的时程。 这些预测包括(i)等待期间的预期效用值(材料和方法中的方程11),(ii)相同等待期间的折旧结果值(标准期望值)(材料和方法中的方程13)和( iii)提示提示时的预测误差(材料和方法中的等式17)。这些信号与SPM(统计参数映射)默认规范HRF(血液动力学响应函数)进行卷积(图2B;示例参见图S5)。 如材料和方法中所述,我们将预测性预期信号分离为正向奖励和无向奖励,因为我们发现参与者将无奖励结果分配为负值(8)。 在整个数据分析中,针对参数回归器的SPM定向正交化已关闭。
请注意,以前对价值计算(包括时间差异学习)的研究都集中在预期未来奖励的当前价值上。 此数量通常与我们当前研究的重点紧密相关,即与未来奖励相关的额外预期效用(图S5)。因此,与预期效用相关的脑信号通常可以被分类为未来奖励的期望值的相关。 在这里,通过将这些回归变量包括在同一通用线性模型(GLM)中,我们可以为预期的效用确定唯一的相关性。 我们从分析中排除了等待时间短(1 s)的试验,以分离对线索响应的影响。
我们发现,模型的正向奖励预期效用信号与vmPFC中的血氧水平依赖性信号(BOLD)显着相关{P <0.05,全脑家族误差(FWE)校正; 蒙特利尔神经病学研究所(MNI)的峰值坐标[10,50,16],t = 6.02; 图2C}和尾状(P <0.05,全脑FWE校正;峰值坐标[-20,-2,18],t = 5.81;图S6)。 这些结果与先前在vmPFC(30,31)中报告的想象的奖励值以及在vmPFC(5,13,32)和尾状体(9)中报告的预期活动的表示形式相一致。 在整个大脑中,我们发现,在严格的全脑矫正后幸存下来的无报酬结果对预期效用没有显着影响(见图S7)。 因此,我们专注于预期效用。
考虑到在缓慢变化的信号中避免自相关潜在的误报的重要性(33),我们进行了非参数相位随机测试,在傅立叶分解中对信号的相位进行加扰(图S8A)(34、35)。 该测试可用于神经影像学和电生理学研究,从而避免假阳性发现,特别是在分析诸如值之类的慢信号之间的相关性时(33、35)。 为此,我们将模型针对每个参与者的预测预期效用信号转换为傅立叶空间,将每个频率分量的相位随机化,然后将信号转换回原始空间。 只有要测试的回归变量是随机的,而其他回归变量在完整的GLM中保持不变。 然后,我们对每个具有加扰信号的参与者的完整GLM进行了标准分析,然后进行了第二级分析。 通过多次重复此过程,我们创建了一个空分布。为了保护此测试免受家庭错误的影响,我们通过从我们的第二级分析的每一个分析中,获取感兴趣区域(ROI)或整个大脑的相关分数的最大值,从而构造了零分布。 原始分析中的相关值。 我们发现,在vmPFC(P <0.001,随机化全脑FWE校正)和尾状核(P <0.01,随机化全脑FWE校正)中的效果在此傅立叶相随机化测试中幸存下来(图S8B;另请参见 图S9)。
在等待期间,对这些信号的更详细检查显示,vmPFC活动的时间过程与我们模型的预测非常相似。 在图2D中,我们分别针对两个条件(即,当参与者收到奖励预测提示(红色)和当参与者收到否定提示)时,在等待期间分别绘制了图2C所示vmPFC群集中平均功能磁共振成像信号的时间过程。 -信息提示(洋红色)。 时间课程会跟踪每种情况(黑色)下模型的预测。
(未完待续,本节未完成翻译)
The dopaminergic midbrain encodes our computational model's aRPEs at the time of advanced information cues
The midbrain-hippocampus-vmPFC circuit implicates our model's predicted coupling of prediction error (at advanced information) to the utility of anticipation
DISCUSSION
MATERIALS AND METHODS
Participants
自伦敦大学学院(UCL)社区招募了39名自称异性恋的男性参与者(21)。参与者提供了参加研究的知情同意书,并获得了UCL伦理委员会的批准。
Experimental task
该任务是(8)中任务的变体,其本身是受一系列动物实验启发而寻求信息或观察行为的(例如(22, 25))。在每个试验的开始,都显示了一对任务信息刺激(沙漏和部分覆盖的人体轮廓)以及两个选择目标。沙漏上的数字表示参与者必须等待多长时间才能看到奖励或无奖励,其中1/2, 1, 2, 4和8的沙漏分别意味着等待时间为1, 5, 10, 20和40 s。另一个刺激是部分遮盖的人体轮廓,它表示看到奖励的概率,该奖励由未覆盖的半圆的面积指定(奖励的机会分别为5%, 25%, 50%, 75%和95%)。两个横向矩形目标被提出作为选择:被标记为"立即查找"的即时信息目标和被标记为"保持秘密"的无信息目标。在每个试验中,沙漏和被遮盖的轮廓的位置保持不变,但是在每个试验中,选择目标的位置在左右之间随机交替。
要求参与者在3 s内按下按钮在左右目标之间进行选择。一旦参与者选择了目标,三个提示之一就会出现在屏幕中央。如果参与者选择了即时信息目标,则提示即将奖励或无奖励的提示会出现在屏幕上,直到奖励或无奖励开始。如果参与者选择了无信息目标,则没有有关奖励信息的提示会出现在屏幕上。提示的含义已事先完全告知参与者。提示的含义在参与者之间是平衡的。为了确保立即消耗,奖励是来自一组先前被证实对异性恋男性参与者具有适当吸引力的女模特照片(8, 21);奖励图像呈现了1 s。图像是从(21)中介绍的前100张频率最高的图片中随机选择的。没有向同一参与者展示两次以上的图像。在没有奖励的情况下,会显示1 s表示没有奖励的图像。无论哪种情况,在开始新的试验之前,都会出现空白屏幕1 s。设置这些时序是为了减少时序不确定性,这可能会导致预测误差,从而可能会干扰我们模型的价值计算。
完整地指导了参与者有关任务结构的知识,包括有关概率和延迟条件的刺激含义,以及高级信息提示。然后,参与者接受了包括以下三个任务的广泛训练:可变延迟但固定概率任务,固定延迟但可变概率任务以及可变延迟和可变概率任务。这确保了参与者在扫描之前完全了解了任务并充分发展了偏好。扫描分为三个独立的运行,每个运行包含25个试验,一次覆盖所有条件。试验顺序在参与者之间随机分配。参与者在两次运行之间有大约30 s的休息时间。
Computational model
我们使用了(8)中描述的模型。简而言之,遵循Loewenstein的建议,对奖励的期望本身具有享乐价值(1, 2)(例如,参与者在等待奖励时喜欢思考奖励),我们扩展了标准强化学习框架,将显式的奖励期望包括在内,这通常被称为品味(1)。该模型的创新之处在于,可以通过与即将获得的奖励有关的高级信息相关的RPE来提高期望效用(8)。我们注意到,这里的品味是一个数学上定义的经济学术语,不同于在积极的心理学中(增强积极情绪的行为)(尽管可能与之相关)。
为了正式描述模型,请考虑一项任务,如果参与者选择即时信息目标,则他们在t = 0时会收到概率为q的奖励预测提示S+或概率为1 - q的无奖励预测提示S-。随后,受试者在t = T(= Tdelay)时分别获得R+或R-的奖励或无奖励。在我们最近的实验中,我们发现参与者为没有奖励而分配了负值(8),但这并没有必要考虑对在动物中观察到的高级信息的偏好(3, 25)。
根据观察者认为参与者倾向于延迟消耗某些类型的奖励的观点,Loewenstein建议参与者在等待奖励时提取效用(1, 2, 26)。形式上,在时间 t 上对未来奖励R+的期望值得a(t) = R+e−v+(T-t),其中v+决定其回报率。包括R本身,并考虑时间折扣,奖励预测提示Qs+的总价值为:
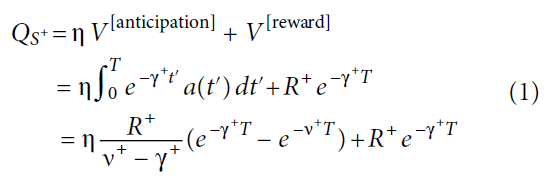
其中η是期望的相对权重,γ+是折扣率,T是延迟直到交付奖励为止的持续时间。在先前的工作中,η被视为一个常数,与受试者想象未来结果的能力有关(1);但是,我们提出它可以有所不同。调节的大小由预测提示时的δaRPE确定(8)。我们的建议是受到这样的暗示启发而发现的,这些发现大大激发了人们的兴奋感(25)。这种关系产生了一种简单的增强方式:
![]()
其中η0指定基本期望,C确定增益。在将我们的模型应用到相对不愉快的结果中,重要的是aRPE的绝对值会增强期望(8)。在整个等待期间,增强一直持续。
然后,无奖励预测提示的总价值QS-为:
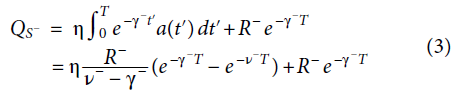
根据之前的工作,我们假设γ = γ+ = γ−。
aRPE影响总提示价值QS+和QS-,进而影响后续的aRPE。因此,通过aRPE(等式2)来增强期望的线性假设可能会由于无限制的增强而导致不稳定。这种不稳定性可以解释成瘾和赌博等不良适应行为。但是,在各种参数中,此假设具有稳定且自洽的解决方案。在我们的实验中,奖励和无奖励预测线索的aRPE可以表示为:
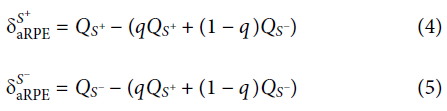
假定线性假设:
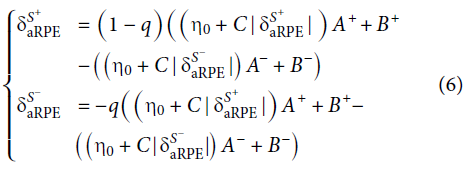
其中:
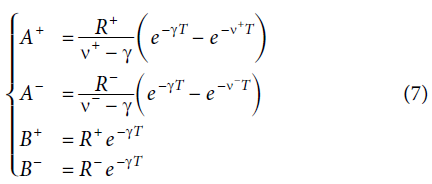
假设R-≤0且0≤R+,则 6表示that Sa R + PE> 0,aSR − PE <0。 6可以减少到:
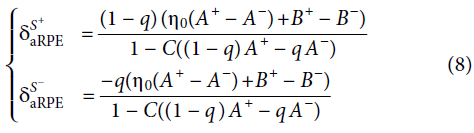
因为(η0(A+ - A-) + B+ - B-) > 0,对所有q和T,为了保持![]() 和
和![]() 成立,分母对于所有0 ≤ q ≤ 1和0 ≤ T都必须为正。换句话说:
成立,分母对于所有0 ≤ q ≤ 1和0 ≤ T都必须为正。换句话说:
![]()
对于0 ≤ q ≤ 1和0 ≤ T,或者![]() ,对于0 ≤ q ≤ 1和0 ≤ T。这意味着0 ≤ T时
,对于0 ≤ q ≤ 1和0 ≤ T。这意味着0 ≤ T时![]() 。直接表明A+在
。直接表明A+在![]() 时达到最大值,以及|A−|在
时达到最大值,以及|A−|在![]() 处。因此,线性假设给出稳定的自洽解的条件是:
处。因此,线性假设给出稳定的自洽解的条件是:
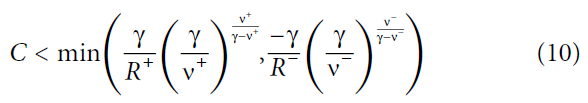
(未完待续)
Model's fMRI predictions (parametric and time-varying regressors)
Behavioral model fitting
Model comparison
fMRI data acquisition
fMRI data preprocessing
fMRI GLM analysis
Fourier phase-randomization test
Regions of interests
PPI analysis




 浙公网安备 33010602011771号
浙公网安备 33010602011771号