一阶低通滤波器（LPF）使用详讲
一阶低通滤波器（Low Pass Filter，LPF）的核心作用是：允许输入信号中频率低于设定截止频率的成分通过（衰减极小），阻隔或大幅衰减高于截止频率的高频噪声，从而获得更纯净的目标信号。
一、一阶低通滤波器定义
对于一阶低通滤波而言，从控制模型上分析就是一个一阶惯性环节，其描述形式如式所示：
\[H\left( s \right) =\frac{1}{Ts+1}
\]
\[\text{注：}T=\frac{1}{w_c}\text{，}w_c=2\pi \cdot f_c\text{；}
\text{其中，}T\text{为时间常数，}w_c\text{为角频率，}f_c\text{为截止频率}
\]
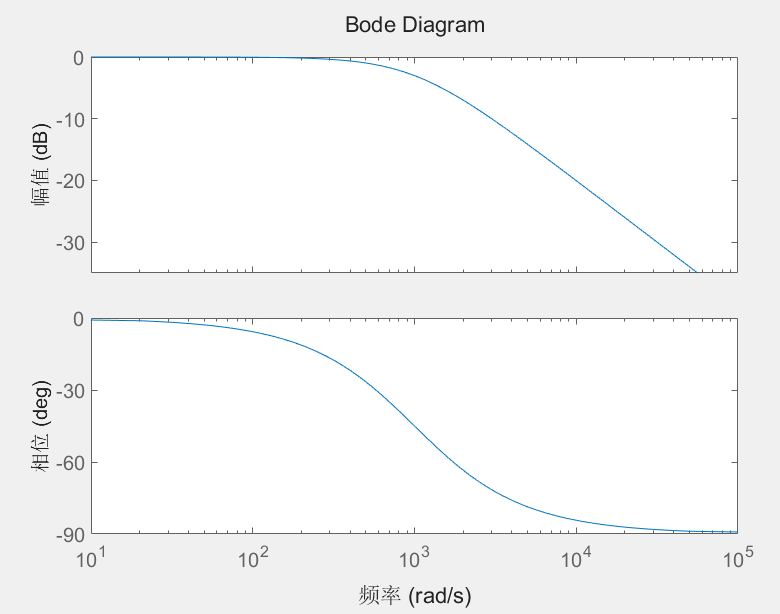
幅频响应：
\[\begin{equation}
|H(j\omega)| = \frac{1}{\sqrt{1+(\omega T)^2}} = \frac{1}{\sqrt{1+\left(\frac{\omega}{\omega_c}\right)^2}}
\end{equation}
\]
相频响应：
\[\begin{equation}
\angle H(j\omega) = -\arctan(\omega T) = -\arctan\left(\frac{\omega}{\omega_c}\right)
\end{equation}
\]
简单来说，一阶低通滤波器就做了一件事：让慢的变化通过，阻隔快的变化。 在实际工程中使用一阶低通滤波器时，需特别注意以下特点：
- 平滑效果：它能滤除高频噪声（如 ADC 抖动、电源纹波）。截止频率设得越低，对输入信号变化的响应越慢。
- 相位滞后：输出信号总是比输入信号“慢半拍”。在闭环控制系统（如 PID）中，如果滤波强度过大，会导致系统响应迟钝甚至震荡。
- 衰减特性：在截止频率
fc处，信号幅度衰减至-3dB（约为 0.707 倍），相位滞后-45°
滤波效果对比图如下：
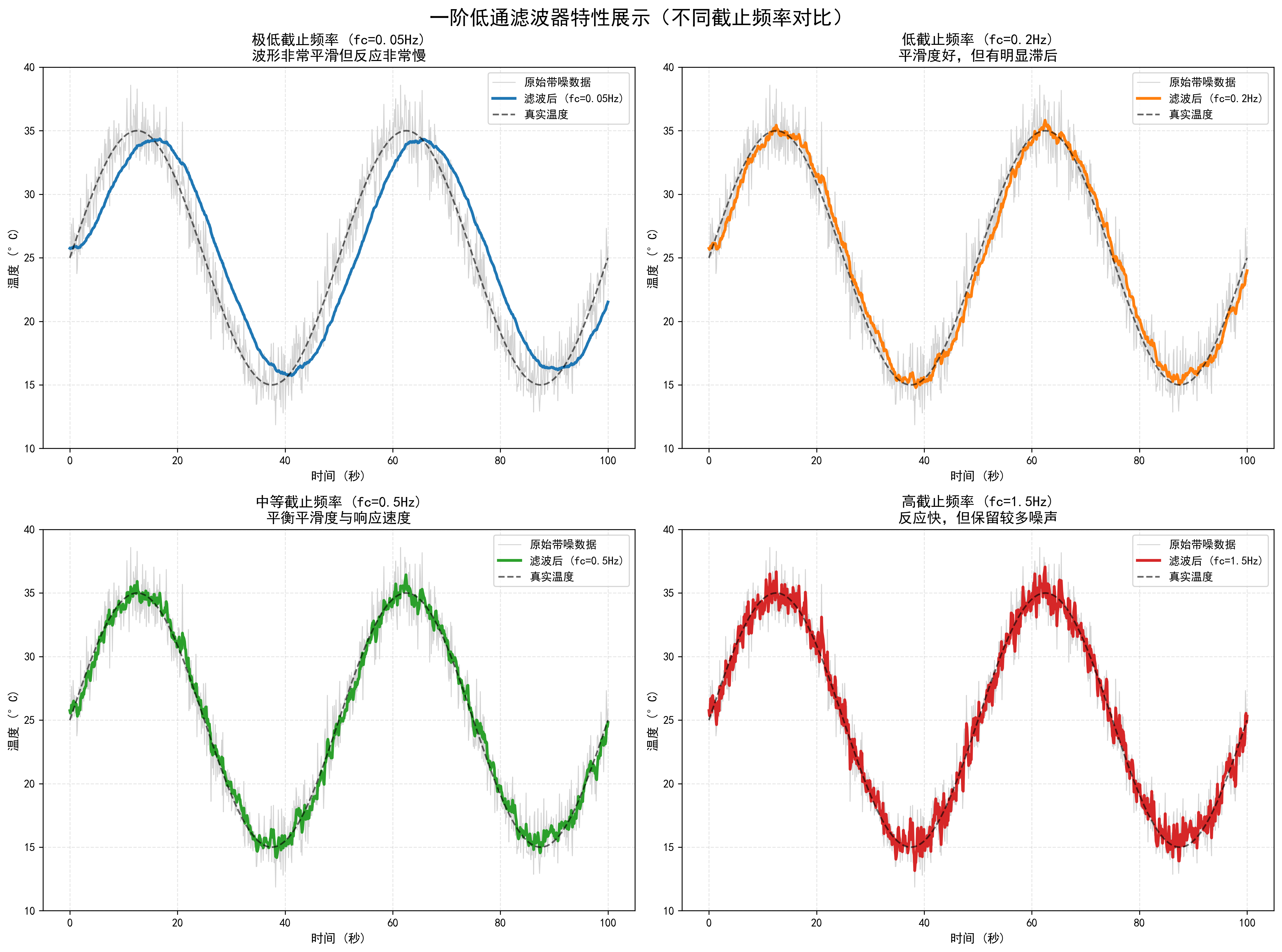
二、一阶低通滤波器的使用
在使用滤波器前，需厘清四个核心概念（以车载 IMU 为例）：
- 信号频率：车辆加速度的变化（你想测的，较慢）；
- 噪声频率：发动机的震动（你想滤的，较快）；
- 采样频率：你采集数据的频率（干活速度，必须足够快以看清噪声并滤除）；
- 截止频率：设定的“分界线”，应介于信号和噪声之间。
在实际工程中，我们设计滤波器主要有两个方向：
1、设计传感器（为了达到目标去选硬件）
这是自顶向下的设计思路。当我们明确了需要测量的信号和需要滤除的噪声时，反过来推算硬件需求。
- 确定范围：已知信号频率（如 5 Hz）和噪声频率（如 50 Hz）。
- 设定分界线：选择截止频率
fc介于二者之间（如 10 Hz）。 - 推算采样频率：为了保证数字滤波算法的准确性，工程上通常要求采样频率大于 10 倍的截止频率（经验值，确保滤波精度）。因此，我们需要选择采样频率至少为 100 Hz 的传感器。
2、使用传感器（有了硬件去调参数）
这是自底向上的调试思路。在硬件采样频率固定（如 IMU 锁定在 100 Hz）的情况下，寻找截止频率的最佳设置区间。
- 算上限：工程上通常要求采样频率大于 10 倍的截止频率（经验值，确保滤波精度），即截止频率小于 10 Hz。
- 看下限：为了保留有效信号，截止频率必须大于信号频率（如 5 Hz）。
- 定参数：在“上限”和“下限”的夹缝中选择一个值（如 8 Hz）。如果信号频率高于上限（如想测 50 Hz 震动），则说明该传感器采样频率不足，无法胜任。
三、C语言实现
使用以下代码，请包含以下公共内容
#include <stdint.h>
#include <math.h> /* 双线性变换法需要用到 tanf */
#ifndef PI
#define PI 3.14159265358979323846f
#endif
1、后向差分方法（Backward Difference）
这是最经典、最稳健的实现方式。它利用上一时刻的输出值进行递推，数值稳定性高，无条件稳定。适用于绝大多数传感器滤波、电机控制等通用场景。若调试中发现数据有明显的相位滞后，可适当增大截止频率。
#include <stdint.h> /* 推荐包含标准类型定义 */
/**
* @brief 后向差分法一阶低通滤波器结构体
*/
typedef struct
{
float alpha; /* 滤波系数 */
float one_minus_alpha; /* 预计算的 (1 - alpha) */
float last_output; /* 上一次滤波输出值 */
float cutoff_freq; /* 截止频率 */
float sample_freq; /* 采样频率 */
} LPF_BackwardEuler;
/**
* @brief 后向差分法一阶低通滤波器初始化函数
* @param filter : 滤波器结构体指针
* @param cutoff_freq : 截止频率
* @param sample_freq : 采样频率
* @retval 0:成功, -1:参数错误
* @note 建议 sample_freq 至少为 cutoff_freq 的 10 倍以获得较好的效果
*/
int lpf_backward_euler_init(LPF_BackwardEuler *filter, float cutoff_freq, float sample_freq)
{
if (filter == NULL || cutoff_freq <= 0.0f || sample_freq <= 0.0f)
{
return -1;
}
/*
* 限制采样率不得低于奈奎斯特频率 (2倍)，否则无法重构信号。
* 实际工程中为了滤波效果，通常建议 10 倍以上。
*/
if (sample_freq < 2.0f * cutoff_freq)
{
return -1;
}
float tau = 1.0f / (2.0f * PI * cutoff_freq);
float ts = 1.0f / sample_freq;
filter->alpha = ts / (tau + ts);
filter->one_minus_alpha = 1.0f - filter->alpha;
/* 初始化结构体成员 */
filter->cutoff_freq = cutoff_freq;
filter->sample_freq = sample_freq;
filter->last_output = 0.0f;
return 0;
}
/**
* @brief 后向差分法一阶低通滤波器计算函数
* @param filter : 滤波器结构体指针
* @param input : 当前输入值
* @retval 滤波后的输出值
*/
float lpf_backward_euler_update(LPF_BackwardEuler *filter, float input)
{
float output;
if (filter == NULL)
{
return input;
}
/* 核心公式：y[n] = alpha * x[n] + (1 - alpha) * y[n-1] */
output = filter->alpha * input + filter->one_minus_alpha * filter->last_output;
filter->last_output = output;
return output;
}
/**
* @brief 重置后向差分法一阶低通滤波器状态
* @param filter : 滤波器结构体指针
* @param init_val : 重置后的初始输出值
* @retval 0:成功, -1:参数错误
*/
int lpf_backward_euler_reset(LPF_BackwardEuler *filter, float init_val)
{
if (filter == NULL)
{
return -1;
}
filter->last_output = init_val;
return 0;
}
2、前向差分法（Forward Difference）
公式简单，但属于显式欧拉法，只有在特定情况下才稳定。由于对采样频率和截止频率的比例敏感，容易出现发散。除非有特殊的极低频需求或对代码极其简化，否则一般不推荐。
/**
* @brief 前向差分法一阶低通滤波器结构体
*/
typedef struct
{
float alpha; /* 滤波系数 (omega * Ts) */
float one_minus_alpha; /* 预计算的 (1 - alpha) */
float last_input; /* 上一次滤波输入值 x[n-1] */
float last_output; /* 上一次滤波输出值 y[n-1] */
float cutoff_freq; /* 截止频率 */
float sample_freq; /* 采样频率 */
} LPF_ForwardDifference;
/**
* @brief 前向差分法一阶低通滤波器初始化函数
* @param filter : 滤波器结构体指针
* @param cutoff_freq : 截止频率
* @param sample_freq : 采样频率
* @retval 0:成功, -1:参数错误
*/
int lpf_forward_difference_init(LPF_ForwardDifference *filter, float cutoff_freq, float sample_freq)
{
if (filter == NULL || cutoff_freq <= 0.0f || sample_freq <= 0.0f)
{
return -1;
}
/*
* 前向差分法虽然有理论稳定极限 (PI * fc)，但在接近极限时误差极大。
* 此处强制执行 10 倍规则，确保工程应用的可靠性。
*/
if (sample_freq < 10.0f * cutoff_freq)
{
return -1;
}
/* 计算过程系数 */
float tau = 1.0f / (2.0f * PI * cutoff_freq);
float ts = 1.0f / sample_freq;
filter->alpha = ts / tau;
filter->one_minus_alpha = 1.0f - filter->alpha;
/* 初始化结构体成员 */
filter->cutoff_freq = cutoff_freq;
filter->sample_freq = sample_freq;
filter->last_input = 0.0f;
filter->last_output = 0.0f;
return 0;
}
/**
* @brief 前向差分法一阶低通滤波器计算函数
* @param filter : 滤波器结构体指针
* @param input : 当前输入值
* @retval 滤波后的输出值
*/
float lpf_forward_difference_update(LPF_ForwardDifference *filter, float input)
{
float output;
if (filter == NULL)
{
return input;
}
/* y[n] = (1 - Ts/Tau)y[n-1] + (Ts/Tau)x[n-1] */
output = filter->one_minus_alpha * filter->last_output + filter->alpha * filter->last_input;
/* 更新历史值：当前输入作为下一次的历史输入 */
filter->last_input = input;
filter->last_output = output;
return output;
}
/**
* @brief 重置前向差分法一阶低通滤波器状态
* @param filter : 滤波器结构体指针
* @param init_val : 重置后的初始输出值
* @retval 0:成功, -1:参数错误
*/
int lpf_forward_difference_reset(LPF_ForwardDifference *filter, float init_val)
{
if (filter == NULL)
{
return -1;
}
filter->last_input = init_val;
filter->last_output = init_val;
return 0;
}
3、双线性变换法（Tustin / Bilinear）
通过双线性变换将模拟域映射到数字域。它不仅能利用当前输入，还利用了历史输入和输出，其频率响应特性最接近理论模拟滤波器。适用于对幅频特性要求较高的音频处理、信号分析，或采样频率相对较低的精密控制场合。
/**
* @brief 双线性变换法一阶低通滤波器结构体
*/
typedef struct
{
float b0; /* 输入系数 b0 */
float b1; /* 输入系数 b1 */
float a1; /* 反馈系数 a1 */
float last_input; /* 上一次滤波输入值 x[n-1] */
float last_output; /* 上一次滤波输出值 y[n-1] */
float cutoff_freq; /* 截止频率 */
float sample_freq; /* 采样频率 */
} LPF_BilinearTransform;
/**
* @brief 双线性变换法一阶低通滤波器初始化函数
* @param filter : 滤波器结构体指针
* @param cutoff_freq : 截止频率
* @param sample_freq : 采样频率
* @retval 0:成功, -1:参数错误
*/
int lpf_bilinear_transform_init(LPF_BilinearTransform *filter, float cutoff_freq, float sample_freq)
{
if (filter == NULL || cutoff_freq <= 0.0f || sample_freq <= 0.0f)
{
return -1;
}
/* 奈奎斯特频率限制 */
if (sample_freq < 2.0f * cutoff_freq)
{
return -1;
}
float wc = 2.0f * PI * cutoff_freq;
float T = 1.0f / sample_freq;
/* 频率预扭曲，目的是消除双线性变换在高频处的非线性频率畸变，确保截止频率准确 */
float wc_twisted = (2.0f / T) * tanf((wc * T) / 2.0f);
/* 计算双线性变换系数 */
float K = (wc_twisted * T) / 2.0f;
float denominator = 1.0f + K;
filter->b0 = K / denominator;
filter->b1 = filter->b0;
filter->a1 = (K - 1.0f) / denominator;
/* 初始化结构体成员 */
filter->cutoff_freq = cutoff_freq;
filter->sample_freq = sample_freq;
filter->last_input = 0.0f;
filter->last_output = 0.0f;
return 0;
}
/**
* @brief 双线性变换法一阶低通滤波器计算函数
* @param filter : 滤波器结构体指针
* @param input : 当前输入值
* @retval 滤波后的输出值
*/
float lpf_bilinear_transform_update(LPF_BilinearTransform *filter, float input)
{
float output;
if (filter == NULL)
{
return input;
}
/* 核心公式：y[n] = b0*x[n] + b1*x[n-1] - a1*y[n-1] */
output = filter->b0 * input
+ filter->b1 * filter->last_input
- filter->a1 * filter->last_output;
/* 更新历史状态 */
filter->last_input = input;
filter->last_output = output;
return output;
}
/**
* @brief 重置双线性变换法一阶低通滤波器状态
* @param filter : 滤波器结构体指针
* @param init_val : 重置后的初始输出值
* @retval 0:成功, -1:参数错误
*/
int lpf_bilinear_transform_reset(LPF_BilinearTransform *filter, float init_val)
{
if (filter == NULL)
{
return -1;
}
filter->last_input = init_val;
filter->last_output = init_val;
return 0;
}
4、工程选择速查表
| 方法 | 稳定性 | 计算量 | 相位/延迟特性 | 核心特点 | 适用场景 |
|---|---|---|---|---|---|
| 后向差分法 | 无条件稳定 | 极低 (1次乘法 + 1次乘加) | 存在相位滞后 (隐式欧拉) | 最常用，最稳健。系数计算简单，不涉及三角函数。 | 绝大多数场景。 电机控制、传感器去噪、PID滤波。 |
| 双线性变换法 | 无条件稳定 | 中等 ( 3 次乘加) | 频率响应最准 (需预扭曲) | 精度最高。在截止频率处的幅值衰减最准确（-3dB），频率映射保真度最好。 | 高精度要求。 音频处理、精密仪器、精密测量、电源闭环控制。 |
| 前向差分法 | 有条件稳定 (需 fs > π·fc) | 极低 | 延迟最大 (显式，多拍滞后) | 算法简单，但天然引入 1 个采样周期的纯延迟，且易发散。 | 极少推荐。 仅在处理极低频信号且计算资源极其受限时考虑。 |
四、总结
一阶低通滤波器是嵌入式信号处理中最基础、最常用的工具。正确使用它的关键，在于理解信号频率、噪声频率、采样频率与截止频率之间的制约关系。在实际开发中，建议优先采用后向差分法进行实现，根据实际的采样频率和信号带宽，灵活调整截止频率，以达到去噪与响应速度的最佳平衡。
浙公网安备 33010602011771号