压缩感知:一种新型亚采样技术
绿蚁新醅酒,红泥小火炉。晚来天欲雪,能饮一杯无?
[导读] 压缩感知(Compressed Sensing, CS)是近些年提出来的一种亚采样技术,其采样率远小于传统的奈奎斯特采样定理所需要的采样数,后者需要以不低于2倍信号的最高频率对信号进行采样才能完美重构原信息,而CS技术只需极少量的采样即可精确重建原始信号。2006年,David.L. Donoho和著名的华人数学天才、菲尔兹奖得主陶哲轩等人对CS理论进行了严格证明,搭建了完整的理论框架,自此以后,CS技术在信号处理、图像处理、通信、自动控制、人工智能等领域得到了广泛的研究与应用。压缩感知的研究内容主要可以分为三个部分,即信号的稀疏表示、测量矩阵的构造和重构算法。其中,重构算法作为CS技术的关键之一,影响着信号的重构复杂度和重构质量。接下来的几期,将为大家带来每种类别中最经典的压缩感知重构算法,并附上仿真代码和详细解说。同时,也欢迎各位亲爱的读者朋友们在后台留言,与作者互动讨论。
———————————————————————————————————————————————
更多精彩内容请关注微信公众号 “优化与算法”
1. 信号的稀疏表示
对于\(N\)维的信号\(f\),可以表示为一组正交基向量\({\bf{ \Psi }}\)的线性组合:
其中\({\bf{\Psi }} \in {^{N \times N}}\)称为稀疏基,\({\bf{x}} \in {^{N \times 1}}\)为\(f\)在\(\bf \Psi\) 变换域中的系数向量,如果\(x\)中只有\(s\)(\(s \ll N\))个元素不为零(或远大于零,而其他元素接近于零),则称\(x\)是\(s\)-稀疏的。
信号的稀疏表示如图1所示
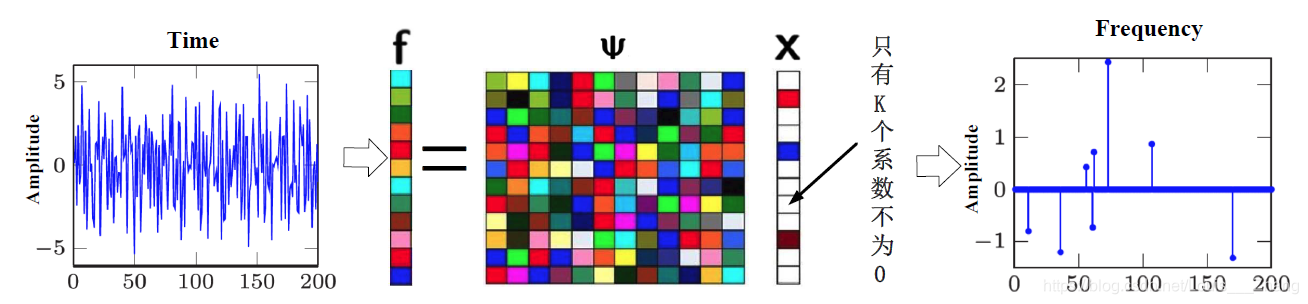
图1 信号的稀疏表示
2. 信号的压缩采样(测量矩阵的构造)
用一个\(M \times N(M < N)\)的测量矩阵\({\bf{\Phi }}\)对原信号\(f\)进行压缩采样,得到一个观测向量 \({\bf{y}} \in {^{M \times 1}}\),实现原信号的降维,此过程可以表示为:
其中\({\bf{A}} \in {^{M \times N}}\)称为观测向量。对具体问题而言,\({\bf{\Phi }}\)和\({\bf{\Psi }}\)为已知,因此\({\bf{A}}\) 也已知,从而可以通过观测向量\({\bf{y}}\)求得系数向量\({\bf{x}}\),然后再重构出原信号 。常用的测量矩阵有随机高斯矩阵,随机伯努利矩阵,及其他随机矩阵。
信号的压缩采样过程可以描述为图2:

3. 重构算法
由于\(M < N\),(2)式是一个欠定方程,因此直接求解此方程是一个NP-hard问题。文献[6]证明了当系数向量 是\(s\)-稀疏且满足\(s\)阶有限等距性质(Restricted isometry property, RIP)时,能以很高的概率精确求得 \({\bf{x}}\),然后通过式(1)求得原信号。求解过程等价于求解如下优化问题:
求解(3)式的过程称为信号的重建,信号的重建算法是压缩感知的关键问题之一,目前压缩感知重构算法主要可以分为基于\({\ell _0}\)范数的贪婪算法、基于\({\ell _1}\)范数的凸优化算法和组合算法等类别。
经典的重构算法罗列如下:
- 基于\({\ell _0}\)范数的贪婪算法:
- 匹配追踪算法(Matching Pursuit, MP)
- 正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)
- 正则化OMP算法(Regularized Orthogonal Matching Pursuit, ROMP)
- 压缩采样匹配追踪算法(Compressive Sampling Matching Pursuit CoSaMP)
- 子空间追踪算法(Subspace pursuit, SP)
- 分段正交匹配追踪算法
- 广义正交匹配追踪算法(Generalized Orthogonal Matching Pursuit, GOMP)
- ......
- 基于\({\ell _1}\)范数的凸松弛算法
- 基追踪(Basis Pursuit,BP)
- 基追踪降噪(Basis Pursuit DE-NOISING,BPDN)
- 最小角回归(Least Angle Regression,LAS)
- 近似消息传递(Approximate Message Passing,AMP)
- 迭代软阈值算法(Iterative Shrinkage Thresholding Algorithm, ISTA)
- 加速迭代软阈值算法(Fast Iterative Shrinkage Thresholding Algorithm, FISTA)
- ......
- 迭代硬阈值类算法
- 迭代硬阈值算法(Iterative Hard Thresholding, IHT)
- 正规化迭代硬阈值算法(Normalized Iterative Hard Thresholding, NIHT)
- 加速迭代硬阈值算法(Accelerated Iterative Hard Thresholding, AIHT)
- 共轭梯度迭代硬阈值算法(Conjugate Gradient Iterative Hard Thresholding, CGIHT)
- 基于回溯的迭代硬阈值迭代算法(Backtracking based Iterative Hard Thresholding, BIHT)
- 基于回溯的共轭梯度迭代硬阈值迭代算法(Conjugate Gradient based Backtracking Iterative Hard Thresholding, BIHT)
- ......
- 非凸优化算法
- 贝叶斯压缩感知(Bayesian Compressive Sensing,BCS)
- Focal Underdetermined System Solution (FOCUSS)
- Iterative Reweighted Least Squares (IRLS)
- ......
CS重构算法分类树见图3

参考PPT
本文部分内容参考下列slide:
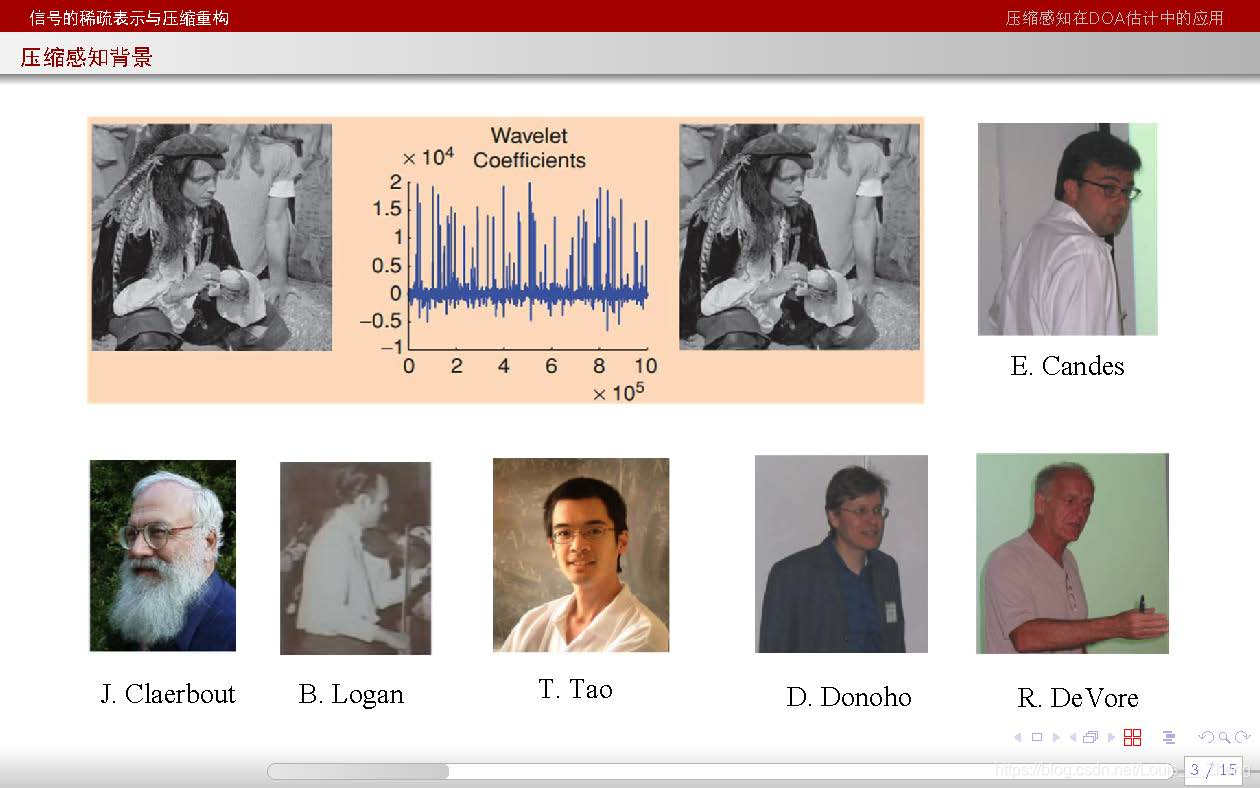

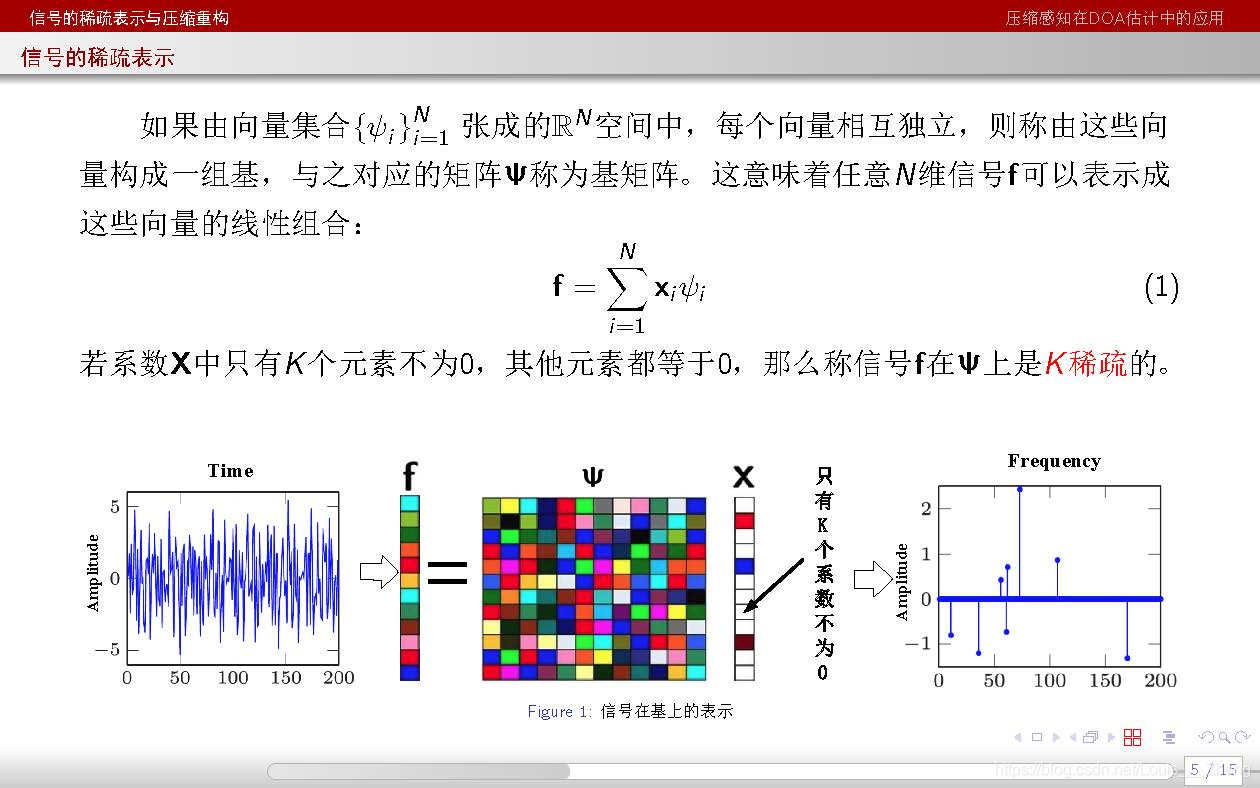


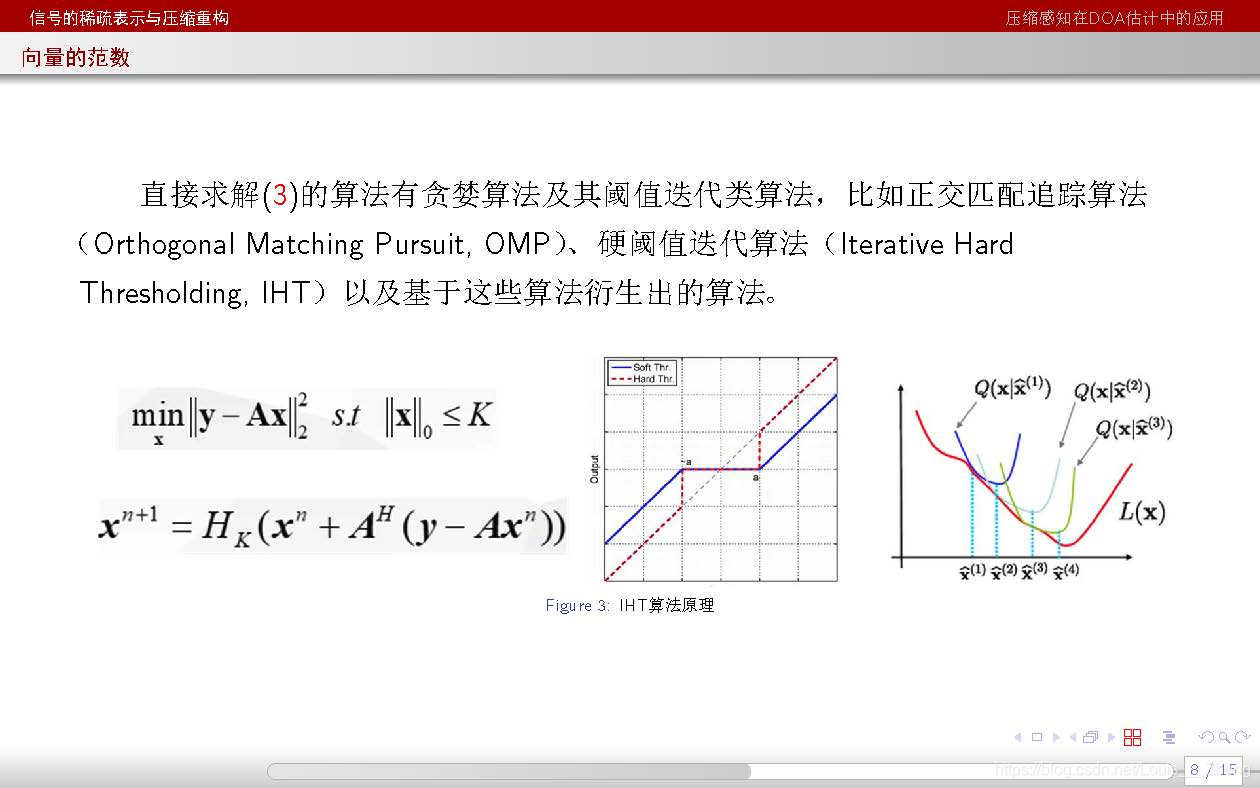
参考文献
[1] Donoho, David L. "Compressed sensing." IEEE Transactions on information theory 52.4 (2006): 1289-1306.
[2] 张雁峰, 范西岸, 尹志益, 等. 基于回溯的共轭梯度迭代硬阈值重构算法[J]. 计算机应用, 2018: 0-0.
[3] Zhang Y, Huang Y, Li H, et al. Conjugate Gradient Hard Thresholding Pursuit Algorithm for Sparse Signal Recovery[J]. Algorithms, 2019, 12(2): 36.
[4] Marques E C, Maciel N, Naviner L, et al. A review of sparse recovery algorithms[J]. IEEE Access, 2018, 7: 1300-1322.
更多精彩内容请关注微信公众号 “优化与算法”



 浙公网安备 33010602011771号
浙公网安备 33010602011771号