[算法 - FPGA] 带符号整数乘法器 (Verilog)

转自： https://blog.csdn.net/xszxyll/article/details/140279592

1.设计思路
本文主要讲解带符号整数乘法器设计思路，以及verilog电路实现 。

1.1 补码表示
有符号数表示都是使用补码表示，我们都知道，正数的补码是它本身，负数的补码是对应正数取法加一。对于一个4bit整数，如果表示无符号整数，它的范围是0-15；如果表示有符号整数。它的范围是-8到7。

1.2 乘法器设计思路
根据上表，可以得到对于两个4bit带符号数 A4 = a3a2a1a0，B4 = b3b2b1b0

A4 = -a3*2^3 + a2*2^2 + a1*2^1 + a0*2^0 例：A4 = 4'b1111 = -8 + 4 + 2 + 1 = -1

B4 = -b3*2^3 + b2*2^2 + b1*2^1 + b0*2^0 例：B4 = 4‘b1010 = -8 + 0 + 2 + 0 = -6

根据上面化简关系，A4 = -a3*2^3 + A3,

其中，A3可以表示为使用低三位表示的无符号整数 A3=a2a1a0。

由此，可以推导出如下表达式：

A4*B4 = (-a3*2^3  +A3)  *(-b3*2^3 + B3) = a3b3*2^6 - a3B3*2^3 - b3A3*2^3 + A3B3

A3B3 = (a2a1a0) * (b2b1b0)

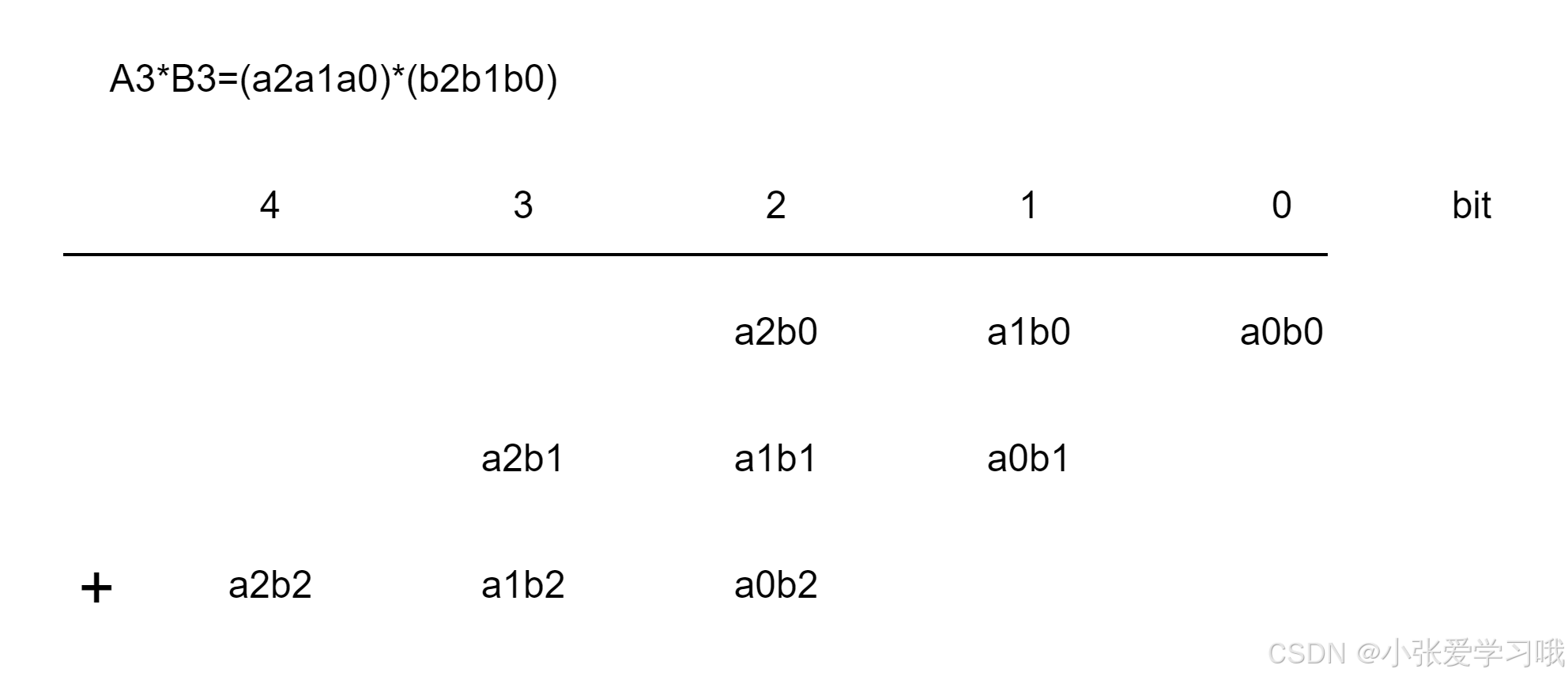
a3 B3 *2^3 =a3 (b2b1b0) * 2^3，这里乘2^3可以理解为左移3位

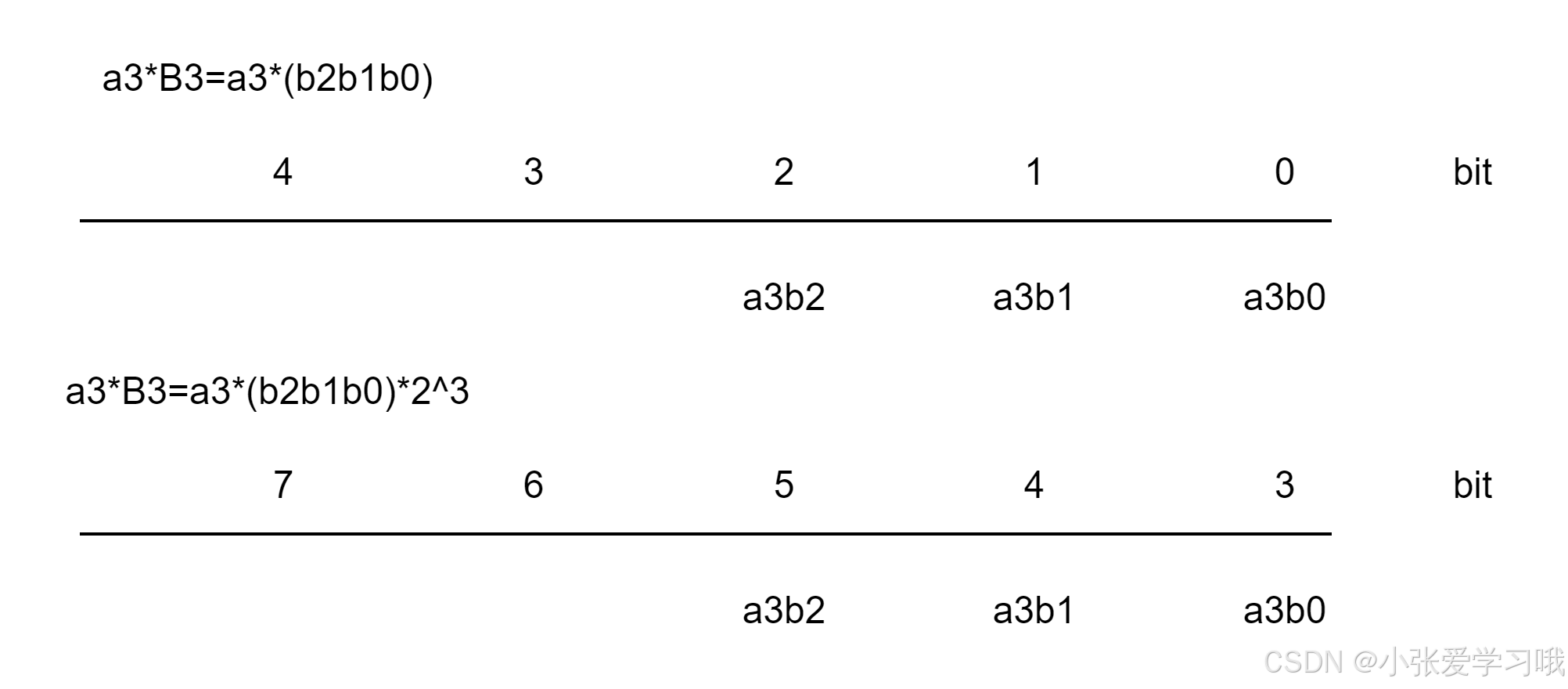
同理，计算 b3 A3 * 2^3

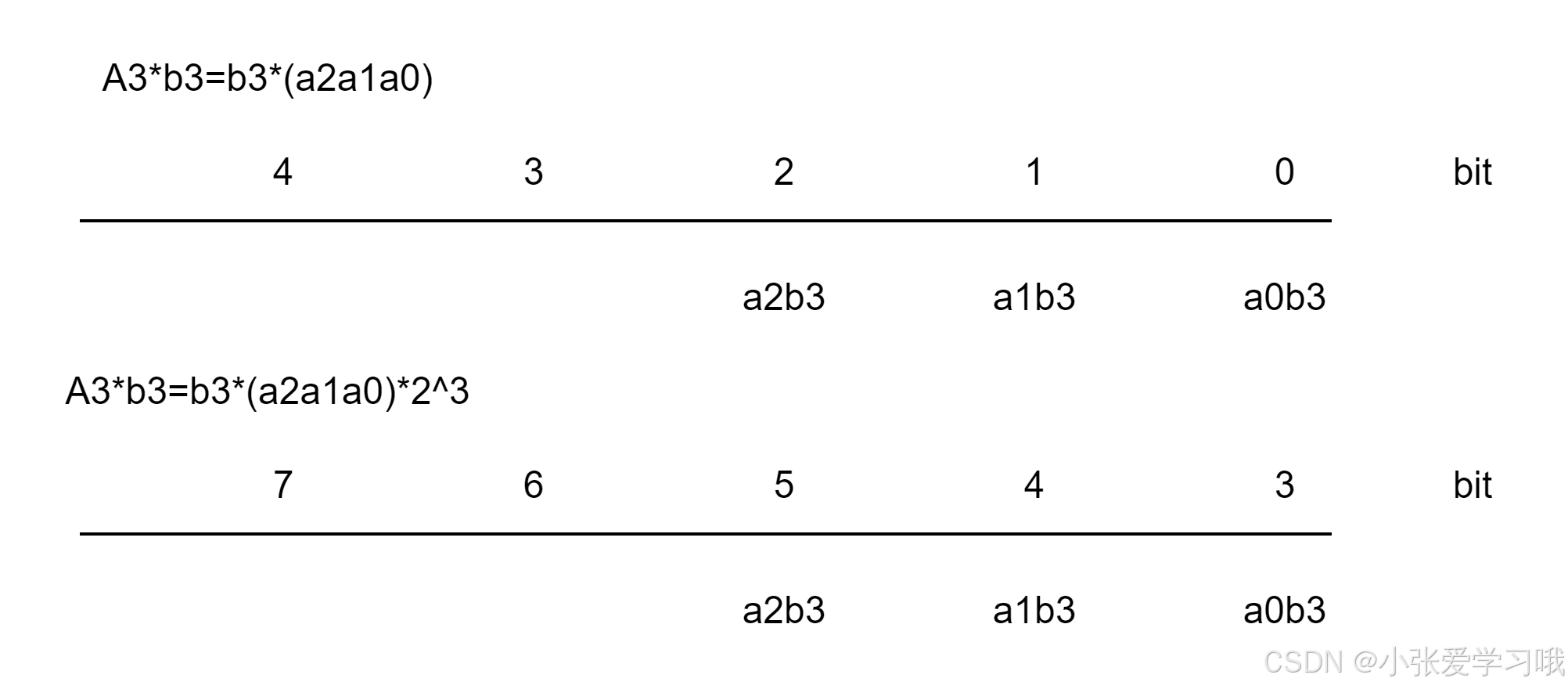
对  - a3B3*2^3 - b3A3*2^3 重新整理，可以得到（-a3B3 - b3A3)*2^3,再利用 -x = ~x+1（~表示取反）得到如下图：

将上述几个图的结果相加，推到最终可以得到如下结果：

2.电路实现

`timescale 1ns/1ps
 
module signed_mul 
#(
    parameter    DATA_LEN = 8 
)
(
    input  [ DATA_LEN -1   : 0 ] signed_mul_a_i    ,
    input  [ DATA_LEN -1   : 0 ] signed_mul_b_i    ,
 
    output [ DATA_LEN*2 -1 : 0 ] signed_mul_s_o    
);
 
wire [ DATA_LEN -1 : 0 ] a_bi [ DATA_LEN -1 : 0 ] ;
 
//-----------------------------------------------------------------------
//----每一行计算
//-----------------------------------------------------------------------
generate
    genvar i ;
    genvar j ;
 
    //AB
    for( i=0 ; i < DATA_LEN - 1 ; i=i+1 )begin
        for( j=0 ; j < DATA_LEN - 1 ; j=j+1)begin
            assign a_bi[i][j] = signed_mul_a_i[i] & signed_mul_b_i[j] ;
        end
    end
 
    //A4*B4 = (-a3*2^3 + A3) * (-b3*2^3 + B3) = a3b3*x^6 -a3B3*2^3 -A3b3*2^3 + A3B3 
    //aB
    for( i=0 ; i < DATA_LEN - 1 ; i=i+1 )begin
        assign a_bi[i][DATA_LEN - 1] = ~(signed_mul_a_i[DATA_LEN - 1] & signed_mul_b_i[i]) ;
    end
 
    //Ab
    for( i=0 ; i < DATA_LEN - 1 ; i=i+1 )begin
        assign a_bi[DATA_LEN - 1][i] = ~(signed_mul_a_i[i] & signed_mul_b_i[DATA_LEN - 1]) ;
    end
 
    //ab
    assign a_bi[DATA_LEN - 1][DATA_LEN - 1] = signed_mul_a_i[DATA_LEN - 1] & signed_mul_b_i[DATA_LEN - 1] ;
 
endgenerate
 
//-----------------------------------------------------------------------
//----求和
//-----------------------------------------------------------------------
wire [DATA_LEN*2 -1 : 0]add_sum[DATA_LEN -1 : 0];
 
generate
    genvar k ;
 
    assign add_sum[0] = {1'b1 , a_bi[0][DATA_LEN - 1] , a_bi[0][DATA_LEN - 2 : 0]} ;
    for( k=1 ; k<DATA_LEN-1 ; k=k+1 )begin
        assign add_sum[k] = { a_bi[k][DATA_LEN - 1] , a_bi[k][DATA_LEN - 2 : 0] } << k ;
    end
    assign add_sum[DATA_LEN - 1] = { 1'b1 , a_bi[DATA_LEN - 1][DATA_LEN - 1] , a_bi[DATA_LEN - 1][DATA_LEN - 2 : 0] } << (DATA_LEN - 1) ;
 
endgenerate
 
//根据实际多少位需要自己添加  可以使用类似于累加器  但是循环好像并不好写
assign signed_mul_s_o = add_sum[0] + add_sum[1] + add_sum[2] + add_sum[3] +
                        add_sum[4] + add_sum[5] + add_sum[6] + add_sum[7]   ;
 
endmodule //signed_mul

 

3.仿真验证

3.1验证代码

`timescale 1ns/1ps
 
module signed_mul_tb;
 
// Parameters
localparam  DATA_LEN = 8;
 
//Ports
reg [ DATA_LEN -1   : 0 ] signed_mul_a_i;
reg [ DATA_LEN -1   : 0 ] signed_mul_b_i;
wire [ DATA_LEN*2 -1 : 0 ] signed_mul_s_o;
 
signed_mul # (
    .DATA_LEN(DATA_LEN)
  )
  signed_mul_inst (
    .signed_mul_a_i(signed_mul_a_i),
    .signed_mul_b_i(signed_mul_b_i),
    .signed_mul_s_o(signed_mul_s_o)
);
 
integer i;
integer j;
 
initial begin
    signed_mul_a_i = 8'hff ;
    signed_mul_b_i = 8'hff ;
    #40;
    signed_mul_a_i = 8'h1  ;
    signed_mul_b_i = 8'hff ;
    #40;
    for(i=0 ; i<256 ; i=i+1 )begin
        for(j=0 ; j<256 ; j=j+1)begin
            signed_mul_a_i = i ;
            signed_mul_b_i = j ;
            #20 ;
        end
    end
 
    #100;
    $stop;
end
 
endmodule

 

3.2 验证结果