数据结构
数据结构
栈
- 栈,一种基本的先进后出的线性数据结构,手写栈一般有一个指针指向栈顶元素。
STL中有个容器叫stack,支持一些功能
- push,将元素放置在栈顶;
- top(),输出栈顶元素
- pop(),弹出栈顶元素
- size(),访问栈中元素
- clear,清空
详细操作可以见栈
手写栈
- 可以用数组模拟栈,代码如下。
int t=0;
struct sta{
int a[20100];
void push(int x){ a[++t]=x; }
void pop(){ --t; }
int top() { return a[t];}
int empty(int x){ return t==0?1:0;}
int size(){ return t;}
}st;
单调栈
- 单调栈即满足单调性的栈结构
- 可以用来维护左边或右边第一个比自己小或者大的
- 通过维护一个栈,如果比当前值小就弹出。
for(int i=n;i>=1;i--){
while(st.size()&&(a[st.top()]<=a[i])){
st.pop();
}
if(st.size()){
ans[i]=st.top();
}
st.push(i);
}
例题:
- 读题得到能匹配的就输出
- 不能匹配就填上
#include<bits/stdc++.h>
#include<stack>
using namespace std;
char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48),ch=getchar();}
return x*f;
}
inline void write(int x){
if(x<0)putchar('-'),x=-x;
if(x>9)write(x/10);
putchar(x%10+'0');
}
string s;
stack<pair<int,int> >st;
int vis[210];
signed main(){
cin>>s;
for(int i=0;i<s.size();i++){
if(s[i]=='('){
st.push(make_pair(i,0));
}
else if(s[i]=='['){
st.push(make_pair(i,1));
}
if(s[i]==')'&&st.size()){
if(st.top().second==0){
vis[st.top().first]=1;
vis[i]=1;
st.pop();
}
}
else if(s[i]==']'&&st.size()){
if(st.top().second==1){
vis[st.top().first]=1;
vis[i]=1; st.pop();
}
}
}
for(int i=0;i<s.size();i++){
if(vis[i]){
cout<<s[i];
}
else{
if((s[i]=='(')||(s[i]==')')){
cout<<"()";
}
else if((s[i]=='[')||(s[i]==']')){
cout<<"[]";
}
}
}
return 0;
}
队列
- 队列,是一种先进先出的线性数据结构,手写队列一般有两个指针指向队头和队尾元素
- 其对应 STL: queue
- 先进先出。
普通队列
- STL 即可
优先队列
- 也是二叉堆,可以维护最小/最大值。
- priority_queue
例题:
- 首先将相邻的放入优先队列,然后再从绝对值最小的开始出队,然后再将他们的位置用链表更新
#include<bits/stdc++.h>
#define mp make_pair
#define int long long
using namespace std;
int n;
string s;
int a[200010];
int nxt[200010],pre[200010];
int b[2000010];
struct node{
int sum,l,r;
};
bool operator<(node a,node b){
if(a.sum==b.sum)return a.l>b.l;
return a.sum>b.sum;
}
bool flag[200010];
priority_queue<node>q;
vector<pair<int,int> >st;
signed main(){
cin>>n;
cin>>s;s=" "+s;
for(int i=1;i<=n;i++){
cin>>a[i];
pre[i]=i-1;nxt[i]=i+1;
}
for(int i=1;i<=n;i++){
b[i]=(s[i]=='B');
}
for(int i=1;i<n;i++){
if(b[i]^b[i+1]) q.push((node){abs(a[i+1]-a[i]),i,i+1});
}
while(q.size()){
node t=q.top();
q.pop();
if((!flag[t.l])&&(!flag[t.r])){
flag[t.l]=1,flag[t.r]=1;
pre[nxt[t.r]]=pre[t.l];
nxt[pre[t.l]]=nxt[t.r];
st.push_back(mp(t.l,t.r));
if(pre[t.l]<1||nxt[t.r]>n) continue;
if(b[pre[t.l]]^b[nxt[t.r]]) q.push((node){abs(a[pre[t.l]]-a[nxt[t.r]]),pre[t.l],nxt[t.r]});
}
}
cout<<st.size()<<'\n';
for(int i=0;i<st.size();i++){
cout<<st[i].first<<" "<<st[i].second<<'\n';
}
return 0;
}
建筑抢修
- 读题得到意思是要我们尽量修最多的,而不修的一定是耗时最多的,这样会影响后面所有的
- 所以考虑先将截止时间排序,然后尝试放,如果放不了,那么就把耗时最大的弹出
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
struct node{
int t1,t2;
}a[150010];
priority_queue<int>q;
bool cmp(node x,node y){
if(x.t2!=y.t2) return x.t2<y.t2;
return x.t1<y.t1;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].t1>>a[i].t2;
}
sort(a+1,a+1+n,cmp);
int ans=0,sum=0;
for(int i=1;i<=n;i++){
ans+=a[i].t1;
q.push(a[i].t1);
if(ans<=a[i].t2){
sum++;
}
else{
ans-=q.top();
q.pop();
}
}
cout<<sum;
return 0;
}
ST表
- 可以静态维护区间问题,区间RMQ,区间GCD
- 通过倍增的方法维护。
具体实现如下
- 首先ST表维护一个数组st[i][j]表示从 \(i\) 的位置到 \(i+2^j\) 的区间问题
- 当前位置跳 \(2^j\) 等价于 先跳 \(2^{j-1}\) ,再跳 \(2^{j-1}\)
for(int j=1;j<=lg[n];j++){
for(int i=1;i<=n-(1<<j)+1;i++){
dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
}
查询
当前长度最大从l跳 \(2^j\) 不跳出去有多长,j是lg[len]。
cout<<max(dp[l][lg[len]],dp[r-(1<<lg[len])+1][lg[len]])<<'\n';
例题:
Max GEQ Sum
- 读题得到最大值得取值只有n种,考虑枚举最大值,然后用单调栈得到最左端和最右端得端点
- 因为我们想要区间和最大,即 \(pre[r]-pre[l-1]\) 最大,所以用ST表维护这个区间最大前缀和再处理即可
#include<bits/stdc++.h>
#define int long long
using namespace std;
long long T,n,a[200010],ans[200010],num[200100];
long long sum[200010];
long long dp[200010][30],dp1[200010][30],lg[200010];
stack<long long>q;
int qd(int l,int r){
int len=lg[r-l+1];
return max(dp[l][len],dp[r-(1<<len)+1][len]);
}
int qx(int l,int r){
int len=lg[r-l+1];
return min(dp1[l][len],dp1[r-(1<<len)+1][len]);
}
void init(){
for(int i=n;i>=1;i--){
while(!q.empty()&&a[i]>=a[q.top()]){
q.pop();
}
if(!q.empty()){
ans[i]=q.top()-1;
}
else{
ans[i]=n;
}
q.push(i);
}
while(q.size())
q.pop();
for(int i=1;i<=n;i++){
while(!q.empty()&&a[i]>=a[q.top()]){
q.pop();
}
if(!q.empty()){
num[i]=q.top()+1;
}
else{
num[i]=1;
}
q.push(i);
}
while(q.size())
q.pop();
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin>>T;
while(T--){
cin>>n;
lg[0]=-1;
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=sum[i-1]+a[i];
lg[i]=lg[i/2]+1;
}
for(int j=1;j<=lg[n];j++){
for(int i=0;i+(1<<(j-1))<=n;i++){
dp1[i][j]=1e9;
}
}
init();
for(int i=1;i<=n;i++){
dp[i][0]=sum[i];
dp1[i][0]=sum[i];
}
for(int j=1;j<=lg[n];j++){
for(int i=0;i+(1<<(j-1))<=n;i++){
dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
dp1[i][j]=min(dp1[i][j-1],dp1[i+(1<<(j-1))][j-1]);
}
}
bool flag=0;
for(int i=1;i<=n;i++){
int maxn=qd(i,ans[i]);
int minn=qx(num[i]-1,i-1);
// cout<<maxn<<" "<<minn<<"\n";
if(maxn-minn>a[i]){
flag=1;
cout<<"NO"<<"\n";
break;
}
}
// cout<<"\n";
if(!flag)
cout<<"YES"<<"\n";
}
return 0;
}
Array Stabilization (GCD version)
- 读题可以得到当前这个位置被修改k次后的值是 \(gcd(a_i,....,a_{k+i})\)
- 所以可以用ST表维护区间 \(GCD\) ,发现 \(k\) 可以枚举,而且有单调性,考虑二分
#include<bits/stdc++.h>
using namespace std;
int t,n;
int lg[400010];
int st[400010][30];
int a[400010];
int gcd(int x,int y){
if(y==0) return x;
return gcd(y,x%y);
}
int m;
bool check(int x){
int ans=0;
for(int i=1;i<=m-x;i++){
if(!ans) ans=gcd(st[i][lg[x+1]],st[i+x-(1<<lg[x+1])+1][lg[x+1]]);
else if(ans!=gcd(st[i][lg[x+1]],st[i+x-(1<<lg[x+1])+1][lg[x+1]])) return 0;
}
return 1;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL),cout.tie(NULL);
lg[0]=-1;
for(int i=1;i<=400000;i++){
lg[i]=lg[i>>1]+1;
}
cin>>t;
while(t--){
cin>>n;
lg[0]=0;
for(int i=1;i<=n;i++){
cin>>a[i]; a[i+n]=a[i];
st[i][0]=a[i];
st[i+n][0]=a[i];
}
m=n*2;
for(int j=1;j<=lg[m];j++){
for(int i=1;i<=m-(1<<j)+1;i++){
st[i][j]=gcd(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
}
int l=0,r=n-1;
int ans=n-1;
while(l<=r){
int mid=l+r>>1;
if(check(mid)) r=mid-1,ans=mid;
else l=mid+1;
}
cout<<ans<<'\n';
}
return 0;
}
并查集
- 顾名思义,把两个集合合并,用来查询归属关系
- 用来查询敌对等等
怎么实现?
- 我们可以不断寻找一个点的父亲来,找到真正的最上面的祖先
- 合并即把一个点的祖先的父亲设为另一个的祖先即可
int find(int x){
if(x==fa[x]) return x;
return find(fa[x]);
}
void merge(int x,int y){
int f1=find(x),f2=find(y);
fa[f1]=f2;
}
优化一:压缩路径
- 可以把类似与把链变成树的方式来压缩路径
- 例如:把假设有一条链,把最下面的节点的父亲直接设为祖先,这样复杂度就大大降低
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
优化二:按秩合并
- 我们知道合并时把小的往大的合并,一定比大的往小的合并更优,所以可以记录大小
void merge(int x,int y){
int f1=find(x),f2=find(y);
if(f1==f2) return ;
if(siz[f1]>siz[f2]) swap(s1,s2);
siz[s2]+=siz[f1];
}
亲戚
- 板子套代码即可
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a,b,d[30000],c,h,p;
int find(int x){
if(d[x]!=x){
d[x]=find(d[x]);
}
return d[x];
}
int bing(int x,int y){
int hx=find(x);
int hy=find(y);
if(hx!=hy){
d[hx]=hy;
}
}
int main(){
cin>>n>>m>>p;
for(int i=1;i<=n;i++){
d[i]=i;
}
for(int i=1;i<=m;i++){
cin>>a>>b;
bing(a,b);
}
for(int i=1;i<=p;i++){
cin>>c>>h;
if(find(c)==find(h)){
cout<<"Yes"<<endl;
}
else{
cout<<"No"<<endl;
}
}
return 0;
}
2024 [NOI2001] 食物链
- 看这道题可以发现吃与被吃的关系只有三种,所以可以维护种类并查集。我吃它,那它吃的吃我
- 给每一个维护一个并查集,通过吃与被吃的关系将他们用并查集维护一下
- 判掉题目的不满足情况,
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int n,k,fa[N*3],op,x,y;
int find(int x){
if(x==fa[x]){
return x;
}
return fa[x]=find(fa[x]);
}
void merge(int x,int y,int k){
if(k==1){
fa[find(y)]=find(x);
fa[find(y+n)]=find(x+n);
fa[find(y+2*n)]=find(x+2*n);
}
else{
fa[find(y+n)]=find(x+2*n);
fa[find(y+2*n)]=find(x);
fa[find(y)]=find(x+n);
}
}
int main(){
cin>>n>>k;
int ans=0;
for(int i=1;i<=3*n;i++){
fa[i]=i;
}
for(int i=1;i<=k;i++){
cin>>op>>x>>y;
if((x>n)||(y>n)){
ans++;
continue;
}
if(op==2&&x==y){
ans++;
continue;
}
if(op==1){
if(find(x+n)==find(y)||find(x)==find(y+n)){
ans++;
continue;
}
}
else{
if(find(x)==find(y)||find(x)==find(y+n)){
ans++;
continue;
}
}
merge(x,y,op);
}
cout<<ans;
return 0;
}
树状数组
- 支持区间修改,单点查询。单点修改,区间查询的数据结构
- 修改与查询都是 \(\operatorname{O(\log n)}\)
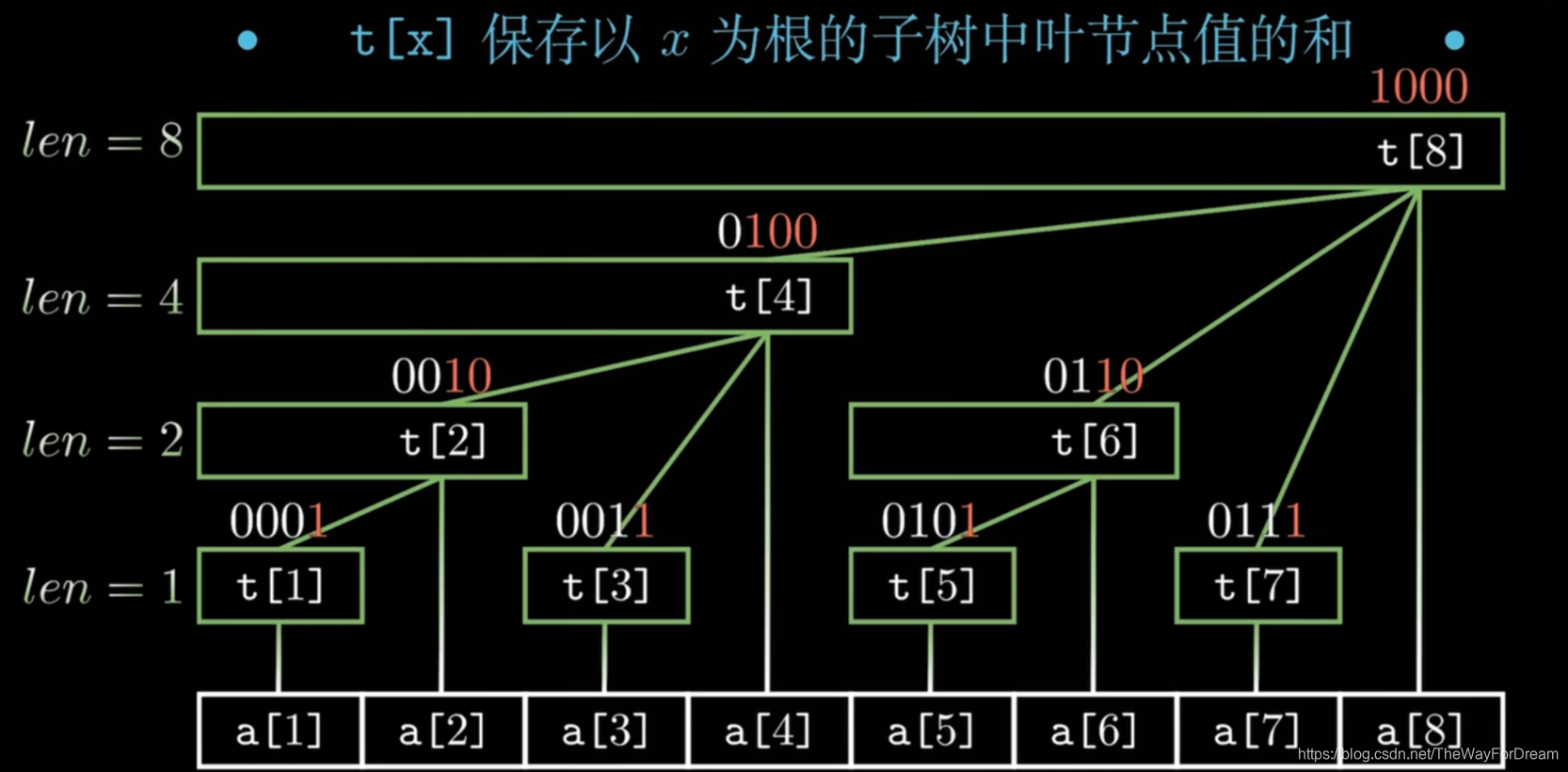
这是一棵基本的树状数组;
在学习前先介绍一个 $lowbit(x) $ 这个函数可以求出某个数二进制数的最后一个1所带的0的十进制大小
int lowbit(int x){
return x&-x;
}
- 接下来开始正题
- 接下来第一个单点修改,区间查询。
\(a_k\) 的意义是什么?
即是 \({k-lowbit(k)+1} {\ — \ } {\ }k\) 的这个区间的值
看上图得知当我们修改了 \(a_1\) 的值时,\(t_1,t_2,t_4,t_8\) 的权值都需要修改
在修改了 \(a_3\) 的值时,\(t_3,t_4,t_8\) 的权值修改。
综上,我们发现了 当修改了 \(a_k\) 的值时, \(a_{k+lowbit(k)}\),\({k+lowbit(k)+lowbit(k+lowbit(k)))}...\) 的值都会修改,复杂度为 \(\operatorname{O(\log n)}\)
void merge(int x,int k){
for(int i=x;i<=n;i+=lowbit(i)){
tree[x]+=k;
}
}
修改写完了,接下来改写查询了。
举个例子,假如我们要求前7个的和,那查询的数组应该是 \(tree[7],tree[6],tree[4]\) 的总和
假如要求前4个的和,那查询的数组应该是 \(tree[4]\)
综上,我们发现了 查询前 \(k\) 个值时,应该要查询 \(tree_{k},tree_{k-lowbit(k)},tree_{k-lowbit(k)-lowbit(k-lowbit(k))}\) 的权值
int query(int x){
int sum=0;
while(x){
sum+=tree[x];
x-=lowbit(x);
}
return sum;
}
要求区间和的话,用类似前缀和的方法即可
- 区间修改,单点查询
接下来开始修改操作
维护一个差分数组,因为差分数组的特性,所以只要将 \(1\) ~ \(r\) 的差分数组用树状数组存储一下即可
修改则为
- merge(r,k),merge(l-1,-k)
查询是什么?
- 因为差分数组的特性,当前这个位置的值是前k个差分数组的和,因为我们是树状数组,所以2可以类似上面区间查询的方法
- 用\(\operatorname{O(\log n)}\)的时间查询
例题
逆序对
- 这是一个经典的树状数组的题目,也可以用归并解决
- 观察到n一定, \(a_i\) 的大小超出数组范围,考虑先进行离散化
接着我们得到了离散化后的数组,可以考虑在当前位置之前比自己小的个数有多少,比自己大的数量就是,前面有多少个数减去小于等于当前数的数量,统计之后再在当前大小加一
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,a[500010],cnt,tree[500010],t[500010];
void lsh(){
int tot=unique(1+t,1+t+cnt)-t-1;
for(int i=1;i<=n;i++){
a[i]=lower_bound(1+t,1+t+tot,a[i])-t;
}
}
int lowbit(int x){
return x&-x;
}
int sum(int x){
int ans=0;
while(x){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
void add(int x,int k){
for(int i=x;i<=n;i+=lowbit(i)){
tree[i]+=k;
}
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
t[++cnt]=a[i];
}
sort(t+1,t+1+cnt);
lsh();
int num=0;
for(int i=1;i<=n;i++){
num+=i-1-sum(a[i]);
add(a[i],1);
}
cout<<num;
return 0;
}
楼兰图腾
- 观察题目,发现这里可以将每一个点作为顶点来做具体分析,维护左边多少比我大的,右边多少比我大的,然后减一下,得到左边和右边多少比我小的。
- 最后统计,将答案累加
#include<bits/stdc++.h>
using namespace std;
long long n,y[10000100],ans,sum,xx[10000010],yy[10000010],xx1[1000100],yy1[10000010];
int tree1[2000010],tree2[2000010];
int lowbit(int x){
return x&-x;
}
void add1(int x,int k){
while(x<=n){
tree1[x]+=k;
x+=lowbit(x);
}
}
int sum1(int x){
int num=0;
while(x){
num+=tree1[x];
x-=lowbit(x);
}
return num;
}
void add2(int x,int k){
while(x<=n){
tree2[x]+=k;
x+=lowbit(x);
}
}
int sum2(int x){
int num=0;
while(x){
num+=tree2[x];
x-=lowbit(x);
}
return num;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>y[i];
}
for(int i=1;i<=n;i++){
xx[i]=sum1(y[i]-1);
xx1[i]=sum1(n)-sum1(y[i]);
add1(y[i],1);
}
for(int i=n;i>=1;i--){
yy[i]=sum2(y[i]-1);
yy1[i]=sum2(n)-sum2(y[i]);
add2(y[i],1);
}
long long ans=0,sum=0;
for(int i=1;i<=n;i++){
ans+=xx[i]*yy[i];
sum+=xx1[i]*yy1[i];
}
cout<<sum<<" "<<ans;
return 0;
}
校门外的树
- 读题感觉可以贪心,但其实是错的,因为无法实时维护
- 正解是树状数组,维护两个树状数组,一个维护右括号,一个维护左括号。
- 发现查询时答案应该是区间内有多少种,也是右区间前左括号数量减去左区间前右括号数量
#include<bits/stdc++.h>
using namespace std;
int n,m;
int l,r;
int tree1[50010],tree2[50010];
int lowbit(int x){
return x&-x;
}
void merge1(int x){
while(x<=n){
tree1[x]++;
x+=lowbit(x);
}
}
void merge2(int x){
while(x<=n){
tree2[x]++;
x+=lowbit(x);
}
}
int query1(int x){
int num=0;
while(x){
num+=tree1[x];
x-=lowbit(x);
}
return num;
}
int query2(int x){
int num=0;
while(x){
num+=tree2[x];
x-=lowbit(x);
}
return num;
}
signed main(){
cin>>n>>m;
while(m--){
int op,l,r;
cin>>op>>l>>r;
if(op==1){
merge1(l),merge2(r);
}
else{
cout<<query1(r)-query2(l-1);
}
}
return 0;
}
线段树
思想:将数据存入一颗线段树中,通过查询然后优点是因为树的高度是\((\log n)\) ,所以查询与修改的时间均为 \(\operatorname{O(\log n)}\) 。
具体怎么实现?
\(pushup\)
- 先介绍一个函数 \(pushup\) ,有什么用呢?具体是合并两个区间的,实现即为左区间和右区间的信息结合
tree[i].add=tree[i<<1].add+tree[i<<1|1].add
tree[i].maxn=max(tree[i<<1].maxn,tree[i<<1|1].maxn);
...
建树
- 建树,将一个区间分成两个小区间,再通过递归的方式来把每一个区间分成两个,并附上儿子节点,直到长度为一,即左端点等于右端点,当满足时,就把他这一个点来附上一个值,最后合并区间即可
void build(int p,int l,int r){
if(l==r){
tree[p].add=a[l];
tree[p].maxn=a[l];
return ;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
push_up(p);
}
单点修改
- 怎么实现呢?每次二分一个点,可以通过每次要是值小了就缩小 \(r\),否则就放大 \(l\),如果最后缩出来可以匹配了就直接更新值,再用 \(push_up\) 操作更新大区间
void merge(int k,int p,int l,int r,int x){
if(l==r){
tree[p].add+=k;
return ;
}
int mid=(l+r)>>1;
if(x<=mid){
merge(k,p<<1,l,mid,x,y);
}
if(mid+1<=x){
merge(k,p<<1|1,mid+1,r,x,y);
}
push_up(p);
}
区间修改
- 这下就变得难一些了,我们该怎么办呢?接下来又要介绍一个函数
\(pushdown\)
- 这个函数是用来在区间操作中在不断缩小范围的同时顺便给儿子节点附上值的操作
- 具体实现是这样,就是因为这个区间掌管 \(l\) ~ \(r\) ,所以左儿子掌管 \(l~mid\) ,右儿子掌管 \(mid+1\) ~ \(r\) ,那么这个区间加上,每一个加上 \(k\) ,掌管这个区间的 \(tree_p\) 要加上 \((r-l+1)*k\),左儿子要加上 \((mid-l)*k\) ,右儿子加上 \((r-mid+1)*k\) ,接着一直下传,下传的值用懒标记维护,要累加起来,为什么呢?因为当我们不需要用到这个值的时候可以先不把儿子更新,因为父亲节点的懒标记已经存好了可以让儿子下一次操作使用,所以如果不累加的话值就会少加到一些。
void push_down(int p,int l,int r){
if(tree[p].tag>0){
int mid=(l+r)>>1;
tree[ls].tag+=tree[p].tag;
tree[rs].tag+=tree[p].tag;
tree[ls].add+=(mid-l+1)*tree[p].tag;
tree[rs].add+=(r-mid)*tree[p].tag;
tree[p].tag=0;
}
}
- 最后类似单点修改的其他操作
void merge(int k,int p,int l,int r,int x,int y){
if(x>r||y<l)
return ;
if(x<=l&&y>=r){
tree[p].tag+=k;
tree[p].add+=k*(r-l+1);
return ;
}
push_down(p,l,r);
int mid=(l+r)>>1;
if(x<=mid){
merge(k,ls,l,mid,x,y);
}
if(mid+1<=y){
merge(k,rs,mid+1,r,x,y);
}
push_up(p);
}
区间查询
- 在范围内就返回当前范围掌管的值
- 否则就去找值
- 当然要使要用到某个区间的值还需要及时下传懒标记
int query(int p,int l,int r,int x,int y){
if(x<=l&&y>=r){
return tree[p].add;
}
push_down(p,l,r);
int ans=0;
int mid=(l+r)>>1;
if(x<=mid){
ans+=query(ls,l,mid,x,y);
}
if(mid+1<=y){
ans+=query(rs,mid+1,r,x,y);
}
return ans;
}
例题:
4145 上帝造题的七分钟 2 / 花神游历各国
- 读题发现这是一道模版题,直接维护区间开平方,像模板一样维护区间和,但是要注意 \(\sqrt{1}\) 为一,可以直接跳过,修改值会出问题
#include<bits/stdc++.h>
using namespace std;
struct node{
long long pre,maxn;
}t[400010];
long long n,a[100010],m,k,l,r;
void build(int p,int l,int r){
if(l==r){
t[p].maxn=t[p].pre=a[l];
return ;
}
int mid=(l+r)>>1;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
t[p].pre=t[p*2].pre+t[p*2+1].pre;
t[p].maxn=max(t[p*2].maxn,t[p*2+1].maxn);
}
void change(int p,int x,int y,int l,int r){
if(x<=l&&y>=r&&l==r){
t[p].maxn=t[p].pre=sqrt(t[p].pre);
return;
}
int mid=(l+r)>>1;
if(x<=mid&&t[p*2].maxn>1){
change(p*2,x,y,l,mid);
}
if(y>mid&&t[p*2+1].maxn>1){
change(p*2+1,x,y,mid+1,r);
}
t[p].pre=t[p*2].pre+t[p*2+1].pre;
t[p].maxn=max(t[p*2].maxn,t[p*2+1].maxn);
}
long long find(int p,int x,int y,int l,int r){
if(x<=l&&y>=r)
return t[p].pre;
int mid=(l+r)>>1;
long long ans=0;
if(x<=mid){
ans+=find(p*2,x,y,l,mid);
}
if(y>mid){
ans+=find(p*2+1,x,y,mid+1,r);
}
return ans;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
build(1,1,n);
cin>>m;
while(m--){
cin>>k>>l>>r;
if(l>r)
swap(l,r);
if(k==0){
change(1,l,r,1,n);
}
else{
cout<<find(1,l,r,1,n)<<endl;
}
}
return 0;
}
P4513 小白逛公园
- 读题发现这道题要维护最大子段和
- 我们知道一个最大子段和要么是一个区间的最大前缀和,要么是一个区间的最大后缀和,要么是一个区间的最大后缀和最大前缀和
- 所以我们可以用线段树动态维护这些值
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e5+10;
int n,m,op;
int x,y;
int a[MAXN];
int ls(int p){
return p<<1;
}
int rs(int p){
return p<<1|1;
}
struct node{
int add,maxn,maxnl,maxnr;
}t[MAXN<<2];
void pushup(int x){
t[x].add=t[ls(x)].add+t[rs(x)].add;
t[x].maxnl=max(t[ls(x)].maxnl,t[ls(x)].add+t[rs(x)].maxnl);
t[x].maxnr=max(t[rs(x)].maxnr,t[rs(x)].add+t[ls(x)].maxnr);
t[x].maxn=max(max(t[ls(x)].maxn,t[rs(x)].maxn),t[ls(x)].maxnr+t[rs(x)].maxnl);
}
void build(int p,int l,int r){
if(l==r){
t[p].add=t[p].maxn=t[p].maxnl=t[p].maxnr=a[l];
return ;
}
int mid=l+r>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
pushup(p);
}
void merge(int p,int l,int r,int x,int w){
if(l==r){
t[p].add=t[p].maxn=t[p].maxnl=t[p].maxnr=w;return ;
}
int mid=l+r>>1;
if(mid>=x){
merge(ls(p),l,mid,x,w);
}
else{
merge(rs(p),mid+1,r,x,w);
}
pushup(p);
}
node query(int p,int l,int r,int x,int y){
node tmp;
if(l>=x&&r<=y){
return t[p];
}
int mid=l+r>>1;
if(x>mid){
return query(rs(p),mid+1,r,x,y);
}
else if(y<=mid){
return query(ls(p),l,mid,x,y);
}
else{
node A=query(ls(p),l,mid,x,y),b=query(rs(p),mid+1,r,x,y);
tmp.add=A.add+b.add;
tmp.maxnl=max(A.maxnl,A.add+b.maxnl);
tmp.maxnr=max(b.maxnr,b.add+A.maxnr);
tmp.maxn=max(max(A.maxn,b.maxn),A.maxnr+b.maxnl);
return tmp;
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
build(1,1,n);
while(m--){
cin>>op;
if(op==1){
cin>>x>>y;
if(x>y) swap(x,y);
cout<<query(1,1,n,x,y).maxn<<'\n';
}
else{
cin>>x>>y;
merge(1,1,n,x,y);
}
}
return 0;
}
[COCI2010-2011#6] STEP
- 读题可以发现这道题要求最长相邻不同的长度
- 主要问题在合并,可以维护前缀最大,后缀最大,然后判断中间两个数是否相异,即是否可以合并
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000010],op,l,r,d,p,k,mod;
struct tree{
long long l,r;
long long pre,mul,add,len1,len2,len;
}t[4000100];
void ansit(int p,int l,int r){
long long mid=(l+r)>>1;
long long ll=mid-l+1,rr=r-mid;
t[p].len1=t[p*2].len1,t[p].len2=t[p*2+1].len2,t[p].len=max(t[p*2].len,t[p*2+1].len);
if(a[mid]!=a[mid+1]){
t[p].len=max(t[p].len,t[p*2+1].len1+t[p*2].len2);
if(t[p*2].len==ll)
t[p].len1=ll+t[p*2+1].len1;
if(t[p*2+1].len==rr){
t[p].len2=rr+t[p*2].len2;
}
}
}
void build(int p,int l,int r){
t[p].len=1,t[p].len1=1,t[p].len2=1;
if(l==r){
return;
}
long long mid=(l+r)>>1;
build(2*p,l,mid);
build(2*p+1,mid+1,r);
ansit(p,l,r);
}
void add(int p,int l,int r,int z){
if(l==r&&l==z){
a[l]^=1;
return;
}
int mid=(l+r)>>1;
if(z<=mid){
add(p*2,l,mid,z);
}
else{
add(p*2+1,mid+1,r,z);
}
ansit(p,l,r);
}
int main(){
cin>>n>>m;
build(1,1,n);
for(int i=1;i<=m;i++){
cin>>op;
add(1,1,n,op);
cout<<t[1].len<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号