强联通分量及缩点
一、dfs森林和强联通分量
1.dfs森林
dfs森林就是dfs后形成的树形结构。
四种边(有向图生成的dfs森林):
1.树边:在dfs森林中的边。
2.返祖边:从一个节点指向其祖先的边。
3.前向边:从一个点指向其子孙节点的边。
4.横叉边:从一个点指向一个与其没有血缘关系的节点(横叉边一定是由一个点指向一个之前已经访问过的点)。
图\(G\):
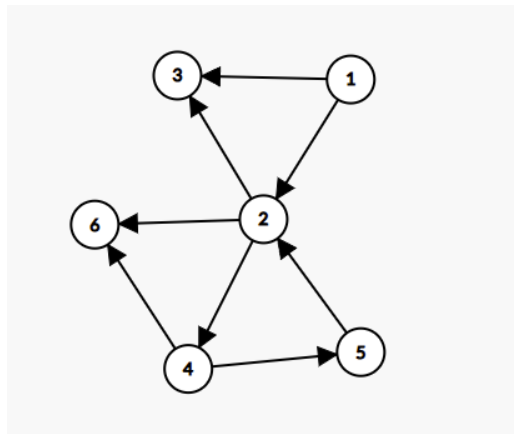
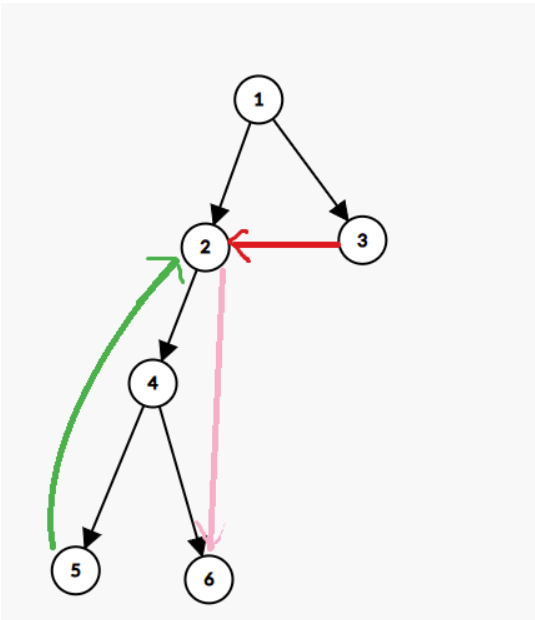
图\(G\)的dfs生成树:
黑边为树边,绿边为返祖边,粉边为前向边,红边为横叉边。
2.强联通分量(scc)
弱连通:有向图中将无向边后任意两点可达。
强联通:有向图中任意两个点都互相可达。
强联通分量:有向图中极大强联通的子图。
强联通具有传递性:若\(u\)与\(v\)强联通,\(u\)与\(w\)强联通,则\(v\)与\(w\)强联通。
二、强联通分量的\(Tarjan\)和\(Kosaraju\)算法
1.\(Tarjan\)算法
可以注意到一个强联通分量在dfs森林中一定是连续的一块。
也可以认为是以一个点为根的子树。
对于每个节点记录以下两个信息:
1.\(dfn[i]:\)\(i\)号点的dfs序。
2.\(low[i]:\)\(i\)号点能到达的最小的在栈中的节点的dfs序。
dfs时维护一个栈,记录所有为成为scc的点。
可以发现:一个强联通分量中只有一个点的\(dfn[i]=low[i]\),也就是该强联通分量的根节点。
对于节点\(u\),枚举出边\((u,v)\)。
1.若\(dfn[v]=0\),即为访问过\(v\)节点,继续dfs\(v\)节点,并更新\(low[u]=min(low[u],low[v])\)(\(v\)能到达的节点,\(u\)也能到达).
2.若\(dfn[v]\neq 0\)且节点\(v\)还在栈中,说明\(v\)目前不属于其他强联通分量,更新\(low[u]=min(low[u],dfn[v])\).
3.若\(dfn[v]\neq 0\)且节点\(v\)不在栈中,说明\(v\)已经属于其他的强联通分量,则不更新。
若一个节点的\(dfn[i]=low[i]\),则从该节点至栈末为一个强联通分量。
code
inline void dfs(int x){
dfn[x]=low[x]=++cnt;
stk[++top]=x;
ins[x]=1;
for(auto to : E[x]){
if(!dfn[to]){
dfs(to);
low[x]=min(low[x],low[to]);
}
else if(ins[to]) low[x]=min(low[x],dfn[to]);
}
if(dfn[x]==low[x]){
now.clear();
while(top){
int v=stk[top]; --top;
ins[v]=0;
now.push_back(v);
if(v==x) break;
}
sort(now.begin(),now.end());
scc.push_back(now);
}
return ;
}
2.\(Kosaraju\)算法
关键性质:dfs的出栈序列为返图的拓扑序(即拓扑序的反序)。
推论:dfs的出栈序列的最后一个点一定是一个源点。
\(Kosaraju\)算法会进行两次dfs。
第一次dfs记录出栈序列;
第二次dfs在出栈序列上倒序在反图上dfs,一个点可以到达的点和它在同一个强联通分量中。
正确性说明(并非严谨证明)
第一次dfs后形成的出栈序列为拓扑序的反序,则说明出栈序列中后面的点可以到达前面的点;
第二次dfs在反图上进行,则在反图中后面的点可以到达前面的点说明在原图中前面的点可以到达后面的点。
则前面的点与后面的点强联通,所以该算法正确。
code
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define inf 1e10
#define eps 1e-9
#define endl "\n"
#define il inline
#define ls 2*k
#define rs 2*k+1
using namespace std;
const int N=3e5+5,M=1e7+5;
const int mod=998244353;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
return x*f;
}
bool vis[N];
int n,m,stk[N],top;
vector<int>E[N],e[N];
vector<int>now;
vector< vector<int> >scc;
inline void dfs(int x){
vis[x]=1;
for(auto to : E[x]){
if(vis[to]) continue;
dfs(to);
}
stk[++top]=x;
return ;
}
inline void dfs2(int x){
vis[x]=1;
for(auto to : e[x]){
if(vis[to]) continue;
dfs2(to);
}
now.push_back(x);
return ;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m;
for(int i=1,u,v;i<=m;i++){
cin>>u>>v;
E[u].push_back(v);
e[v].push_back(u);
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs(i);
memset(vis,0,sizeof(vis));
for(int i=top;i>=1;i--){
if(vis[stk[i]]) continue;
dfs2(stk[i]);
sort(now.begin(),now.end());
scc.push_back(now);
now.clear();
}
sort(scc.begin(),scc.end());
for(auto now : scc){
for(auto cur : now)
cout<<cur<<' ';
cout<<'\n';
}
return 0;
}
三、缩点和DP
可以发现将原图中的强联通分量缩成一个点后,原图就变成了一个DAG(有向无环图)。
然后就可以在这个DAG上按拓扑序dp。
关于新图的拓扑序
不必再拓扑排序一遍。
由$ Kosaraju $算法的重要结论可以推出:
在\(Tarjan\)实现过程中,scc的编号顺序其实就相当于出栈序列。
所以\(Tarjan\)中scc的编号顺序为新图拓扑序的逆序(反图拓扑序)。
四、题集
缩点+dp,原问题等价于求新图最长路(点有点权)+ 计数。
code
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define inf 1e10
#define eps 1e-9
#define endl "\n"
#define il inline
#define ls 2*k
#define rs 2*k+1
using namespace std;
const int N=1e6+5,M=1e7+5;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
return x*f;
}
bool ins[N];
int n,m,mod,cnt,top,len,tim,f[N],way[N],vis[N];
int dfn[N],low[N],stk[N],bel[N],siz[N],outd[N];
vector<int>E[N],scc[N];
inline void dfs(int x){
dfn[x]=low[x]=++len;
stk[++top]=x,ins[x]=1;
for(auto to : E[x]){
if(!dfn[to]){
dfs(to);
low[x]=min(low[x],low[to]);
}
else if(ins[to]) low[x]=min(low[x],dfn[to]);
}
if(dfn[x]==low[x]){
cnt++;
while(1){
int v=stk[top]; --top;
ins[v]=false;
siz[cnt]++;
bel[v]=cnt;
scc[cnt].push_back(v);
if(v==x) break;
}
f[cnt]=siz[cnt],way[cnt]=1;
}
return ;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m>>mod;
for(int i=1,u,v;i<=m;i++){
cin>>u>>v;
E[u].push_back(v);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) dfs(i);
int Max=0,ans=0;
for(int i=cnt;i>=1;i--){
++tim;
for(auto u : scc[i]){
for(auto v : E[u]){
if(bel[u]==bel[v] || vis[bel[v]]==tim) continue;
vis[bel[v]]=tim;
if(f[bel[v]]<f[i]+siz[bel[v]]) f[bel[v]]=f[i]+siz[bel[v]],way[bel[v]]=way[i];
else if(f[bel[v]]==f[i]+siz[bel[v]]) way[bel[v]]=(way[bel[v]]+way[i])%mod;
}
}
if(f[i]>Max) Max=f[i],ans=way[i];
else if(f[i]==Max) ans=(ans+way[i])%mod;
}
cout<<Max<<'\n'<<ans<<'\n';
return 0;
}
/*
强联通分量编号的顺序是出栈顺序
也就是拓扑序的逆序
*/
缩点+dp.
code
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define inf 1e10
#define eps 1e-9
#define endl "\n"
#define il inline
#define ls 2*k
#define rs 2*k+1
using namespace std;
const int N=5e5+5,M=1e7+5;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
return x*f;
}
bool isbar[N],ins[N],ext[N];
int n,m,s,p,len,cnt,a[N],f[N],tim,bel[N];
int stk[N],top,dfn[N],low[N],siz[N],vis[N];
vector<int>E[N],scc[N];
inline void dfs(int x){
dfn[x]=low[x]=++len;
stk[++top]=x,ins[x]=1;
for(auto to : E[x]){
if(!dfn[to]){
dfs(to);
low[x]=min(low[x],low[to]);
}
else if(ins[to]) low[x]=min(low[x],dfn[to]);
}
if(low[x]==dfn[x]){
cnt++;
bool flag=0;
while(top){
int v=stk[top--];
ins[v]=false;
siz[cnt]+=a[v],bel[v]=cnt;
scc[cnt].push_back(v);
if(isbar[v]) ext[cnt]=1;
if(v==s) flag=1;
if(v==x) break;
}
if(flag) f[cnt]=siz[cnt];
}
return ;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>m;
for(int i=1,u,v;i<=m;i++){
cin>>u>>v;
E[u].push_back(v);
}
for(int i=1;i<=n;i++) cin>>a[i],f[i]=-inf;
cin>>s>>p;
for(int i=1,x;i<=p;i++)
cin>>x,isbar[x]=1;
for(int i=1;i<=n;i++)
if(!dfn[i]) dfs(i);
for(int i=cnt;i>=1;i--){
++tim;
for(auto u : scc[i])
for(auto v : E[u]){
int to=bel[v];
if(to==i || vis[to]==tim) continue;
if(f[to]<f[i]+siz[to]) f[to]=f[i]+siz[to];
vis[to]=tim;
}
}
int ans=0;
for(int i=1;i<=cnt;i++)
if(ext[i]) ans=max(ans,f[i]);
cout<<ans<<'\n';
return 0;
}
缩点+dp,注意要优化建图方式。
可以对于每一行和每一列建一个虚拟节点,同时注意这个虚拟节点只需要连接这一行或这一列中实际存在的节点(有宝藏的节点)。
这样就将边数从\(n^2\)级别优化为\(n\)级别。
code
#include <bits/stdc++.h>
#define int long long
#define ull unsigned long long
#define inf 1e10
#define eps 1e-9
#define endl "\n"
#define il inline
#define ls 2*k
#define rs 2*k+1
using namespace std;
const int N=1e6+5,M=1e7+5;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
return x*f;
}
bool ins[N];
int n,r,c,len,cnt,f[N],tim,bel[N];
int stk[N],top,dfn[N],low[N],siz[N],vis[N],qwq;
vector<int>E[N],scc[N],R[N],C[N];
map<int,int>mp1,mp2;
map< pair<int,int>,int >mp;
map<int,bool>exist;
struct point{ int x,y,op; }p[N];
inline void dfs(int x){
dfn[x]=low[x]=++len;
stk[++top]=x,ins[x]=1;
for(auto to : E[x]){
if(!dfn[to]){
dfs(to);
low[x]=min(low[x],low[to]);
}
else if(ins[to]) low[x]=min(low[x],dfn[to]);
}
if(low[x]==dfn[x]){
cnt++;
while(top){
int v=stk[top--];
ins[v]=false;
bel[v]=cnt;
if(exist[v]) siz[cnt]++;
scc[cnt].push_back(v);
if(v==x) break;
}
f[cnt]=siz[cnt];
}
return ;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin>>n>>r>>c;
for(int i=1,x,y,op;i<=n;i++){
cin>>x>>y>>op;
if(!mp[{x,y}]) mp[{x,y}]=++qwq;
p[i]={x,y,op};
exist[mp[{x,y}]]=1;
R[x].push_back(i);
C[y].push_back(i);
}
for(int i=1;i<=n;i++){
if(p[i].op==1){
if(!mp1[p[i].x]) mp1[p[i].x]=++qwq;
E[mp[{p[i].x,p[i].y}]].push_back(mp1[p[i].x]);
}
else if(p[i].op==2){
if(!mp2[p[i].y]) mp2[p[i].y]=++qwq;
E[mp[{p[i].x,p[i].y}]].push_back(mp2[p[i].y]);
}
else{
for(int dx=-1;dx<=1;dx++)
for(int dy=-1;dy<=1;dy++){
int nowx=p[i].x+dx,nowy=p[i].y+dy;
if(!nowx || !nowy || nowx>r || nowy>c || (nowx==p[i].x && nowy==p[i].y)) continue;
if(!mp[{nowx,nowy}]) continue;
E[mp[{p[i].x,p[i].y}]].push_back(mp[{nowx,nowy}]);
}
}
}
for(int i=1;i<=r;i++){
if(R[i].empty()) continue;
for(auto u : R[i]) E[mp1[i]].push_back(u);
}
for(int i=1;i<=c;i++){
if(C[i].empty()) continue;
for(auto u : C[i]) E[mp2[i]].push_back(u);
}
for(int i=1;i<=qwq;i++)
if(!dfn[i]) dfs(i);
for(int i=cnt;i>=1;i--){
++tim;
for(auto u : scc[i])
for(auto v : E[u]){
int to=bel[v];
if(to==i || vis[to]==tim) continue;
if(f[to]<f[i]+siz[to]) f[to]=f[i]+siz[to];
vis[to]=tim;
}
}
int ans=0;
for(int i=1;i<=cnt;i++) ans=max(ans,f[i]);
cout<<ans<<'\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号