2023.8pyyz集训模拟赛总结
气崩了气崩了,本来还用zybuluo.com,结果他访问不了了,算了,回到我的Typora和cnblogs了。
不是,我的Typora,图床怎么你了。
待填坑题目
D2 T5 玩树
D4 T4 运输货物 T5 道路规划
D5 T5 咕咕咕
D6 T4 Dove的疑惑 T5 K直径生成树
D7 T4 迷宫
模拟赛1
T1 三值的排序
在这个任务中可能的值只有三种1,2和3 。 我们用交换的方法把他排成升序的。
写一个程序计算出,给定的一个 1,2,3 组成的数字序列,排成升序所需的最小交换 次数。
\(1 \le N \le 1000\)
贪心一波,猜一波结论,没了
T2 日记
T组数据 给定n,k ,询问不超过n的数中能够表示成连续的k个质数之和的最大的数是多少?
\(1 \le T < 2000\) , \(1 \le N \le 10^6\) , \(k\) 为整数,且 \(\le 10^9\) 。
预处理质数的前缀和,没了。
T3 分蛋糕
今天 小Y考蛋糕吃,小Z闻到蛋糕的香气于是跑过来想分着吃。
蛋糕是圆形的,从蛋糕中某点开始将蛋糕放射状切为N块,按逆时针顺序编号为1到 N。切了之后的第i块蛋糕的大小为a_i 。由于切蛋糕的人刀功很不好,所以a_i互不相同。
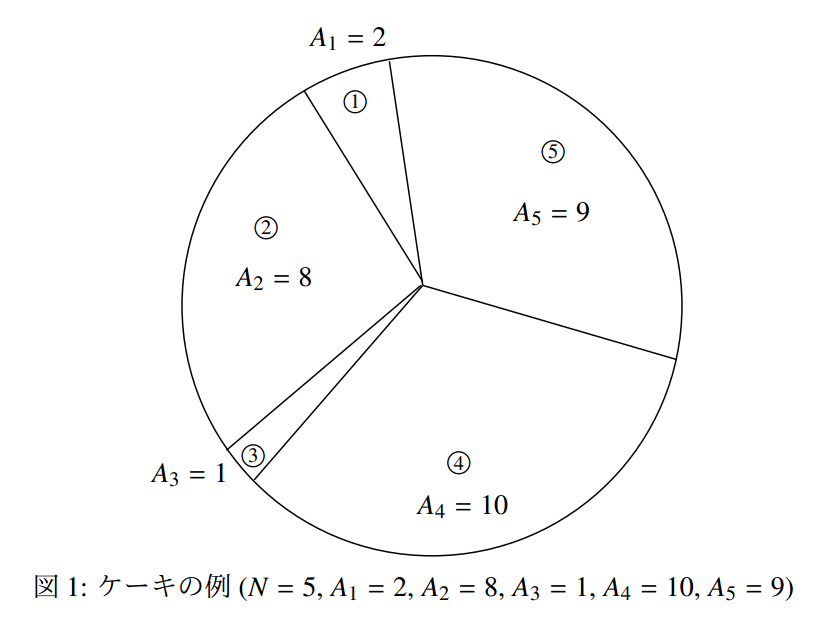
小Y和 小Z按照以下方法分这n块蛋糕:
-
首先 小Y 从这 块蛋糕中任选一块取走;
-
然后,从小Z开始,小Z和 小Y交替地从剩下的蛋糕中选出一块取走。不过, 当且仅当一块蛋糕两旁的蛋糕至少有一块已经被选择,这块蛋糕才能被选择。如 果可供选择的蛋糕有多个,小Z会选择最大的一个,而 小Y可以任选一个。
小Y想让自己所得到的蛋糕大小的合计值最大。
\(1 \le N \le 2000,1 \le A_i \le 10^9\) ,每个 \(A_i\) 都不同。
考虑拆环,然后进行区间dp,没了。
T4 都市
有N 个数,但不给你,而是给了你 \(N\times (N-1)/2\)个数,代表它们两两的和。
那么,这N个数是多少呢?
\(1 \le N \le 300\) , \(N\) 个数均不超过 \(10^8\) 。
将读入的数字排序, \(a_1+a_2\) 和 \(a_1+a_3\) 必为最小值与次小值,考虑枚举 \(a_1+a_3\) 是哪一个数字,解出 \(a_1,a_2,a_3\) 。
将 \(a_1+a_2,a_1+a_3,a_2+a_3\) 删掉,此时集合内最小值必为 \(a_1+a_4\) ,解出 \(a_4\) ,删掉 \(a_1+a_4,a_2+a_4,a_3+a_4\) 以此类推,解出集合。
使用multiset维护。
#include<bits/stdc++.h>
#include<cstdio>
#define lowbit(x) ((x)&(-x))
#define fir first
#define se second
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=310,M=9e4+100;
int sum[M],a[N];
int ans[M][N],cnt;
int n,m;
stack<int>st;
multiset<int>s;
void work(){
while(!st.empty()){
s.insert(st.top());
st.pop();
}
for(int i=1;i<=3;i++)
for(int j=i+1;j<=3;j++){
s.erase(s.find(a[i]+a[j]));
st.push(a[i]+a[j]);
}
for(int i=4;i<=n;i++){
int t=*s.begin();
a[i]=t-a[1];
if(a[i]<a[i-1])return;
for(int j=1;j<i;j++){
if(s.find(a[i]+a[j])==s.end())return;
s.erase(s.find(a[i]+a[j]));
st.push(a[i]+a[j]);
}
}
++cnt;
for(int i=1;i<=n;i++)ans[cnt][i]=a[i];
}
int main(){
scanf("%d",&n);
m=n*(n-1)/2;
for(int i=1;i<=m;i++)scanf("%d",&sum[i]);
sort(sum+1,sum+m+1);
for(int i=1;i<=m;i++)s.insert(sum[i]);
for(int i=3;i<=n;i++){
int t=sum[1]+sum[2]+sum[i];
if(i>3&&sum[i]==sum[i-1])continue;
if(t&1)continue;
t/=2;
a[1]=t-sum[i];a[2]=t-sum[2];a[3]=t-sum[1];
work();
}
printf("%d\n",cnt);
for(int i=1;i<=cnt;i++,puts(""))
for(int j=1;j<=n;j++){
printf("%d ",ans[i][j]);
}
}
T5 街灯
每个街灯上都有一个数,每次询问,第l个街灯到第r个街灯上的数模p等于v的有几个?
\(1 \le N,M \le 10^5\),街灯上的数不超过 \(10^4\), \(1 \le p \le 10^9\)。
发现有效的 \(p\) 最多为 \(10^4+1\) 。
考虑根号分治。
对于 \(p \le 100\) 我们预处理即可。
对于 \(p>100\) 我们考虑满足条件的数最多只有 \(100\) 种取值,我们不如直接开桶找有多少个数在区间 \([l,r]\) 中。
#include<bits/stdc++.h>
#include<cstdio>
#define lowbit(x) ((x)&(-x))
#define fir first
#define se second
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+50,M=1e4+50,maxn=1e4;
vector<int>tong[M];
int a[N];
vector<int> te[200][200];
int gt(int i,int x){
int l=0,r=tong[x].size()-1,ans=-1;
while(l<=r){
int mid=l+r>>1;
if(tong[x][mid]<=i)l=mid+1,ans=mid;
else r=mid-1;
}
return ans+1;
}
int gt(int l,int r,int x){
return gt(r,x)-gt(l-1,x);
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
tong[a[i]].push_back(i);
for(int i=1;i<=n;i++)
for(int j=1;j<=100;j++)
te[j][a[i]%j].push_back(i);
while(m--){
int l,r,p,v;int ans=0;
scanf("%d%d%d%d",&l,&r,&p,&v);
if(p<=100){
int t=upper_bound(te[p][v].begin(),te[p][v].end(),r)-lower_bound(te[p][v].begin(),te[p][v].end(),l);
printf("%d\n",t);
}
else {
for(int i=v;i<=maxn;i+=p)
ans+=gt(l,r,i);
printf("%d\n",ans);
}
}
}
模拟赛2
T1 数学题
令 \(A,B,C\) 为三个质数 \((A\le B\le C)\) , \(N=A\times B \times C\) 。
给出 \(N\) ,求 \(B\) 。
\(10 \le N \le 10^{14}\)
因式分解即可。
T2 子序列
给定一个长度为n的序列:\(a_1,a_2,\dots,a_n\) 。
要求你从中选出一个子序列,使得这个子序列的和对m取模后最大。
折半搜索,然后二分找最优答案,没了
\(1 \le n \le 35,0<m,a_1,a_2,\dots,a_n \le 10^9\) 。
T3 模
给出一个长度为n的数组 A(数组下标从1开始),和模数m 。有q次操作, 每次均是以下三种中的一个:
+ p r 表示将a[p]增加r ,并输出修改后的a[p] ;
- p r 表示将a[p]减少r ,如果a[p]<r则不执行减少r的操作(但还是要输出 ),并输出修改后的a[p] ;
s l r mod 询问在[l,r]区间中,所有在模m意义下值为mod的数的和。
\(1 \le n,q \le 10000,m \le 10 ,a_i \le 10000\)
\(m\) 很小,拿个树状数组维护一下即可(有小丑数据结构学傻了,写的线段树)。
T4 组队
小Z要将n名队员分组训练。
n 名队员每人都有一个默契值 a_i,由于 小Z和晋文公 一样懒,他也喜欢将一段连续的队员分成一组。
由于水是生命之源,在一个小组内如果有两个人的默契值乘积是一个平方数,那么这两个人就会划水,从而带动整个小组划水。这是 小Z不愿意看到的情况。
小Z会使用魔法将任意一个人的默契值改成任意整数,但这个技能最多能用k次。
小 想知道至少要分成多少组才不会有人划水。 注意:只有一个人的小组是不会划水的。
\(n \le 10^5,1 \le a_i \le 10^7, 0 \le k \le 20\) 。
不行,死去的记忆攻击我了,有小丑赛时闲的没事写了个哈希然后给写炸了。。。
考虑默契值乘积是个平方数。
这个要求好奇怪啊,让我们来玩一下。
首先来一波因式分解,看看在什么情况下他们的乘积是一个平方数。
当他们质因数分解每一个对应质数的指数和都为偶数时,他们是一个平方数。
偶数?奇偶性?那这不直接拿0,1表示就完了?
大概就是指数异或等于0就寄了。
然后有小丑真的去维护这玩意了。
实际上 \(a_i\) 只有 \(10^7\) 。我们将他的质因数分解的指数&1然后再恢复原来的数,开个桶,往里面扔就完事了。
判断解决了,套个dp完事。
#include<bits/stdc++.h>
#include<cstdio>
#define fir first
#define se second
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+50,M=1e7+50,maxn=460,maxm=1e7;
int prime[M],cnt;
int a[N];
bool vis[M];
int tot;
int flag[M];
int te[N][30];
int f[N][30];
signed main(){
int n,k;
scanf("%d%d",&n,&k);
for(int i=2;i<=maxm;i++){
if(!vis[i])prime[++cnt]=i;
for(int j=1;j<=cnt&&prime[j]<=maxm/i;j++){
vis[i*prime[j]]=1;
if(i%prime[j]==0)continue;
}
}
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++){
int t=a[i];ll tt=1;
for(int j=1;j<=maxn&&prime[j]<=t/prime[j];j++){
int cnt=0;
while(t%prime[j]==0){
t/=prime[j];
cnt++;
}
if(cnt&1)
tt*=prime[j];
}
if(t>1)
tt*=t;
a[i]=tt;
}
for(int i=0;i<=k;i++){
int cnt=0,l=1;
for(int r=1;r<=n;r++){
flag[a[r]]++;
if(flag[a[r]]>=2)cnt++;
while(cnt>i){
if(flag[a[l]]>=2)cnt--;
flag[a[l]]--;
l++;
}
te[r][i]=l;
}
while(l<=n){
flag[a[l]]--;
l++;
}
}
memset(f,0x3f,sizeof(f));
f[0][0]=0;
for(int i=1;i<=n;i++)
for(int j=0;j<=k;j++)
for(int t=0;t<=j;t++){
f[i][j]=min(f[i][j],f[te[i][t]-1][j-t]+1);
}
int ans=0x3f3f3f3f;
for(int i=0;i<=k;i++)ans=min(ans,f[n][i]);
printf("%d",ans);
}
T5 玩树
给你一棵树,点数为n ,第 个点的权值为a_i 。
定义一条路径 \(b_1,b_2,\dots,b_m\) 的权值是 \(\frac{\prod_{i=1}^m a_{b_i}}{m}\) 。
易得,一棵树有 \(\frac{n(n+1)}{2}\) 条路径,求这些路径权值的最小值。
注:任意两点之间都存在路径,所以一共有 \(\frac{n(n+1)}{2}\) 条路径 。
\(1 \le n \le 5\times 10^4,\sum n \le 5 \times 10^5,1\le a_i\le 10^9\)
这题题解写了好像也没有任何的启发,不会还是不会。
算了留着吧,以后再说
模拟赛3
T1 摆花
有一个花店,对于每一个非负美丽值,花店都有无数盆花。
我们需要从花店购买n盆花排成一排,对于花的排列一段区间 \([l,r]\),定义他的心动值为[l,r]中没出现过的最小非负整数。
我们需要最大化m个区间的心动值的最小值,输出这个数。
\(n,m \le 10^5\)
简单构造??
我们构造一个排列 \(0,1,2,3,n-1\),不断循环这个排列,可以发现这个就是最优答案。
因此答案为m个区间的最短区间长度,没了。
T2 打饭
有n个小朋友来食堂吃饭,他们排成长度为n的一个队伍。
小朋友看到别的小朋友比自己菜好会不高兴,两个小朋友i和j能互相看到对方的菜 当且仅当abs(i-j)=k ,产生的不高兴值是abs(a[i]-a[j]) ,a[i] 表示第 位小朋友菜丰盛的程度,换言之,如果菜的丰盛值按顺序排列是A ,那么产生的不高兴值为
如果小朋友产生的不高兴值和太大他们会哭,你现在有n盘菜,请你合理安排上菜 顺序,使得产生不高兴值的和最小,输出这个值。
\(n \le 3\times 10^5,k \le min(n-1,5000),-10^9\le A[i]\le 10^9\)
相当于分成 \(k\) 组,每组相邻两个小朋友可以互相看到。
对于每个组内,Ai一定是有序的,然后取模后的组特殊处理下即可。
套个dp完事。
然后我赛时套dp套出锅了,dp转移分两种,单个和分组,然后脑子不好写了个 \(nk\) 做法,有一堆冗余状态。
T3 小象砍树
给你一棵n个节点的带标号无根树。
每次,你可以选择一个度数为1的节点并将它从树上移除。问总共有多少种不同的 方式能将这棵树删到只剩1个点。 两种方式不同当且仅当至少有一步被删除的节点不同。
\(n \le 10^5\)
可以发现子树内的删点方法相互独立,就树形dp处理子树内的删点方法,合并,换根,没了。
T4 路径计数
勤劳的小蜜蜂生活在一棵树上,这棵树是完全二叉树(编号1~n ),编号为i的点\(\lfloor\frac{i}{2}\rfloor\)和编号为 的点有一条无向边(\(\lfloor\rfloor\)表示下取整)。
淘气的C想让蜜蜂迷路,所以又在树上加了m条无向边。
蜜蜂被搞得晕头转向,它们想知道,这个图上有多少条不同的简单路径。 简单路径指一条没有多次经过同一个点的路径(只有一个点的路径也是简单路径), 两条路径不同当且仅当经过的边集不同或经过边的顺序不同,这个答案可能很大,输 出对 取模的值。
注意重边也是不同的边。
\(n \le 10^9,m\le 10\)
简而言之,就是拿一个点表示下面的一棵子树,然后简单去下重,暴力dfs,没了
#include<bits/stdc++.h>
#define fir first
#define se second
using namespace std;
typedef long long ll;
const ll MOD=1e9+7;
const int N=1e5+50,M=2e5+50;
int head[N],nxt[M],to[M],num;
bool vis[N];
int sz[N];
map<int,int>tr;
int cnt=0;
int n,m;
void add(int u,int v){
++num;nxt[num]=head[u];to[num]=v;head[u]=num;
}
int gtsize(int u){
int sz=0;
int l=u,r=u;
while(l<=n){
sz+=min(r,n)-l+1;
l=l<<1;
r=r<<1|1;
}
return sz;
}
void update(int u){
if(tr.count(u<<1)){sz[tr[u]]-=sz[tr[u<<1]];update(u<<1);}
if(tr.count(u<<1|1)){sz[tr[u]]-=sz[tr[u<<1|1]];update(u<<1|1);}
}
ll dfs(int u){
ll sum=sz[u];
vis[u]=1;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(vis[v])continue;
(sum+=dfs(v))%=MOD;
}
vis[u]=0;
return sum;
}
int main(){
scanf("%d%d",&n,&m);
tr[1]=++cnt;
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
for(int k=u;k;k=k/2)
if(!tr[k])tr[k]=++cnt;
for(int k=v;k;k=k/2)
if(!tr[k])tr[k]=++cnt;
add(tr[u],tr[v]);add(tr[v],tr[u]);
}
for(auto t:tr){
if(t.fir!=1){
add(tr[t.fir],tr[t.fir/2]);
add(tr[t.fir/2],tr[t.fir]);
}
sz[t.se]=gtsize(t.fir);
}
update(1);
ll ans=0;
for(auto t:tr){
(ans+=dfs(t.se)*sz[t.se]%MOD)%=MOD;
}
printf("%lld",ans);
}
T5 游戏
S和C将要玩一个游戏。
这个游戏基于一个带权完全图, S会选择一个位置作为博物馆并在此位置等C来找,而C会被随机到一个位置去找 S,这个游戏很难认路, C只能事先在每个点设置一个路标,使得当C走到p这个点后,如果S不在这个点,他会继续走走到A_p的点,路标设置需要满足一个条件:从每个点开始沿着路标走必然能到达博物馆。一个点走到博物馆的代价定义为这个点沿路标走经过的路径,一条路径代价定义为经过的边权最小值 。
C马上要和S玩这个游戏了,他想做足功课,也就是如果他知道S会选择在第i个点时,他想要知道如何设置路标使得他到i的期望代价最小, C很聪明,他只需要你告诉当S选择第i个点时,从所有点到i的代价和。
\(n \le 3000\)
这题绝对不是一句话两句话能讲明白的,希望未来的我能理解吧(虽然题目原来的题解写的迷迷糊糊但是我实在不知道该怎么写的更好)
首先我们将所有边的边权减去最短边的边权。
显然我们只需要让其他点全部连到这条0边上,就能去掉所连点的价值。(见图1)
但是,如果i<-x的长度很长怎么办(见图2)
我们就要考虑拿出一部分点作为中介点,现在我们研究这些中介点与中介边的性质。
现在我们求这条链的贡献。
(性质1)我们可以发现这条链是递增的,如果他不是递增,则可以将递增的边合为一条,显然这更优(见图3)
在满足上面一行的前提下,我们可以发现,(性质2)链的贡献就是x到i的最短路径。
但是如果你仔细观察的话,会发现有一个特殊情况,他不是递增的(如图5)
这条特殊的路径最多包含2条边,否则会由性质1将后两条边合并成1条,这个令每个点初始 \(dis\) 为 \(\text{min}(edge[i][j])\times 2\) 即可。
初始化每个节点的 \(dis\) 为 \(\text{min}(edge[i][j])\times 2\) 。然后跑普通的 \(dij\) ,对于每个点答案为 \(dis[i]+(n-1)\times minW\) ,其中 \(minW\) 为边权最小值。
为什么这样做是对的?
首先,他处理了特殊情况。而对于一般性情况, \(x,y\) 的 \(dis\) 为 \(0\) ,然后相当于跑反图最短路。
模拟赛4
T1 奇怪的冰雹
轰隆轰隆,Z 国上空乌云密布,开始下起了冰雹。
现在有n个木桶在户外受到冰雹的破坏,已知最初每个木桶的完好程度为 \(a_i\) 。此次冰雹天气非常奇怪,总共分m轮降下冰雹,每轮只会降下一个 冰雹,等概率的砸到所有没有被摧毁的木桶上,被砸到的木桶的完好程度会减1 。 如果目前有k个没摧毁的木桶,每个木桶受到破坏的概率是\(\frac{1}{k}\) 。
当某个木桶的完好程度为0时,该木桶被摧毁,此后都不会再占用受到破坏的概率。如果所有木桶都被摧毁了,那么将没有木桶再受到破坏。
现在你的任务是,给定n,m和全部木桶的完好程度,问每个木桶在冰雹天气后没有 被摧毁的概率。
可以发现 \(n\) 只有4, \(a_i\) 只有50,不如直接开个dp数组,每一维存每个桶的完好程度,没了。
T2 完美划分
小Z拥有两个长度为n的浮点数数列A,B ,每个数列的元素之和为1。现在 小Z将两个数列上下对齐,然后同时将 A,B数列划分为的 段,保证每段内最少有一个数,且段内数列下标是连续的。例如n=4,k=3 时,可以将 A数列分成3段:{1,2},{3},{4} ; B也需要同样的划分, 3段同样为{1,2},{3},{4}: 。其中 1,2,3,4 表示的是数列中的第几个数。
现在小Z定义数列A,B每一段的幸运值为该段数字之和。即对于某段所在的区间为 [l,r],那么对于数列A该段的幸运值为\(A_l+A_{l+1}+\dots+A_r\);同理也可以计算出数列B该段的幸运值为\(B_l+B_{l+1}+\dots+B_r\) 。
该段的「特殊值」为A数列与B数列的幸运值之差的绝对值,即: \(|(A_l+A_{l+1}+\dots+A_r)-(B_l+B_{l+1}+\dots+B_r)|\)。 现在 小Z想要知道,怎么将A,B数列同时划分为连续的k段,才能保证每段的「特殊值」之和最大。请你帮小 计算出最大的「特殊值」之和。
dp,没了
T3 智能小球
小Z有一张包含n个节点的完全带权无向图,在0时刻,他会在图中选择一个节点,并在该节点放置一个“智能小球”,随后每1时刻智能小球会根据当前图的信息, 移动到其他节点处。已知小Z在0时刻时选择第i个节点的概率为\(p_i\) 。
假设在t时刻时,智能小球在节点i ,则在t+1时智能小球移动到节点j的概率为:
其中dis(i,j)表示节点i到节点j的最短路径的长度。
小Z想要知道T时刻时智能小球在每个节点的概率。
可以发现节点只有200个,但是T太大了,所以我们可以使用矩阵优化dp。
T4 运输货物
小Z要用n+1只骡子运送k种物资。每只骡子可以任选物资运输(也可以选择运输0种物资)。
由于骡子并不是马,所以没有任何一种物资能够同时被第0 ~ n-1只这n只骡子运输。
由于骡子并不是马,所以第1~n只这n只骡子并不能运输全部的k种物资。
根据以上 骡子并不是马原则,一共有多少种运输方案?
请给出答案对10^9+7取模的结果
T5 道路规划
小Z拥有一份Z国的国家地图,他发现Z国的城市布局非常奇怪,城市布局可以看作 是一个两行n列的网格状图(列下标从1开始)。如今城市之间缺少互通的道路, 现在Z国的领导人想要请小Z为城市之间修建双向通行的道路的方案做出最优的规划。
由于资金的限制, Z国领导人只想确保在某两列之间修建一些双向通行的道路让这 两列之间的所有城市能够相互到达即可。小Z已经了解到 Z国每一对相邻城市之间修 建道路的花费,所以小 能够通过这些信息计算出实现领导人的目的的最少花费。
但是现在还有一个更大的困难,随着时间的变化,在某些相邻城市之间修建双向通信 的道路的花费会发生改变,小Z需要在规划道路修建方案的时候及时处理这些变化。
由于Z国领导人之间在选择某两列的时候发生了分歧,所以Z国领导人会多次询问小 保证第i~j列的所有城市之间能够相互通行的最少花费是多少。
注:询问是遵循时间顺序的,随着时间的改变,某些相邻的城市之间修建道路的花费 也会发生改变。小Z在规划修建方案的时候,不能涉及到除i~j范围内的其他城市。
模拟赛5
T1 探险
这道题……有点难评价哈
一道剪枝题,但是我脑子不好(甚至8.26写博客时盯了半天才意识到死在哪里了)+运气好=赛时70分
暑假到了,你和你的朋友们想去野外探险。 你们去探险的地方是一片森林。这片森林可以抽象成一个 \(n\times m\) 的矩阵 。
如果 是 '#',表示 这个位置生长着树木;如果 是 '.',表示 这个位置是空地。 由于你非常激动,你每秒最多可以走k米。在每一秒内,你可以选择向上下左右其中一个方向移动。
当然,你移动的路径中只能包含空地,不能包含树木。 现在你在 \((x_1,y_1)\),你想到达终点 \((x_2,y_2)\) 。你最短在多少秒内能到达终点?
赛时脑子不好啥都没判,暴力vis数组甚至没加方向,但是凭着爆棚的rp骗了70分。
加了方向还是寄了,但是lhy同学帮我改了一发就没寄。
写博客的时候盯了半天代码,意识到如果使用vis+方向判断的话,可能当前点 \((x_1,y_1)\) 到另一个位置 \((x_3,y_3)\) 距离小于等于 \(k\) ,但是在 \((x_1,y_1)\) 到 \((x_3,y_3)\) 之间有一个点被 \((x_2,y_2)\) 更新了,跳出循环了。但是因为 \((x_2,y_2)\) 到 \((x_3,y_3)\) 的距离大于 \(k\) ,无法更新到 \((x_3,y_3)\) ,然后就寄了。
于是,代码应该是这个样子。
#include<bits/stdc++.h>
#include<cstdio>
#define fir first
#define se second
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1200;
int dis[N][N];
int dx[]={0,-1,0,1};
int dy[]={-1,0,1,0};
char s[N][N];
int sx,sy,tx,ty;
int n,m,k;
void bfs(){
memset(dis, 0x3f, sizeof dis);
queue<PII>q;
dis[sx][sy]=0;
q.push({sx,sy});
while(!q.empty()){
int x=q.front().fir,y=q.front().se;
q.pop();
if(x==tx&&y==ty){
printf("%d",dis[x][y]);
return;
}
for(int i=0;i<4;i++){
for(int t=1;t<=k;t++){
int xx=x+t*dx[i],yy=y+t*dy[i];
if(xx<1||yy<1||xx>n||yy>m)break;
if(s[xx][yy]=='#')break;
if(dis[xx][yy]<dis[x][y]+1)break;
if(dis[xx][yy]!=dis[x][y]+1)q.push({xx,yy});
dis[xx][yy]=dis[x][y]+1;
}
}
}
puts("-1");
return ;
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)
scanf("%s",s[i]+1);
scanf("%d%d%d%d",&sx,&sy,&tx,&ty);
bfs();
return 0;
}
T2 合成
给出一个长度为n的数组,执行下列操作:
找到最小的,至少出现了两次的数字 ,将第一次出现的x从数组中删除,将第二次 出现的x改为2*x。直到无法再进行这样的操作为止。
输出最后的数组。
对于每一次操作,至少删掉一个数字,模拟即可。
#include<bits/stdc++.h>
#include<cstdio>
#define fir first
#define se second
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef pair<ll,int> PII;
const ll INF = 1e18;
const int N=2e5+50;
multiset<PII>s;
PII a[N];
int cnt;
bool cmp(const PII &a,const PII &b){
return a.se<b.se;
}
int main(){
s.insert({INF,0});
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
ll x;
scanf("%lld",&x);
s.insert({x,i});
}
while(s.size()>1){
multiset<PII>::iterator t1=s.begin(),t2=s.begin();
t2++;
if((*t1).fir==(*t2).fir){
s.insert({2ll*(*t2).fir,(*t2).se});
s.erase(t1);s.erase(t2);
}else {
a[++cnt]=(*t1);
s.erase(t1);
}
}
sort(a+1,a+cnt+1,cmp);
printf("%d\n",cnt);
for(int i=1;i<=cnt;i++)printf("%lld ",a[i].fir);
return 0;
}
T3 健身
蒜头君每天会按 照某种顺序依次进行n个训练项目,编号分别为1~n 。 已知不同的训练顺序会影响训练的效果,现在蒜头君将训练项目进行量化(用数字表示训练效果,数字越大表示训练效果越好)。
当项目i被安排在项目j之前进行训练时,项目i可以获得的训练效果是 \(a_{i,j}\)。 为了使蒜头君的训练效果尽可能的好,请你帮助蒜头君确定训练的顺序,使得他可以 通过这 \(\frac{n(n-1)}{2}\) 对训练项目获得的训练效果之和最大。
状压板子题。
T4 顽皮的猴子
动物园中有n座小山,从1到n编号。n座小山通过 条双向道路连接。也就是说, n座小山形成了一棵树。
动物园中一共有m只猴子,编号从1~m到 。第i只猴子居住在第c_i座小山。请注意,一 座小山上可能不止一只猴子,也可能没有猴子。
这些猴子非常顽皮,所以动物园的管理员经常对猴子的位置进行询问,来确认它们不会乱跑。管理员一共会给出q个询问。在每个询问中,他都会给出数字 u、v 和k 。对于每次询问,你需要:
假设有t只猴子生活在从小山u到小山v的最短道路上。(因为 n 座小山形成了一棵 树,所以任何两座小山之间的最短路径都是唯一的。)假设这些猴子的编号依次是 \(p_1<p_2<\dots<p_t\) 。管理员想知道这t只猴子中前k小的编号是哪些。如果 \(t<k\), 那么管理员想知道路径上的所有猴子的编号。也就是说,令 \(ans=min(k,t)\),你需要输出 \(ans\) 以及 \(ans\)个猴子的编号: \(p_1,p_2,\dots,p_{ans}\) 。
可以发现 \(k\) 的范围很小,用数据结构维护前 \(10\) 小即可。
#include<bits/stdc++.h>
#include<cstdio>
#define fir first
#define se second
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+5,M=2e5+5,INF=0x3f3f3f3f;
class Queue {
public:
int a[12];
int ql,qr;
Queue() {memset(a,0,sizeof(a));ql=1,qr=0;}
void push(int x) {a[++qr]=x;}
void clear() {ql=1;qr=0;}
bool empty() {return ql>qr;}
int front() {return a[ql];}
int back() {return a[qr];}
void pop(){ql++;}
int size(){return qr-ql+1;}
};
int head[N],nxt[M],to[M],num;
int fa[N][18],dep[N];
Queue g[N][18],qwq[N];
vector<int>a[N];
int n,m;
void add(int u,int v) {
++num;
nxt[num]=head[u];
to[num]=v;
head[u]=num;
}
void pushup(Queue &qwq,Queue qwq1,Queue qwq2) {
int tot1=1,tot2=1;
qwq.clear();
for(int i=1; (!qwq1.empty()||!qwq2.empty())&&i<=10; i++) {
if(qwq2.empty())qwq.push(qwq1.front()),qwq1.pop();
else if(qwq1.empty())qwq.push(qwq2.front()),qwq2.pop();
else if(qwq1.front()<=qwq2.front())qwq.push(qwq1.front()),qwq1.pop();
else if(qwq1.front()>qwq2.front())qwq.push(qwq2.front()),qwq2.pop();
}
}
void dfs_(int u) {
if(!a[u].empty()) {
for(int i=0; i<a[u].size()&&i<10; i++)
qwq[u].push(a[u][i]);
}
for(int i=1; i<17; i++) {
fa[u][i]=fa[fa[u][i-1]][i-1];
pushup(g[u][i],g[fa[u][i-1]][i-1],g[u][i-1]);
}
for(int i=head[u]; i; i=nxt[i]) {
int v=to[i];
if(v==fa[u][0])continue;
dep[v]=dep[u]+1;
fa[v][0]=u;
g[v][0]=qwq[u];
dfs_(v);
}
}
Queue LCA(int u,int v) {
if(dep[u]<dep[v])swap(u,v);
Queue ans=qwq[u];
for(int i=16; i>=0&&dep[u]>dep[v]; i--)
if(dep[fa[u][i]]>=dep[v]){
pushup(ans,g[u][i],ans);
u=fa[u][i];
}
if(u==v)return ans;
pushup(ans,qwq[v],ans);
for(int i=16; i>=0; i--) {
if(fa[u][i]!=fa[v][i]){
pushup(ans,g[u][i],ans);
pushup(ans,g[v][i],ans);
u=fa[u][i],v=fa[v][i];
}
}
pushup(ans,g[u][0],ans);
return ans;
}
int main() {
int q;
scanf("%d%d%d",&n,&m,&q);
for(int i=1; i<n; i++) {
int u,v;
scanf("%d%d",&u,&v);
add(u,v);
add(v,u);
}
dep[1]=1;
for(int i=1; i<=m; i++) {
int x;
scanf("%d",&x);
a[x].push_back(i);
}
dfs_(1);
while(q--) {
int u,v,k;
scanf("%d%d%d",&u,&v,&k);
Queue ans=LCA(u,v);
printf("%d ",min(ans.size(),k));
while(!ans.empty()&&k--)printf("%d ",ans.front()),ans.pop();
puts("");
}
return 0;
}
T5 咕咕咕
留坑待填
模拟赛6
T1 幸运数字II
问在区间 \([L,R]\) 中符合下列条件的数的个数
- \(x\) 是质数
- \(x\) 是两个质数的乘积
线性筛筛一下即可。
T2 小树精灵
在一棵树上放置 3 个精灵,使他们距离相等
显然他们之间的路径有一个焦点 \(p\) ,点 \(p\) 到三点的距离相等。
因为路径要交于点 \(p\) ,所以一定在 \(p\) 的不同的子树内。
我们考虑枚举 \(p\) 统计在不同子树内到点 \(p\) 距离为 \(k\) 的点的个数。
大概就是统计每个孩子节点内,深度为 \(k\) 的点的个数,然后对于每个 \(k\) 做个容量为3的01背包。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=3e3+50;
int cnt[N];
ll t1[N],t2[N],t3[N];
vector<int>e[N];
ll ans;
void dfs(int u,int fa,int dep){
cnt[dep]++;
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
if(v==fa)continue;
dfs(v,u,dep+1);
}
}
int main(){
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
if(x)e[x].push_back(i);
if(x)e[i].push_back(x);
}
for(int i=1;i<=n;i++){
memset(t1,0,sizeof(t1));
memset(t2,0,sizeof(t2));
memset(t3,0,sizeof(t3));
for(int j=0;j<e[i].size();j++){
memset(cnt,0,sizeof(cnt));
int v=e[i][j];
dfs(v,i,1);
for(int k=1;k<=n;k++){
t3[k]+=t2[k]*cnt[k];
t2[k]+=t1[k]*cnt[k];
t1[k]+=cnt[k];
}
}
for(int i=1;i<=n;i++)ans+=t3[i];
}
printf("%lld",ans);
}
T3 滑道
蒜头君有n根竖着的滑道、m根横着的滑道。竖着的滑道在空地上并排放置,编号为 1,2,3,...,n。每根竖着的滑道上方最初有一个小球,每个小球上有一个编号, 小球的编号为当前所在竖着滑道的编号。
横着的滑道是用来连接两根相邻的竖着滑道的,不同的是,每根横着的滑道所在的高度均不相同。
接下来小球会依次从顶端沿着竖着的滑道开始向下滑落,在滑落的过程中,如果遇到 横着的滑道时,会滑向横着滑道的另一端,然后继续向下滑落,直到滑落到最低点。 图中红色线表示1号小球向下滑落的轨迹。
蒜头君想要完成两个任务:
- 通过给定的 根竖着的滑道和 根横着的滑道构成的结构,求出每个小球滑落到最低点时,最底端由小球编号构成的序列,如图中的序列为:4,2,5,6,1,3 。
- 如果重新选择一些横着的滑道,并按照最优的方法连接两根相邻的竖着的滑道, 使得获得的最终序列同样能够达到上面的效果,那么最少需要多少根横着的滑道?
看完题面第一反应,小球难道不会落到同一点上吗?
然后就开始证明,然后就没然后了,知道该怎么做了。
对于一根横着的管道,本质上是交换两个相邻的小球,然后就没了。
第一问是暴力交换,第二问是逆序对。
然后,我考场就把逆序对板子写寄了。
这题告诉我们要从看起来离谱的地方开始突破。
#include<bits/stdc++.h>
#include<cstdio>
#define fir first
#define se second
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+50;
int a[N],b[N];
ll ans;
void dfs(int l,int r){
if(l==r)return;
int mid=l+r>>1;
dfs(l,mid);dfs(mid+1,r);
int pos1=l,pos2=mid+1,pos=l;
while(pos1<=mid&&pos2<=r){
if(a[pos1]<a[pos2])b[pos++]=a[pos1++];
else b[pos++]=a[pos2++],ans+=mid-pos1+1;
}
while(pos1<=mid)b[pos++]=a[pos1++];
while(pos2<=r)b[pos++]=a[pos2++];
for(int i=l;i<=r;i++)a[i]=b[i];
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)a[i]=i;
for(int i=1;i<=m;i++){
int x;
scanf("%d",&x);
swap(a[x],a[x+1]);
}
for(int i=1;i<=n;i++)printf("%d ",a[i]);puts("");
dfs(1,n);
printf("%lld",ans);
return 0;
}
T4 Dove 的疑惑
留坑,优先填。
T5 K直径生成树
留坑待填
模拟赛7
T1 序列
给你一个初始值全是0的 n 个元素的序列,你要对这个序列做 m 次操作,操作有两 种:
1 l r,将序列中 到 个元素全部加1。2 l r,将 \(l\) 到 \(r\) 个操作再做一遍。保证 \(l,r\) 小于这个操作的编号。
考虑从后往前扫描操作序列,记录当前位置需要执行多少次。
然后维护差分序列,没了。
T2 消息传递
有一棵树,你可以在1时刻选定一个点染色,在接下来的每一个时间点内,在每一个时刻内每一个已经被染色的节点都可以选定连接他的一个节点进行染色。
问所有点染色的最短时间和在保证时间最短的前提下,有哪些点可以首先(在1时刻)被染色。
显然对于一个节点,同时处理向上或向下染色太难了,不如直接将最先染色的点定为根,每个点只能被他的父亲节点染色。
树形dp是很简单的,将孩子节点按照所需时间从大到小排序,合并即可。
换根也是暴力换就行,没啥特别的。
关于考场没切原因是没排序这件事。
#include<bits/stdc++.h>
#define fir first
#define se second
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+50;
struct Edge{
int v,val;
bool operator<(const Edge &b)const{
return val<b.val;
}
};
vector<Edge>e[N];
vector<int>answer;
int f[N];
int n,ans=1e9;
int dfs1(int u,int fa){
for(int i=0;i<e[u].size();i++){
int v=e[u][i].v;
if(v==fa){
e[u][i]={fa,0};
continue;
}
e[u][i]={v,dfs1(v,u)};
}
int ans=0;
sort(e[u].begin(),e[u].end());
for(int i=(fa?1:0),sz=e[u].size();i<sz;i++)
ans=max(ans,(int)e[u][i].val+sz-i);
return ans;
}
void dfs2(int u,int fa){
int pre[e[u].size()+2],suf[e[u].size()+2];
for(int i=0;i<e[u].size();i++){
int v=e[u][i].v;
if(v==fa){
e[u][i]={fa,f[fa]};
break;
}
}//给父节点找个位置
sort(e[u].begin(),e[u].end());
suf[e[u].size()]=0;
pre[0]=(int)e[u][0].val+e[u].size();
for(int i=1,sz=e[u].size();i<sz;i++)//防越界
pre[i]=max(pre[i-1],(int)e[u][i].val+sz-i);
for(int i=e[u].size()-1,sz=e[u].size();i>=0;i--){
suf[i]=max(suf[i+1],(int)e[u][i].val+sz-i);
}
if(suf[0]<ans){
ans=suf[0];
answer.clear();
answer.push_back(u);
}
else if(ans==suf[0])answer.push_back(u);
for(int i=0;i<e[u].size();i++){
int v=e[u][i].v;
if(v==fa)continue;
if(i)f[u]=max(pre[i-1]-1,suf[i+1]);
else f[u]=suf[i+1];
dfs2(v,u);
}
}
void work1(){
int ans=1e9;
for(int i=1;i<=n;i++){
int t=dfs1(i,0);
if(t<ans){
ans=t;
answer.clear();
answer.push_back(i);
}
else if(ans==t)answer.push_back(i);
}
printf("%d\n",ans+1);
for(int i=0;i<answer.size();i++)printf("%d ",answer[i]);
}
void work2(){
dfs1(1,0);
dfs2(1,0);
printf("%d\n",ans+1);
sort(answer.begin(),answer.end());
for(int i=0;i<answer.size();i++)printf("%d ",answer[i]);
}
int main(){
scanf("%d",&n);
for(int i=2;i<=n;i++){
int x;
scanf("%d",&x);
e[i].push_back({x,0});
e[x].push_back({i,0});
}
if(n<=1e3)work1();//!
else work2();
return 0;
}
T3 区间
有 \(n\) 个区间,第 \(i\) 个区间是 \([l_i,r_i]\) ,它的长度是 \(r_i-l_i\) 。
有 \(q\) 个询问,每个询问给定 \(L,R,K\) ,询问被 \([L,R]\) 包含的且长度不小于 \(K\) 的区间 数量。
这道题其实也挺好的,运用了一个重要的性质,不被 \([L,R]\) 包含的区间只会满足且至少满足下面的一个条件:
- \(l\in [1,L-1]\)
- \(r\in [r+1,n]\)
- \([l,r]\) 的长度大于 \([L,R]\) 的长度。
排个序,然后拿树状数组统计即可。
留个坑,改天用CDQ来写一写这道题。
#include<bits/stdc++.h>
#define fir first
#define se second
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=5e5+50;
struct RANGE{
int l,r,len;
bool operator< (const RANGE &b){
return len<b.len;
}
}range[N];
struct Ques{
int l,r,k,id,t;
bool operator< (const Ques &b){
return k<b.k;
}
}ques[2*N];
int ans[N],c1[N],c2[N];
int n,q;
void add(int x,int i,int c[]){
while(i<=n){
c[i]+=x;
i+=lowbit(i);
}
}
int query(int i,int c[]){
if(i<0)return 0;
int ans=0;
while(i){
ans+=c[i];
i-=lowbit(i);
}
return ans;
}
int main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++){
scanf("%d%d",&range[i].l,&range[i].r);
range[i].len=range[i].r-range[i].l;
}
sort(range+1,range+n+1);
for(int i=1;i<=q;i++){
int l,r,k;
scanf("%d%d%d",&l,&r,&k);
if(r-l<k)continue;
ques[i]={l,r,r-l,i,1};
ques[i+q]={l,r,k-1,i,-1};
}
sort(ques+1,ques+2*q+1);
for(int i=1,j=1;i<=2*q;i++){
while(j<=n&&range[j].len<=ques[i].k){
add(1,range[j].l,c1);
add(1,range[j].r,c2);
j++;
}
ans[ques[i].id]+=(j-query(ques[i].l-1,c1)-(query(n,c2)-query(ques[i].r,c2)))*ques[i].t;
}
for(int i=1;i<=q;i++)printf("%d\n",ans[i]);
return 0;
}
T4 迷宫
留个坑
T5 水
你在我的世界里,开辟了一个n*m的区域,每个格子面积相同,格子内的土地的海拔为\(h_{i,j}\) 。外围的土地可以被视作拥有足够高的海拔,现在下了大雨,水淹没了这个区域的最高点。你决定放置k个海绵(假设海绵不占空间)到一些格子,海绵 可以吸走该格子内以及流入该格子的所有水。你每次只放置一个海绵,而为了尽快吸干这些水,你想要最小化剩余的积水的体积。(使一个格子的海拔升高 1 的水的体 积为 1 单位体积)你想知道,在最优的方案下,对于所有的 \(i\) ,第 \(i\) 次 放置后的积水还剩多少单位体积? 你的方案应该先最优化第 1 次放置后的剩余体积,再最优化第 2 次放置后的剩余体 积,依次类推。由于输出比较大,你只需要每个剩余积水的异或和即可。
\(1\le n,m\le 500,1\le K \le n\times m,1\le h_{i,j} \le 10^6\)
我们考虑比他更低的连通块可以吸走当前位置的水,我们从当前位置向更低的连通块连边,表示连通块可以吸走当前位置的水。
我们连边时将权值设为 \((父亲高度-自己高度)\times 自己的点数\) ,每次放置海绵是沿着一条链吸干水,然后找 \(k\) 条不交的长链,所以我们采取类似长链剖分的方式查找。
#include<bits/stdc++.h>
#define fir first
#define se second
using namespace std;
typedef pair<int,int> PII;
typedef long long ll;
const int N=510;
int head[N*N],nxt[N*N*2],to[N*N*2],W[N*N*2],num;
int h[N][N],sz[N*N];
PII pos[N*N];
int posx[N*N],posy[N*N];
int fa[N*N];
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
int hson[N*N];
ll d[N*N];
ll ans[N*N],cnt;
ll S=0;
bool cmp(const PII &a,const PII &b){
return h[a.fir][a.se]<h[b.fir][b.se];
}
void add(int u,int v,int w){
++num;nxt[num]=head[u];to[num]=v;W[num]=w;head[u]=num;
}
int find(int x){
if(fa[x]==x)return x;
return fa[x]=find(fa[x]);
}
void dfs(int u){
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
dfs(v);
d[v]+=W[i];
d[u]=max(d[u],d[v]);
if(d[v]>d[hson[u]])hson[u]=v;
}
}
void dfs(int u,int tp){
// printf("%d\n",u);
if(tp==u)ans[++cnt]=d[u];
if(hson[u])dfs(hson[u],tp);
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==hson[u])continue;
dfs(v,v);
}
}
bool cmp2(const ll &a,const ll &b){
return a>b;
}
int main(){
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&h[i][j]);
pos[(i-1)*m+j]={i,j};
posx[(i-1)*m+j]=i;
posy[(i-1)*m+j]=j;
}
for(int i=1;i<=n*m;i++)fa[i]=i;
sort(pos+1,pos+n*m+1,cmp);
for(int i=1;i<=n*m;i++){
int x=pos[i].fir,y=pos[i].se;
sz[(x-1)*m+y]=1;
S+=h[pos[n*m].fir][pos[n*m].se]-h[x][y];
for(int j=0;j<4;j++){
int xx=x+dx[j],yy=y+dy[j];
if(xx<1||yy<1||xx>n||yy>m)continue;
int fx=find((x-1)*m+y),fy=find((xx-1)*m+yy);
if(!sz[fy])continue;
if(fx!=fy){
sz[fx]+=sz[fy];
fa[fy]=fx;
add(fx,fy,sz[fy]*(h[x][y]-h[posx[fy]][posy[fy]]));
}
}
}
int rt=(pos[n*m].fir-1)*m+pos[n*m].se;
dfs(rt);
dfs(rt,rt);
ll qwq=0;
sort(ans+1,ans+cnt+1,cmp2);
for(int i=1;i<=k;i++){
S-=ans[i];
qwq^=S;
}
printf("%lld",qwq);
}
模拟赛8
T1 立方体
在n维空间中,一个单位立方体由 \(2^n\) 个点组成。
他们的坐标形如 \((x_1,x_2,\dots,x_n)\)。 定义n维空间中两点的距离为曼哈顿距离,点 \(p(p_1,p_2,\dots,p_n)\) 与点 \(q(q_1,q_2,\dots,q_n)\) 的距离为 \(\sum_{i=1}^n|p_i-q_i|\) 。
现在给你单位立方体上一点 \(p\) 以及一个整数 \(k\) ,问你与点 \(p\) 距离为 \(k\) 的单位立方体 上点的数量。
因为这样的点可能很多,所以请对 \(10^9+7\) 取模。
二进制与组合水题, \(C_n^k\) ,没了。
T2 函数最值
对于一个数组 \(A\) 定义 \(F(A)=max\{abs(a_i-a_{i+1})\}\)
给定一个数组,最多修改其中 \(k\) 个元素(只能把数字修改为整数),求 \(F(A)\) 的最小值
最大值最小,显然可以二分,二分再套一个 \(dp\) 即可切掉本题。
但是问题来了,我考场上不会写……于是写了个 \(n^3\) 暴力
考场上没测边界 \(k=0\) 所以挂了,下面是修改后的考场代码
#include<bits/stdc++.h>
#define fir first
#define se second
#define lobit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e3+50;
int f[N][N];//f[i][j],到i为止,修改次数为j的最小函数值
int a[N];
int gtabs(int x){
return max(x,-x);
}
int calc(int i,int j,int k){
if(i==0||j==0)return 0;
k++;
int t=gtabs(a[i]-a[j]);
if(t%k==0)return t/k;
return t/k+1;
}
int main(){
int n,k;
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
memset(f,0x3f,sizeof(f));
for(int i=0;i<=k;i++)f[i][i]=0;
for(int i=1;i<=k;i++)f[i][i-1]=0;
int ans=2e9;
if(k==0){
int ans=0;
for(int i=2;i<=n;i++)ans=max(ans,calc(i-1,i,0));
printf("%d",ans);
return 0;
}
for(int i=2;i<=n;i++)
for(int j=0;j<=i&&j<=k;j++)
for(int k=0;k<=j;k++){
if(k==i)continue;
f[i][j]=min(f[i][j],max(f[i-k-1][j-k],calc(i-k-1,i,k)));
}
for(int i=0;i<=k;i++)ans=min(ans,f[n-i][k-i]);
printf("%d",ans);
return 0;
}
下面是正解,思路大概是二分答案,然后使用dp检查是否能够满足。
实际上,就是我的 \(n^3\) 暴力将状态与储存的值交换后进行二分与dp。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+50;
int a[N];
int f[N];
int n,k;
int gtabs(int x){
return max(x,-x);
}
int gtdis(int i,int j){
if(i==0||j==0)return 0;
return gtabs(a[i]-a[j]);
}
bool check(int mid){
for(int i=0;i<=n;i++)f[i]=0x3f3f3f3f;
f[0]=f[1]=0;
for(int i=2;i<=n;i++){
for(int j=0;j<i;j++)
if(gtdis(i,j)<=(i-j)*mid)
f[i]=min(f[i],f[j]+(i-j-1));
}
for(int i=0;n-i>0&&i<=k;i++)
if(f[n-i]<=k-i)return true;
return false;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
int l=0,r=1000000000,ans=-1;
while(l<=r){
int mid=l+r>>1;
if(check(mid))r=mid-1,ans=mid;
else l=mid+1;
}
printf("%d",ans);
}
T3 城市
在坐标轴上有 \(N\) 个城市。给出每个城市的人口。一个城市的父节点定义为:人口比当前城市多,而且离当前城市最近的城市。如果有多个这样的城市,则父节点为人数多的那一个。 保证每个城市的位置和人数不同。 问每个城市的父节点是哪一个城市?
单调栈的板子题,从前往后扫一遍,从后往前扫一遍,没了
T4 捉迷藏
有一颗 n 个节点的无根树,每个节点上有一盏灯,给定灯的初始状态。
在这棵树上移动,每到达一个节点点亮一盏灯,注意原来已经点亮的灯不会被再次点亮。
问从每个点出发,在保证移动过程中点亮灯数为偶数的前提下,最多能到达的点的数量。
显然的,如果未点亮的灯为偶数个,那么全点亮即可(下面就不讨论这种情况,默认未点亮的灯为奇数个)
显然的,每栈没亮着的灯将图分成若干个连通块。对于每个点只有一个连通块没有访问。
考虑没点亮的灯 \(u\) 对于其他节点的贡献。
我们枚举 \(u\) 使他为分界点,使两个连通块间互相无法抵达。
对于 \(u\) 节点划分的每一个连通块都只能访问到自己内部的节点,我们要将 \(u\) 对每个节点的贡献传递给每个节点上去。
对于 \(u\) 的子树,为从上向下传递,这个好传,只要在 \(u\) 的孩子节点打个标记,在dfs时下传并合并标记即可。
对于 \(u\) 的祖先节点,兄弟节点,我们需要先上传标记再下传标记,注意,u的孩子节点不会接收到下传标记,需要特殊处理下。
这题最重要的或许是从分解点的角度上考虑问题。
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+50,M=2e6+50;
int head[N],nxt[M],to[M],num;
int a[N],ans[N],tag1[N],tag2[N];
int sz[N];
int n,sum=0;
void add(int x,int y){
++num;nxt[num]=head[x];to[num]=y;head[x]=num;
}
void dfs(int u,int fa){
sz[u]=1;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==fa)continue;
dfs(v,u);
sz[u]+=sz[v];
if(a[u]==0) tag2[v]=max(tag2[v],sz[v]);
}
if(a[u]==0) tag1[u]=max(tag1[u],n-sz[u]);
}
void dfs1(int u,int fa){//上传
int res1=0,res2=0;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==fa)continue;
dfs1(v,u);
ans[u]=max(ans[u],tag1[v]);
tag1[u]=max(tag1[u],tag1[v]);
res2=max(res2,tag1[v]);
if(res2>res1)swap(res1,res2);
}
for(int i=head[u];i;i=nxt[i]){//特殊处理并与下传标记合并
int v=to[i];
if(v==fa)continue;
if(tag1[v]!=res1)tag2[v]=max(tag2[v],res1);
else tag2[v]=max(tag2[v],res2);
}
}
void dfs2(int u,int fa){//下传
ans[u]=max(ans[u],tag2[u]);
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==fa)continue;
tag2[v]=max(tag2[v],tag2[u]);
dfs2(v,u);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]),sum=sum^a[i]^1;
if(sum==0){
for(int i=1;i<=n;i++)printf("%d\n",n);
return 0;
}
for(int i=1;i<n;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);add(y,x);
}
dfs(1,0);
dfs1(1,0);
dfs2(1,0);
for(int i=1;i<=n;i++)
printf("%d\n",ans[i]);
}
T5 Cicada 的序列
对于这道题,我的评价是:zpl tql!
给你一个长度为n的序列A。
对于该序列的一个连续子序列 \(a_l,a_{l+1},\dots,a_r\) 来说,权值为\(a_l \bmod a_{l+1} \bmod a_{l+2} \bmod \dots\bmod a_r\) 。 这个序列的所有连续子序列的权值和是多少。
取模最重要的性质是对于一个数 \(x\) ,有效的取模操作最多只会进行 \(log\) 次。
对于一个数 \(x\) ,被一个比他大的数取模是没有用处的
对于取模不符合交换律。
从后往前扫描整个数组,维护一个单调栈,对于栈内的每个数,从栈顶至栈底,下标从小到大,数字从大到小。
对于一个数字 \(x\) 从栈顶到栈底找到第一个比他小的数字进行取模,找到的数字是第一个有效取模,重复进行直到无法进行有效取模。
#include<bits/stdc++.h>
#define fir first
#define se second
using namespace std;
typedef pair<int,int> PII;
typedef long long ll;
const int N=3e5+50;
int a[N];
PII st[N];int top;
ll sum=0;
int read(){
int x=0;char c=getchar();
while(c<'0'||c>'9')c=getchar();
while(c>='0'&&c<='9'){
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return x;
}
int main(){
int n;
n=read();
for(int i=1;i<=n;i++)a[i]=read();
for(int i=n;i>=1;i--){
while(top&&a[i]<st[top].fir)top--;
int x=a[i],lst=i,t=top;
while(true){
int l=1,r=t,ans=-1;
while(l<=r){
int mid=l+r>>1;
if(st[mid].fir<=x)l=mid+1,ans=mid;
else r=mid-1,t=mid-1;
}
if(ans==-1)break;
sum+=1ll*x*(st[ans].se-lst);
x%=st[ans].fir;
lst=st[ans].se;
}
sum+=1ll*x*(n-lst+1);
st[++top]={a[i],i};
}
printf("%lld",sum);
}
模拟赛9
T1 三角田地
给你一些点,问他们能够组成的直角三角形的面积的和。对1e9+7取模
\(N \le 10^5, -10^4 \le X_i,Y_i\le 10^4\)
好好好赛时没取模,爆炸!
做法大概就是把同行的丢树状数组里,算一下贡献,再把同列的丢树状数组里,算一下贡献
#include<bits/stdc++.h>
#include<cstdio>
#define fir first
#define se second
#define MOD 1000000007
#define lowbit(x) ((x)&(-x))
using namespace std;
typedef long long ll;
typedef pair<pair<ll,ll>,ll> PIII;
const int N=1e5+50;
PIII a[N];
ll c1[N],c2[N];
bool cmp2(const PIII &a,const PIII &b){
return a.fir.se<b.fir.se;
}
void add(ll c[],ll x,ll i){
if(!i)return;
while(i<=20010){
(c[i]+=x)%=MOD;
i+=lowbit(i);
}
}
ll query(ll c[],ll i){
if(!i)return 0;
ll ans=0;
while(i){
(ans+=c[i])%=MOD;
i-=lowbit(i);
}
return ans;
}
int main(){
int n;ll ans=0;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld%lld",&a[i].fir.fir,&a[i].fir.se);
a[i].fir.fir+=10001;a[i].fir.se+=10001;
}
sort(a+1,a+n+1);
for(int i=1;i<=n;i++){
int l=i,r=i;
while(r<n&&a[r+1].fir.fir==a[l].fir.fir)r++;
for(int i=l;i<=r;i++){
add(c1,a[i].fir.se,a[i].fir.se);
add(c2,1,a[i].fir.se);
}
for(int i=l;i<=r;i++){
(a[i].se+=1ll*query(c2,a[i].fir.se)*a[i].fir.se-query(c1,a[i].fir.se)%MOD)%=MOD;
(a[i].se+=1ll*(query(c1,20001)-query(c1,a[i].fir.se))-(query(c2,20001)-query(c2,a[i].fir.se))*a[i].fir.se%MOD)%=MOD;
}
for(int i=l;i<=r;i++){
add(c1,-a[i].fir.se,a[i].fir.se);
add(c2,-1,a[i].fir.se);
}
i=r;
}
sort(a+1,a+n+1,cmp2);
for(int i=1;i<=n;i++){
int l=i,r=i;
while(r<n&&a[r+1].fir.se==a[l].fir.se)r++;
for(int i=l;i<=r;i++){
add(c1,a[i].fir.fir,a[i].fir.fir);
add(c2,1,a[i].fir.fir);
}
for(int i=l;i<=r;i++){
(ans+=(1ll*query(c2,a[i].fir.fir)*a[i].fir.fir-query(c1,a[i].fir.fir))*a[i].se)%=MOD;
(ans+=(1ll*(query(c1,20001)-query(c1,a[i].fir.fir))-(query(c2,20001)-query(c2,a[i].fir.fir))*a[i].fir.fir)*a[i].se)%=MOD;
}
for(int i=l;i<=r;i++){
add(c1,-a[i].fir.fir,a[i].fir.fir);
add(c2,-1,a[i].fir.fir);
}
i=r;
}
printf("%lld",(ans+MOD)%MOD);
return 0;
}
T2 签到题
给定一棵 \(N\) 个点的无根树,每个点有一个权值 \(A_i\) ,需要你选定一个起点 ,从这个点出发对树进行深度优先遍历,得到一个DFS 序, 使得代价和 \(S=\sum_i^n i\times A_i\) 最小。
首先考虑两个点的情况
设 \(f_u\) 为只考虑 \(u\) 这棵字数内部的贡献。
当 \(v_1\) 在前 \(v_2\) 在后时,贡献为 \(f_{v_1}+f_{v_2}+size_{v_1}\times sum_{v_2}\)
当 \(v_2\) 在前 \(v_1\) 在后时,贡献为 \(f_{v_1}+f_{v_2}+size_{v_2}\times sum_{v_1}\)
当 \(v_1\) 在前更优时 \(size_{v_1}\times sum_{v_2}<size_{v_2}\times sum_{v_1}\)
所以在 \(\frac{size_{v_1}}{sum_{v_1}}<\frac{size_{v_2}}{sum_{v_2}}\) 时, \(v_1\) 在前更优
我们首先按照 \(\frac{sum}{f}\) 从小到大排序,首先插入的两点是 \(v_1,v_2\)
考虑再加入一个点 \(v_3\)
显然 \(\frac{size_{v_1}}{sum_{v_1}} \le \frac{size_{v_2}}{sum_{v_2}} \le \frac{size_{v_3}}{sum_{v_3}}\)
当 \(v_3\) 插在 \(v_1,v_2\) 前后时,我们可以先将 \(v_1,v_2\) 合并为一个大点 \(v\)
\(size_v=size_{v_1}+size_{v_2}\) , \(sum_v=sum_{v_1}+sum_{v_2}\)
所以 \(v_3\) 必定插在 \(v_1,v_2\) 之后
现在我们考虑 \(v_3\) 插在 \(v_1,v_2\) 之间
插在中间,贡献为 \(f_{v_1}+f_{v_2}+f_{v_3}+size_{v_1}\times (sum_{v_2}+sum_{v_3})+size_{v_3} \times sum_{v_2}\)
插在最后,贡献为 \(f_{v_1}+f_{v_2}+f_{v_3}+size_{v_1}\times (sum_{v_2}+sum_{v_3})+size_{v_2} \times sum_{v_3}\)
两式相减 \(size_{v_3}\times sum_{v_2}-size_{v_2}\times sum_{v_3}\)
因为 \(\frac{size_{v_1}}{sum_{v_1}} \le \frac{size_{v_2}}{sum_{v_2}} \le \frac{size_{v_3}}{sum_{v_3}}\)
所以 \(size_{v_3}\times sum_{v_2}-size_{v_2}\times sum_{v_3}>0\)
所以插在最后更优。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+50;
vector<int>e[N];
ll a[N],sum[N];
ll f[N];
ll sz[N];
ll ans=1e18;
int n;
bool cmp(const int &a,const int &b){
return 1ll*sz[a]*sum[b]<1ll*sz[b]*sum[a];
}
void dfs(int u,int fa){
f[u]=a[u];sz[u]=1;
sum[u]=a[u];
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
if(v==fa)continue;
dfs(v,u);
sz[u]+=sz[v];
sum[u]+=sum[v];
f[u]+=f[v];
}
sort(e[u].begin(),e[u].end(),cmp);
ll szS=1;
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
if(v==fa)continue;
f[u]+=szS*sum[v];
szS+=sz[v];
}
}
void dfs2(int u,int fa){
sort(e[u].begin(),e[u].end(),cmp);
ll suf[e[u].size()+1];
suf[e[u].size()]=0;
ll szS=1;
f[u]=a[u];sum[u]=a[u];
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
f[u]+=f[v]+szS*sum[v];
sum[u]+=sum[v];
szS+=sz[v];
}
ll t1=f[u],t2=sum[u],t3=sz[u];ans=min(ans,f[u]);
for(int i=e[u].size()-1;i>=0;i--){
int v=e[u][i];
suf[i]=suf[i+1]+sum[v];
}
szS=1;
for(int i=0;i<e[u].size();i++){
int v=e[u][i];
if(v==fa){
szS+=sz[v];
continue;
}
f[u]=t1-szS*sum[v]-sz[v]*suf[i+1]-f[v];
sum[u]=t2-sum[v];
szS+=sz[v];
sz[u]=n-sz[v];
sz[v]=n;
dfs2(v,u);
sz[u]=t3;
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n-1;i++){
int x,y;
scanf("%d%d",&x,&y);
e[x].push_back(y);
e[y].push_back(x);
}
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
dfs(1,0);
dfs2(1,0);
printf("%lld",ans);
}
彩蛋:博客代码都写完了,然后发现式子推炸了
彩蛋*2:中间数组(suf)没开long long导致调了半个小时
T3
我们称一张无向图是仙人掌,当且仅当这张无向图连通且每条边最多属于一个简单环。我们称一张无向
图是沙漠,当且仅当这张无向图中所有连通子图都是仙人掌。
给出一个N个点,M条边的沙漠,你可以删去其中的K条边。求能分成的连通块数量最大值。
优先删树边,优先删大环,没了
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+50,M=4e6+50;
int head[N],nxt[M],to[M],num=1;
int dfn[N],low[N],dep[N],cnt;
int ans;
int tree;
vector<int>ring;
void add(int u,int v){
++num;nxt[num]=head[u];to[num]=v;head[u]=num;
}
void dfs(int u,int fa){
dfn[u]=low[u]=++cnt;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(i^fa^1){
if(!dfn[v]){
dep[v]=dep[u]+1;
dfs(v,i);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u])tree++;
}else {
low[u]=min(low[u],dfn[v]);
if(dep[u]>dep[v])ring.push_back(dep[u]-dep[v]+1);
}
}
}
}
int main(){
int n,m,q;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
ans++;
dep[i]=1;
dfs(i,0);
}
}
if(q<=tree){
ans+=q;
printf("%d",ans);
return 0;
}
ans+=tree;
q-=tree;
sort(ring.begin(),ring.end());
for(int i=ring.size()-1;i>=0;i--){
if(q<=ring[i]){
printf("%d",ans+q-1);
return 0;
}
ans+=ring[i]-1;
q-=ring[i];
}
printf("%d",ans);
}
T4
有N个城市,被M条双向道路连接。 在保证图联通的情况下去掉尽可能多的边使得剩余边边权和最小。
问对于每一条边,可能被保留时边权最大为多少
\(N\le 10^5,N-1 \le M \le 10^6 ,0\le w_i\le 10^9\)
有N个城市,被M条双向道路连接。 每条双向道路都有一个维修费用。
国王想要去掉尽可能多的边,使得留下来的边依旧能使王国的任意两个城市之间都有经过一条或多条边的路径。在所有的方案中, 国王希望留下来的边的维修费用之和最小。
现在,国王准备调整一些边的维修费用来影响最后留下的边的结果。对于每条边,他希望你告诉他,在保证这条边有希望被留下来的同时,这条边的维修费用最大能是多少。
(或者可以说,在保证该边在最小生成树的前提下,边权最大为多少)
显然就是个最小生成树的题
对于树上边,我们要求他比环上最小非树边小
对于非树边,我们要求他比环上最大树边小
然后我们就转换成了求路径最大值和覆盖路径的问题
显然的,这题可以拿树剖切掉,太板了,但是我赛时写挂了
同时,这题可以拿倍增切掉,我们平常使用的是倍增表的合并,但是我们这题同时需要倍增表的拆分。
我们在ST表打lazytag,同时在结束时将大区间的lazytag下传到小区间
同时,可以拿dsu on tree做
我们可以搞一个差分。在u,v打一个insert标记,在lca打一个erase标记,合并时维护一个set,动态查询最小值
#include<bits/stdc++.h>
#define INF 1000000000
using namespace std;
const int N=1e5+50,M=2e6+50;
struct Edge{
int u,v,w,id;
bool operator<(const Edge &b){
return w<b.w;
}
}edge[M];
int head[N],nxt[M],to[M],id[M],W[M],num;
int father[N];
int fa[N][18],mx[N][18],lazytag[N][18];
int whichedge[N];
bool tag[M];
int dep[N],ans[M];
int n,m;
void add(int u,int v,int w,int idx){
++num;nxt[num]=head[u];to[num]=v;W[num]=w;id[num]=idx;head[u]=num;
}
int find(int x){
if(father[x]==x)return x;
return father[x]=find(father[x]);
}
void dfs(int u){
for(int i=1;i<=17;i++){
fa[u][i]=fa[fa[u][i-1]][i-1];
mx[u][i]=max(mx[fa[u][i-1]][i-1],mx[u][i-1]);
}
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==fa[u][0])continue;
fa[v][0]=u;
mx[v][0]=W[i];
dep[v]=dep[u]+1;
whichedge[v]=id[i];
dfs(v);
}
}
void init(){
for(int i=1;i<=n;i++)father[i]=i;
for(int i=1;i<=n;i++)
for(int j=0;j<=17;j++)
lazytag[i][j]=INF;
}
void modify(int u,int v,int w){
if(dep[u]>dep[v])swap(u,v);
for(int i=17;i>=0;i--)
if(dep[fa[v][i]]>=dep[u]){
lazytag[v][i]=min(lazytag[v][i],w);
v=fa[v][i];
}
if(u==v)return;
for(int i=17;i>=0;i--){
if(fa[u][i]!=fa[v][i]){
lazytag[u][i]=min(lazytag[u][i],w);
lazytag[v][i]=min(lazytag[v][i],w);
u=fa[u][i];v=fa[v][i];
}
}
lazytag[u][0]=min(lazytag[u][0],w);
lazytag[v][0]=min(lazytag[v][0],w);
}
int query(int u,int v){
int ans=0;
if(dep[u]>dep[v])swap(u,v);
for(int i=17;i>=0;i--)
if(dep[fa[v][i]]>=dep[u]){
ans=max(ans,mx[v][i]);
v=fa[v][i];
}
if(u==v)return ans;
for(int i=17;i>=0;i--){
if(fa[u][i]!=fa[v][i]){
ans=max(ans,mx[u][i]);
ans=max(ans,mx[v][i]);
u=fa[u][i];v=fa[v][i];
}
}
ans=max(ans,mx[u][0]);
ans=max(ans,mx[v][0]);
return ans;
}
int main(){
scanf("%d%d",&n,&m);init();
for(int i=1;i<=m;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
edge[i].u=u;edge[i].v=v;edge[i].w=w;edge[i].id=i;
}
sort(edge+1,edge+m+1);
for(int i=1;i<=m;i++){
int u=edge[i].u,v=edge[i].v,w=edge[i].w;
int fx=find(u),fy=find(v);
if(find(fx)!=find(fy)){
father[fx]=fy;
tag[i]=1;
add(u,v,w,edge[i].id);add(v,u,w,edge[i].id);
}
}
dep[1]=1;
dfs(1);memset(ans,-1,sizeof(ans));
for(int i=1;i<=m;i++){
if(!tag[i]){
ans[edge[i].id]=query(edge[i].u,edge[i].v);
modify(edge[i].u,edge[i].v,edge[i].w);
}
}
for(int i=17;i>=1;i--){
for(int j=1;j<=n;j++){
lazytag[j][i-1]=min(lazytag[j][i-1],lazytag[j][i]);
lazytag[fa[j][i-1]][i-1]=min(lazytag[fa[j][i-1]][i-1],lazytag[j][i]);
}
}
for(int i=1;i<=n;i++)
ans[whichedge[i]]=lazytag[i][0];
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号