针对燃油运输类车辆调度问题设计的蚁群算法模型

一、问题建模

1. 问题特征

• 多车辆协同：N辆油罐车从集货中心出发
• 多客户配送：M个客户点（加油站/储油库）
• 双目标优化： 最小化总运输成本（燃油消耗+车辆折旧） 最大化客户满意度（准时送达率）
• 核心约束： 车辆载重限制（≤20吨） 硬时间窗（客户要求送达时间） 油耗非线性模型（与载重、坡度相关）

2. 数学模型

目标函数：

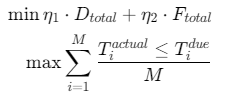
约束条件：

---

二、蚁群算法设计

1. 信息素结构

% 三维信息素矩阵：[路径][车辆][时间窗]
pheromone = rand(N_path, N_vehicle, T_max) * 0.1;

2. 启发式信息设计

多维度启发因子：

% 距离启发因子（距离倒数）
eta_distance = 1 ./ distance_matrix;

% 油耗启发因子（非线性模型）
eta_fuel = 1 ./ (a*distance + b*load + c*grade);

% 时间窗启发因子（剩余时间权重）
eta_time = 1 ./ (due_time - current_time);

3. 状态转移规则

概率计算：

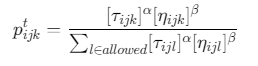
动态参数调整：

alpha = 1.2;    % 信息素重要度
beta = 3.5;     % 启发式重要度
rho = 0.15;     % 信息素挥发系数

4. 多目标协同机制

帕累托前沿更新：

% 非支配排序
[fronts, ~] = non_dominated_sort(costs, satisfactions);

% 拥挤度计算
crowding_distance = calculate_crowding(fronts);

% 外部档案更新
archive = update_archive(fronts, crowding_distance);

---

三、算法实现流程

1. 初始化阶段

% 参数设置
num_ants = 30;        % 蚂蚁数量
max_iter = 200;       % 最大迭代次数
Q = 100;              % 信息素增量常数

% 数据预处理
[distance_matrix, time_matrix, fuel_matrix] = preprocess_data();

% 初始信息素
pheromone = ones(N_path, N_vehicle);

2. 蚂蚁路径构建

for ant = 1:num_ants
    current_node = depot;
    unvisited = 1:M;
    path = [];
    
    while ~isempty(unvisited)
        % 计算转移概率
        probabilities = calculate_probabilities(current_node, unvisited);
        
        % 轮盘赌选择
        next_node = roulette_wheel_selection(probabilities);
        
        % 更新路径
        path = [path, next_node];
        unvisited(unvisited == next_node) = [];
        current_node = next_node;
    end
    
    % 返回仓库
    path = [path, depot];
    
    % 计算目标函数值
    [cost, satisfaction] = evaluate_solution(path);
    
    % 更新外部档案
    update_archive(path, cost, satisfaction);
end

3. 信息素更新

% 信息素挥发
pheromone = (1 - rho) * pheromone;

% 信息素增强
for i = 1:num_ants
    path = ants(i).path;
    delta_pheromone = Q / calculate_total_cost(path);
    
    for j = 1:length(path)-1
        pheromone(path(j), path(j+1)) = ...
            pheromone(path(j), path(j+1)) + delta_pheromone;
    end
end

---

四、MATLAB实现示例

1. 主程序框架

%% 参数设置
num_customers = 50;
num_vehicles = 8;
depot = [0,0];

%% 数据生成
[customers, demands, time_windows] = generate_data(num_customers);

%% 算法运行
aco = AntColonyOptimizer(num_ants, max_iter);
[best_path, costs, satisfactions] = aco.optimize(customers, demands, time_windows);

%% 结果可视化
plot_solution(best_path, depot);

2. 核心类定义

classdef AntColonyOptimizer
    properties
        num_ants
        max_iter
        alpha
        beta
        rho
        Q
    end
    
    methods
        function obj = AntColonyOptimizer(num_ants, max_iter)
            obj.num_ants = num_ants;
            obj.max_iter = max_iter;
            obj.alpha = 1.2;
            obj.beta = 3.5;
            obj.rho = 0.15;
            obj.Q = 100;
        end
        
        function [best_path, costs, satisfactions] = optimize(obj, customers, demands, time_windows)
            % 初始化信息素
            pheromone = ones(size(customers,1)+1);
            
            best_cost = inf;
            best_satisfaction = 0;
            
            for iter = 1:obj.max_iter
                % 蚂蚁路径构建
                paths = cell(obj.num_ants,1);
                costs = zeros(obj.num_ants,1);
                satisfactions = zeros(obj.num_ants,1);
                
                for ant = 1:obj.num_ants
                    path = construct_path(pheromone, customers, demands, time_windows);
                    [cost, satisfaction] = evaluate_solution(path);
                    
                    if cost < best_cost
                        best_cost = cost;
                        best_path = path;
                    end
                    
                    paths{ant} = path;
                    costs(ant) = cost;
                    satisfactions(ant) = satisfaction;
                end
                
                % 信息素更新
                pheromone = update_pheromone(pheromone, paths, costs);
            end
        end
    end
end

参考代码 根据蚁群算法，建立蚁群算法模型，适合燃油运输类，车辆调度类问题 www.youwenfan.com/contentcnk/78758.html

五、应用场景

1. 多能源车辆调度： 支持柴油/电动/混动车辆混合调度 考虑充电桩位置与充电时间
2. 危险品运输优化： 增加安全距离约束 事故风险路段规避
3. 动态需求响应： 处理客户临时增减货需求 基于强化学习的动态重调度