AC自动机学习笔记

AC自动机学习笔记

前置芝士：KMP Trie树

AC自动机就是KMP和Trie树的结合体，KMP用于单模式串的字符串匹配，AC自动机用于多模式串字符串匹配，比如说我们在一个文章中寻找一个单词可以用KMP，然后找多个单词的话，就得使用AC自动机来解决了。

实现AC自动机

具体思路

首先用模式串构造Trie树，我们这里放she,he,say,shr,her来当示例

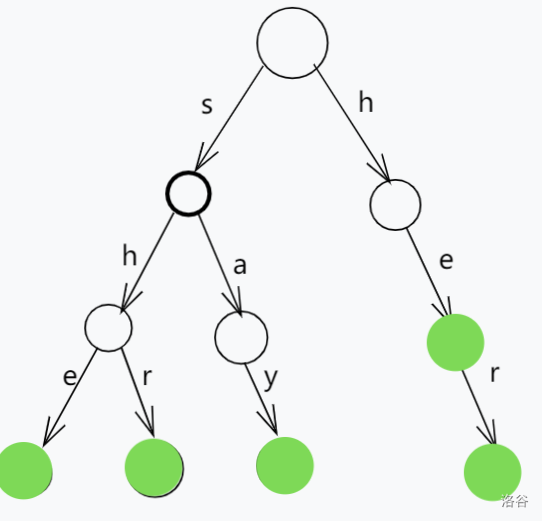
我们在kmp算法中还定义了一个失配指针 \(next\) 数组，这样的我们当失配的时候，就可以快速移动指针减少不必要的比较。

\(next_i\) 数组的意思是以 \(p_i\) 结尾的后缀，能够从1开始的前缀的最大坐标。在AC自动机里面也是这样表示的。

那么我们也可以在AC自动机里面也弄一个是失配指针 \(next\) 数组，然后在AC自动机里面如果我们需要求出来 第 \(i\) 层的 \(next\) 数组，就必须先求出来第 \(i-1\) 层(以及前面)的 \(next\) 数组。

然后由于每次向下更新 \(next\) 的值，那么就要使用 \(bfs\) ，我们看一下图中用的 \(next\) 指针的例子。

橙色的就表示 \(next\) 指针指向的地方。

kmp \(next\) 指针求法：

for(int i = 2, j = 0; i <= n; i ++ )
{
    while(j && q[i] != q[j + 1]) j = ne[j]; 
    if(q[i] == q[j + 1]) j ++ ; 
    ne[i] = j; 
} 

AC自动机 \(next\) 指针求法：

void build()
{
    int head = 0, tail = -1;
    for(int i = 0; i < 26; i ++ )
        if(trie[0][i]) q[ ++ tail] = tr[0][i];
 
    while(head <= tail)
    {
        int t = q[head ++ ];
        for(int i = 0; i < 26; i ++ )
        {
            int c = trie[t][i];
            if(!c) continue;

            int j = nxt[t];
            while(j && !trie[j][i]) 
                j = nxt[j];
            if(trie[j][i]) 
                j = trie[j][i];
            nxt[c] = j;
            q[ ++ tt] = c;
        }
    }
}

匹配过程通过类比KMP算法也很容易解决：

//有多少个模板串在文本串中出现过
for(int i = 0, j = 0; str[i]; i++)
{
    int t = str[i] - 'a';
    while(j && !trie[j][t]) j = nxt[j];
    if(trie[j][t]) j = trie[j][t];
    int p = j;
    while(p)
    {
        res += cnt[p];
        cnt[p] = 0;
        p = nex[p];
    }
}

这段代码匹配的是以 \(str_i\) 的最长后缀，我们假设文本串为 "qwher" ，模式串为 "he","whe"，如果当 \(str_i\) 为 \(e\) 的时候，我们所匹配的是 "whe" 这个模式串，然后又由于"he"是"whe"的后缀，"he" 也出现在文本串里面，所以我们要加上"whe"的"e"的失配指针 \(next\) 指针指向的点，但是这种情况的时间复杂度是 \(O(n^2)\) 的，所以我们考虑优化为trie图。

优化为trie图

消耗时间最多的语句是：

while(j && !trie[j][t]) j = nxt[j];

由于我们不断的往上跳 \(next\) 指针，就知道 \(j\) 的下一个字符是 \(t\)

那么我们的优化思路是这样的，更改 trie ，使得我们一次性就可以达到我们想要的位置

我们知道，在匹配的时候，如果当前匹配的字符是 \(t\) ，在 trie 树里的字符为 \(j\) ，如果我们 \(j\) 存在像 \(t\) 这样的子节点，就直接跳。 否则如果没有的话，我们就会不停往上跳，知道存在。

所以我们得到的策略就是，当 \(t\) 存在不存在 \(i\) 这样的子节点的时候，在trie图中指向 \(next_t\) 的 \(i\) 这个儿子，从而达到匹配过程中不存在这个儿子的时候直接跳到存在这个儿子的后缀去。

当存在这个儿子的时候仍然只需要将这个儿子的 \(next\) 值为 \(trie_{next_t,i}\)

代码如下：

void build()
{
    int head = 0, tail = -1;
    for(int i = 0; i < 26; i ++ )
        if(trie[0][i]) q[++ tail] = trie[0][i];
    while(head <= tail)
    {
        int t = q[head ++ ];
        for(int i = 0; i < 26; i ++ )
        {
            int p = trie[t][i];
            if(!p) trie[t][i] = trie[fail[t]][i];
            else
            {
                fail[p] = trie[fail[t]][i];
                q[ ++ tail ] = p;
            }
        }
    }
}

匹配过程也可以去掉 while 循环了。

for(int i = 0, j = 0; str[i]; i ++ )
{
    int t = str[i] - 'a';
    j = trie[j][t];
    int p = j;
    while(p)
    {
        res += cnt[p];
        if(cnt[p]) cnt[p] = 0;
        p = fail[p];
    }
}

https://blog.csdn.net/weixin_53360179/article/details/119718426