kmp匹配

题目传送门

kmp算法

首先我们得先知道朴素版本的字符串匹配的时间复杂度为\(O(nm)\),所以我们这时后就得使用复杂度为\(O(n+m)\)的kmp算法，我们先看一下算法流程。

我们假设蓝线之前的字符串是已经匹配成功了，但\(s_i\)和\(q_{j+1}\)却不相等了，那这时候我们就要让红线向后移动，那具体移动多少？这时侯就得运用到kmp算法中的\(next\)数组。

1.next数组的求法

首先就是定义，我们知道\(next\)它存储的是每一个下标对应的“部分匹配值”，那该怎么求呢？

我们来看以下

对\(next_j\) ，是\(p(1,j)\)串中前缀和后缀相同的最大长度（部分匹配值），即 \(p( 1, next[ j ]) = p( j - next_j + 1, j )\)

我们再来模拟一下\(next\)数组的求法。

设\(q = 'abcab'\)

q	a	b	c	a	b
下标	1	2	3	4	5
\(next\)	0	0	0	1	2

\(next_1\),前缀为空集，后缀也为空集，则值为\(0\)

\(next_2\)前缀为\(a\),后缀为\(b\),则值为\(0\)

\(next_3\)前缀为\({ a , ab }\)后缀 =$ { c , bc}$,则值为\(0\)

\(next_4\)前缀 = \({ a , ab , abc }\)后缀 = \({ a , ca , bca }\)值为 1;

\(next_5\)前缀 \({ a , ab , abc , abca }\)后缀 = \({ b , ab , cab , bcab}\)值为\(2\);

for(int i = 2, j = 0; i <= n; i ++ )
{
    while(j && q[i] != q[j + 1]) j = ne[j]; 
    if(q[i] == q[j + 1]) j ++ ; 
    ne[i] = j; 
} 

2.匹配字符串

回到开头那个场景，我们这时侯不匹配了，于是我们此时要移动\(q\)串（不是移动1格，而是直接移动到下次能匹配的位置,也就是移动\(next_j\))。

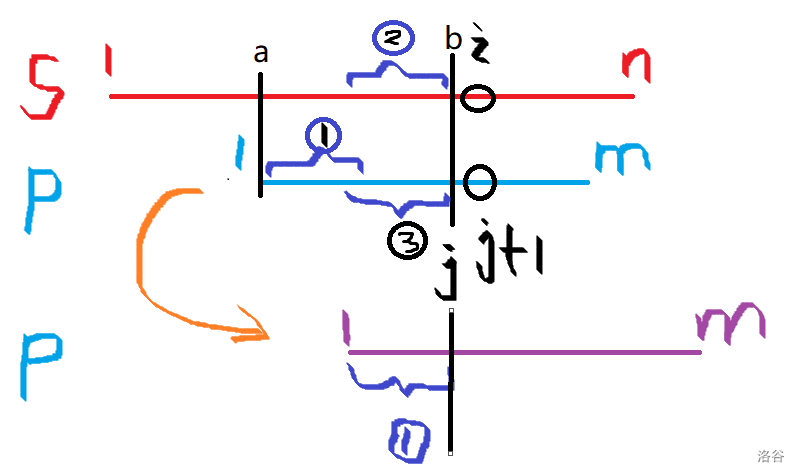
由匹配可知 1串等于3串，3串等于2串

for(int i = 1, j = 0; i <= m; i ++ )
{
    while(j && s[i] != p[j + 1]) j = ne[j];//不能匹配
    if(s[i] == p[j + 1]) j ++;
    if(j == n)
    {
        //匹配成功
        printf("%d ",i - j);
        j = ne[j];
    }
}

for语句第二行表示这时候后面的字符串匹配了，我们就可以将j的为前进一位。

#include<iostream>

using namespace std;

const int N=100010,M=1000010;

char q[N],s[M];

int ne[N];//保存next数组

int main()
{
    int n,m;

    cin >> n >> q + 1 >> m >> s + 1;

    for(int i = 2, j = 0; i <= n; i ++ )
    {
        while(j && q[i] != q[j + 1]) j = ne[j]; 
        if(q[i] == q[j + 1]) j ++ ; 
        ne[i] = j; 
    } 
    for(int i = 1, j = 0; i <= m; i ++ )
    {
        while(j && s[i] != q[j + 1]) j = ne[j]; 
        if(s[i] == q[j + 1]) j ++ ; 
        if(j == n) 
        {
            printf("%d ",i - j);
            j = ne[j];
        }
    }

    return 0;
}

完整代码。