左偏树

在这里先膜拜大神 cyx, 五年级就回了(在我旁边切紫题)。

对于一个小根堆, 我们考虑他们的合并, 我们可以通过一种每次和右儿子和另一个节点合并的方式, 用时间复杂度为 \(O(右儿子的深度)\)。这样, 我们就会有个想法, 只需要办证每次左儿子深度 > 右儿子深度, 这样就可以保证时间复杂度为 \(O(\log n)\) 合并。

例题

luogu P4331

首先根据题解我们知道, 我们每次维护后缀中位数即可

虽然这个东西感觉不符合直觉, 但是我们可以伪证一下。

首先先挂一个实现的证明 https://www.luogu.com.cn/discuss/602826。

我们考虑为什么合并两个区间是这两个区间的中位数。

首先, 我们考虑如果其中前面的那个东西保持不变。

我们令前一个的中位数为 \(x\), 后一个的中位数为 \(y\)。

我们考虑前一个位置如果还是保持 \(x\) 不变。

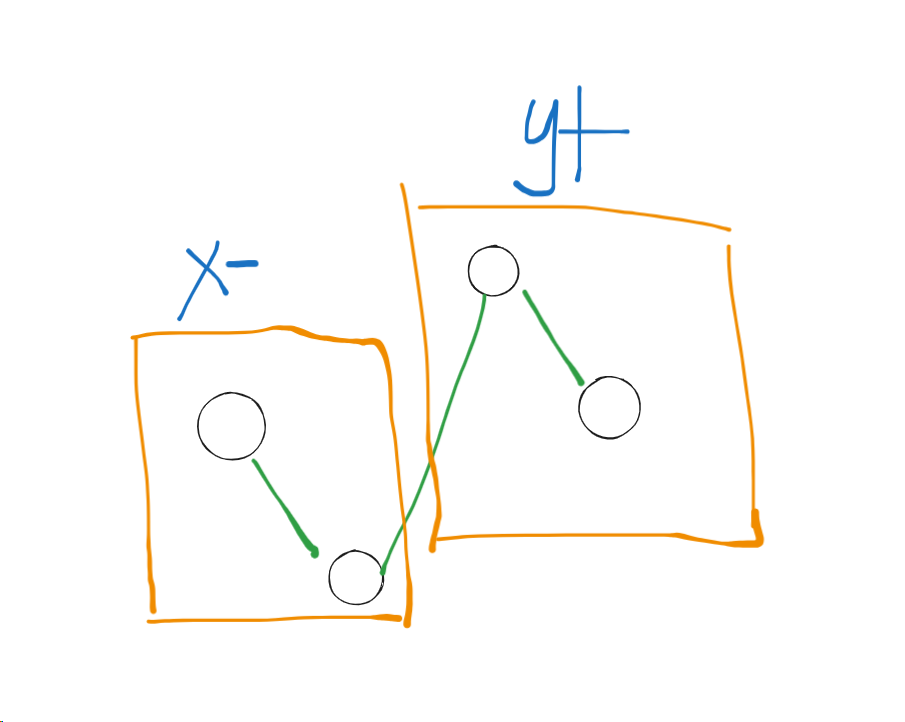
如果你左边的那一块选 \(y\), 右边的那一块选 \(y+\), 则原来一定中位数分布如图, 所以他们不会合并成一个块, 矛盾。

对于右边的快如果不变, 可以用类似的方法证明。

我们知道前一段最后的元素和后一段开始的元素介于[y, x]之间, 所以可以用类似的方法, 我们可以证明合并后前面一块取得值都相等, 后面一块选的值都相等, 且后一块为前一块, 即所有位置取值相等。

所以是取中位数最优。

code

#include<bits/stdc++.h>

using namespace std;

using LL = long long;

const int N = 5e6 + 5;

struct Node{
  int p1, p2, sz, l;
};

vector<Node>stk;
short digdig[N];
bool vis[N];
int n, a[N], b[N], rc[N], sz[N], lc[N], tot, wyt[N];
LL sum;

int Left_tree_updata(int x, int y){
  if(!x || !y)return x + y;
  if(vis[x] || vis[y]){
    return (vis[x] ? y : x);
  }
  if(b[x] > b[y]){
    rc[x] = Left_tree_updata(rc[x], y);
    sz[x] = sz[rc[x]] + sz[lc[x]] + 1;
    if(digdig[rc[x]] > digdig[lc[x]])swap(lc[x], rc[x]);
    digdig[x] = digdig[rc[x]] + 1;
    return x;
  }
  rc[y] = Left_tree_updata(rc[y], x);
  sz[y] = sz[rc[y]] + sz[lc[y]] + 1;
  if(digdig[rc[y]] > digdig[lc[y]])swap(lc[y], rc[y]);
  digdig[y] = digdig[rc[y]] + 1;
  return y;
}
int Erase(int x){
  if(vis[x]){
    return x;
  }
  int rt = Left_tree_updata(lc[x], rc[x]);
  lc[x] = rc[x] = digdig[x] = 0;
  sz[x] = 1;
  return rt;
}

void Join(int p, int &super, int flag){
  if(!p || vis[p])return ;
  Join(lc[p], super, flag);
  Join(rc[p], super, flag);
  b[p] *= flag;
  super = Left_tree_updata(super, p);
}

int main(){
  ios::sync_with_stdio(0), cin.tie(0);
  cin >> n;
  for(int i = 1; i <= n; ++i){
    cin >> a[i];
    a[i] -= i;
    b[tot + 1] = a[i];
    vis[tot + 2] = 1;
    sz[tot + 1] = 1, sz[tot + 2] = 0;
    stk.push_back({tot + 1, tot + 2, 1, i});
    tot += 2;
    for(; stk.size() >= 2 && b[stk.back().p1] < b[stk[stk.size() - 2].p1]; ){
      auto cct1 = stk.back();
      stk.pop_back();
      auto cct2 = stk.back();
      stk.pop_back();
      if(cct1.sz > cct2.sz)swap(cct1, cct2);
      cct2.p1 = Left_tree_updata(cct2.p1, cct1.p1);
      cct2.p2 = Left_tree_updata(cct2.p2, cct1.p2);
      cct2.sz += cct1.sz;
      cct2.l = min(cct2.l, cct1.l);
      for(; sz[cct2.p1] > (cct2.sz + 1) / 2; ){
        int x = cct2.p1;
        cct2.p1 = Erase(cct2.p1);
        b[x] *= -1;
        cct2.p2 = Left_tree_updata(cct2.p2, x);
      }
      for(; sz[cct2.p1] < (cct2.sz + 1) / 2; ){
        int x = Erase(cct2.p2);
        b[cct2.p2] *= -1;
        cct2.p1 = Left_tree_updata(cct2.p1, cct2.p2);
        cct2.p2 = x;
      }
      stk.push_back(cct2);
    }
  }
  reverse(stk.begin(), stk.end());
  int rr = n;
  for(auto [p1, p2, sz, l] : stk){
    int now = b[p1];
    for(int pk = l; pk <= rr; ++pk){
      wyt[pk] = now;
    }
    rr = l - 1;
  }
  for(int i = 1; i <= n; ++i){
    sum += abs(a[i] - wyt[i]);
  }
  cout << sum << '\n';
  for(int i = 1; i <= n; ++i){
    wyt[i] += i;
    cout << wyt[i] << '\n';
  }
  return 0;
}