wqs二分
wqs 二分一般是解决如 \(n\) 个物品需要选恰好 \(m\) 个这种形式的题。
我们以最小值为例。
我们记 \(X\) 为所有方案的集合, 对于每个方案 \(x \in X\), 记\(f(x)\) 表示在这种方案下的贡献, \(g(x)\) 表示在这种方案下你选了几个物品。
所以我们如果把每个方案看作为一个坐标为 \((g(x), f(x))\) 的点, 我们就是要求出对于每一个 \(x\), 在这跟直线上 \(y\) 坐标最小的是哪个点。
我们记 \(A(v)\) 表示在 \(x=v\)中, 可选的点的 \(y\) 坐标最小为 \(A(v)\)
即我们需要的档案为 \(A(m)\)
一下写法建立在所有的 \(1 \le i \le n\), \((i, A(i))\) 形成一个下凸包。
我们考虑求出一条斜率为 \(k\) 的一次函数, 满足这条线段排除那些重合的点后有且经过一个点 \((v, A(v))\) (注意, 不需要经过原点) 我们可以肯定, 一定存在一条斜率唯一的, 因为构成了一个下凸包, 只经过这个点的代价。
但是这条线段经过的点一个都不确定, 所以我们可以通过上下移动的方式, 把这条线段其中一个点移到原点处。
假设这个图只有最终的最优点, 可以通过二分找到经过我们需要点的斜率, 然后就可以算出来了。
当我们需要让每个 \(x\) 只在最小的 \(y\) 时判断, 所以我们可以通过取最小值的方式实现。(因为若你选了一个不是最小 \(y\) 坐标的点, 在这条直线上那个最小 \(y\) 坐标的点一定比这个点更优秀)
如果对于所有的 \(g(x), f(x)\), 保证 \(g(x)\) 和 \(f(x)\) 均为正数, 就可以在整数上二分。
二分的上下界应该定到 \(max(abs(A(i) - A(i - 1))\)。
考虑一些模型下可以证明函数是凸的。
以下凸壳为例
我们其实就是判断对于每一个 \(k\), 都有 \(A(k) - A(k - 1) \le A(k + 1) - A(k)\)
如果存在四边形不等式。
四边形不等式说的是对于任意的 \(a \le b le c le d\), \(cost(a, c) + cost(b, d) \le cost(a, d) + cost(b, c)\)
我们可以把\(A(k)\)看成一条从 \(1\) 到 \(n\) 经过 \(k\) 条边的最短路。
若存在两条路径分别为 \(A(k)\) 与 \(A(k + 2)\), 则必然会存在一条在 \(A(k + 2)\) 中的一条边, 完全被 \(A(k)\) 包含。(可以通过反证证明)。

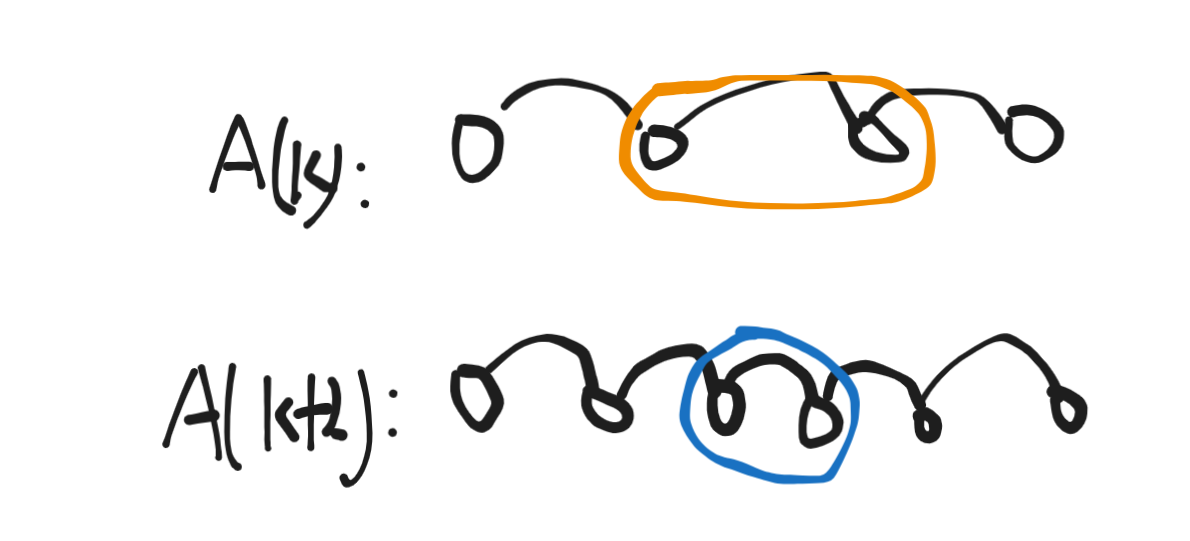
如图所示, 画黄圈的和画蓝圈的为上文所说的东西。
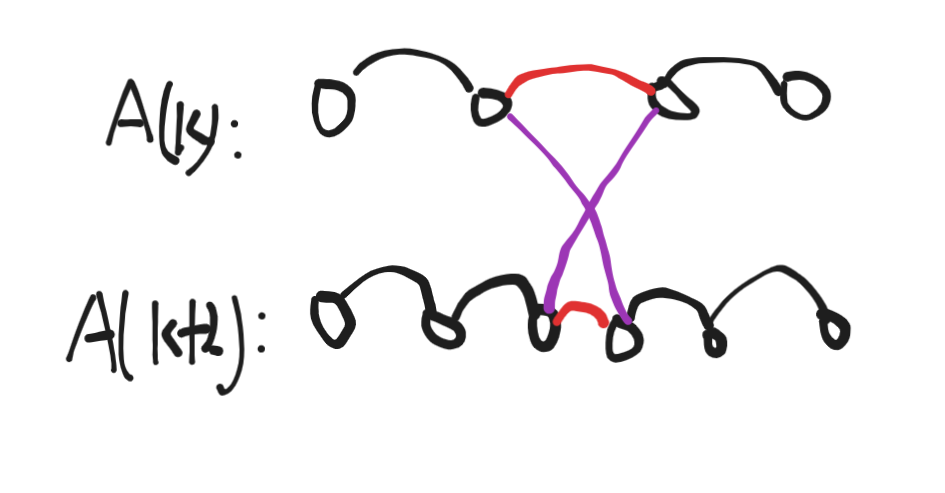
我们考虑如图所示的一条路径, 把红色的边断开, 紫色的边加入。
这样我们就有两条长度为 \(k + 1\) 的路径了
我们记从上面走到下面的经过紫色边的路径的权值和为 \(g0\), 从下到上的权值和为 \(g1\)
我们有 \(2A(k + 1) \le g0 + g1\), 由于四边形不等式, 所以 \(g0 + g1 \le A(k) + A(k + 2)\)
\(2A(k + 1) \le A(k) + A(k + 2)\)
\(A(k + 1) - A(k) \le A(k + 2) - A(k + 1)\)
如果需要跑网络流
网络流的定义天然满足这个限制。
例题
luogu P6246
由于这个满足四边形不等式, 所以我们这个 dp 是凸的。
我们考虑朴素的 dp
我们记二分的值为 \(mid\)
\(dp_i\) 表示考虑前 \(i\) 个且前 \(i\) 个数已完成皮配的最小贡献。
\(dp_i = mid + \min \limits_{j < i} \min \limits_{j < x \le i} \{a_x \cdot (x - j) - (sum_x - sum_j) + (sum_i - sum_x) + a_x \cdot (i - x) \}\)
我们可以把这个贡献拆成关于 \((x, i)\) 的贡献和关于 \((x, j)\) 的贡献, 然后你可以通过李超线段树创过去。
时间复杂度 \(O(n \log V \log n)\)
#include<bits/stdc++.h>
using namespace std;
using LL = long long;
const LL INF = 1e18;
const int N = 2e6 + 5;
int n, m, l, r, mid, a[N];
LL sum[N];
struct node{
int k;
LL b;
int id;
};
struct Ccf{
LL x;
int id;
}dp[N];
Ccf Min(Ccf a, Ccf b){
if(a.x != b.x){
return a.x < b.x ? a : b;
}
return a.id > b.id ? b : a;
}
struct C_Tree{
node tx[N * 4];
void build(int p, int l, int r){
tx[p] = {0, INF};
if(l == r)return ;
int mid = (l + r) >> 1;
build(p * 2, l, mid), build(p * 2 + 1, mid + 1, r);
}
void updata(int p, node x, int ql, int qr){
while(1){
int mid = (ql + qr) >> 1;
if(tx[p].k == 0 && tx[p].b == INF){
swap(tx[p], x);
return ;
}
if(1ll * mid * tx[p].k + tx[p].b > 1ll * mid * x.k + x.b){
swap(tx[p], x);
}
if(ql == qr)return ;
if(x.k <= tx[p].k){
ql = mid + 1;
p = p * 2 + 1;
}
else{
qr = mid;
p = p * 2;
}
}
}
Ccf getsum(int p, int l, int ql, int qr){
Ccf ans = {INF, 0};
while(1){
if(ql == qr){
return Min(ans, {1ll * tx[p].k * l + tx[p].b, tx[p].id});
}
int mid = (ql + qr) >> 1;
ans = Min(ans, {1ll * tx[p].k * l + tx[p].b, tx[p].id});
if(l <= mid){
qr = mid;
p *= 2;
}
else{
ql = mid + 1;
p = p * 2 + 1;
}
}
}
}T1, T2;
int Check(int x){
T1.build(1, 0, 2000000), T2.build(1, 1, n);
T1.updata(1, {0, 0, 0}, 0, 2000000);
for(int i = 1; i <= n; ++i){
auto now = T1.getsum(1, a[i], 0, 2000000);
now.x = now.x + 1ll * i * a[i] - sum[i];
T2.updata(1, {-a[i], now.x - sum[i] + 1ll * i * a[i], now.id}, 1, n);
auto [sp, uq] = T2.getsum(1, i, 1, n);
dp[i] = {sp + sum[i] - x, uq + 1};
T1.updata(1, {-i, sum[i] + dp[i].x, dp[i].id}, 0, 2000000);
}
return dp[n].id;
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; ++i){
cin >> a[i];
}
sort(a + 1, a + n + 1);
for(int i = 1; i <= n; ++i){
sum[i] = sum[i - 1] + a[i];
}
l = -1e9, r = 1e9;
while(l < r){
mid = (l + r + 1);
if(mid >= 0)mid /= 2;
else mid = (mid - 1) / 2;
int x = Check(mid);
if(x <= m)l = mid;
else r = mid - 1;
}
int x = Check(l);
cout << dp[n].x + m * l;
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号