后缀数组

后缀数组本质上是一个倍增, 每次求解 \(rk_{i, j}\) 表对于所有的 \(j\) 取 \([j ~ j + 2^i - 1]\), 这些字符按字典序排名为多少。

我们按字典序的想法, 先比那就前半段, 再比较后半段。

由于我们取得区间是一段后缀, 所以不可能出现一下这种情况。

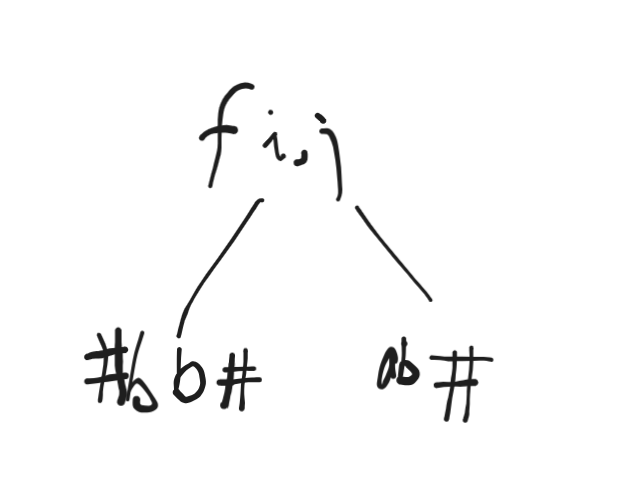
假设 '#' 代表空字符。

如果左边的串你最左侧为空, 你是无法比较他的大小的。

我们定义每个后缀为 \(suf_i\), \(sa_{rk_{+\infty}{i}} = i\), 定义 \(h_i = lcp(suf_{sa_i}, suf_{sa_{i + 1}})\)。

\(lcp(s, t)\) 表示 \(s\) 和 \(t\) 的最长公共前缀。Why?

则在排名上第 \(i\) 个字符到第 \(j\) 个字符的 \(lcp\) 为 \(\min \limits_{k = i}^{j - 1} h_{k}\)

Why?

我们假设他们的最长公共前缀为 \(x\), 则对于 \(i ~ (j - 1)\) 的每个 \(k\), 必然有 \(h_k \ge x\)。

若对于所有的 \(k \in [i, j - 1]\), 如都满足 \(h_k > x\), 则, 对于 \(x + 1\) 位, 他们一定相等, 所以 \(x \le x + 1\), 矛盾。

怎么求 \(h_i\), 我们考虑从原数组从小往大处理, 考虑一个位置 \(i\), 若 \(h_{rk[i - 1]} \ge 2\), 则 \(suf_{sa_{rk[i - 1] + 1}}, suf_{i - 1}\) 在 \([2 ~ h_i]\) 位一定相等, 又因为 \(suf_{sa_{rk[i - 1] + 1}}\) 取出第一个元素一定存在且在 \(i\) 的后面, 因为刚刚所说的性质, 得 \(h_{rk_i} \ge h_{rk_{i - 1}} - 1\)

可以从大到小维护一下。