2-SAT

调不出来题 www

定义

什么是 SAT, 我们有一些方程, 每个方程形如 \(x_i \and x_j \or x_k \xor x_z = 0/1\), \(x\) 均为 \(0/1\) 的 bool 数组我们需要求出一个解, 或者判断无解。

而 k-SAT, 就是所以分成的位置数数量最多为 \(k\) 的方程。

既然我们会定义了, 那我们考虑这个问题。

我们可以把一个点拆成两个点, 分别为 \((x_i == 0)\) 与 \((x_i == 1)\), 这样, 我们就可以把一个问题拆成形如 \(u \to v\) 表示如果 \(u\) 命题成立, \(v\) 就成立。我们在把他的逆反命题也建出来。显然, 这个关系具有传递性。

这样, 对于一个未知数 \(x_i\), 若 \((x_i == 0) \to (x_i == 1), (x_i == 1) \to (x_i == 0)\) 显然无解。

否则, 若 \((x_i == 0) \to (x_i == 1)\), 则必须 \(x_i = 1\), 若 \((x_i == 1) \to (x_i == 0)\) 则必须 \(x_i = 0\)

对于其他的点, 如果没有限制, 你可以随便选。

以上证明了他的必要性, 接下来证明充分性, 即如果选了位置 \((x_i == 0)\), 不会使一个 \(j\) 出现 \((x_j == 0)\) 和 \((x_j == 1)\) 同时选。

首先, 这个图会把原图分成一个正着的图和一个倒着的图。

我们假设选了 \((x_i == 0)\) 时存在 \(j\), 使得 \((x_j == 0)\) 与 \((x_j == 1)\) 一起选, 由于这个图具有刚刚说的性质, 所以 \((x_i == 0) \to (x_j == 0)\) 的对称路径为 \((x_j == 1) \to (x_i == 1)\), \((x_i == 0) \to (x_j == 1)\) 的对称路径为 \((x_j == 0) \to (x_i == 1)\)

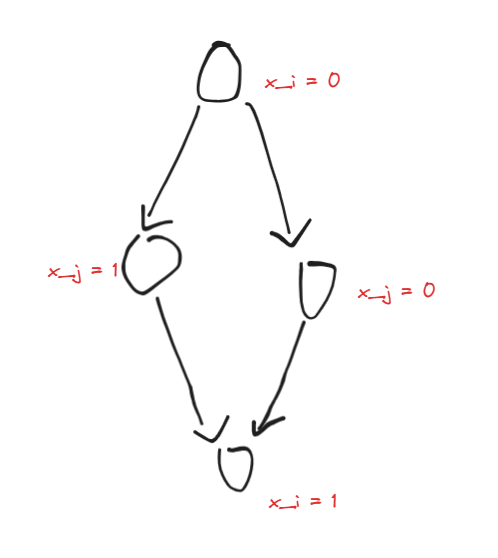
如图会发现 \((x_i == 0) \to (x_i == 1)\), 与假设矛盾, 所以这个算法是对的。

应用 1

求出字典序最大值。

对于每个位置, 如果他不能经过没有定颜色的边到达他的返点, 就可以选这个数字。