网络流

先把一些不会证的结论放着。
最大流
什么是最大流 ? 有一个图, 其中有一个源点和一个汇点, 每一条边有一定的流度最大值, 每个点有一个无线大的水桶, 源点有一个无线水的水井, 问每一条边只会经过一次水流时汇点能获得的最大水流量。
令源点为 \(s\), 汇点为 \(t\), 点数为 \(n\), 边数为 \(m\)。
对于每一条从 \(s \to t\) 路径, 我们令最小值为 \(x\), 则每一条边权值都减 \(x\), 然后建一条权值一样反向边。
为什么要建反向边 ?
我们令这条边为 \(u \to v\), 则 可能有两条路径不经过 \(u \to v\) 且 经过 \(u, v\) 的路径, 不过有可能经过了这一条边, 这一条边就相当于不选原来的边。
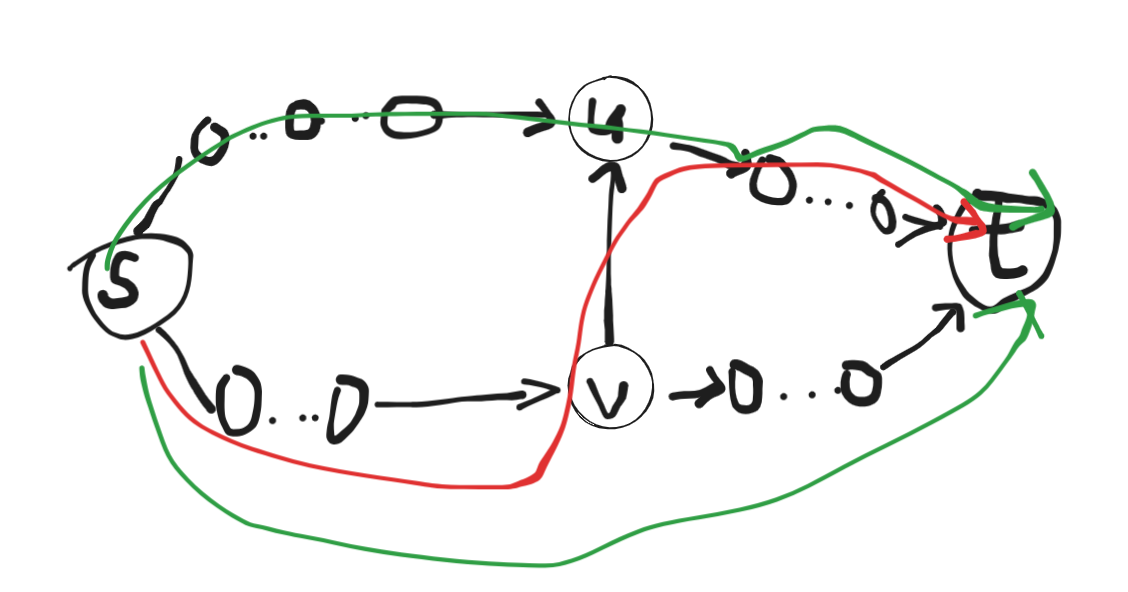
如图, 我们可能会搜到红色的路径, 而更优的是绿色的路径。
Dinic
我们可以每次找一条最短的增广路径, 按照增广路径解决, 对于一个点, 先把当前的流度出来好, 如能 dfs 就先 dfs, 不急着回溯。
我们不考虑单次 dfs 的时间复杂度, 而是考虑有多少条增广路径。
每次增广, 至少会让一条边消失, 所以最多只有 \(m\) 条增广, 每条增广路径做多 \(n\) 个点, 所以每次 bfs 后跑一遍的时间复杂的最多为 \(O(nm)\), 所以时间复杂度 \(O(n^2m)\)
模板 luoguP3376
#include<bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 1e4 + 5;
struct Edge{
int v, w, nxt;
}e[N];
int dep[N], n, m, s, t, u, v, w, head[N], tot, p[N];
long long ans, now;
queue<int>q;
void add(int u, int v, int w){
e[tot] = {v, w, head[u]};
head[u] = tot++;
}
LL dfs(int x, LL minx){
LL s = 0;
if(x == t)return minx;
for(; ~p[x]; p[x] = e[p[x]].nxt){
int v = e[p[x]].v, w = e[p[x]].w, id = p[x];
if(!w || dep[v] != dep[x] + 1)continue;
LL qp = dfs(v, min(minx, 1ll * w));
s += qp;
minx -= qp;
e[id ^ 1].w += qp;
e[id].w -= qp;
}
return s;
}
bool bfs(){
for(int i = 1; i <= n; ++i){
dep[i] = 0;
p[i] = head[i];
}
dep[s] = 1;
q.push(s);
while(q.size()){
auto u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].nxt){
int v = e[i].v, w = e[i].w;
if(!w || dep[v])continue;
dep[v] = dep[u] + 1;
q.push(v);
}
}
return dep[t];
}
int main(){
cin >> n >> m >> s >> t;
for(int i = 1; i <= n; ++i){
head[i] = -1;
}
for(int i = 1; i <= m; ++i){
cin >> u >> v >> w;
add(u, v, w);
add(v, u, 0);
}
while(bfs()){
ans += dfs(s, 1e18);
}
cout << ans;
return 0;
}
最小割
什么是割, 对于一个子图 \(G(V, E)\), 若两个集合 \(S, T, S \cup T = \varnothing\), \(s \cap T = V\), 这个割的代价为 \(\sum \limits_{u, v \in E, u \in S, v \in T} r(u, v)\) (其中, r(u, v)) 表示这条割的容量。
最小割就是代价最小的割。
我们可以把这个看成删到其中的一些边, 使得 \(s, t\) 不连通。
我们可以把这个看成一个更理想的情况, 就是每次可以让一条边的流量减少 \(1\), 使得 \(s\) 无法到达 \(t\)。这样, 我们就知道 最小割 \(\ge\) 最大流。我们考虑构造, 对于每一条增广路径, 把第一条满流量的边断开。这样我们就可以构造一个最小割。
为什么 ?
我们的问题在于会不会出现一种情况一个点他原本流行另一个点, 但是由于把这条边断开了, 所以他的流量会去其他的点, 使得可以到达 \(t\)。
对于在割掉的边后面的边, 显然不用考虑。
假设存在一个点 \(u\), 使得流向他的边没有满流, 假设我们存在一个点, 使得完里面注入流量还能继续到达 \(t\), 则一定是因为没有流量了(否则这是一条新的增广路径) (即来到这个点的边与假设矛盾都满了, 可以搁到流量到来的地方)。
最小割模型
我们已经学会了如何求最小割, 然我们看一些很经典的建边方法。
最大权闭合子图
我们可以解决一下问题, 有一些点, 他们有依赖关系, 形如选某些点后一定要选他的后继。每个点有一个权值, 可正可负, 对于依赖关系, 我们直接建一些边, 我们先把正权全部加起来, 然后让源点连续这些点, 边权为这个的正权, 每个负权的点连向汇点, 边权为他的绝对值。然后跑最小割。这样为什么是对的?由于存在关系的我们都连了边所以如果选等价于把右边的边断开, 不选等价于把左边的断开。
切糕模型

对于每个点, 我们把他分成值域个点, 我们考虑对于每个点, 如果选左边表示这个数至少大于某个值, 右边表示小于某个值, 我们可以把代价放在每条相邻的边上, 每次若割掉相当于选。
如何防止出现选左右边交替?
对于每个点, 我们连一条正无穷的反边即可。
对于每种限制, 我们可以拆成。
\(\exists c\), 若 \(x_v \le c\), 则 \(x_u \le w + c\), 这样, 我们就可以看成一个这两个点必须在同一个割的集合中, 只需要连一条正无穷的边即可。
关于网络流流量只有0/1的一些性质
如果存在一条方向变且连接两端点的变除了这条只有1条, 则如果到达一个点, 他能走的点唯一确定, 不可能离开.
例题(关于最小割的题) luogu P1646
为什么要写呢, 因为我发现了一些问题(感觉只有我会放)
由于我但是太sb了, 写了个神奇的写法, 但是发现0分, 看了下题解才改了。
具体怎么写 ?
对于每个点, 建两个点 \(wa_{i, j}\) 与 \(wb_{i, j}\), 建 \(S \to wa_{i, j}\), \(wb_{i, j} \to T\), \(wa_{i, j} \to wb_{i, j}\), 对于每个附加项, 连 \(S \to new_node\), \(new_node \to x, new_code \to y\) (x, y) 表示两个合法的反面。
这时你会发现一组 hack
1 2
1 1
100 110
1211
1000
建出来的图长这样
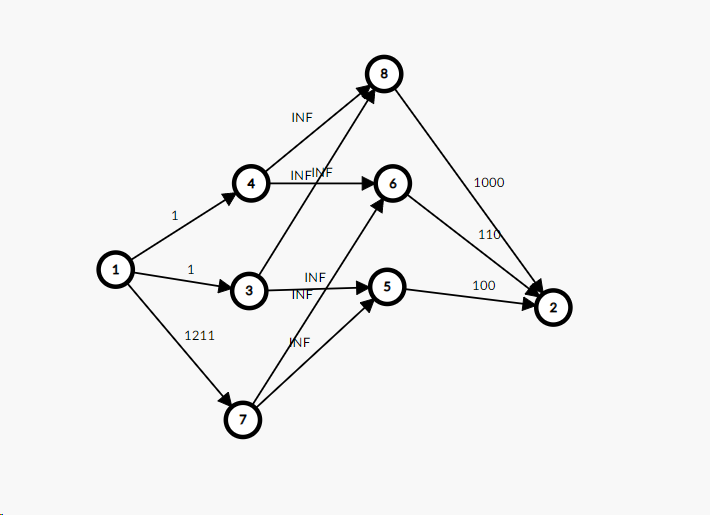
其中, \(1\) 为源点, \(2\) 为汇点, \(7, 8\) 为附加贡献的点。
错误的原因在于, 你其实可以把每个位置分出的连接源点和汇点的边全断掉, 即你可能存在同时获得选文的附加值和选理的附加值。
所以经过修改, 可以获得一下代码。
#include<bits/stdc++.h>
using namespace std;
const int N = 8e4 + 5, M = 105, INF = 1e9;
int head[N], tot, dist[N], p[N], s, t, n, cct, m, ida[M][M], idb[M][M], x;
long long ans;
queue<int>q;
struct Edge{
int v, w, nxt;
}e[20 * N];
void add(int u, int v, int w){
e[tot] = {v, w, head[u]};
head[u] = tot++;
}
int dfs(int x, int minx){
if(x == t)return minx;
int sum = 0;
for(; ~p[x]; p[x] = e[p[x]].nxt){
int i = p[x];
int v = e[i].v, w = e[i].w;
if(!w || dist[v] != dist[x] + 1)continue;
int now = dfs(v, min(minx, w));
minx -= now;
sum += now;
e[i].w -= now, e[i ^ 1].w += now;
if(!minx)break;
}
return sum;
}
bool bfs(){
for(int i = 1; i <= cct; ++i){
p[i] = head[i];
dist[i] = 0;
}
q.push(s);
dist[s] = 1;
while(q.size()){
auto u = q.front();
q.pop();
for(int i = head[u]; ~i; i = e[i].nxt){
int w = e[i].w, v = e[i].v;
if(!w || dist[v])continue;
dist[v] = dist[u] + 1;
q.push(v);
}
}
return dist[t];
}
int main(){
cin >> n >> m;
s = ++cct, t = ++cct;
for(int i = 1; i <= 8 * n * m; i++)head[i] = -1;
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; j++){
ida[i][j] = ++cct;
cin >> x;
add(s, cct, x);
add(cct, s, 0);
ans += x;
}
}
for(int i = 1; i <= n; ++i){
for(int j = 1; j <= m; ++j){
idb[i][j] = ida[i][j];
cin >> x;
add(ida[i][j], t, x);
add(t, ida[i][j], 0);
ans += x;
}
}
for(int i = 1; i < n; ++i){
for(int j = 1; j <= m; ++j){
cin >> x;
++cct;
add(s, cct, x);
add(cct, s, 0);
add(cct, idb[i][j], INF);
add(idb[i][j], cct, 0);
add(cct, idb[i + 1][j], INF);
add(idb[i + 1][j], cct, 0);
ans += x;
}
}
for(int i = 1; i < n; ++i){
for(int j = 1; j <= m; ++j){
cin >> x;
++cct;
add(cct, t, x);
add(t, cct, 0);
add(ida[i][j], cct, INF);
add(cct, ida[i][j], 0);
add(ida[i + 1][j], cct, INF);
add(cct, ida[i + 1][j], 0);
ans += x;
}
}
for(int i = 1; i <= n; ++i){
for(int j = 1; j < m; ++j){
cin >> x;
++cct;
add(s, cct, x);
add(cct, s, 0);
add(cct, idb[i][j], INF);
add(idb[i][j], cct, 0);
add(cct, idb[i][j + 1], INF);
add(idb[i][j + 1], cct, 0);
ans += x;
}
}
for(int i = 1; i <= n; ++i){
for(int j = 1; j < m; ++j){
cin >> x;
++cct;
add(cct, t, x);
add(t, cct, 0);
add(ida[i][j], cct, INF);
add(cct, ida[i][j], 0);
add(ida[i][j + 1], cct, INF);
add(cct, ida[i][j + 1], 0);
ans += x;
}
}
while(bfs())ans -= dfs(s, 1000000000);
cout << ans;
return 0;
}
所以提醒我们应该检查是不是会有矛盾的选择




 浙公网安备 33010602011771号
浙公网安备 33010602011771号