树状数组

树状数组

背景

• 由于 \(OIer\) 们对于数据更高效的储存、修改和查询的需要，一种数据结构树状数组营运而生。

介绍

• 树状数组是一个查询和修改时间复杂度都为 \(O(log(n))\) 的数据结构，主要用于：数组的单点修改和区间查询

在使用前缀和求区间和的算法中：

如果可以做到在 \(O(1)\) 的时间复杂度内查询任意的区间和，但是如果要修改其中一个点的值，那么需要修改一遍前缀和数组，修改的时间复杂度是 \(O(n)\) 。

这是极不平衡的。

树状数组便克服了这个弊端。

• 树状数组将整个数组分段处理，相对平衡了时间复杂度。

树状数组的实现

拆分原理

• 正如所有的整数都可以表示成 \(2\) 的幂和，我们也可以把一串序列表示成一系列子序列的和。采用这个想法，我们可将一个前缀和划分成多个子序列的和，而划分的方法与数的 \(2\) 的幂和具有极其相似的方式。
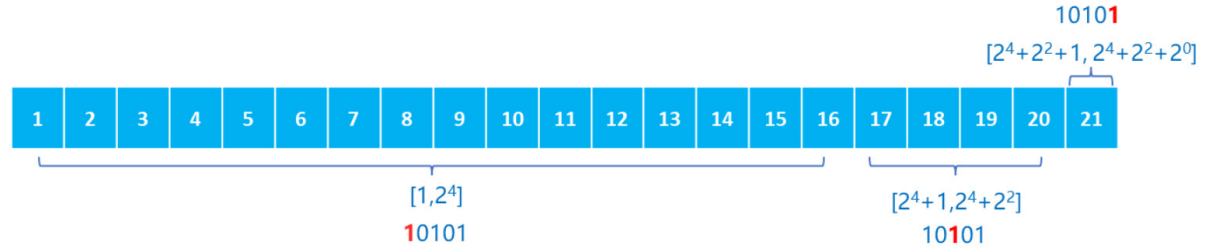
• 比如:整数 \(21\) 的对应的 \(2\) 进制是 \(10101\) ，对应计算\(=2^4+2^2+2^1\) ，因此一个长度为 \(21\) 的数组，可以拆分为三段：

• 子序列的个数是其二进制表示中 \(1\) 的个数。

• 据此，一个长度为 \(n\) 的区间 \([1,n]\) ，可以采用上述思想划分为 \(log(n)\) 个区间。

• 从右向左看，每个区间的大小其实是 \(n\) 对应二进制的最后一个 \(1\) 的 \(2\) 次幂。

求对应二进制的最后一个1的方法

• 定义一个函数 \(lowbit(x)\) ：代表 \(x\) 对应二进制从最后一位开始向后构成的值。

  e.g:

  \(lowbit(10)\) 返回 \(10\)

  \(lowbit(40)\) 返回 \(1000\)

• 计算方法：

  假设 \(x=270\) 对应的二进制为： \(1011,1000\) 。

  先将 \(x\) 取反 \(=0100,0111\) ，再 \(+1=0100,1000\) ，此时发现这个值和原来的 \(x\) 对应的二进制，最后一个 \(1\) 向后的值一致，前面的值正好相反，只要拿这两个值做 \(\&\) （按位与）运算，结果就是 \(lowbit(x)\) 的值。

  因此：\(lowbit(x)=x\&(~x+1)=x\&-x\)

划分方法

• 以 \(a[x]\) 结尾的区间，区间长度为 \(x\) 的最后一个 \(1\) 所对应的 \(2\) 的次幂。

1. 以 \(a[x]\) 结尾的区间，区间长度为 \(x\) 的最后一个 \(1\) 对应的 \(2\) 的次幂。

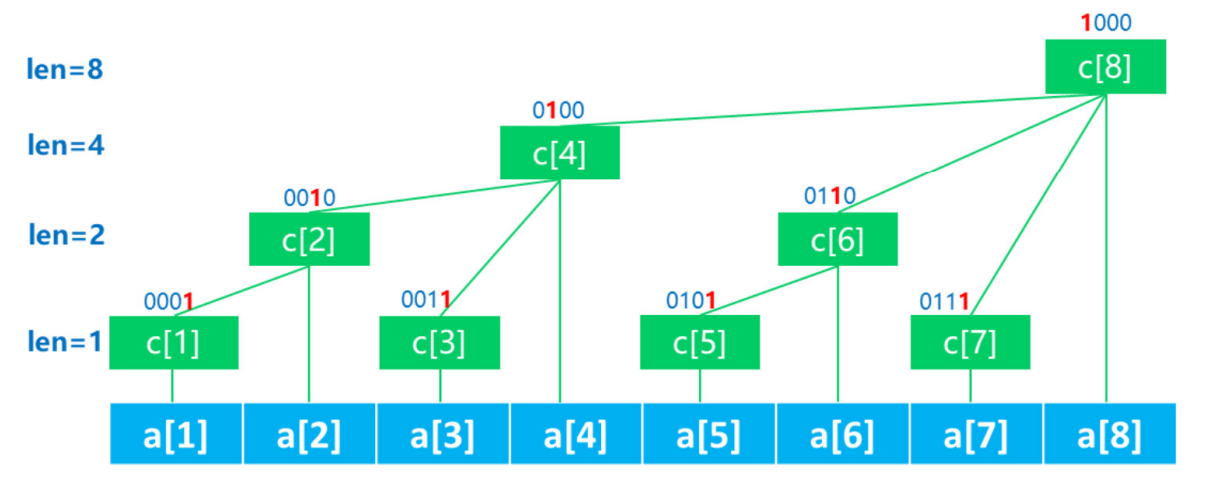
2. 设定 \(c[x]\) 表示： \(a\) 数组中，长度为 \(lowbit(x)\) 的区间和，所管理的区间为 \([x-lowbit(x)+1],x\) 。

3. 该结构的特点：

   a) 除树根外，结点 \(x\) 的父结点 \(=x+lowbit(x)\)

   b) 长度为 \(n\) 的数组 \(a\) ，所构建的树的深度 \(=log(n)\)

   注意：树状数组的下标一般从 \(1\) 开始，因为如果从 \(0\) 开始， \(lowbit(0)=0\) ，容易出现死循环。

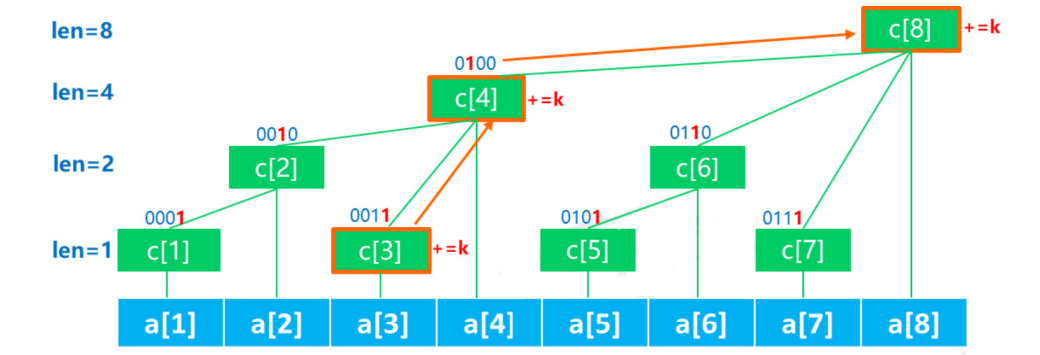
修改元素

//在数组a的第x个数上增加k的值
void add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i)){
        c[x]+=k;
    }
}

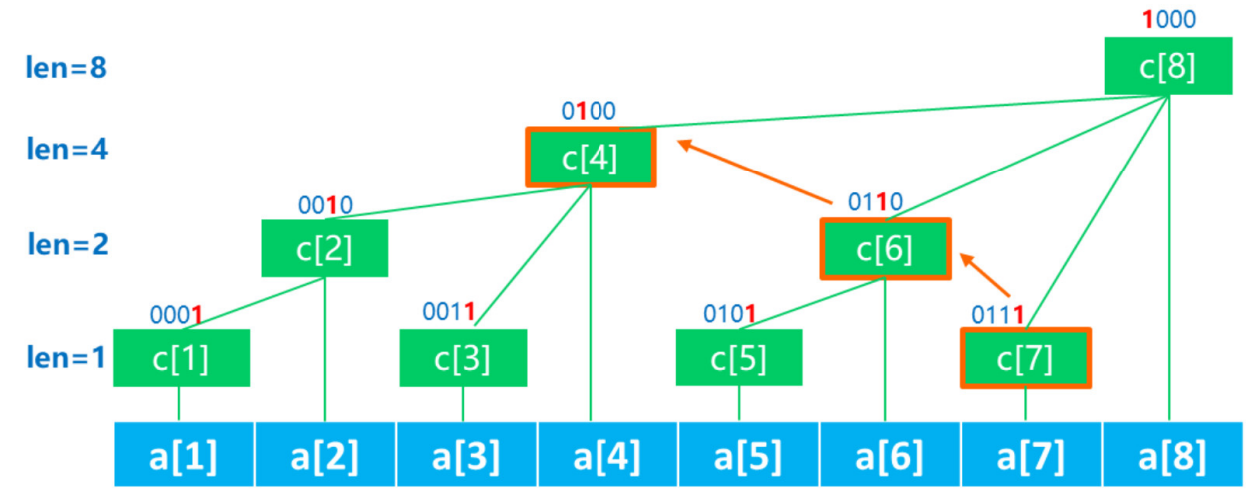
求前缀和

//查询数组下标[1,x]中的数的和
int qu(int x){
	int res=0;
    for(int i=x;i>0;i-=lowbit(i)){
		res+=c[i];
    }
    return res;
}

模板

#include<algorithm>
#include<iostream>
#include<string.h>
#include<stdio.h>
#include<string>
#include<vector>
#include<math.h>
#include<stack>
#include<queue>
#include<set>
#include<map>
using namespace std;
const int N=1e5+10;
int n;		//数的个数 
int c[N];	//前缀和 
int lowbit(int x){
	return x&-x;
}
void add(int x,int y){	//在x的位置加上y 
	for(int i=x;i<=n;i=i+lowbit(i)){
		c[i]+=y;
	}
	return;
}
int qu(int x){	//查询[1,x]的数的和 
	int res=0;
	for(int i=x;i>0;i=i-lowbit(i)){
		res+=c[i];
	}
	return res;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		int x;
		scanf("%d",&x);
		add(i,x);
	}
	int m;
	scanf("%d",&m);
	for(int i=1;i<=m;i++){
		int l,r;
		scanf("%d%d",&l,&r);
		printf("%d\n",qu(r)-qu(l-1));
	}
	return 0;
}