树状数组专题

树状数组

一、树状数组介绍

树状数组（也称为二叉索引树）是一种数据结构，它可以快速计算前缀和并支持 动态维护。与普通的前缀和数组相比，树状数组的优势在于它能够在$O(logn)$的时间复杂度内 更新单个元素的值，同时仍然能够在$O(logn)$的时间复杂度内 计算前缀和。这使得树状数组在 处理动态数据 时非常高效,以下是树状数组的常见使用场景及相关的简单例子：

单点更新与查询
树状数组支持在指定位置 更新元素，并且很快地查询更新后的结果。
- 例子：使用树状数组来计算数组$nums = [0, 0, 0, 0, 0]$中某个位置$i$之前的所有元素和。首先执行单点更新操作$update(2, 5)$，将位置$2$的元素更新为$5$。然后执行查询操作$query(4)$，即查询位置$4$之前的元素和，结果为 $0 + 0 + 5 + 0 = 5$。
区间更新与查询
树状数组借助 差分思想 还可以 支持对指定区间内的元素进行更新，并且快速查询更新后的结果。
- 例子：使用树状数组来计算数组$nums = [0, 0, 0, 0, 0]$中某个区间$[l, r]$内的所有元素和。首先执行区间更新操作$rangeUpdate(2, 4, 2)$，即将位置$2$到位置$4$的元素都加$2$。
数组逆序对统计
树状数组也可以用于高效地计算数组中的逆序对个数。
- 例子：给定数组$nums = [5, 2, 6, 1, 3, 4]$，使用树状数组来统计逆序对的数量。逆序对是指数组中的一对元素$(i, j)$，其中 $i < j$ 且 $nums[i] > nums[j]$。经过计算得到逆序对的数量为 $4$。
维护最大、最小值
树状数组维护最大值的思路与维护前缀和类似。我们可以建立一个树状数组，其中每个节点存储它所代表的区间的最大值。在更新元素时，我们需要 沿着树状数组的路径向上更新 所有受影响的节点，以保证它们存储的最大值始终正确。在查询区间最大值时，我们可以将查询区间分解为若干个小区间，然后 查询这些小区间 在树状数组中对应节点的 最大值，最后 取所有查询结果的最大值 作为最终结果。

树状数组维护区间最值

二、与普通前缀和区别

树状数组: 较快的修改时间$O(log_2N)$+较快的查询时间$O(log_2N)$
普通前缀和：较慢的修改时间$O(N)$+极快的查询时间$O(1)$

三、前置知识

$lowbit()$运算：非负整数$x$在二进制表示下最低位$1$及其后面的$0$构成的数值

举个栗子：
$lowbit(12)=lowbit([1100]_2)=[100]_2=4$

$Code$

int lowbit(int x){
    return x & -x;
}

四、树状数组结构

树状数组的本质思想是使用 树结构 维护 前缀和 ，从而把时间复杂度降为$O(log_2n)$。

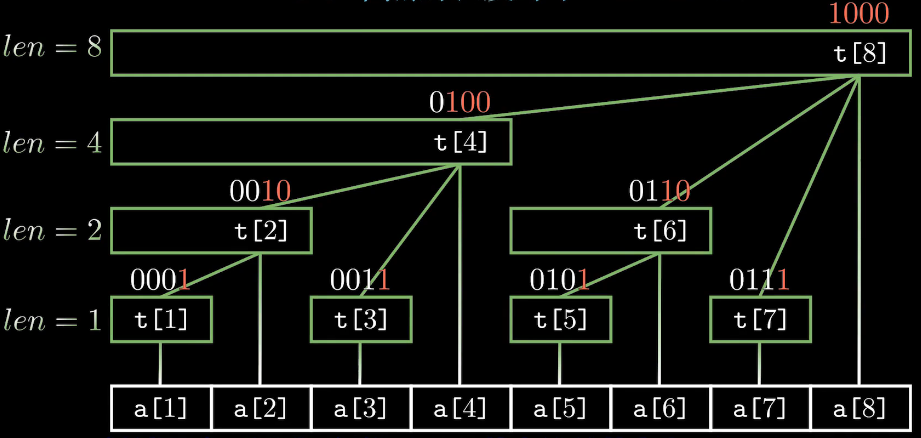
① 每个节点t[x]保存以x为根的子树中叶节点值的和
② 每个节点覆盖的长度为lowbit(x)
③ t[x]节点的父节点为t[x + lowbit(x)]
④ 树的深度为$log_2n+1$

五、树状数组操作

add(x, k)表示将序列中第x个数加上k。

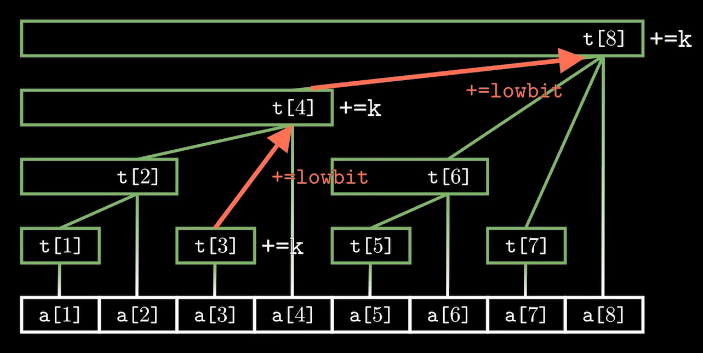
以add(3, 5)为例：
在整棵树上维护这个值，需要一层一层向上找到父节点，并将这些节点上的t[x]值都加上k，这样保证计算区间和时的结果正确。时间复杂度为$O(log_2n)$。

void add(int x, int k){
    for(int i = x; i <= n; i += lowbit(i)) t[i] += k;
}

ask(x)表示将查询序列前x个数的和

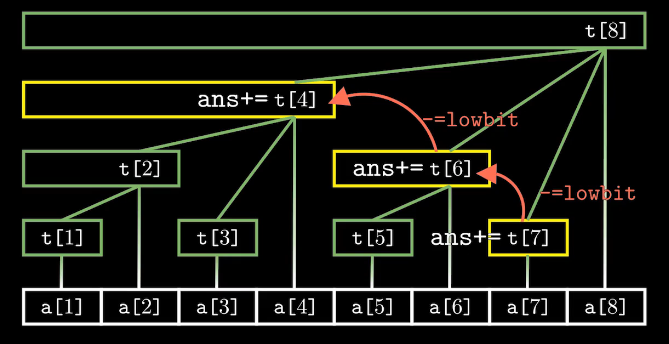
以ask(7)为例：
查询这个点的前缀和，需要从这个点向左上找到上一个节点，将加上其节点的值。向左上找到上一个节点，只需要将下标 x -= lowbit(x)，例如 7 - lowbit(7) = 6,6-lowbit(6)=4,4-lowbit(4)=0。

lowbit(7)=1 0111 ->截取最后一个数字1,是1
lowbit(6)=2 0110 ->截取最后一个数字1,是2
lowbit(5)=1 0101 ->截取最后一个数字1,是1
lowbit(4)=4 0100 ->截取最后一个数字1,是4
lowbit(3)=1 0011 ->截取最后一个数字1,是1
lowbit(2)=2 0010 ->截取最后一个数字1,是2
lowbit(1)=1 0001 ->截取最后一个数字1,是1

int ask(int x){
    int sum = 0;
    for(int i = x; i; i -= lowbit(i))  sum += t[i];
    return sum;
}

题单

洛谷 $P3374$ 【模板】树状数组 1
【基础模板】

$HDU1166$ 敌兵布阵
【单点修改+区间和查询】

$AcWing$ $788$. 逆序对的数量 $P1908$ 逆序对
【树状数组+逆序对+离散化,与上一题是同一题】

$POJ$ $3067$ $Japan$
【二维逆序对,结构体按一维由小到大，二维由小到大排序，不使用离散化】

$P1966$ [$NOIP2013$ 提高组] 火柴排队
【逆序对，离散化，位置+高度，按高度由小到大排序，倒序枚举就是由高到低，逐个进入树状数组，不断取位置比我大，但在我左侧的数量】

$POJ$ $2299$ $Ultra-QuickSort$
【不管是否需要，一律原地静态数组离散化,由小到大排序，配合$lower\_bound$,比我小，并且序号在我后面的统计个数】
【不用由大到小排序，那样配合$lower\_bound$会出问题，不建议】

$P2345$ [$USACO04OPEN$] 奶牛集会
【两个树状数组，一个用于维护奶牛的坐标和，一个用于维护奶牛前后的个数，数学分析式子】

$P3368$ 【模板】树状数组 $2$
【区间修改,单点查询,树状数组维护差分，求和就是变化值，$sum(k)+a[k]$】

$AcWing$ $242$. 一个简单的整数问题
【区间修改,单点查询,树状数组维护差分，求和就是变化值，$sum(k)+a[k]$】

$LOJ$ $10117$「一本通 $4.1$ 练习 $2$」简单题
【区间修改,单点查询,树状数组维护差分，求和就是变化值，$sum(k)+a[k]$】

$LOJ$ $10115$. 「一本通 $4.1$ 例 $3$」校门外的树
【左右括号问题，两个树状数组，分别记录左括号个数，右括号个数】

$AcWing$ $241$ 楼兰图腾
【树状数组+及时统计并用数组记录+动态单点修改】

$POJ$ $2352$ $Stars$
【扫描线+树状数组】

注：其实【区间修改，区间查询】还得是线段树，用树状数组+推公式的办法也可以做，但不是正解：

$AcWing$ $243$. 一个简单的整数问题2
【区间修改、区间查询(利用差分+推公式)】

$P3372$ 【模板】线段树$1$
【与上面的就是一个题】

$POJ$ $3468$ $A$ $Simple$ $Problem$ $with$ $Integers$
【与上面的就是一个题】

$HDU$ $1754$ $I$ $Hate$ $It$
【树状数组求最大最小值模板题】

$POJ$ $3264$ $Balanced$ $Lineup$
【树状数组求最大最小值,在上面的题目上同时加上求最大和求最小】

$AcWing$ $244$. 谜一样的牛
【逆向思考+树状数组维护前缀和+二分快速查找$sum=h[i]$】

$HDU$ $2852$ $KiKi's$ $K-Number$
【逆向思考+树状数组维护前缀和+二分快速查找】

二维树状数组

一、二维树状数组

二维树状数组，其实就是一维的树状数组上的节点再套个树状数组，变成了二维树状数组。

const int N = 1e3 + 10;
int c[N][N], n, m;

#define lowbit(x) (x & -x)

void add(int x, int y, int v) {
    for (int i = x; i <= n; i += lowbit(i))
        for (int j = y; j <= m; j += lowbit(j))
            c[i][j] += v;
}

LL query(int x, int y) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        for (int j = y; j; j -= lowbit(j))
            res += c[i][j];
    return res;
}

二、单点修改，区间查询

$LOJ$ #$133$. 二维树状数组 1：单点修改，区间查询

给出一个 $n × m$ 的零矩阵 $A$ ，你需要完成如下操作：

$1$ $x$ $y$ $k$ ：表示元素 $A_{x , y}$ 增加 $k$
$2$ $a$ $b$ $c$ $d$: 表示询问左上角为 $(a,b)$ ，右下角为 $(c,d)$ 的子矩阵内所有数的和

单点增加，因此可以直接加上就可以了

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 5000; // 2^(12)=4096

int n, m;

LL c[N][N];
#define lowbit(x) (x & -x)
void add(int x, int y, int d) {
    for (int i = x; i < N; i += lowbit(i))
        for (int j = y; j < N; j += lowbit(j))
            c[i][j] += d;
}
LL query(int x, int y) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        for (int j = y; j; j -= lowbit(j))
            res += c[i][j];
    return res;
}

int main() {
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    int opt;
    while (cin >> opt) {
        if (opt == 1) {
            int x, y, d;
            cin >> x >> y >> d;
            add(x, y, d);
        } else {
            int x1, y1, x2, y2;
            cin >> x1 >> y1 >> x2 >> y2;
            cout << query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1) << '\n';
        }
    }
    return 0;
}

三、区间修改，单点查询

$LOJ$ #$134$. 二维树状数组 2：区间修改，单点查询

给出一个 $n × m$ 的零矩阵 $A$ ，你需要完成如下操作：

$1 \, a \, b \, c \, d \, k$：表示左上角为 $(a,b)$ ，右下角为 $(c,d)$ 的子矩阵内所有数都自增加 $k$；
$2 \, x \, y$ ：表示询问元素 $A_{x,y}$ 的值。

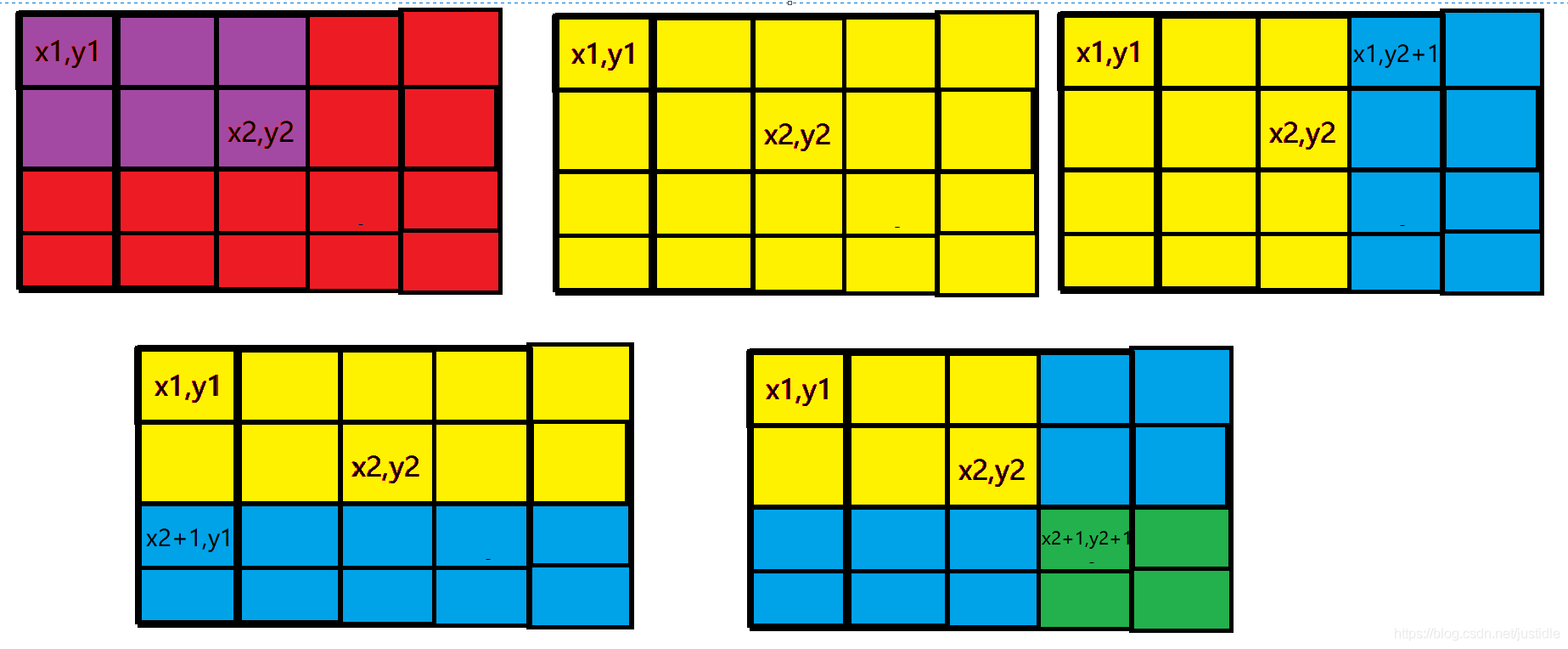
只需要利用一个二维树状数组，维护一个二维差分数组，单点查询即可。

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 5000;
int n, m;

LL c[N][N];
#define lowbit(x) (x & -x)
void add(int x, int y, int v) {
    for (int i = x; i <= n; i += lowbit(i))
        for (int j = y; j <= m; j += lowbit(j))
            c[i][j] += v;
}
LL query(int x, int y) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i))
        for (int j = y; j; j -= lowbit(j))
            res += c[i][j];
    return res;
}

int main() {
    //加快读入
    ios::sync_with_stdio(false), cin.tie(0);

    cin >> n >> m;
    int op;
    while (cin >> op) {
        if (op == 1) {
            int x1, y1, x2, y2, d;
            cin >> x1 >> y1 >> x2 >> y2 >> d;
            //二维差分
            add(x1, y1, d);
            add(x1, y2 + 1, -d);
            add(x2 + 1, y1, -d);
            add(x2 + 1, y2 + 1, d);
        } else {
            int x, y;
            cin >> x >> y;
            cout << query(x, y) << '\n';
        }
    }
    return 0;
}

四、区间修改，区间查询

$LOJ$ #$135$. 二维树状数组 $3$：区间修改，区间查询

给定一个大小为 $N × M$ 的零矩阵，直到输入文件结束，你需要进行若干个操作，操作有两类：

$1 \, a\, b\, c\, d\, x$，表示将左上角为 $(a,b)$ ，右下角为 $(c,d)$ 的子矩阵全部加上 $x$；
$2\, a\, b\, c\, d\,$ , 表示询问左上角为 $(a,b)$ ，右下角为 $(c,d)$ 为顶点的子矩阵的所有数字之和。

考虑前缀和 $sum[i][j]$ 和原数组 $a$ , 差分数组 $d$ 之间的关系。

首先$\displaystyle sum[i][j]=\sum_{x=1}^i\sum_{y=1}^ja[x][y]$ (二维前缀和)

又由于$\displaystyle a[x][y]=\sum_{u=1}^x\sum_{v=1}^yd[u][v]$ (差分数组与原数组关系)

所以：

\[\displaystyle sum[i][j]=\sum_{x=1}^i\sum_{y=1}^j\sum_{u=1}^x\sum_{v=1}^yd[u][v] \]

可以说是非常复杂了......

统计$d[u][v]$出现次数

从$a[1][1]$到$a[i][j],d[1][1]$全都要出现一次，所以有$i×j$个$d[1][1]$，即$d[1][1]×i×j$
从$a[1][1]$到$a[i][j]$,$d[1][2]$出现了多少次呢？头脑中出现一个二维差分转原数组(本质就是一个原数组转二维前缀和)的图像:
- $i=1,j=1$时, $d[1][2]$就没有出现
- $i=1,j=2$时, $d[1][2]$出现$1$次
- ...
- $i=2,j=1$时, $d[1][2]$就没有出现
- $i=2,j=2$时, $d[1][2]$出现$1$次
- ...

总结一下：

$d[1][2]×i×(j−1)$
$d[2][1]×(i−1)×j$
$d[2][2]×(i−1)×(j−1)$
等等……

所以我们不难把式子变成：

\[sum[i][j]=\sum_{x=1}^i\sum_{y=1}^j \begin{bmatrix}d[x][y]×(i+1−x)×(j+1−y)\end{bmatrix} \]

展开得到：

\[sum[i][j]=\sum_{x=1}^i\sum_{y=1}^j \begin{bmatrix}d[x][y]\times (i+1)\times (j+1)-d[x][y]\times x \times (j+1)-d[x][y]\times (i+1) \times y+d[x][y]\times xy \end{bmatrix} \]

也就相当于把这个式子拆成了四个部分：
$\displaystyle ① (i+1)(j+1)×\sum_{x=1}^i\sum_{y=1}^jd[x][y] \\ ② −(j+1)×\sum_{x=1}^i\sum_{y=1}^j(d[x][y]⋅x) \\ ③ −(i+1)×\sum_{x=1}^i\sum_{y=1}^j(d[x][y]⋅y) \\ ④ \sum_{x=1}^i\sum_{y=1}^j(d[x][y]⋅xy)$

所以我们需要在原来 $C_1[i][j]$ 记录 $d[i][j]$ 的基础上，再添加三个树状数组：

$C_2[i][j]$ 记录 $d[i][j]⋅i$
$C_3[i][j]$ 记录 $d[i][j]⋅j$
$C_4[i][j$] 记录 $d[i][j]⋅ij$

这样一来，就能通过数组$a[i][j]$的差分数组$d[i][j]$来得到$a[i][j]$的前缀和数组$sum[i][j]$。

最后，易知$(x_1,y_1)$到$(x_2,y_2)$的矩阵和就是一个标准的二维前缀和公式，等于$$\large sum[x_2][y_2]−sum[x_2][y_1−1]−sum[x_1−1][y_2]+sum[x_1−1][y_1−1]$$

$Code$

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2050;

int n, m;
LL c1[N][N], c2[N][N], c3[N][N], c4[N][N];
#define lowbit(x) (x & -x)

// 维护四个树状数组
void add(int x, int y, int v) {
    for (int i = x; i < N; i += lowbit(i))
        for (int j = y; j < N; j += lowbit(j)) {
            c1[i][j] += v;
            c2[i][j] += v * x;
            c3[i][j] += v * y;
            c4[i][j] += v * x * y;
        }
}

// 查询左上角为(1,1)右下角为(x,y)的矩阵和
LL query(int x, int y) {
    LL res = 0;
    for (int i = x; i; i -= lowbit(i)) {
        for (int j = y; j; j -= lowbit(j)) {
            res += (x + 1) * (y + 1) * c1[i][j];
            res -= (y + 1) * c2[i][j];
            res -= (x + 1) * c3[i][j];
            res += c4[i][j];
        }
    }
    return res;
}

int main() {
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    int op;
    while (cin >> op) {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        if (op == 1) {
            int d;
            cin >> d;
            // 维护四个数组
            add(x1, y1, d);
            add(x1, y2 + 1, -d);
            add(x2 + 1, y1, -d);
            add(x2 + 1, y2 + 1, d);
        } else
            cout << query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1) << '\n';
    }
    return 0;
}

$POJ$ $2155$ $Matrix$
【二维树状数组】

posted @ 2022-04-13 11:40 糖豆爸爸阅读(150) 评论(0) 收藏举报

刷新页面返回顶部

蒟蒻豆进阶之路