2025.9 做题笔记
「我存在为你而歌」
——洛天依《心声》
MX 练石 2025 NOIP #2 T3
思维难度:\(\color{#3498DB} 蓝\) *2000
喜欢的题。真的很巧妙。
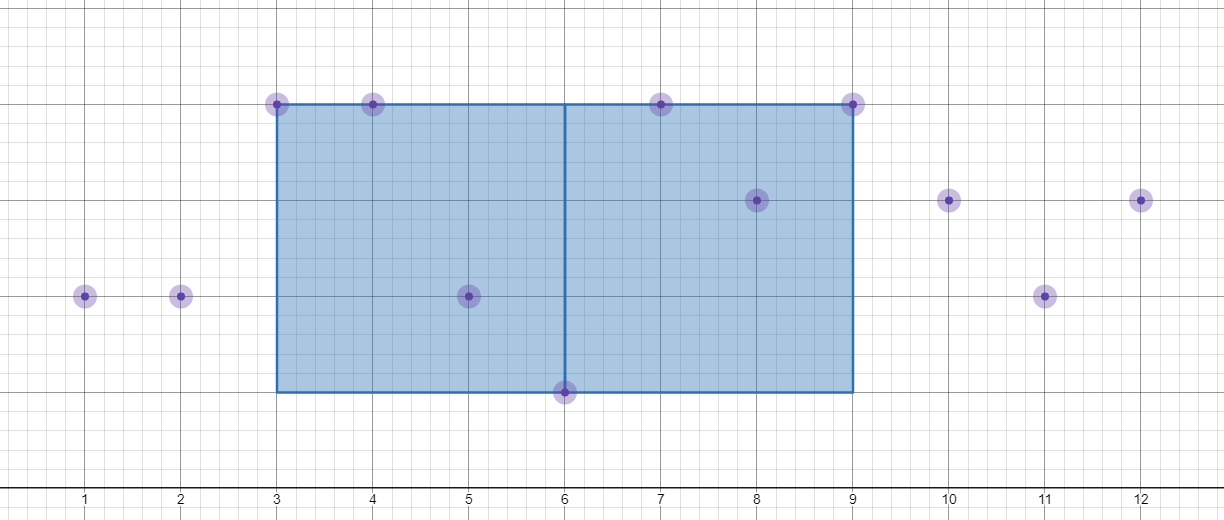
先进行一些观察。容易发现 \(a_1 , a_n\) 以及满足 \(a_j = \max \{ a_i \}\) 或 \(a_j = \min \{ a_i \}\) 的 \(a_j\) 一定不会被删除,令后者的点集为 \(S\),那么 \(x\) 坐标 \(\displaystyle ( \min _{(x,y) \in S} \{ x \} , \max _{(x,y) \in S} \{ x \} )\) 这个区间内的点一定会被删除,例如(矩形表示删除的部分):
那么只需要处理两边的点就可以了,两者是等难的,所以只考虑左边。令被删除矩形的左边界的 \(x\) 坐标为 \(L\)。继续观察,容易发现不和 \(a_1\) 在同一条水平线上的点一定会被删除(随便在矩形的边框上选个点,再加上 \(a_1\))。
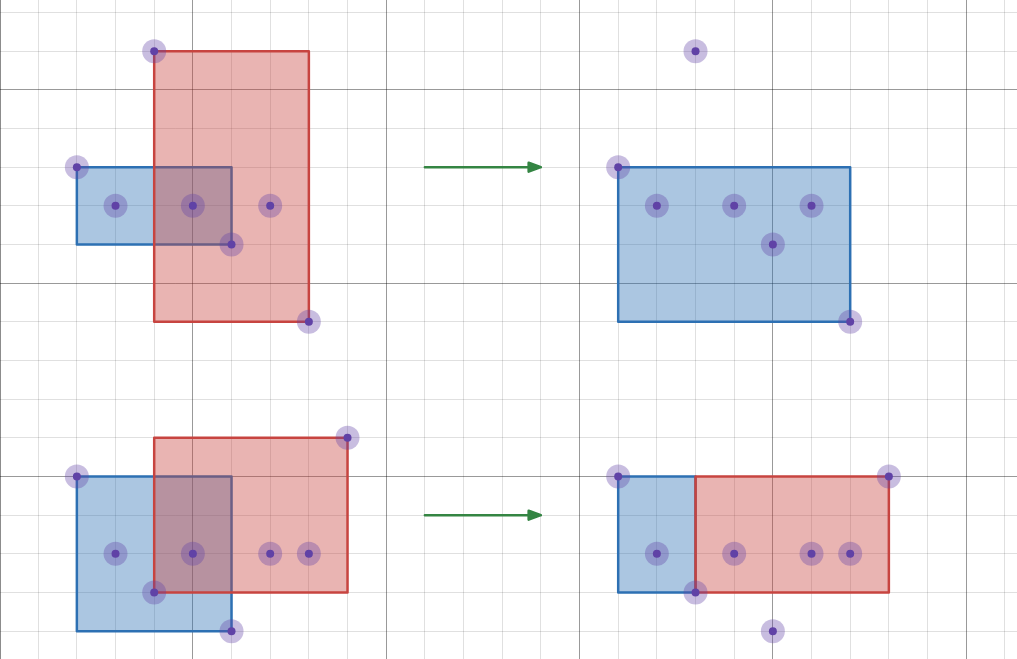
所以只需要考虑 \(1 \sim L\) 内和 \(a_1\) 在同一条水平线上的点,令这些点为关键点。先看看这些点是如何被删除的呢?画一下可以发现,如果点 \(i\) 被删除,那么一定是 \(i\) 左边有一个 \(> a_i\),右边有一个 \(< a_i\) 的点导致的(或者换一下,左边小右边大)。但是继续画一画会发现可能出现选择的矩形有交的情况,这是不好处理的,但是继续画,又会发现每个有交的情况都可以等价转化成无交的情况!例如:
这样就方便了很多,考虑 dp,令 \(f_{i,j}\) 为前 \(i\) 个点(仅包括关键点)保留了 \(j\) 个是否可行。转移考虑是否删除第 \(i+1\) 个点,有:
- 若不删除。则 \(f_{i,j} \to f_{i+1,j+1}\)。
- 若删除。直接枚举 \(i,i+1\) 之间的非关键点 与 后面哪个关键点 \(k,k+1\) 之间的非关键点组成矩形,有 \(f_{i,j} \to f_{k,j}\)。此时需要满足的条件,形式化地来讲,就是 \(i,i+1\) 之间存在 \(>a_1\) 的点,\(k,k+1\) 之间存在 \(< a_1\) 的点(同样,也可以反过来)。
直接枚举是 \(O(n^3)\) 的。考虑 bitset 优化,可以发现第二种转移对应的 \(j\) 都是相同的,而且仅需要 \(i,k\) 就可以确定是否转移,所以可以枚举 \(i,k\),转移直接按位或就可以了。
复杂度 \(O(\frac {n^3} w)\)。
不得不说是真的神。
天依宝宝可爱!
MX 练石 2025 NOIP #2 T4
思维难度:\(\color{#52C41A} 绿\) *1900
比上一题简单一点。
因为求的是形如 \(\sum _{1 \le l \le r \le n} f(l,r)\) 的式子,而且 \(m\) 很小,所以考虑分治。
很自然地可以想到,需要维护一个数据结构,支持对于一个矩阵的并查集(记录题目中的连通块),往它左边加一列(仅考虑分治区间靠左的那一部分)。那最后什么是需要的呢?因为我们要把整个分治区间 \([l,r]\) 分成 \([l,mid] , (mid,r]\) 之后,需要在 \(mid\) 处合并两边的答案,所以我们只需要维护最右侧一列的并查集信息就可以了。当然同时还要维护连通块个数,这个是容易的。
那么先假设我们有了这么一个数据结构,考虑如何低复杂度地合并。可以注意到,对于所有 \([l \sim mid,mid]\),其构成的不同右侧并查集只有 \(O(m)\) 个,所以每个不同并查集可以放到一起处理,这样就只需要进行 \(O(m^2)\) 次合并操作了。
然后考虑具体该怎么做。根据答案应该如何计算来推出我们需要维护哪些东西。
- 可以发现在合并之前最右边的点不在 \(mid\) 上的连通块是确定的,所以要维护这种连通块的个数(记为 \(s\))。做法比较显然,在加列的时候看看新加的一列里有几个没有和右侧合并的连通块即可。
- 合并时,对于每种可能的左右组合需要计算有多少个,所以要维护右侧并查集相同的区间个数(记为 \(c\))。
- 剩下的就是 \(mid,mid+1\) 两个并查集的合并了,这个只要前面记录了每个不同并查集,随便搞搞就可以了。记合并后连通块个数为 \(t\)。
计算答案直接乘法原理,显然就是:
关于这个数据结构的维护,先写个并查集上去,发现唯一不好处理的地方在于如何维护右侧并查集是否改变。可以考虑从右往左给 \([l,mid]\) 中的点编号,每次合并的时候,钦定当父亲的点为编号较小的点,这样就可以保证最右侧点的父亲一定不会跑到左侧,于是就好维护了。当然这样就不能按秩合并了。
最后分析复杂度。
- 加列的复杂度大概是 \(O(m \log m)\) 的(不在 log 里乘上 \(n\) 是因为并查集根本跑不满,而且也不是每轮分治都是 \(n \times m\) 大小的并查集,所以可以忽略掉了);因为是分治所以每一列会被加入 \(\log n\) 次。所以这部分的复杂度为 \(O(nm \log n \log m)\)。
- 合并的复杂度是 \(O(m \log m)\),一共 \(O(m^2)\) 对需要合并,分治一共会进行 \(\le 2n\) 轮。所以这一部分的复杂度为 \(O(n m^3 \log m)\)。
总复杂度 \(O(n m^3 \log m + nm \log n \log m)\)。
不过实际上,做到这里就可以发现,分治其实是不需要的,直接在原序列上,分别从左到右、从右到左扫一遍。(单独考虑从左到右)还是因为不同的右侧并查集只有 \(O(m)\) 个,所以在右侧右边加列,并同时维护上面那些信息的复杂度是 \(O(m^2 \log m)\) 的,总复杂度 \(O(n m^2 \log m)\)。
但是分治写法正好可以练一下这种比较复杂的分治的代码能力,所以我写的是分治写法。
但是我也不知道为什么会 WA 啊……有时间再调吧,大样例是没过的 submission
天依宝宝可爱!
CF1140F | 线段树分治
思维难度:\(\color{#FFC116} 黄\) *1500
可以发现,如果吧每个 \(x_i , y_j\) 都抽象成一个二分图上的节点,那么对于同一个 \(y_j\) 连接的所有 \(x_{i1} , x_{i2} , \ldots\),再由其中一个 \(x_{i1}\) 连出去的 \(y_j'\),都可以构成 \((x_{i1} , y_j) , (x_{i-2} , y_j) , (x_{i1} , y_j')\) 这样的三元组,于是 \((x_{i2} , y_j')\) 就会被加入图中。推广一下可以发现,原二分图中在同一连通块内的点,均可在满足二分图的前提下两两相连,令两个点集分别为 \(S_x , S_y\),那么这个连通块所贡献的答案就是 \(|S_x| \times |S_y|\),可以发现这个东西是可以用并查集维护的。
但是还有删点操作,去看看题解可以发现是清一色的线段树分治,学一下,就会了。
线段树分治
对于这样一类问题,可以用线段树分治解决:
- 在一条长度为 \(n\) 时间轴上有 \(m\) 次操作,每个操作生效的时间区间给定为 \([l_i , r_i]\)。
- 对于 \(q\) 次询问,每次询问一个点,求在这个点生效的所有操作的贡献之和。
具体地,我们在时间轴上建一棵线段树,线段树的每个节点上存 生效区间完全覆盖这个节点 的操作,且在父节点存过的操作不再往子节点上存,那么一个操作显然最多只会被切成 \(\log n\) 段。
对于询问,先把所有询问离线下来并排序,然后 dfs 整棵线段树:
- 进入一个节点时,进行这个节点上存储的操作。
- 如果是叶子节点,则记录答案。
- 否则继续遍历有询问的子节点。
- 退出一个节点时,撤销这个节点上存储的操作,所以我们用于计算答案所维护的东西必须是支持撤销的。
那么这个题的做法就很显然了,线段树分治 + 可撤销并查集即可。
天依宝宝可爱!
CF1197F
思维难度:\(\color{#52C41A} 绿\) *1900
省流:把 SG 函数值丢到 dp 状态里面。
由 SG 函数,每个纸条之间是独立的,分别计算每个纸条的答案然后最后异或起来即可。因为一个状态只能由它前面的 \(3\) 个状态转移,所以一个状态的 SG 值最大为 \(3\),这样暴力 dp 每个纸条 SG 值的异或和的复杂度就是正确的。
那么单独对一个纸条考虑。
容易注意到状态的转移只与 \(i-2,i-1,i\) 三个状态有关,所以考虑把这三个状态的 SG 值丢到 dp 的状态里(此处两个「状态」不是同一个东西,前者是游戏的状态,后者是 dp 的状态)。
令 \(f_{i,a,b,c}\) 为纸条的前 \(i\) 个位置,第 \(i,i-1,i-2\) 个位置的 SG 值为 \(a,b,c\) 的方案数,那么显然有转移:
其中 \(SG(i+1)\) 是可以直接算的,即(此处用 \(t\) 代替了题目中的 \(f\),并采用 0-index 表示):
显然直接转移不可以,但是注意到不为 \(-1\) 的点很少,所以考虑矩阵优化。可以发现相同的点(指点上的数字相同)的转移矩阵是相同的,所以可以对于一段连续的 \(-1\) 用矩阵快速幂优化,对于不为 \(-1\) 的点单独矩阵乘向量。
注意到复杂度是 \(O((n+m) k^3 \log V + mk^2)\) 的(\(k = 4^3\)),所以要预处理转移矩阵的 \(2^k\) 次幂,把 \(O(k^3)\) 的矩乘变成 \(O(k^2)\) 的矩阵乘向量。
天依宝宝可爱!
CF632F
思维难度:\(\color{#FFC116} 黄\) *1500
注意到满足前两个条件之后,可以看做一个邻接矩阵,由第三个条件可得:
也就是在图上 \((i,j)\) 这条边的边权不是包含 \((i,j)\) 的任意一个环的严格最大值。
于是跑一遍 kruskal 求 MST 就可以解决了。
天依宝宝可爱!
CF620F
思维难度:\(\color{#FFC116} 黄\) *1400
原来 trie 还能当线段树用的吗?哦结构比较相似,是能的qwq
注意到奇怪的数据范围和时限,启示我们用根号算法。
显然是莫队,然后因为要维护 max 所以是回滚莫队。
于是问题就变成了如何快速求 \(a_r\) 与莫队区间包含的 \(a_i\) 的最小 \(f\)。先转化为前缀和,那么就是:
看着 \(a_i-1\) 比较不顺眼,换掉:
求异或最大值考虑 trie。于是开两棵 trie,一棵维护 \(s_{a_i}\),一棵维护 \(s_{a_i} \oplus a_i\)。那么一个询问就可以拆成两半,分别为:
- 在第一棵 trie 上,求满足 \(a_i \le a_r\) 的点中与 \(s_{a_r}\) 的异或最大值。
- 在第二棵 trie 上,求满足 \(a_i \ge a_r\) 的点中与 \(s_{a_r} \oplus a_r\) 的异或最大值。
显然两者等难,故只考虑前者怎么做。
注意到 trie 是不容易精准遍历所有小于某个数的位置的。所以需要另外维护一些东西,具体地,我们维护每个节点所代表的子树内编号最小(编号即 \(a_i\) 的值)的点,类似线段树地更新,查询的时候就容易确定要往哪个儿子转移了。
时间复杂度 \(O((n+q) \sqrt n \log V)\)。
经过测试,块长取 \(650\) 左右最快,接近 \(\sqrt n\) 的 \(3\) 倍,不知道为什么。块长太大 WA 了也不知道为什么。
| 块长 | 用时 |
|---|---|
| \(150\) | 9764 ms |
| \(\bf 224\)(\(\sqrt n\)) | 7577 ms |
| \(350\) | 5968 ms |
| \(450\) | 4906 ms |
| \(550\) | 3999 ms |
| \(630\) | 3906 ms |
| \(\bf 650\) | 3687 ms |
| \(665\) | 3890 ms |
| \(680\) | WA on #17 |
| \(700\) | WA on #17 |
submission。显然上面的就是()
天依宝宝可爱!
MX 练石 2025 NOIP #4 T1 | 笛卡尔树
思维难度:\(\color{#F39C11} 橙\) *1200
笛卡尔树:一个 \(O(n)\) 预处理,在最值分治中 \(O(1)\) 求每个分治区间的最值的东西。直接看 OI-wiki。
对于序列 \(a_i\) 构建笛卡尔树,具有性质:
- 是一棵二叉树。
- \(i\) 左边的元素都在 \(i\) 的左子树内,右边同理。
- \(i\) 是其子树内的最值。
- 一棵子树内的下标是一个连续区间。
- 或者说,在最值分治中,\(i\) 的子树就是 \(a_i\) 作为最值的区间,\(i\) 的左右儿子分别是 \(i\) 下面的两个分治区间的最值位置。
- 若 \(a_i\) 互不相同,则笛卡尔树的形态唯一。若 \(a_i\) 中可能出现相同元素,则在最值分治中,笛卡尔树的节点上是非严格最值。
这个题,直接分治,对于每个点暴力枚举可能的区间,就过了。。
为什么呢?因为根据人类直觉,最值为 \(x\) 且长度为 \(x\) 的区间并不是很多,远远达不到 \(O(n^2)\) 的级别,实际上据说只有 \(O(n \log n)\)。
题外话:这场 AB 暴力都可过,C 暴力 70pts 随便分治一下就能过,出题人太良心了,好评。
天依宝宝可爱!
AT_abc191_f
思维难度:\(\color{#F39C11} 橙\) *1100
喜提转化很会但是最后 rz 问题不会求。
问题:求大小为 \(n\) 的集合 \(S\) 的任意子集 gcd 可能结果数。其中 \(n \le 2000\),值域是 \(10^9\)。
注意到若某个子集包含一个数 \(x\),那么该子集的 gcd 一定是 \(x\) 的因数。又因为 \(S\) 内所有数的因数个数和只有 \(O(n \log V)\) 个,所以暴力枚举每个可能的因数 \(d\),看看包含 \(d\) 这个因数的数的 gcd 是否 \(=d\),即可判断 \(d\) 是否可能成为子集的 gcd。这个过程可以 map 实现。
天依宝宝可爱!
AT_abc209_f | 插入 dp
思维难度:\(\color{#FFC116} 黄\) *1400
奇怪的 dp 方式又增加了。
注意到对于相邻两个位置 \(a_i , a_{i+1}\),两者之中较大的那个一定先选,如果同样大则选哪个都可以。
于是问题就转化成了给定相邻两个元素之间的大小关系(大于、小于、均可),求满足这些关系的 \(1 \sim n\) 的排列数量。
转化一下,原条件是「在位置 \(i\) 上填的数必须大于(小于)在 \(i-1\) 上填的数」,那么如果把填的数当作下标升序排序,就等价于「\(i\) 在序列中的排名必须比 \(i-1\) 靠后(靠前)」。
插入 dp。用于解决让你算一个排列的方案数,然后这个排列满足某某大小关系,不过不规定元素的确切的值。
令 \(f_{i,j}\) 表示前 \(i\) 个数构成 \(1 \sim i\) 的合法排列,且 \(i\) 的排名为 \(j\) 的方案数。注意这里的元素位置是在 \(1 \sim i\) 这个排列中相对位置,并不是最终排列中的位置。
那么转移:
-
若要求 \(p_i < p_{i-1}\),则枚举 \(i-1\) 在 \(1 \sim i-1\) 中的相对位置,有:
\[f_{i,j} = \sum _{k=j} ^{i-1} f_{i-1,k} \]解释一下为什么是这个。首先 \(i\) 一定是在 \(i-1\) 前面的,所以只要 \(i-1\) 前面有 \(\ge j\) 个元素,那么就可以把 \(i\) 插入到 \(i-1\) 前面一个位置,使得 \(i\) 的排名也 \(\ge j\)。
-
若要求 \(p_i > p_{i-1}\),同理,有:
\[f_{i,j} = \sum _{k=1} ^{j-1} f_{i-1,k} \] -
若没有要求,那就随便了,把 \(i\) 放到任意位置都可以,有:
\[f_{i,j} = \sum _{k=1} ^{i-1} f_{i-1,k} \]
前缀和优化一下就可以 \(O(n^2)\) 了。
双倍经验(实际上这个才是板子):AT_dp_t。
天依宝宝可爱!
AT_abc175_f | 串串自动机
思维难度:\(\color{#52C41A} 绿\) *1700
抛开 ACAM 不谈,让我们来重新认识一下自动机这个东西(严格来说这里指的是有限状态自动机):
- 可以表示为一张有向图(有时候是 DAG)。
- 有向图中的每个节点代表自动机上的一个状态,且状态是有限的。
- 有向图中的每条边代表一种转移,可以从一个状态转移到另一个状态。
在串串相关题目中:
- 通常一个自动机由一些模式串构建,每个模式串加入到自动机里 都是 一些加点和加边的过程。
- 一般看起来很难处理的问题,答案需要有多个串相互联系得到,而且串与串直接的联系比较难以显示地枚举得到,这样的问题可以尝试构造自动机解决。
- 有时候,需要在跑完模式串的基础上,再加一些起点和终点,以便于解题。
回到这个题,因为要找回文串并且还一个串能选任意次,是很麻烦的,于是考虑构造自动机。
可以发现,在把两个串拼到一起的时候,如果得到的串能通过一些操作得到答案,那么得到的串已经满足回文的部分就可以删掉了,例如:
在合并串 \(\tt \color{#EEAADD} cba\) 和 \(\tt \color{#66CCFF} abcde\) 的时候,可以发现得到的 \(\tt {\color{#EEAADD} \underline{cba}} {\color{#66CCFF} \underline{abc} de}\) 中,\(\tt {\color{#EEAADD} \underline{cba}} {\color{#66CCFF} \underline{abc}}\) 已经满足回文,所以只需要在串的左边添加串使得其可以和 \(\tt \color{#66CCFF} de\) 满足回文即可(其实这里是不对的,一会儿说),于是 \(\tt {\color{#EEAADD} \underline{cba}} {\color{#66CCFF} \underline{abc}}\) 就可以被删掉,只留下一个后缀 \(\tt \color{#66CCFF} de\)。
这里强调后缀是为了保证只能在左边加串,因为即使在右边加了 \(\tt ed\) 这个串,那么整个串就变成了 \(\tt {\color{#EEAADD} cba} {\color{#66CCFF} abcde} ed\) 并不是回文的。同时,加的串必须和剩下的串的最左边开始匹配,例如加入 \(\tt e\) 时,整个串是 \(\tt e {\color{#EEAADD} cba} {\color{#66CCFF} abcde}\),显然已经不可能使 \(\tt \color{#66CCFF} d\) 满足回文了。前缀同理。
不过,并不是以后永远不能在右边加串了,例如:
如果在左边加入一个 \(\tt \color{#FFDDAA} fged\),那么那么整个串就是 \(\tt {\color{#FFDDAA} fged} {\color{#EEAADD} cba} {\color{#66CCFF} abcde}\),按照上面的规则删串之后就剩下了前缀 \(\tt \color{#FFDDAA} fg\),可以在右边继续加串使其满足回文。
同时,在加入 \(\tt \color{#FFDDAA} fged\) 后,仅看当前这一步的串 \(\tt {\color{#FFDDAA} fged} \color{#66CCFF} de\),删除之后剩下的也是前缀 \(\tt \color{#FFDDAA} fg\)。
所以,我们关心的是在一次操作结束后剩下的串是什么、是删除前的串的前缀还是后缀,然后再根据后缀或前缀往左边或右边加串即可得到下一个状态。
可以发现按照这样的规则,每个状态是没有后效性的,所以就可以拍到自动机上去跑。
那自动机上放哪些状态呢?容易证明每次操作剩下的串一定是一个模式串 \(s_i\) 的前缀或后缀,因为数据范围比较小,所以直接把每个 \(s_i\) 的所有前后缀都放到自动机的状态里即可,可以发现最多只有 \(2000\) 个状态。
转移考虑对于每个状态,暴力枚举往它的左边(右边)加入哪个 \(s_i\),即可确定转移的方向以及代价。
然后,可以新建一个起点和一个终点。对于每个 \(s_i\),建一条由起点连向 \(s_i\) 的边权为 \(c_i\) 的有向边。对于自动机上每个已经回文的状态,建一条连向终点的边权为 \(0\) 的边。
于是答案就是自动机(有向图)上从起点到终点的最短路,直接跑 dij 即可。
最开始做的时候的一个疑问:
一开始,我是没有关注前缀还是后缀的,因为例如在合并串 \(\tt cba\) 和 \(\tt abcde\) 的时候,不仅可以这样 \(\tt ??? {\color{#EEAADD} \underline{cba}} {\color{#66CCFF} \underline{abc} de}\),还可以这样 \(\tt {\color{#66CCFF} \underline{abc} de} ??? {\color{#EEAADD} \underline{cba}}\),其中 \(\tt ?\) 表示需要继续填串的位置。所以往 \(\tt de\) 左边或右边加串都是可以的。然后就理所当然的推广了,而且甚至就 WA 了 \(2\) 个点。
但是当合并的串一多,就不成立了。例如在合并 \(\tt \color{#66CCFF} abcdefg\)、\(\tt \color{#EEAADD} cba\)、\(\tt \color{#FFDDAA} gf\) 的时候,如果按照上面第二种方法,第一步之后的结果为 \(\tt {\color{#66CCFF} \underline{abc} defg} ??? {\color{#EEAADD} \underline{cba}}\) 即 \(\tt {\color{#66CCFF} defg} ???\);那么第二步就可以 \(\tt {\color{#66CCFF} de \underline{fg}} {\color{#FFDDAA} \underline{gf}}\) 得到 \(\tt \color{#66CCFF} de\) 了。但是这时原串 \(\tt {\color{#66CCFF} abcdefg} {\color{#FFDDAA} gf} {\color{#EEAADD} cba}\) 是无法得到这个结果的。
天依宝宝可爱!
CF1375G
思维难度:这个真的评不了
有简单好想的换根 dp 做法,但是并不优美。
不过能想到二分图的诗人?这真的是正常人类能想得到的?
但是如果想到了,那就比换根 dp 还简单了。问题是想不到。所以不如套路地换根 dp(确信
一个可能想到的方式:注意到每次操作需要跨一个点(所以正好是操作颜色相同的两个点),然后注意到每次操作只会改变点 \(a\) 的颜色,又因为最后要求菊花图,可能可以想到。
欸我换根 dp 式子推错了怎么还过了?
详情见题解。
submissions:换根 dp、错误的换根 dp、黑白染色
天依宝宝可爱!
CF1515F
思维难度:\(\color{#FFC116} 黄\) *1400
乱搞过掉了。好玩。
考虑一个暴力的过程,就是每次暴力枚举所有边,选所连的两个连通块的权值和最大的边。不能预先排序的原因是在连通块合并后连通块的权值会改变。
但是注意到,每次合并只会改变两个连通块的权值,所以事实上预先排序再遍历边集,是能连上不少边的。
所以一次不行就多跑几次,这样就可以尽可能地连上所有能连的边了。
但是这是很容易卡的,构造一条链,再令 \(a_1\) 为一个极大值,其他都是 \(0\),就卡掉了。所以这样会 WA on #11。
难道真的没办法了吗?
有的!
我们充分发扬人类智慧,发现和点权大的点距离近的点更有可能被连上,所以可以给每个点一个估价函数 \(w_i\) 表示这个点被连上的可能性大小。
随便 bfs 一下求个 \(w_i\)(规则怎么定应该都可以),再按照这个对边进行排序就轻松过掉了,跑了 2108 ms。
实际上应该还能跑更快的,因为我估价函数是瞎写的(
哦对了,还是说下正解吧。注意到 \(\sum a_i \ge (n-1) x\) 一定有解,鸽巢原理证即可。但是不会构造。
看题解,发现对于任意一棵生成树,都存在一种合法的修建方案。证明是在 dfs 过程中,如果 \(val_u + val_v \ge x\) 则直接连边,否则把这条边放到最后连。构造方式也显而易见了。
猜结论能力有待提升。
天依宝宝可爱!
CF1450F
思维难度:\(\color{#52C41A} 绿\) *1800
感觉好像是不难的题啊……我怎么不会呢……
还是注意力不够。
先把无解判掉,只考虑有解的情况。
显然要考虑相邻且相同的两个数,这个地方必须断开。
那么整个序列就被切了 \(k\) 刀,分为了 \(k+1\) 段。
然后就是需要注意到同一段内正序逆序不影响答案,且把每一段看成一个整体后,重排整个序列使其合法的所有方案代价都是 \(k\)。这个显然,因为你两个本来相邻的段一定不可以相邻嘛。
但是这时候不一定能得到合法的串,因为可能会出现一个数出现很多次的情况。
然后发现段内的重排一定不是更优的,所以只需要考虑端点处的取值。令 \(f(x)\) 为 \(x\) 作为端点的出现次数。
可以发现仅当 \(f(x) > k+2\) 的时候,只把段看作整体重排没有合法解。
又因为 \(\sum f(x) = 2k + 2\),所以只可能存在一个 \(x\) 使得 \(f(x) > k+2\)。
那就只能把段拆开了,显然拆的位置 \((a,b)\) 满足 \(a\ne x \land b \ne x\) 时最优。因为保证有解所以一定有足够的这样的位置让你拆。
拆一次会使得 \(k' \gets k+1\),所以拆 \(f(x) - (k+2)\) 次就可以合法了。
而且不会出现新的 \(x'\) 使得 \(f(x') > k'+2\),因为拆的位置 \((a,b)\) 一定满足 \(a \ne b\),所以 \(f(a)\) 和 \(f(b)\) 只会加一,但同时 \(k\) 也加一,所以 \(f(a)\) 和 \(f(b)\) 一定不会超限。
所以答案就是这个。
天依宝宝可爱!
CF1418G
思维难度:\(\color{#FFC116} 黄\) *1500
哦还可以哈希,忘了这事了。
显然是分治但是发现 cnt 数组不好算匹配,但是哈希掉就好算了(
然后可以发现根本不需要分治,直接枚举 \(r\),过程中维护所有前缀的哈希值丢到 umap 里;当 \(a_r\) 出现次数 \(>3\) 的数暴力删前缀直到 \(=3\) 就可以了。匹配就是前缀的哈希值相等,即 \([l,r]\) 合法当且仅当 \(h_r = h_{l-1}\),这个显然。
天依宝宝可爱!
CF1452F
思维难度:\(\color{#FFC116} 黄\) *1400
前面随便推推,到最后剩余一个 \(2^{x+i}\) 的时候,考虑应该操作 \(\le 2^x\) 的元素还是操作 \(2^{x+i}\) 的一部分。
因为 \(2^{x+i}\) 的 \(2^i-1 : 2^i\) 会被分解成 \(2^{i-1} : 2^{i-1} , 2^{i-1}-1 : 2^{i-1}\),且贪心地,一定会先走左子树再走右子树,于是可以判一下左子树的贡献与 \(k\) 的大小关系,然后递归到子问题。
调代码的过程:
-
WA on #2 Q5:忘记考虑在把一个数分解成若干个 \(2^x\) 之后,又会产生新的 \(1:1\)。
10 1 947459 389393 330193 923905 586112 633984 879912 105167 467236 366443 2 4 304758765299128961 -
WA on #2 Q151:只考虑了 \(1:1\) 个数 \(\ge k\) 的情况,忘记 \(1:1\) 个数 \(<k\) 但是当前处理的比值 \(>1\) 的情况。
10 1 370768 691341 211969 220375 136028 842276 746582 112475 578010 670433 2 0 283765227279777044 -
WA on #14 Q9559:草我第二步的时候怎么操作次数忘加了,怎么这还能过这么多点。还有就是递归边界的答案脑抽算错了。
10 1 4 1 5 1 4 0 2 0 0 2 2 1 269252 -
WA on #32 Q6515:不可以在非边界的时候直接把 \(1:1\) 做掉,因为最后可能会出现 \(4:2 , 1:2\) 这种情况,当 \(4:2\) 必选的时候,显然 \(1:2\) 比 \(1:1\) 更优。
10 1 0 1 1 0 0 0 1 0 1 1 2 1 77 -
WA on #32 Q1:套取数据的代码忘删了!
你懂不懂看到 \(\tt \color{#00B027} Accepted\) 那一刻的救赎感啊喂!!!
天依宝宝可爱!
AT_arc179_d
思维难度:\(\color{#52C41A} 绿\) *1700
贪心是容易 hack 的。所以是 dp。因为根节点影响答案,所以要换根,故先考虑根节点固定的情况。
一维状态显然是不够的,因为我们有棋子和门两个信息要记录;但是直接这样开两维就变成 \(O(n^2)\) 的了,所以套路地,去找找有没有什么性质,可以使得棋子或门放在哪里一定是更优的(或不是更劣的)。
首先棋子肯定要沿着欧拉序走,这个显然,所以就不会出现子树之间反复横跳的情况,所以就可以对于每棵子树单独处理了。
进一步发现,对于一棵子树,若不想把门放在根上,那么让门跟着棋子走一定不会更劣。所以门走过的路径就是整棵树删掉一些子树后剩下的部分。而若门经过的路径固定了,那么代价也就固定了,所以可以令 \(f_u\) 表示初始状态下,棋子和门都在节点 \(u\) 上,把子树 \(u\) 全部染黑所需要的最小代价。
观察发现,结束状态不一定要和初始状态相同,因为在染黑整棵树之后,就没必要再回到根节点了,不过同时此时我们也不再关心棋子和门的具体位置了。
所以要加一维 \(0/1\) 表示最后是否回到根节点。
有了状态之后,转移随便推推就有了。
换根也是容易的。在和子树有关(区分具体哪棵子树)的部分维护一个不和最值在同一子树内的最值即可(或者叫次大 / 小值),这个是常用套路了。
不过实际上维护的东西是比较多的,有点麻烦。
一点技巧:在从 \(u\) 向 \(v\) 转移的时候,若有影响,可以先把 \(u\) 的 dp 值中包含 \(v\) 的那部分扣去,然后 \(u\) 就可以当作 \(v\) 的正常子树来处理了。最后再把 \(u\) 的 dp 值回滚回来。
注意在换根 dp 中,用到父节点 \(u\) 的 dp 值一定是换根后的,也就是大写字母。
对于次大值这个东西,可以直接开个结构体来维护,每次更新就是一次 insert 操作,这样会方便一些。
struct state
{
int x1,p1,x2,p2; // x1,p1 最大值及其位置 ; x2,p2 次大值及其位置
state():x1(0),p1(-1),x2(0),p2(-1){}
il void ins(int x3,int p3){x3>=x1?(x2=x1,p2=p1,x1=x3,p1=p3):(x3>=x2&&(x2=x3,p2=p3));}
};
天依宝宝可爱!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号