ucOSII操作系统就绪表分析
在ucOSII的绪表中使用一个很妙的查找方式,下面对其查找过程进行详细分析(目的就是加快查找速度)
对于ucOSII而言,其最大的任务数是64个,因此为了标记其任务的状态,ucOSII使用了八个变量表示每个任务的状态,每个变量每个位对应任务的状态:

如果我们直接去查找就绪任务的最高优先级任务,那我们需要遍历这八个变量,去判断最高位是1,很显然在最坏情况下需要遍历64次,那有没有更好的方法呢,仔细观察发现一个规律,当任务优先级是8的时候,其就绪标志位在OSRdyTbl[1]中的第0位,8对应的二进制是00001000,这样00001正好是1,000正好是0,我们在看看其他是不是这样,例如7的二进制00000111,00000对应的是0,也就是OSRdy[0],111对应7,也就是第7位,继续验证发现确实所有的优先级都满足这个规律,因此我们可以利用这一点来加快查找速度。这样我们就有如下结构:
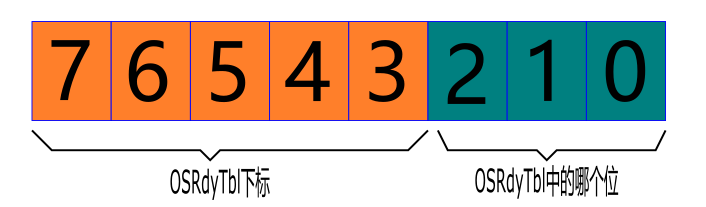
实际上有OSRdyl的下标表示中只有3,4,5三位有效,因为这里只有8组,不过这个无所谓,都是一样的。为了表示这些组中有没有就绪任务,ucOSII中定义了一个OSRdyGrp这个变量,该变量是一个8位的无符号整型,这样每一位表示每个组有无就绪任务:
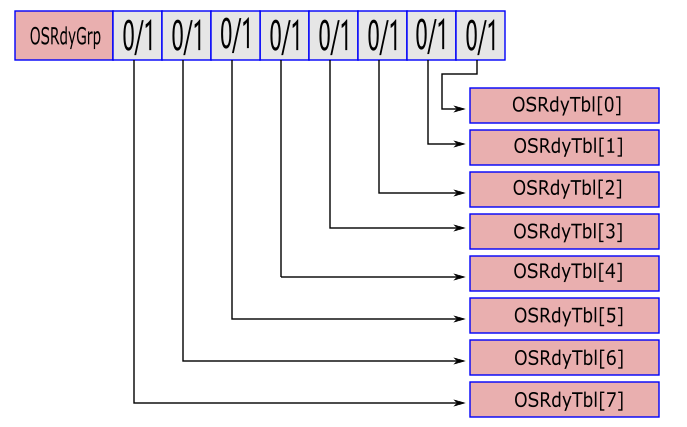
这样OSRdyGrp的初始值为0,当有一个任务创建时,那就将该任务所在的组(即OSRdyTbl)对应的OSRdyGrp相应的位设置为1,当有任务删除时,那就将该任务所在的组对应的OSRdyGrp相应的位设置为0,如下:
创建任务(登记):
OSRdyTbl[prio>>3] |= (prio&0x07);
OSRdyGrp |= (prio>>3);
删除任务(注销):
OSRdyTbl[prio>>3] &= ~(prio&0x07);
OSRdyGrp &= ~(prio>>3);
在ucOSII中为了加快速度,定义了一个数组const UINT8 OSMapTbl[8](说明:这里可以看到OSRdyGrp对其一个变量位操作会通过很多指令完成,但是如果对一个固定的常量进行位操作就减少很多指令)
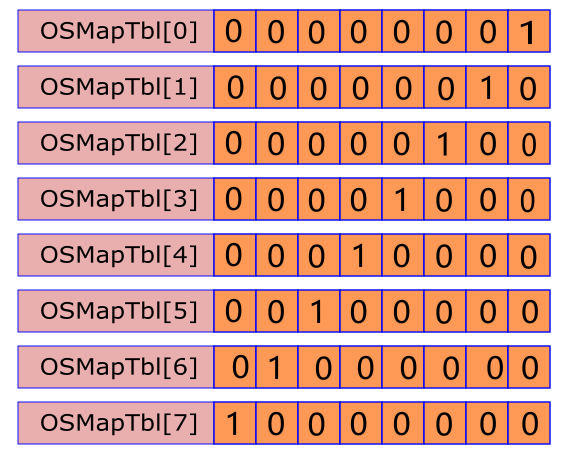
这样上面的操作就变为了如下操作:
创建任务(登记):
OSRdyTbl[prio>>3] |= OSMapTbl [prio&0x07];
OSRdyGrp |= OSMapTbl [(prio>>3)];
删除任务(注销):
OSRdyTbl[prio>>3] &= ~OSMapTbl [prio&0x07];
OSRdyGrp &= ~OSMapTbl [(prio>>3)];
这样就完成了任务创建和删除时对就绪表的操作,在ucOSII中还需要涉及到最高优先级查找,因为当当前运行任务进入阻塞态时,下一个运行任务就应该时最高优先级任务,因此我们必须找到最高优先级的任务,显然,我们需要找到数组中OSRdyTbl的为1的最高位在哪。最然这个过程很简单,但是我们需要加快查找速度,在ucOSII中定义了一个查找表,这个表可以直接索引到对应的为1的最高位(也就是就绪表中最高优先级),其实这个过程和上面对OSRdyGrp的操作是一个反过程,首先我们要确定哪个组(OSRdyTbl[8])中有就绪任务,那这个如何做呢?假设此时OSRdyGrp=5(00000101),可以看到最高优先级的组在2组(最高位为2位),现在我们还需要确定组中的哪个位,那又如何确定呢?上面说过了,需要定义一个查找表,这样我们就从这个方面下手。
首先我们需要完成OSRdyGrp=5映射到2类似这种映射(其实就是找出OSRdyGrp的最高位),其次就是找出OSRdyTb[]中的最高位,有趣的事情出现了,这两个过程其实是同一个过程,都是找一个变量的最高位,因此我们只需要设计一张表就可以完成此工作哦,这个就是ucOSII中查找就绪任务的妙处所在。好了,下面我们来设计这张表:
再次强调查找表的目的是找到一个变量最高位,比如5的最高位是2,3的最高位是1,1的最高位是0.....
最直接的办法是枚举,你没有看错,就是这么简单粗暴,总共有2的8次方就是256种情况,天啊,这我弄不了,这辈子都弄不了,其实不用你一个一个去枚举,数学家说:不就是找出一个最高位么,简单,log2X就这么easy!,好了,我们就可到了查找表:
UnMapTbl[256]={0,log21,log22,log23,log24,log25,log26,log27......};
通过excel计算得到UnMapTbl[256]={ 0,0,1,2,2,2,3,3,3......};
马上有人开始说了,这不对吧,这个和源码中的不一样,确实,别急,且听我说,这里由于ucOSII中的优先级是反的,也就是数值越大,其优先级越低,因此,我们不是找到最高位,而是找到最低位,这样查找表就变成了源码中的那样了,也就是
INT8U const OSUnMapTbl[256] = { 0, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x00 to 0x0F */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x10 to 0x1F */ 5, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x20 to 0x2F */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x30 to 0x3F */ 6, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x40 to 0x4F */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x50 to 0x5F */ 5, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x60 to 0x6F */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x70 to 0x7F */ 7, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x80 to 0x8F */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0x90 to 0x9F */ 5, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0xA0 to 0xAF */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0xB0 to 0xBF */ 6, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0xC0 to 0xCF */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0xD0 to 0xDF */ 5, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0, /* 0xE0 to 0xEF */ 4, 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, 0, 1, 0 /* 0xF0 to 0xFF */ };
确定最高优先级的过程就是这样:
grp = OSUnMapTbl [OSRdyGrp];
prio = (grp <<3) + OSUnMapTbl [OSRdyTbl [grp] ;
至此,整个ucOSII的就绪表的分析结束了,思想很重要,不要仅仅拘泥据源码。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号