[数学]卡特兰数

前言

咕比赛写博客的我。哭哭。
在本篇文章的剩余部分中，我们定义$C(n)$为卡特兰数的第$n$项

定义

翻阅了一堆文章，也没找到真正的定义，暂且拿这个充当定义:
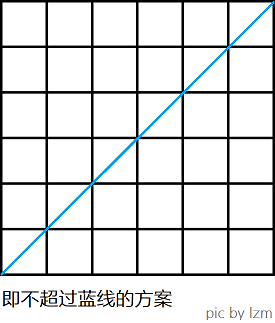
$C(n)$表示，从原点出发，每次向x或y轴正方向移动1单位，到达点(n,n)，且在移动过程中不越过第一象限平分线的移动方案数。

通项公式

我们记$C(n)$为卡特兰数的第$n$项

$$C(n)= \left( \begin{matrix}2n \\ n\end{matrix} \right) - \left( \begin{matrix}2n \\ n + 1\end{matrix} \right)$$

证明

首先根据组合数学，我们知道如果不考虑第一象限平分线的限制，方案数为$\left(\begin{matrix}2n \\ n\end{matrix}\right)$。
注意到任何一种非法的方案，都至少有一个点$p$碰到了直线$y=x+1$，那么我们将这条路径在$p$点以上的在直线$y=x+1$以下的部分沿直线$y=x+1$镜像到直线$y=x+1$上。
看图理解:上图中的绿线为$y=x+1$，红线为原非法路径在$p$上的部分，蓝线为镜像后的结果。
我们会发现任何一种非法方案都可以变换成(0,0)到(n-1,n+1)的一条路径，且存在一一映射关系，所以总方案数为:$\left(\begin{matrix}2n \\ n\end{matrix}\right)-\left(\begin{matrix}2n \\ n+1\end{matrix}\right)$

化简

$$C(n)=\left(\begin{matrix}2n \\ n\end{matrix}\right)-\left(\begin{matrix}2n \\ n+1\end{matrix}\right)$$

$$=\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n+1)!(n-1)!}$$

$$=\frac{1}{n+1}(\frac{(2n)!(n+1)}{n!n!}-\frac{(2n)!}{n!(n-1)!})$$

$$=\frac{1}{n+1}(\frac{(2n)!(n+1)}{n!n!}-\frac{(2n)!\times n}{n!n!})$$

$$=\frac{1}{n+1}\frac{(2n)!(n+1)-(2n)! \times n}{n!n!}$$

$$=\frac{1}{n+1}\frac{(2n)!}{n!n!}$$

$$=\frac{1}{n+1}\left(\begin{matrix}2n \\ n\end{matrix}\right)$$

变形

$$C(n)=\frac{1}{n+1}\sum_{i=0}^n\left(\begin{matrix}n \\ i \end{matrix}\right)^2$$

递推

$$C(n+1)=\sum_{i=0}^nC(i)C(n-i),\ C(0)=1$$

$$C(n+1)=\frac{2(2n+1)}{n+2}C(n),\ C(0)=1$$

应用

1. n对括号的合法配对方案书
2. n个节点的二叉树的形态数
3. n+1个叶子(n个非叶节点)的满二叉树的形态数, 走到左儿子+1,走到 右儿子-1,类似于括号匹配(大致同2)
4. n个数入栈后出栈的排列总数
5. 对凸n+2边形进行不同的三角形分割的方案数(分割线断点仅为顶点，且分割线仅在顶点上相交)
6. n层的阶梯切割为n个矩形的切法数

卡特兰数与OI初赛

首先背诵上述应用场景，然后记忆卡特兰数的前几项:1,1,2,5,14,42,132。

拓展

$n+m$个人排队买票，并且满足$n \geq m$，票价为50元，其中n个人有且仅有一张$50$元钞票，m个人有且仅有一张$100$元钞票，初始时候售票窗口没有钱，问有多少种排队的情况数能够让大家都买到票。
如果$n=m$可以直接用Catalan数解决，也就是将有50元的人看成是上述应用中的左括号，有100元的人看成是右括号。
对与$n>m$的情况，假设所有人都可以买到票的情况数是$A_{n,m}$，不能让每个人都买到的情况数是$B_{n,m}$，设最早买不到票的人为$p$，他一定手持100元且售票处没有50元，那么这时将前p个人的钱从50元变成100元，从100元变成50元(不考虑顺序，所以没有影响)，这时候就有$n+1$个人有50元，$m-1$个有100元的，所以就得到$B_{n,m}=\left(\begin{matrix}n+m \\ n+1\end{matrix}\right)$，那么$A_{n,m}=\left(\begin{matrix}n+m \\ n\end{matrix}\right)-\left(\begin{matrix}n+m \\ n+1\end{matrix}\right)$。
这正是应用了上文证明的"翻折"思想。