Machine Learning 03 最小二乘法、极大似然法、交叉熵

损失函数

神经网络里的标准和人脑标准相比较 相差多少的定量表达。

最小二乘法

首先要搞明白两个概率模型是怎么比较的。有三种思路，最小二乘法、极大似然估计，交叉熵

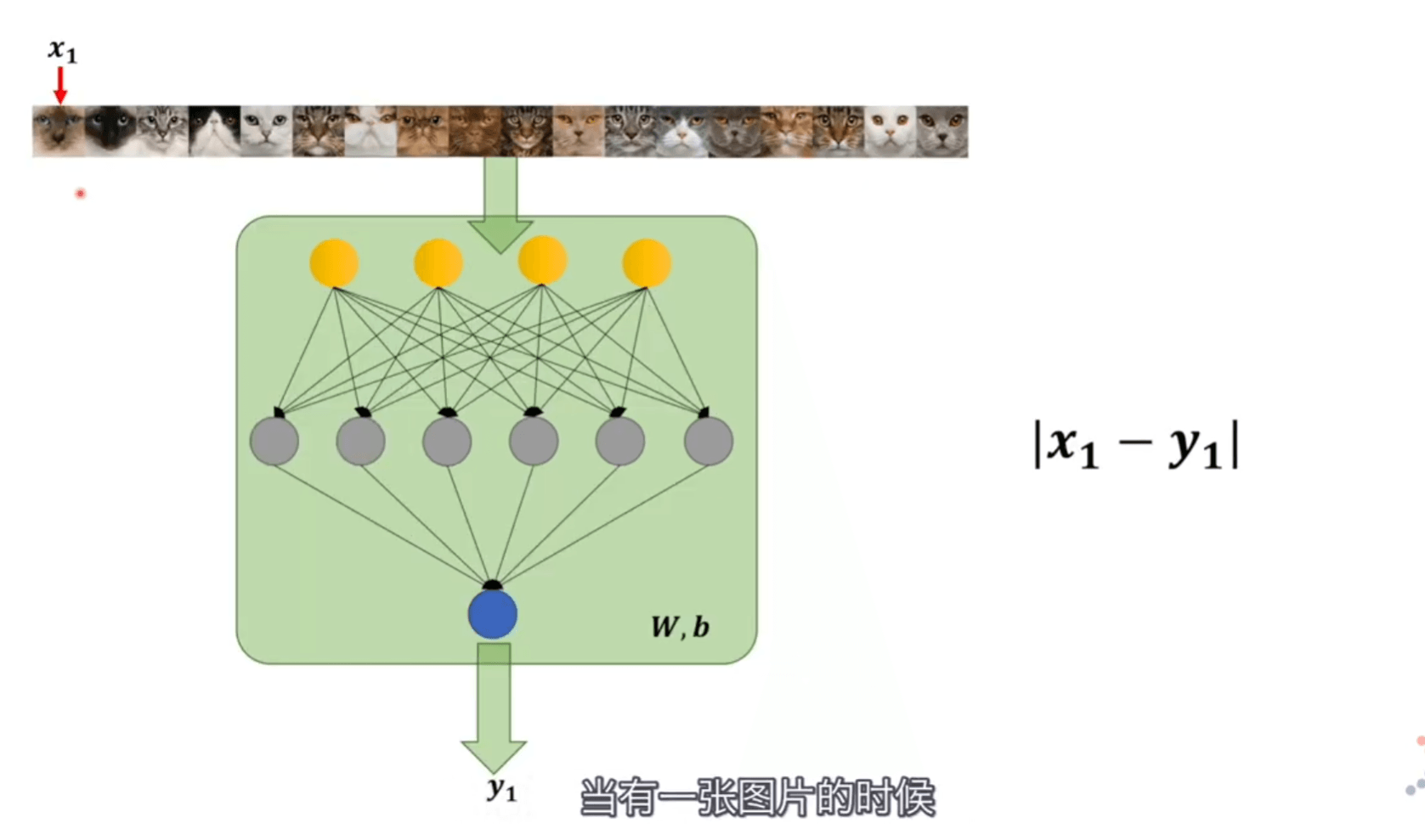
当一张图片人脑判断的结果是 $x1$，神经网络判断的结果是 $y1$，直接把它们相减 $\left|x_{1}-y_{1}\right|$ 就是他们相差的范围。我们将多张图片都拿过来判断加起来，当最终值最小的时候，$\min \sum_{i=1}^{n}\left|x_{i}-y_{i}\right|$ 就可以认定两个模型近似。

但是绝对值在定义域内不是全程可导的，所以可以求平方 $\min \sum_{i=1}^{n}\left(x_{i}-y_{i}\right)^{2}$

就这是最小二乘法，但是只用它判断两个概率模型差别有多少，去作为损失函数会比较困难。所以引入极大似然估计

极大似然估计

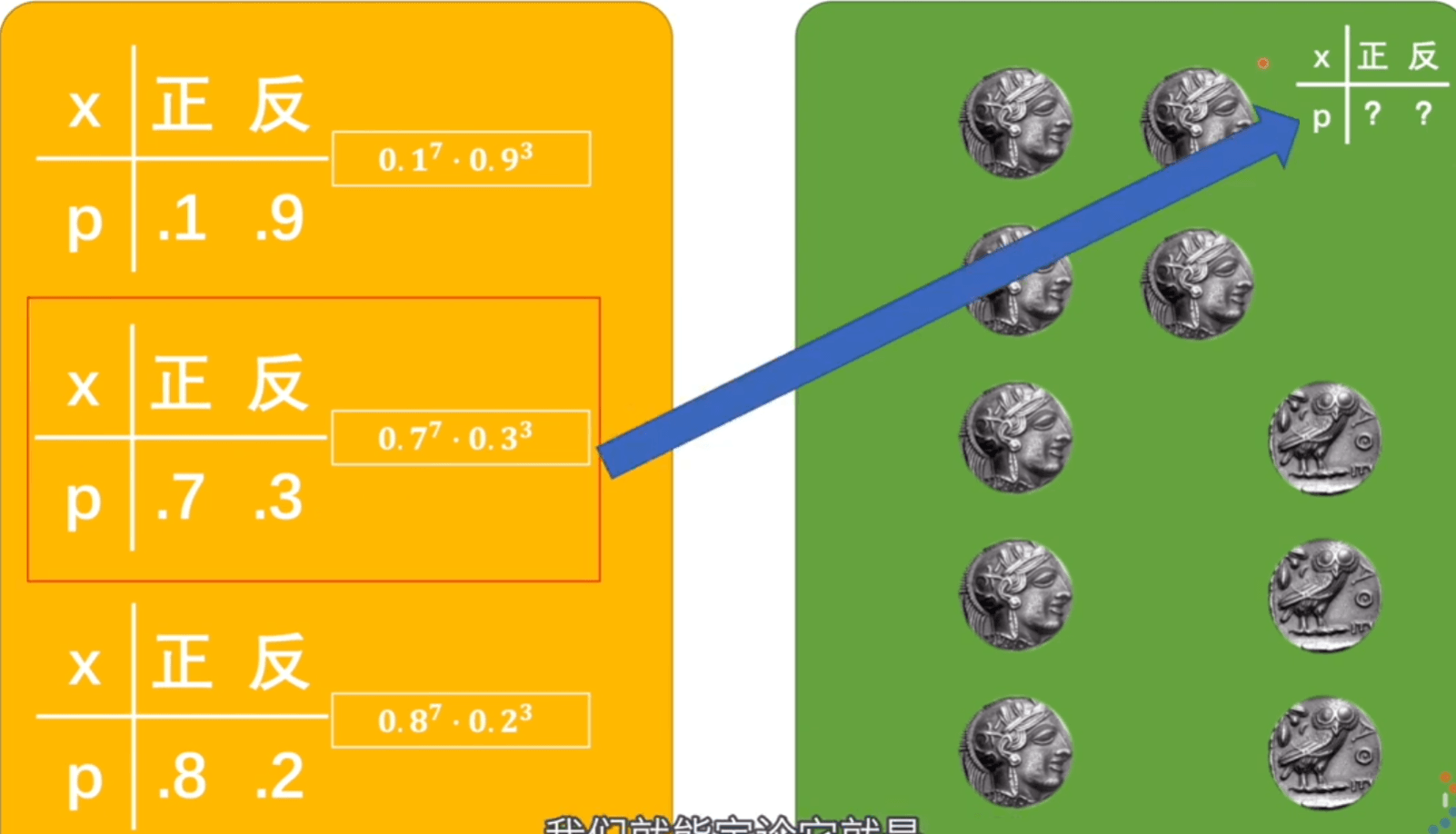
似然值是真实的情况已经发生，我们假设它有很多模型，在这个概率模型下，发生这种情况的可能性就叫似然值。

挑出似然值最大的，那可能性也就越高，此时的概率模型应该是与标准模型最接近的。

$$\begin{array}{l} P\left(C_{1}, C_{2}, C_{3}, \ldots, C_{10} \mid \theta\right) \\ P\left(x_{1}, x_{2}, x_{3}, x_{4}, \ldots, x_{n} \mid W, b\right) \end{array}$$

$\theta$ 是抛硬币的概率模型，$W,b$ 是神经网络的概率模型。前者结果是硬币是正还是反，后者结果是图片到底是不是猫。

$$\begin{array}{l} P\left(x_{1}, x_{2}, x_{3}, x_{4}, \ldots, x_{n} \mid W, b\right) \\ =\prod_{i=1}^{n} P\left(x_{i} \mid W, b\right) \end{array}$$

在神经网络是这样的参数下，输入的照片如果是猫概率是多少、如果不是猫概率是多少，所有图片判断后，相乘得到的值就是似然值。取到极大似然值就是最接近的值。

但在训练的时候 $W、b$ 无论输入什么样的照片都是固定的值，如果我们都用猫的照片来确定的话标签都是$1$，那就没有办法进行训练，理论可行却没有操作性。但是我们还可以利用条件，训练神经网络的时候既可以得到 $x_{i}$ 也可以得到 $y_{i}$， $y_{i}$ 的输出结果依赖 $W,b$ 。每次输入照片不一样，$y_{i}$ 的结果也就不一样。

$$\begin{array}{l} =\prod_{i=1}^{n} P\left(x_{i} \mid W, b\right) \\ =\prod_{i=1}^{n} P\left(x_{i} \mid y_{i}\right) \end{array}$$

$x_{i}$ 的取值是 $0、1$ ，符合二项伯努利分布，概率分布表达式为

$$f(x)=p^{x}(1-p)^{1-x}=\left\{\begin{array}{ll} p, & x=1 \\ 1-p, & x=0 \end{array}\right.$$

$x=1$ 就是图片为猫的概率。而 $p$ 就是 $y_{i}$ (神经网络认定是猫的概率)，将其带入替换 $P\left(x_{i} \mid y_{i}\right)$

$$=\prod_{i=1}^{n} y_{i}^{x_{i}}\left(1-y_{i}\right)^{1-x_{i}}$$

我们更喜欢连加，在前面加 $log$ ，并化简

$$\begin{array}{l} \log \left(\prod_{i=1}^{n} y_{i}^{x_{i}}\left(1-y_{i}\right)^{1-x_{i}}\right) \\ =\sum_{i=1}^{n} \log \left(y_{i}^{x_{i}}\left(1-y_{i}\right)^{1-x_{i}}\right) \\ =\sum_{i=1}^{n}\left(x_{i} \cdot \log y_{i}+\left(1-x_{i}\right) \cdot \log \left(1-y_{i}\right)\right) \end{array}$$

所以，求极大似然值，就是求如下公式

$$\begin{array}{l} \max \left(\sum_{i=1}^{n}\left(x_{i} \cdot \log y_{i}+\left(1-x_{i}\right) \cdot \log \left(1-y_{i}\right)\right)\right) \\ \min -\left(\sum_{i=1}^{n}\left(x_{i} \cdot \log y_{i}+\left(1-x_{i}\right) \cdot \log \left(1-y_{i}\right)\right)\right) \end{array}$$

复习一下对数

1. $\log _{a}(1)=0$
2. $\log _{a}(a)=1$
3. $负数与零无对数$
4. $\log _{a} b * \log _{b} a=1$
5. $\log _{a}(M N)=\log _{a} M+\log _{a} N$
6. $\log _{a}(M / N)=\log _{a} M-\log _{a} N$
7. $\log _{a} M^{n}=n \log _{a} M(\mathrm{M}, \mathrm{N} \in \mathrm{R})$
8. $\log _{a^{n}} M=\frac{1}{n} \log _{a} M$
9. $a^{\log _{a} b}=b$

交叉熵

要想直接比较两个模型，前提是两个模型类型是同一种，否则就不能公度。概率模型如果想要被统一衡量，我们需要引入熵（一个系统里的混乱程度）。

信息量

我们想获取信息量的函数，就要进行定义。并找寻能让体系自洽的公式。

$${f}({x}):=\text { 信息量 }\\ {f}( 阿根廷夺冠 )={f}( 阿根廷进决赛 )+{f}( 阿根廷赢了决赛 ) \\ f\left(\frac{1}{8}\right)=f\left(\frac{1}{4}\right)+f\left(\frac{1}{2}\right)\\ P(\text { 阿根廷夺冠 })=P(\text { 阿根廷进决赛 }) \cdot {P} \text { (阿根廷赢了决赛 })\\ $$

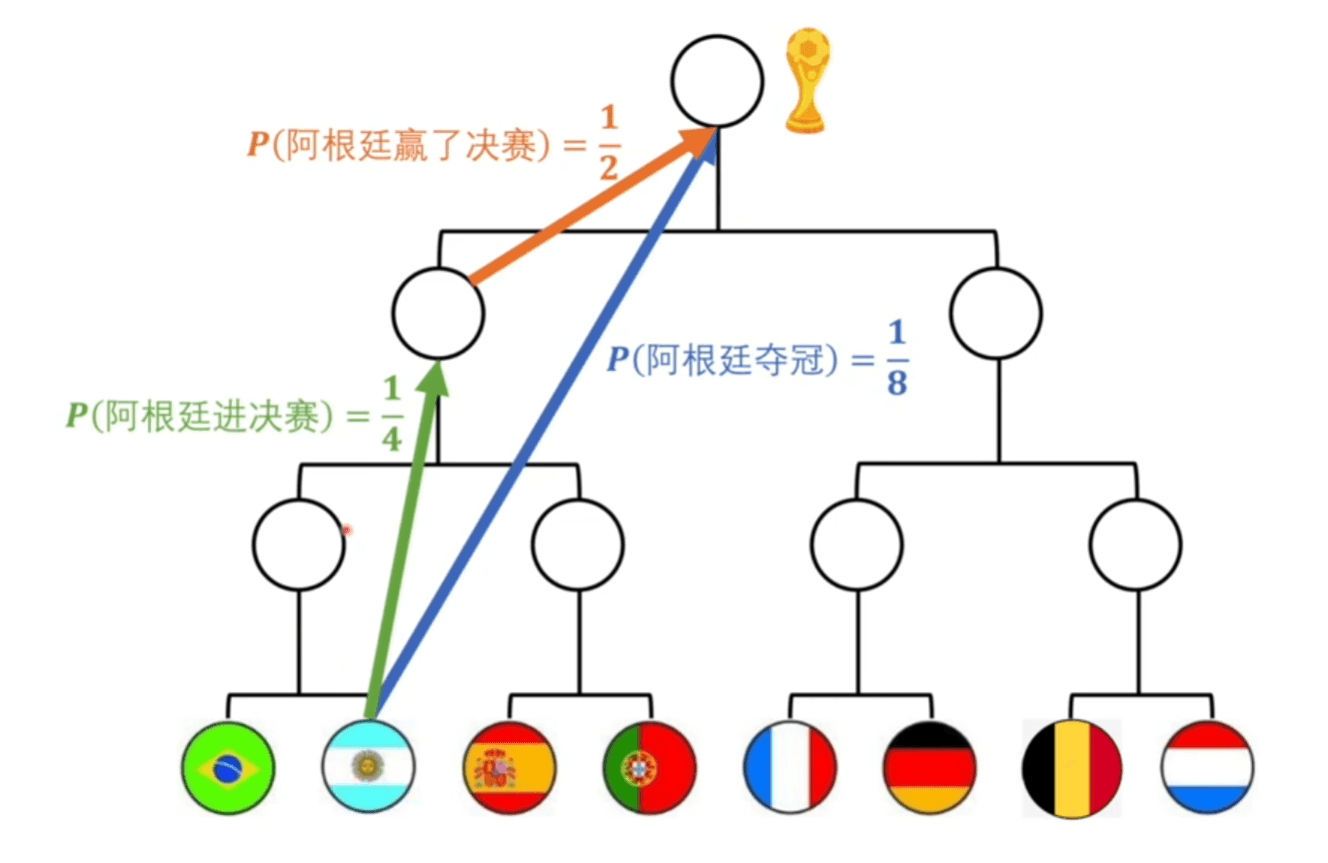
将上面的第四条公式带入第三条得到如下第二条。为了使信息量定义能让体系自洽，我们给定定义 $log$，这样符合相乘变相加的形式。

$$\begin{array}{c} f(x):=? \log _{?} x \\ f\left(x_{1} \cdot x_{2}\right)=f\left(x_{1}\right)+f\left(x_{2}\right) \end{array}$$

为了符合我们最直观的感觉，因为概率越小，信息量越大。而 $log$ 函数单调递增，我们转换方向。

$$\begin{array}{c} f(x):=-\log _{2} x \\ f\left(x_{1} \cdot x_{2}\right)=f\left(x_{1}\right)+f\left(x_{2}\right) \end{array}$$

看计算机里多少位数据，给计算机输入一个16位数据，输入之前随便取的值是 $1/2^{16}$ 的概率 ，输入之后的概率直接变为了 $1$ 。信息量就是 $16$ 比特。

信息量可以理解为一个事件从原来不确定到确定它的难度有多大，信息量大，难度高。

熵不是衡量某个具体事件，而是整个系统的事件，一个系统的从不确定到确定难度有多大

它们都是衡量难度，单位也可以一样都是比特。

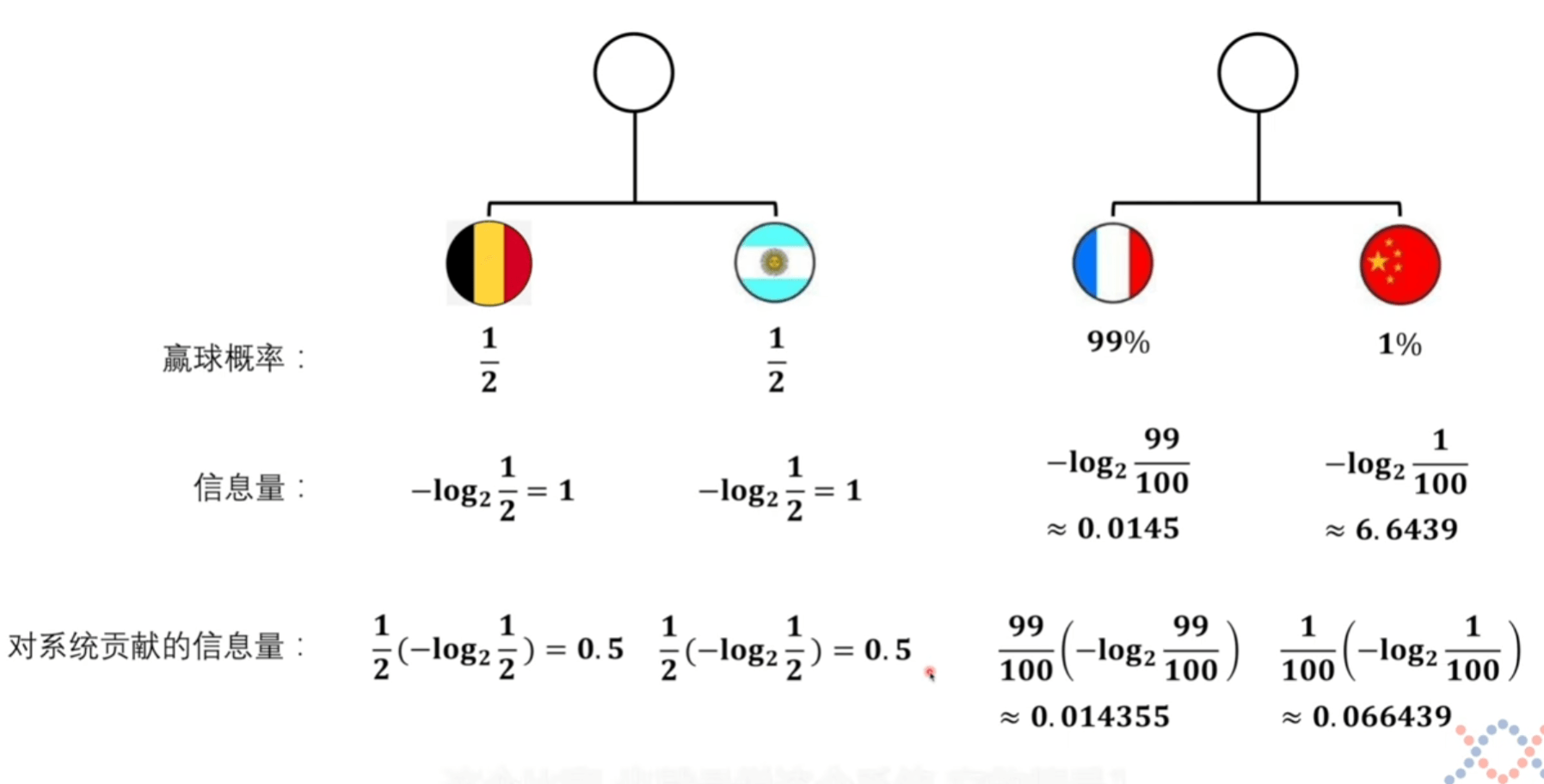
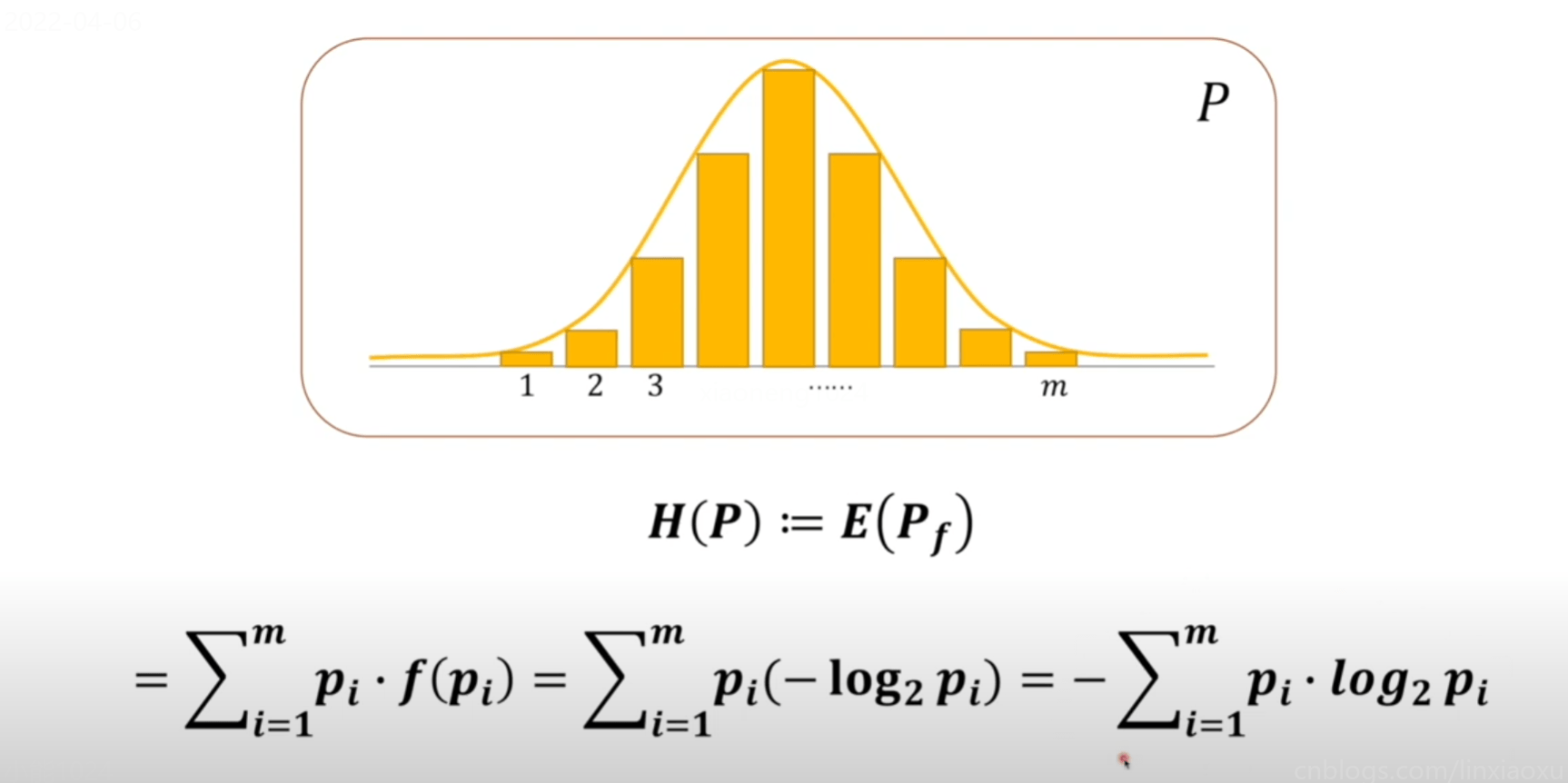
系统熵的定义

将上方对系统贡献的信息量可以看成是期望的计算。

KL散度

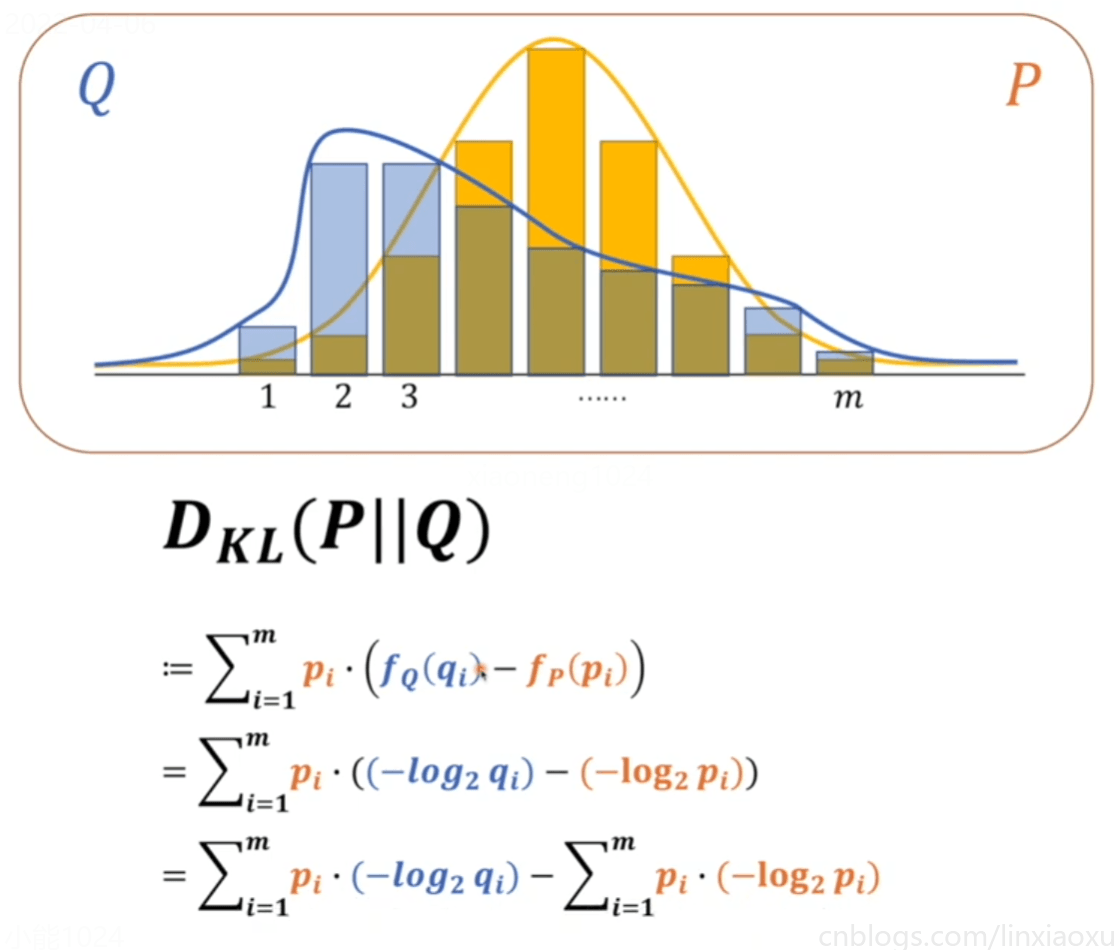
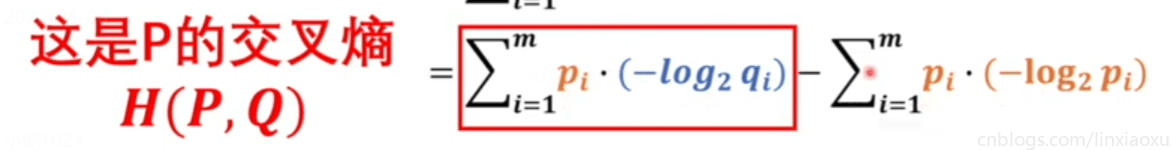
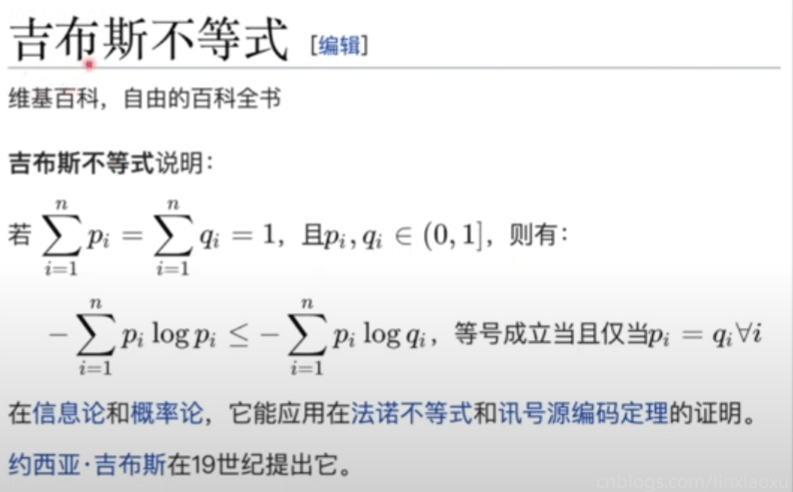
KL散度绝对是大于等于$0$的，当$Q、P$相等的时候等于$0$，不相等的时候一定大于$0$

为了让$Q、P$两个模型接近，所以必须使交叉熵最小

交叉熵中 $m$ 是两个概率模型里事件更多的那个，换成 $n$ 是图片数量。

对$m$选择的解释：假如$p$的事件数量是$m$，$q$的事件数量是$n$，$m＞n$，那么写成$∑$求和，用较大的$m$做上标。就可以分解为，$∑1到n+∑n+1到m$，那么对于$q$来说，因为$q$的数量只有$n$，那么对应的$q$的部分$∑n+1到m$都等于$0$。

$$\begin{array}{l} \boldsymbol{H}(\boldsymbol{P}, \boldsymbol{Q}) \\ =\sum_{i=1}^{m} p_{i} \cdot\left(-\log _{2} q_{i}\right) \\ =\sum_{i=1}^{n} x_{i} \cdot\left(-\log _{2} q_{i}\right) \\ =-\sum_{i=1}^{n}\left(x_{i} \cdot \log _{2} y_{i}+\left(1-x_{i}\right) \cdot \log _{2}\left(1-y_{i}\right)\right) \end{array}$$

$P$ 是基准，要被比较的概率模型，我们要比较的人脑模型，要么完全是猫要么不是猫。

$x_{i}$ 有两种情况，而 $y_{i}$ 只判断图片有多像猫，并没有去判断相反的这个猫有多不像猫，而公式里的 $x_{i}$ 与 $q_{i}$ 要对应起来，当 $x_{i}$ 为 $1$ ，要判断多像猫，当 $x_{i}$ 为 $0$ 的时候，要判断不像猫的概率。

最后我们推导出来，公式跟极大似然推导出来的是一样的。但是从物理角度去看两者是有很大不同的，只是形式上的一样。

• 极大似然法里的 $log$ 使我们按习惯引入的，把连乘换成相加。而交叉熵的 $log$ 是写在信息量定义里的，以 $2$ 为底，计算出来的单位是比特，是有量纲的。
• 极大似然法求的是最大值，我们按习惯求最小值。而交叉熵负号是写在定义里的。