玩转二叉树

玩转二叉树

---

一、目的

-掌握vector用法
-掌握二叉树的创建
-掌握二叉树的镜像翻转
-掌握二叉树的层序输出
-掌握队列的用法

二、实验内容与设计思想

玩转二叉树

给定一棵二叉树的中序遍历和前序遍历，请你先将树做个镜面反转，再输出反转后的层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。

输入格式：
输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。

输出格式：
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

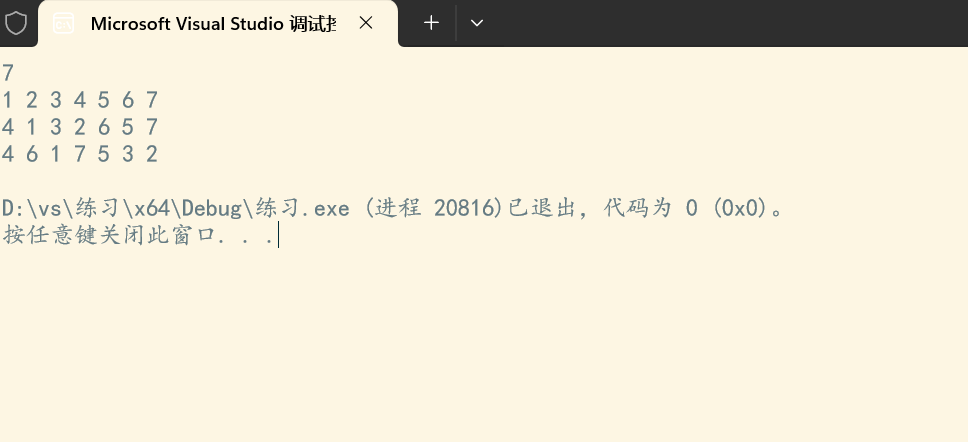
输入样例：
7
1 2 3 4 5 6 7
4 1 3 2 6 5 7
输出样例：
4 6 1 7 5 3 2
函数相关伪代码

1.动态数组n1,n2来储存二叉树的中序遍历和前序遍历的值
2.定义树的结构
3.递归创建二叉树
4.递归反转二叉树
5.队列存储，层序输出

函数代码

#include<iostream>
#include<vector>
#include <queue>
using namespace std;
struct BiNode {
    int k;
    struct BiNode* rchild;
    struct BiNode* lchild;
};
BiNode* Create(int k)
{
	BiNode* node = new BiNode;
	node->k = k;
	node->lchild = NULL;
	node->rchild = NULL;
	return node;
}
BiNode* buildTree(vector<int>& n1, vector<int>& n2, int i,int a,int &p) {
	 int m;
	 if (i > a) {
		return NULL;
	}
	 BiNode* node = Create(n2[p++]);
	 if (i == a) {
		 return node;
	 }
		for (m = i;m <= a;m++) {
			if (n1[m] == node->k) {
				break;
			}
		}
		node->lchild = buildTree(n1,n2,i,m-1,p);
		node->rchild = buildTree(n1,n2, m + 1,a,p);
		return node;
}
void Mirrortree(BiNode* root) {
	if (root == NULL) {
		return;
	}
	swap(root->lchild, root->rchild);
	Mirrortree(root->lchild);
	Mirrortree(root->rchild);
}
void Showtree(BiNode* node) {
	if (node == NULL) {
		return;
	}
	queue<BiNode*> q;
	q.push(node);
	int f = 1;
	while (!q.empty()) {
		BiNode* current = q.front();
		q.pop();
		if (f!=1) {
			cout << " ";
		}
		cout << current->k;
		f = 0;
		if (current->lchild != NULL) {
			q.push(current->lchild);
		}
		if (current->rchild != NULL) {
			q.push(current->rchild);
		}
	}
	cout << endl;
}
int main()
{
	int a, i,p=0;
	cin >> a;
	vector<int> n1(a), n2(a);
	for (int i = 0; i < a; i++)
	{
		cin >> n1[i];
	}
	for (int i = 0; i < a; i++)
	{
		cin >> n2[i];
	}
	BiNode* root = buildTree(n1, n2, 0, a - 1,p);
	Mirrortree(root);
	Showtree(root);
	return 0;
}

三、实验使用环境

以下请根据实际情况编写

• 操作系统：Windows 11专业版
• 编程语言：C++
• 开发工具：[Visual Studio 2022]

---

四、实验步骤和调试过程

玩转二叉树

本机运行截图

---

五、实验小结

遇到的问题及解决方法：

1. 问题：创建的树未正确处理

• 解决方法：优化代码，修改递归创建树的方法

实验体会和收获：

这段代码实现了一个二叉树的构建、镜像以及层序遍历显示。首先，先自定义一个树的结构，然后通过Create函数来创建单个节点。在此时传递一个值，来构建此节点。之后，用n1和n2来存储先序遍历与中序遍历的结果，之后buildTree函数利用先序遍历序列n1和中序遍历序列n2来重建二叉树，其中使用循环来判断父节点位置，i和a表示当前子树在n1中的起始和终止位置，即左右孩子在中序遍历的起始节点和中止节点。p用于追踪n2中的位置，使用递归实现树的创建。Mirrortree函数实现二叉树的镜像，即用递归来交换每个节点的左右子树。Showtree函数以层序遍历的方式显示二叉树，使用队列来实现，队列依照顺序来存储节点值，并在此期间不断入队和出队来展示层序便利的值，当遇到一个输出节点，就出队，判断一下左右孩子是否存在，并存储其节点的左孩子和右孩子，直到队列为空，表示树的节点都已输出。最后，在main函数中，读取节点数量和两个遍历序列，构建二叉树，返回根节点，使用根结点，进行镜像操作，并显示结果。