排座位-效率分析
排座位-效率分析
一、目的
-掌握时间复杂度
-掌握方法来降低运行时间
-掌握弗洛伊德算法
二、实验内容与设计思想
排座位
布置宴席最微妙的事情,就是给前来参宴的各位宾客安排座位。无论如何,总不能把两个死对头排到同一张宴会桌旁!这个艰巨任务现在就交给你,对任何一对客人,请编写程序告诉主人他们是否能被安排同席。
输入格式:
输入第一行给出3个正整数:N(≤100),即前来参宴的宾客总人数,则这些人从1到N编号;M为已知两两宾客之间的关系数;K为查询的条数。随后M行,每行给出一对宾客之间的关系,格式为:宾客1 宾客2 关系,其中关系为1表示是朋友,-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行,每行给出一对需要查询的宾客编号。
这里假设朋友的朋友也是朋友。但敌人的敌人并不一定就是朋友,朋友的敌人也不一定是敌人。只有单纯直接的敌对关系才是绝对不能同席的。
输出格式:
对每个查询输出一行结果:如果两位宾客之间是朋友,且没有敌对关系,则输出No problem;如果他们之间并不是朋友,但也不敌对,则输出OK;如果他们之间有敌对,然而也有共同的朋友,则输出OK but...;如果他们之间只有敌对关系,则输出No way。
输入样例:
7 8 4
5 6 1
2 7 -1
1 3 1
3 4 1
6 7 -1
1 2 1
1 4 1
2 3 -1
3 4
5 7
2 3
7 2
输出样例:
No problem
OK
OK but...
No way
函数相关伪代码
1.数组a[N+1][N+1],s[N+1][N+1]
2.输入个数x,y,z,z都在a里,s要z为1时输入
3.循环输入数组值
4.找共同好友使s[i][j]=1
5.判断输出
函数代码
1.c++实现
#include<iostream>
using namespace std;
int main() {
int N,M,K,x,y,z;
cin>>N >>M >>K;
int s[N+1][N+1]={0}, a[N+1][N+1]={0};
for(int i = 0; i<M; i++) {
cin>>x>>y>>z;
s[x][y]=z;
s[y][x]=z;
if(z==1){
a[x][y]=1;
a[y][x]=1;
}
}
for(int k=1;k<=N;k++){
for(int i=1;i<=N;i++){
for(int j=1;j<=N;j++){
if(a[i][k]==1&&a[k][j]==1){
a[i][j]=1;
}
}
}
}
while(K--) {
int l, m;
cin >> l >> m;
if(s[l][m] == 1) {
cout << "No problem" << endl;
} else if(s[l][m]==0){
if(a[l][m]==0){
cout << "OK" << endl;
} else {
cout<<"No problem"<<endl;
}
} else if(s[l][m] == -1) {
if(a[l][m] == 1) {
cout << "OK but..."<<endl;
} else {
cout<<"No way"<<endl;
}
}
}
return 0;
}
2.c实现(效率低)
#include<stdio.h>
int main()
{
int N,i,y,k,u,l,M,K,j;
scanf("%d %d %d",&N,&M,&K);
int a[M][3];
int m[K],n[K];
for(i=0;i<M;i++){
scanf("%d %d %d",&a[i][0],&a[i][1],&a[i][2]);
}
for(i=0;i<K;i++){
scanf("%d %d",&m[i],&n[i]);
}
i=0;
while(i<K){
l=0;
y=0;
for(k=0;k<M;k++){
if(a[k][0]==m[i]&&a[k][1]==n[i]||a[k][1]==m[i]&&a[k][0]==n[i]){
if(a[k][2]==-1){
for(u=0;u<M;u++){
if(m[i]==a[u][0]&&a[u][2]==1||m[i]==a[u][1]&&a[u][2]==1){
if(m[i]==a[u][0]){
l=a[u][1];
}else{
l=a[u][0];
}
}
for(j=0;j<M;j++){
if(l==a[j][1]&&a[j][0]==n[i]&&a[j][2]==1||l==a[j][0]&&a[j][1]==n[i]&&a[j][2]==1){
printf("OK but...\n");
y=1;
break;
}
}
if(y==1){
break;
}
}
if(y==0){
printf("No way\n");
y=1;
break;
}
}else if(a[k][2]==1){
printf("No problem\n");
y=1;
break;
}
}
}
if(y==0){
printf("OK\n");
}
i++;
}
return 0;
}
时间复杂度O(KMM),空间复杂度O(K+M)
三、实验使用环境
以下请根据实际情况编写
- 操作系统:Windows 11专业版
- 编程语言:C++,C
- 开发工具:[Visual studio 2022 ,DevC++]
四、实验步骤和调试过程
排座位
本机运行截图
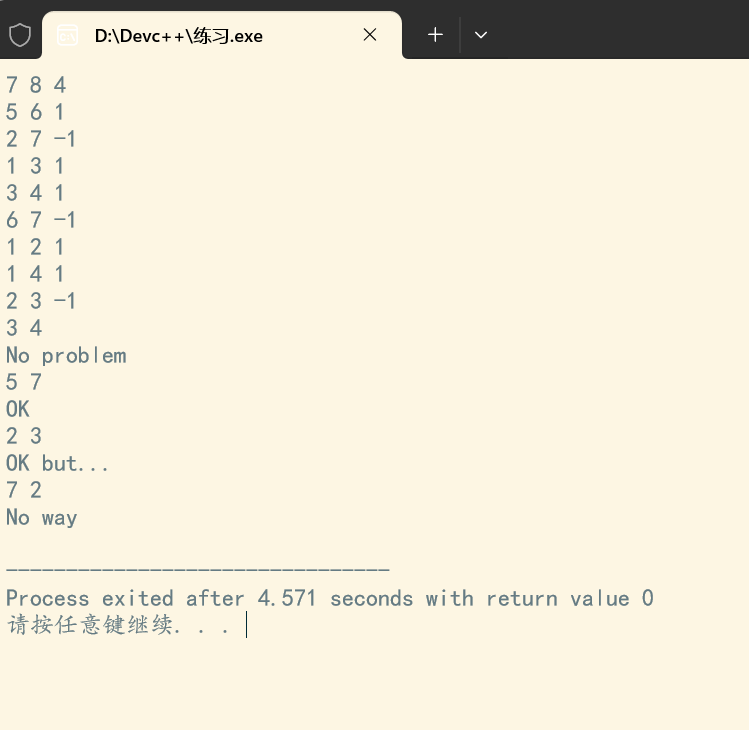
五、实验小结
遇到的问题及解决方法:
- 问题:运行超时
- 解决方法:优化代码,提高效率
实验体会和收获:
这两段代码一个是用C语言编写的,一个是用c++来写的,用于处理客人的关系问题。它们首先读取客人与客人之间关系的数值,然后根据输入的信息来判断后续查询的客人关系。
C++代码使用二维数组来储存,需要用到两个二维数组,节点的位置就是客人,数组一个是完全未处理的,就是存储题目的信息,一个数组使用弗洛伊德算法预处理所有节点中客人与客人是朋友的节点,使其节点存储为1,不是朋友的节点为0,只存储两人是朋友的节点,通过这两个数组,这使得后续的查询处理非常快速,只要输入客人就马上可以找到之间的关系。
C代码则直接存储客人的信息,并用条件语句来判断之间的关系,并且每次如果查询的客人与客人之间是敌对关系,还要在循环里面再便利两重循环,来确定两人之间是否有共同朋友,不会保留之间遍历过的结果,使时间复杂度较高,会运行超时,且要用大量的判断语句和break(使用goto也可以)语句,使代码非常复杂难懂,但空间复杂度低。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号