差分约束系统学习笔记（超详细）

一、什么是差分约束系统

差分约束系统就是让你求解一个方程组，这个方程组长这样：

\[\left\{ \begin{gather*} x_{c_1}-x_{c'_1} \le w_1\\ x_{c_2}-x_{c'_2} \le w_2\\ \vdots\\ x_{c_m}-x_{c'_m} \le w_m\\ \end{gather*} \right. \]

二、差分约束系统算法推导

观察这个方程，我们发现和最短路有点关系，因为从任意点跑最短路每条边 \(u \rightarrow v\) 一定满足 \(dis_u+w \ge dis_v\)，然后移项得到 \(dis_v \le dis_u+w\)，然后再次移项得到 \(dis_v-dis_u \le w\)，你就会发现这和方程组形式简直一模一样，只是方向变了，于是我们倒着建图跑最短路就行了。但是问题来了，如果每个点都跑最短路时间复杂度太高了吧？于是我们可以建立一个超级源点 \(0\)，然后让 \(0\) 连向每个点就行了。那如何设置这些边（\(0\) 连向每个点的这些边）的权值呢？你可能第一反应就是 \(0\)，那如果这样到每个点的最短路不就是 \(0\) 了吗？不是，只有当边权全部为正整数时到每个点的最短路才是 \(0\)，然而这也不影响，因为边权如果全是正整数将每个 \(x\) 全部设置为 \(0\) 也是满足约束条件的，然后如果边权有负数那到每个点的最短路就不一定是 \(0\) 了，还有可能是负数。

三、差分约束系统可以解决的两类基础问题

• 给你一个差分约束系统，问你 \(x_a-x_b\) 的最大/最小值。
• 给你一个差分约束系统，并且对于每个 \(x\) 都有约束条件（例如小于多少或大于多少），问你 \(\sum_{i = 1}^n x_i\) 的最大/最小值。

四、问题 \(1\) 的解法

我们先考虑最大值，我们看原本的差分约束系统已经被建成图论，因为一个最大值如果合法，就必须得满足从 \(b\) 到 \(a\) 的任意一条路径都大于等于这个最大值，那这个最大值最大不就是从 \(b\) 到 \(a\) 的最长路吗？
附个板书让大家理解一下（这里是最大值的推导，转载自我的老师shi_kan）：

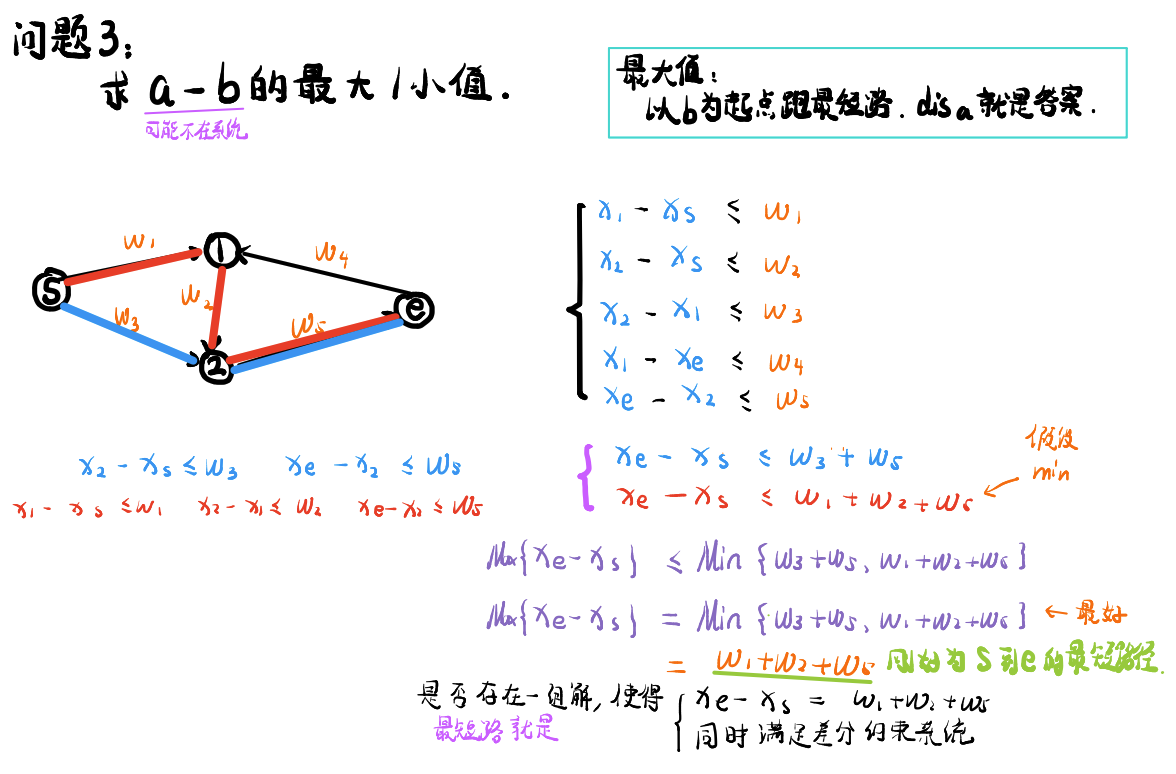
那最小值呢，我们可以尝试让建图的定义变得不同，之前是 \(u \stackrel{w}{\rightarrow} v\) 表示 \(x_v-x_u \le w\)，现在是 \(u \stackrel{w}{\rightarrow} v\) 表示 \(x_v-x_u \ge w\)，那么你就会发现可以延续最大值的推论，对于一个最小值是否合法，必须得图上满足任何一条从 \(b\) 到 \(a\) 的路径都大于等于这个最小值，那这个最小值最小不就是从 \(b\) 到 \(a\) 的最长路吗？
附个板书让大家理解一下（这里是最大值的推导，转载自我的老师shi_kan）：

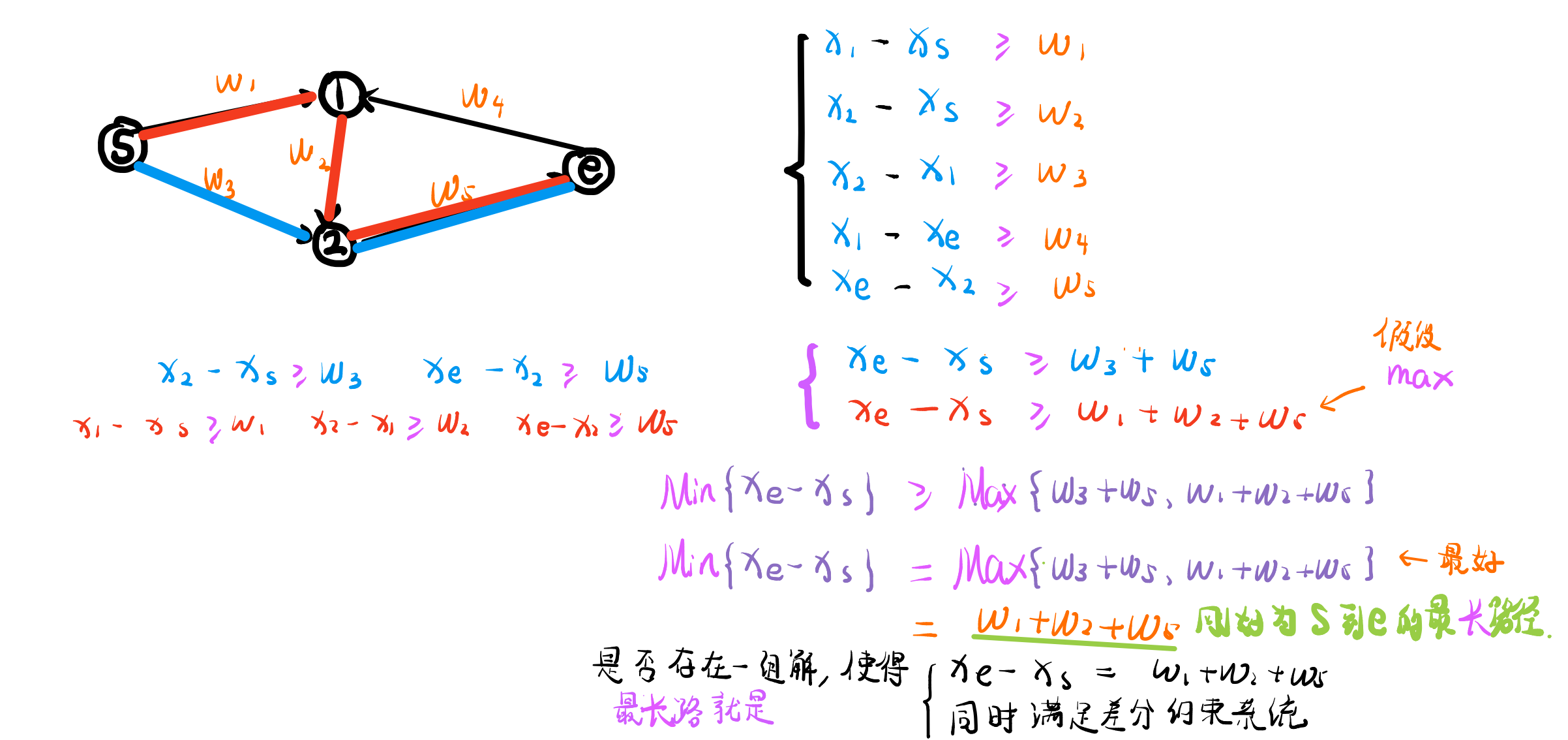
五、问题 \(2\) 的解法

我们还是先考虑最大值，很明显对于每一个点 \(k\)，我们肯定要使 \(x_k-x_s\)（\(s\) 是超级源点，\(x_s\) 是 \(0\)），尽可能大，那么 \(x_k\) 的最优取值就是从 \(s\) 开始跑最短路的 \(dis_k\)，那么答案不就是 \(\sum_{i = 1}^n dis_k\) 吗？注意是有约束的，就是每个点要保证小于等于一个数或者大于等于一个数，所以可以让超级源点向每个点连边的时候边权设置为这个数。
附个板书让大家理解一下（这里是最大值的推导，转载自我的老师shi_kan）：

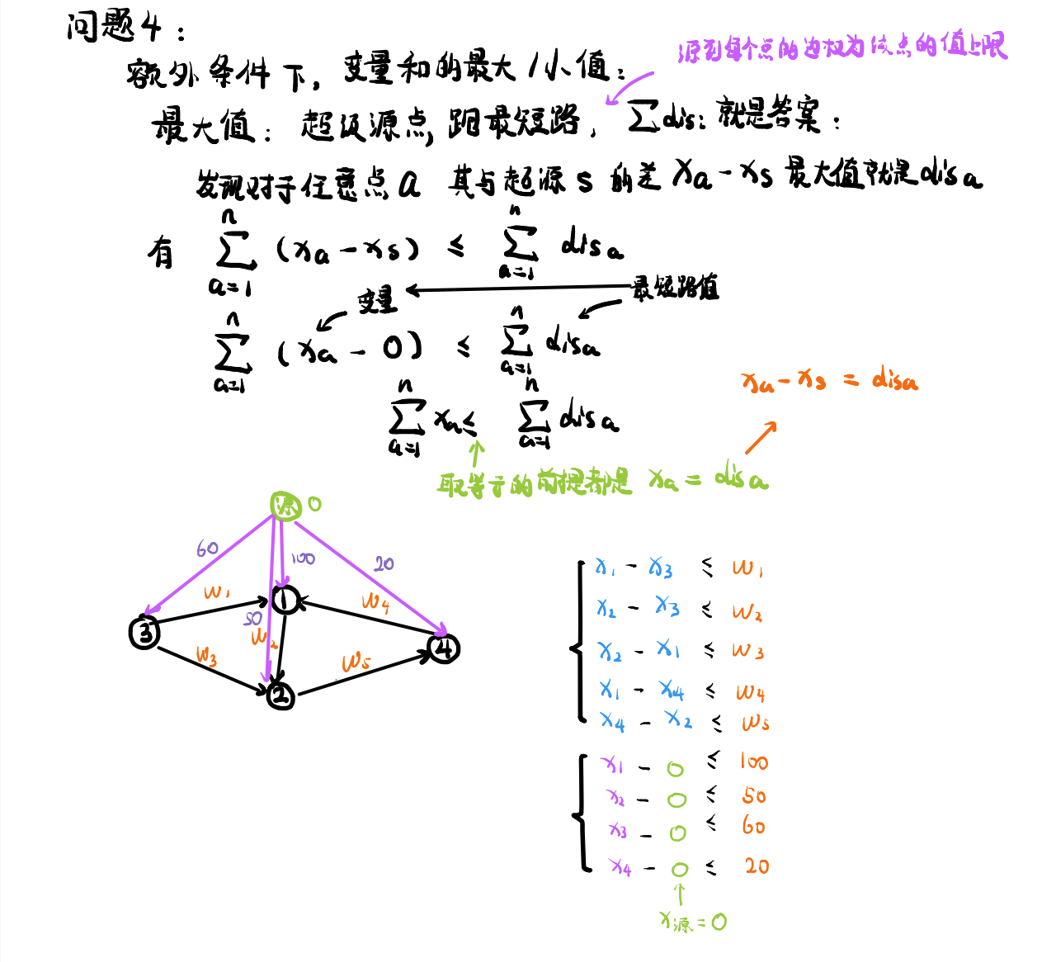
那最小值呢，完全就是跟最大值差不多的，就是建边的定义变得不同，并且改成求最长路就行了。
最小值没有板书……

六、差分约束系统板子

#include<bits/stdc++.h>
using namespace std;
const int N = ;//数据范围自己定
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
int num[N];
signed main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i = 1;i<=m;i++)
	{
		int x,y,z;
		scanf("%d %d %d",&x,&y,&z);
		a[y].push_back({x,z});
	}
	for(int i = 1;i<=n;i++)
	{
		a[0].push_back({i,0});
	}
	memset(d,0x3f,sizeof(d));
	queue<int>q;
	vis[0] = 1;
	q.push(0);
	d[0] = 0;
	while(q.size())
	{
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for(node v:a[x])
		{
			if(d[x]+v.w<d[v.x])
			{
				d[v.x] = d[x]+v.w;
				if(!vis[v.x])
				{
					vis[v.x] = 1;
					q.push(v.x);
					num[v.x]++;
					if(num[v.x] == n+1)
					{
						//无解
						return 0;
					}
				}
			}
		}
	}
	//自定义输出，d数组就是一组解
	return 0;
}

注意：这只是板子，应用时请随机应变。

七、差分约束系统例题

P5960 【模板】差分约束

差分约束系统板子题，放上代码供参考：

#include<bits/stdc++.h>
using namespace std;
const int N = 5e3+5;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
int num[N];
signed main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i = 1;i<=m;i++)
	{
		int x,y,z;
		scanf("%d %d %d",&x,&y,&z);
		a[y].push_back({x,z});
	}
	for(int i = 1;i<=n;i++)
	{
		a[0].push_back({i,0});
	}
	memset(d,0x3f,sizeof(d));
	queue<int>q;
	vis[0] = 1;
	q.push(0);
	d[0] = 0;
	while(q.size())
	{
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for(node v:a[x])
		{
			if(d[x]+v.w<d[v.x])
			{
				d[v.x] = d[x]+v.w;
				if(!vis[v.x])
				{
					vis[v.x] = 1;
					q.push(v.x);
					num[v.x]++;
					if(num[v.x] == n+1)
					{
						printf("NO");
						return 0;
					}
				}
			}
		}
	}
	for(int i = 1;i<=n;i++)
	{
		printf("%d ",d[i]);
	}
	return 0;
}

顺便说一嘴，这题数据太水了，全部数据都保证 \(n = m\)，所以说有人处理约束条件时只处理 \(n\) 个都啥事没有。

P1993 小 K 的农场

一道差分约束系统应用好题。
看第一种要求：“农场 a 比农场 b 至少多种植了 c 个单位的作物”，也就是说 \(x_a-x_b \ge c\)，转化一下 \(c \le x_a-x_b\)，然后 \(0 \le x_a-x_b-c\)，接着 \(x_b \le x_a-c\)，然后就是 \(x_b-x_a \le -c\)，不就变成了差分约束系统的方程组形式了吗（不过千万不要忘了倒着建边，否则……）？然后第二种要求本身就是差分约束系统，没什么好说的，再看第三种要求，“农场 a 与农场 b 种植的作物数一样多”，也就是 \(x_a = x_b\)，但是我们依旧可以把这个式子转化成差分约束系统，其实它相当于两个式子 \(x_a-x_b \le 0\) 和 \(x_b-x_a \le 0\)，在纸上分类讨论一下就可以知道满足这两个约束条件就一定满足 \(x_a = x_b\)，不满足这两个约束条件就一定不满足 \(x_a = x_b\)，刚好这两个约束条件符合差分约束系统的方程组形式，所以说这题的主要思路就是全部转化成差分约束系统的方程组形式。
代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 5e3+5;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
int num[N];
signed main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i = 1;i<=m;i++)
	{
		int opt,x,y,z;
		scanf("%d",&opt);
		if(opt == 1)
		{
			scanf("%d %d %d",&x,&y,&z);
			a[x].push_back({y,-z});
		}
		else if(opt == 2)
		{
			scanf("%d %d %d",&x,&y,&z);
			a[y].push_back({x,z});
		}
		else if(opt == 3)
		{
			scanf("%d %d",&x,&y);
			a[x].push_back({y,0});
			a[y].push_back({x,0});
		}
	}
	for(int i = 1;i<=n;i++)
	{
		a[0].push_back({i,0});
	}
	memset(d,0x3f,sizeof(d));
	queue<int>q;
	vis[0] = 1;
	q.push(0);
	d[0] = 0;
	while(q.size())
	{
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for(node v:a[x])
		{
			if(d[x]+v.w<d[v.x])
			{
				d[v.x] = d[x]+v.w;
				if(!vis[v.x])
				{
					vis[v.x] = 1;
					q.push(v.x);
					num[v.x]++;
					if(num[v.x] == n+1)
					{
						printf("No");
						return 0;
					}
				}
			}
		}
	}
	printf("Yes");
	return 0;
}

P2294 [HNOI2005] 狡猾的商人

跟上题差不多。
看到区间和，想到前缀和 \(sum_t-sum_{s-1} = v\)，发现这个式子可以转换成差分约束系统的方程组形式，于是这道题就做完了。
具体化简过程：

\[sum_t-sum_{s-1} = v \]

\[sum_t-sum_{s-1} \le v,sum_t-sum_{s-1} \ge v \]

\[sum_t-sum_{s-1} \le v,v \le sum_t-sum_{s-1} \]

\[sum_t-sum_{s-1} \le v,0 \le sum_t-sum_{s-1}-v \]

\[sum_t-sum_{s-1} \le v,sum_{s-1} \le sum_t-v \]

\[sum_t-sum_{s-1} \le v,sum_{s-1}-sum_t \le -v \]

于是我们就得到了两个差分约束系统的方程组形式。
多测不清空，爆零两行泪！！
清空不清下标 \(0\)，OI 必然一场空！！
尔若使 \(0\) 为超级源点，必悔矣！！
代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 105;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
int num[N];
signed main()
{
	int _;
	scanf("%d",&_);
	while(_--)
	{
		int n,m;
		scanf("%d %d",&n,&m);
		n++;
		for(int i = 0;i<=n;i++)
		{
			a[i].clear();
		}
		for(int i = 1;i<=m;i++)
		{
			int x,y,z;
			scanf("%d %d %d",&x,&y,&z);
			//sum[y]-sum[x-1] = z
			//sum[y]-sum[x-1]<=z&&sum[y]-sum[x-1]>=z
			//sum[y]-sum[x-1]<=z&&sum[x-1]-sum[y]<=-z
			a[x-1].push_back({y,z});
			a[y].push_back({x-1,-z});
		}
		for(int i = 1;i<n;i++)
		{
			a[n].push_back({i,0});
		}
		memset(d,0x3f,sizeof(d));
		memset(vis,0,sizeof(vis));
		memset(num,0,sizeof(num));
		queue<int>q;
		vis[n] = 1;
		q.push(n);
		d[n] = 0;
		int flag = 0;
		while(q.size())
		{
			int x = q.front();
			q.pop();
			vis[x] = 0;
			for(node v:a[x])
			{
				if(d[x]+v.w<d[v.x])
				{
					d[v.x] = d[x]+v.w;
					if(!vis[v.x])
					{
						vis[v.x] = 1;
						q.push(v.x);
						num[v.x]++;
						if(num[v.x] == n)
						{
							printf("false\n");
							flag = 1;
							break;
						}
					}
				}
			}
			if(flag)
			{
				break;
			}
		}
		if(!flag)
		{
			printf("true\n");
		}
	}
	return 0;
}

P3275 [SCOI2011] 糖果

这 \(5\) 个操作都可以转化，然后要求糖果的总量最小也可以套用问题 \(2\) 的做法，唯一的问题就是 \(k\) 高达 \(10^5\)，我们的做法会 TLE，由于差分约束系统是一个有向有环图，并且想到这个图边权只有 \(0\) 和 \(1\)，并且边权为 \(0\) 的边连接的点如果强连通值就不变，于是想到可以将边权为 \(0\) 的边连接的点并且强连通的点集全部缩成一个点，如果缩点后还有环，你会发现这是一个正环，然而正环跑最长路（因为是求最小值）一定是正无穷（无解），所以可以直接输出 \(-1\)，于是如果有解这个图就变成了一个有向无环图，那么就可以直接用拓扑排序求最长路了。

十年 OI 一场空，不开 long long 见祖宗！！

我的 Tarjan 学习笔记。
代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int dep[N];
int dfn[N];
int low[N];
int scc_cnt,cnt,top;
int scc_color[N];
int sta[N];
int q[N];
int f[N];
vector<node>e[N];
int num[N];
void dfs(int x)
{
	low[x] = dfn[x] = ++cnt;
	sta[++top] = x;
	for(node v:a[x])
	{
		if(!dfn[v.x])
		{
			dfs(v.x);
			low[x] = min(low[x],low[v.x]);
		}
		else if(!scc_color[v.x])
		{
			low[x] = min(low[x],low[v.x]);	
		}	
	}
	if(low[x] == dfn[x])
	{
		scc_cnt++;
		int u;
		do
		{
			u = sta[top--];
			scc_color[u] = scc_cnt;
			num[scc_cnt]++;
		}
		while(u!=x);
	}
}
signed main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i = 1;i<=m;i++)
	{
		int opt,x,y,z;
		scanf("%d %d %d",&opt,&x,&y,&z);
		if(opt == 1)
		{
			a[x].push_back({y,0});
			a[y].push_back({x,0});
		}
		else if(opt == 2)
		{
			a[x].push_back({y,1});
		}
		else if(opt == 3)
		{
			a[y].push_back({x,0});
		}
		else if(opt == 4)
		{
			a[y].push_back({x,1});
		}
		else if(opt == 5)
		{
			a[x].push_back({y,0});
		}
	}
	for(int i = 1;i<=n;i++)
	{
		a[0].push_back({i,1});
	}
	dfs(0);
	for(int i = 0;i<=n;i++)
	{
		for(node j:a[i])
		{
			if(scc_color[i] == scc_color[j.x]&&j.w)
			{
				printf("-1");
				return 0;
			}
			if(scc_color[i]!=scc_color[j.x])
			{
				e[scc_color[i]].push_back({scc_color[j.x],j.w});
				dep[scc_color[j.x]]++;
			}
		}
	}
	int h = 1,t = 0;
	for(int i = 1;i<=scc_cnt;i++)
	{
		if(!dep[i])
		{
			q[++t] = i;
		}
	}
	while(h<=t)
	{
		int x = q[h++];
		for(node v:e[x])
		{
			f[v.x] = max(f[v.x],f[x]+v.w);
			dep[v.x]--;
			if(!dep[v.x])
			{
				q[++t] = v.x;
			}
		}
	}
	long long ans = 0;
	for(int i = 1;i<=scc_cnt;i++)
	{
		ans+=(long long)f[i]*(long long)num[i];
	}
	printf("%lld",ans);
	return 0;
}

CF67A Partial Teacher

简直就是问题 \(2\) 求最小值的裸题，直接放代码了：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+5;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
char s[N]; 
signed main()
{
	int n;
	scanf("%d",&n);
	scanf("%s",s+1);
	for(int i = 1;i<n;i++)
	{
		if(s[i] == 'L')
		{
			a[i+1].push_back({i,1});
		}
		else if(s[i] == 'R')
		{
			a[i].push_back({i+1,1});
		}
		else
		{
			a[i].push_back({i+1,0});
			a[i+1].push_back({i,0});
		}
	}
	for(int i = 1;i<=n;i++)
	{
		a[0].push_back({i,1});
	}
	queue<int>q;
	vis[0] = 1;
	q.push(0);
	d[0] = 0;
	while(q.size())
	{
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for(node v:a[x])
		{
			if(d[x]+v.w>d[v.x])
			{
				d[v.x] = d[x]+v.w;
				if(!vis[v.x])
				{
					vis[v.x] = 1;
					q.push(v.x);
				}
			}
		}
	}
	for(int i = 1;i<=n;i++)
	{
		printf("%d ",d[i]);
	}
	return 0;
}

CF1131D Gourmet choice

发现普通的差分约束系统是一个数组，然而这有两个数组，但是没关系，我们把第一个数组和第二个数组合起来不就行了？然后由于问题 \(2\) 是和最小，然而这个却是最大值最小，但是你会发现和最小一定满足和最小，但是和最小不一定满足和最小，就和最小生成树和最小瓶颈树之间的关系一样。
代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 2e3+5;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
int num[N];
char s[N];
signed main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i = 1;i<=n;i++)
	{
		scanf("%s",s+1);
		for(int j = 1;j<=m;j++)
		{
			if(s[j] == '<')
			{
				a[i].push_back({j+n,1});
			}
			else if(s[j] == '>')
			{
				a[j+n].push_back({i,1});
			}
			else
			{
				a[i].push_back({j+n,0});
				a[j+n].push_back({i,0});
			}
		}
	}
	for(int i = 1;i<=n+m;i++)
	{
		a[0].push_back({i,1});
	}
	queue<int>q;
	vis[0] = 1;
	q.push(0);
	while(q.size())
	{
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for(node v:a[x])
		{
			if(d[x]+v.w>d[v.x])
			{
				d[v.x] = d[x]+v.w;
				if(!vis[v.x])
				{
					vis[v.x] = 1;
					q.push(v.x);
					num[v.x]++;
					if(num[v.x] == n+m+1)
					{
						printf("No");
						return 0;
					}
				}
			}
		}
	}
	printf("Yes\n");
	for(int i = 1;i<=n;i++)
	{
		printf("%d ",d[i]);
	}
	printf("\n");
	for(int i = n+1;i<=n+m;i++)
	{
		printf("%d ",d[i]);
	}
	return 0;
}

UVA1723 Intervals

这个题也非常的简单，跟狡猾的商人差不多，就是转化成前缀和的模式，不过这个题跟狡猾的商人不一样的是狡猾的商人要求非常严格，是等于，但是这个题只是要求大于等于，所以这个题还得加入两条限制才能对，就是对于 \(i(1 \le i \le \max_{j = 1}^n y_j)\)，\(x_i-x_{i-1} \ge 0\) 并且 \(x_{i-1}-x_{i} \ge -1\)，这样才符合题目定义和前缀和定义，然后由于这个题 \(x,y\) 可以达到 \(0\)，那么 \(x-1\) 可能达到负数，所以要让区间下标整体加 \(1\)，然后由于有了刚刚那两个约束条件，就不需要超级源点，可以直接从 \(0\) 开始跑最长路（因为是最大值最小，相当于和最小（前面说过）），原因非常简单，因为加超级源点只是为了让 SPFA 能求到所有的点，但是现在 SPFA 从 \(0\) 开始就一定能求到所有的点，所以无需添加超级源点。

但是神奇的是不加超级源点 360ms，加了超级源点 160ms，加了超级源点后快了整整 200ms，我也不知道为啥。

代码（不加超级源点）：

#include<bits/stdc++.h>
using namespace std;
const int N = 5e4+5;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
signed main()
{
	int _,maxx = 0;
	scanf("%d",&_);
	while(_--)
	{
		int n;
		scanf("%d",&n);
		for(int i = 0;i<=maxx;i++)
		{
			a[i].clear();
		}
        maxx = 0;
		for(int i = 1;i<=n;i++)
		{
			int x,y,z;
			scanf("%d %d %d",&x,&y,&z);
			y++;
			//原本x是要++的，但是既然存边的时候还是用到x-1，所以干脆不加了
			a[x].push_back({y,z});
			maxx = max(maxx,y);
		}
		for(int i = 1;i<=maxx;i++)
		{
			a[i].push_back({i-1,-1});
			a[i-1].push_back({i,0});
		}
		memset(d,-0x3f,sizeof(d));
		memset(vis,0,sizeof(vis));
		queue<int>q;
		vis[0] = 1;
		q.push(0);
		d[0] = 0;
		while(q.size())
		{
			int x = q.front();
			q.pop();
			vis[x] = 0;
			for(node v:a[x])
			{
				if(d[x]+v.w>d[v.x])
				{
					d[v.x] = d[x]+v.w;
					if(!vis[v.x])
					{
						vis[v.x] = 1;
						q.push(v.x);
					}
				}
			}
		}
		printf("%d\n",d[maxx]);
        if(_)
        {
            printf("\n");
        }
	}
	return 0;
}

提交记录。
代码（加了超级源点）：

#include<bits/stdc++.h>
using namespace std;
const int N = 5e4+5;
struct node
{
	int x;
	int w;
};
vector<node>a[N];
int d[N];
int vis[N];
signed main()
{
	int _,maxx = 0;
	scanf("%d",&_);
	while(_--)
	{
		int n;
		scanf("%d",&n);
		for(int i = 0;i<=maxx;i++)
		{
			a[i].clear();
		}
		maxx = 0;
		for(int i = 1;i<=n;i++)
		{
			int x,y,z;
			scanf("%d %d %d",&x,&y,&z);
			y++;
			//原本x是要++的，但是既然存边的时候还是用到x-1，所以干脆不加了
			a[x].push_back({y,z});
			maxx = max(maxx,y);
		}
		maxx++;
		for(int i = 1;i<maxx;i++)
		{
			a[i].push_back({i-1,-1});
			a[i-1].push_back({i,0});
		}
		for(int i = 0;i<maxx;i++)
        {
            a[maxx].push_back({i,0});
        }
		memset(d,-0x3f,sizeof(d));
		memset(vis,0,sizeof(vis));
		queue<int>q;
		vis[maxx] = 1;
		q.push(maxx);
		d[maxx] = 0;
		while(q.size())
		{
			int x = q.front();
			q.pop();
			vis[x] = 0;
			for(node v:a[x])
			{
				if(d[x]+v.w>d[v.x])
				{
					d[v.x] = d[x]+v.w;
					if(!vis[v.x])
					{
						vis[v.x] = 1;
						q.push(v.x);
					}
				}
			}
		}
		printf("%d\n",d[maxx-1]);
        if(_)
        {
            printf("\n");
        }
	}
	return 0;
}

提交记录。