Paper Reading: GRANDE: Gradient-Based Decision Tree Ensembles
Paper Reading 是从个人角度进行的一些总结分享,受到个人关注点的侧重和实力所限,可能有理解不到位的地方。具体的细节还需要以原文的内容为准,博客中的图表若未另外说明则均来自原文。
| 论文概况 | 详细 |
|---|---|
| 标题 | 《GRANDE: Gradient-Based Decision Tree Ensembles》 |
| 作者 | Sascha Marton, Stefan Ludtke, Christian Bartelt, Heiner Stuckenschmidt |
| 发表会议 | The Twelfth International Conference on Learning Representations(ICLR 2024) |
| 发表年份 | 2024 |
| 论文代码 | https://github.com/s-marton/GRANDE |
作者单位:
- University of Mannheim, Germany
- University of Rostock, Germany
研究动机
尽管深度学习在文本、图像取得了巨大成功,但在处理异构表格数据时,基于树的集成模型仍然是性能最好的方法。表格数据是现实世界中最常见的数据形式,广泛应用于医疗诊断、信用评估、欺诈检测等关键领域,因此提升表格数据模型的预测性能和鲁棒性具有显著的实际价值。现有研究表明,深度学习模型通常偏向于学习平滑的函数,而表格数据中的目标函数往往是不规则、非平滑的,这种归纳偏置的不匹配导致深度学习在大多数表格数据集上难以超越传统的树模型。
尽管像 XGBoost 这样的梯度提升树效果卓越,但它们的学习过程存在固有的限制。这类模型以顺序、贪婪的方式逐棵构建树,这限制了模型的搜索空间,可能无法找到全局最优解,并容易导致过拟合。在一定程度上,这类模型难以集成自定义的、复杂的损失函数,也不容易融入多模态学习框架中(例如,将表格数据与图像或文本结合)。一些尝试将梯度下降与树结构相互结合(如 NODE),这类方法通常为了追求可微性而牺牲了树模型的关键优势,软分割会使模型同样偏向于学习平滑解。
文章贡献
GRANDE 是一种基于梯度下降的硬性、轴对齐决策树集成模型,它通过端到端的梯度优化方法联合学习整个集成模型的所有参数。核心创新在于将决策树转化为密集可微表示,并引入了实例级权重机制,使不同决策树能够专注于处理数据的不同区域。模型采用软符号函数作为可微分分割函数,其梯度特性优于传统的 Sigmoid 和 Entmoid 函数,能为优化过程提供更合理的梯度信号。通过为每个叶节点而非整个估计器学习权重,GRANDE 实现了实例级的动态权重分配,不仅提升了模型性能还增强了局部可解释性。与需要顺序贪婪训练的传统梯度提升方法不同,GRANDE 的端到端训练方式使其能够探索更广阔的假设空间,同时避免了过度拟合问题。通过在 19 个基准数据集上的实验,结果表明其性能优于 XGBoost、CatBoost 等当前最优方法。
预备知识
本文提出的 GRANDE 建立在基于梯度的决策树 GradTree 的基础上,可以先看 GradTree 的原文,也可以看我发的另一篇博客 GradTree: Learning Axis-Aligned Decision Trees with Gradient Descent。
- Marton, Sascha, et al. "Gradtree: Learning axis-aligned decision trees with gradient descent." Proceedings of the AAAI conference on artificial intelligence. Vol. 38. No. 13. 2024.
本文方法
加权树集成
GRANDE 将 GradTree 从单个决策树扩展为树集成模型,集成模型的定义如下,其中 \(E\) 是集成中基学习器的数量,\(\omega_e\) 是对应的权重,用于对单个 GradTree 的预测加权。
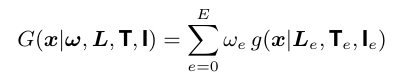
与使用软性、倾斜分割的深度学习方法(如 NODE)不同,GRANDE 保留了轴对齐分割这一对表格数据有益的归纳偏置。通过将单棵树的矩阵表示(叶子指示函数 \(L\)、分割阈值 \(T\)、特征索引 \(I\))扩展为适用于整个集成的张量表示,GRANDE 能够利用并行计算进行高效训练。与 XGBoost、CatBoost 等顺序、贪婪的 Boosting 算法不同,GRANDE 采用端到端梯度下降,联合优化集成中所有树的参数,从而克服了传统方法搜索空间受限和容易过拟合的问题。
可微分分割函数
GRANDE 面临的挑战之一是如何处理决策树的不可微操作,本文提出使用软符号函数(Softsign)作为可微分分割函数。函数的公式如下,该函数被缩放到区间 \((0, 1)\)。
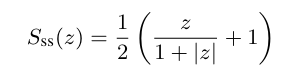
与常用的 Sigmoid 或 Entmoid 函数相比,Softsign具有更理想的梯度特性。当特征值接近分割阈值时,梯度依然显著,为优化过程提供有效信号。当特征值与阈值差距很大时,梯度不会过早地变为零,保持了模型对异常样本的响应能力。如下图所示,这种梯度行为使 Softsign 成为更优的选择,后续的消融实验也证实了其优越性。
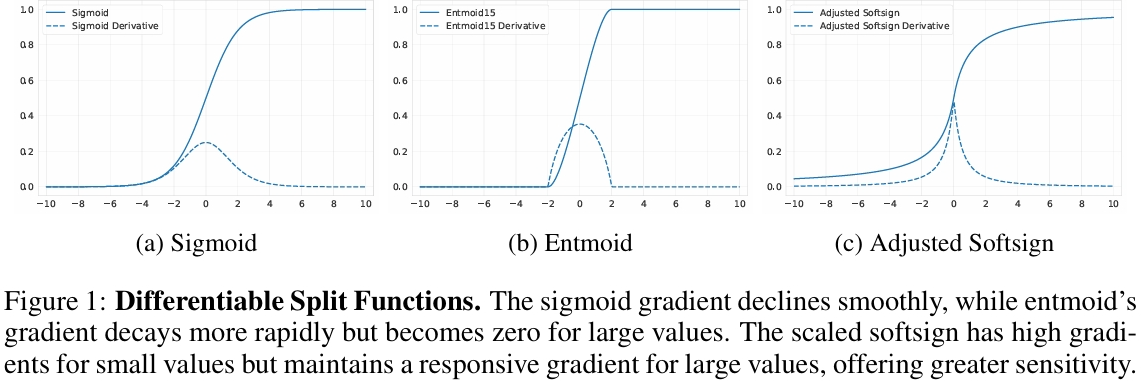
实例级估计器权重机制
经典的集成学习为每个估计器分配一个全局权重 \(\omega \in \mathbb{R}^E\) ,这使得每个树必须对所有样本做出良好预测,导致模型趋向同质化。GRANDE 引入了实例级权重机制,该机制不为整个树分配一个权重,而是为树的每个叶子节点分配一个权重,即权重张量 \(W \in \mathbb{R}^{E \times 2^{d}}\)。
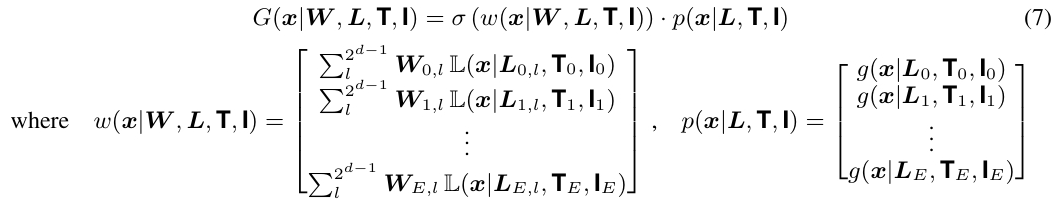
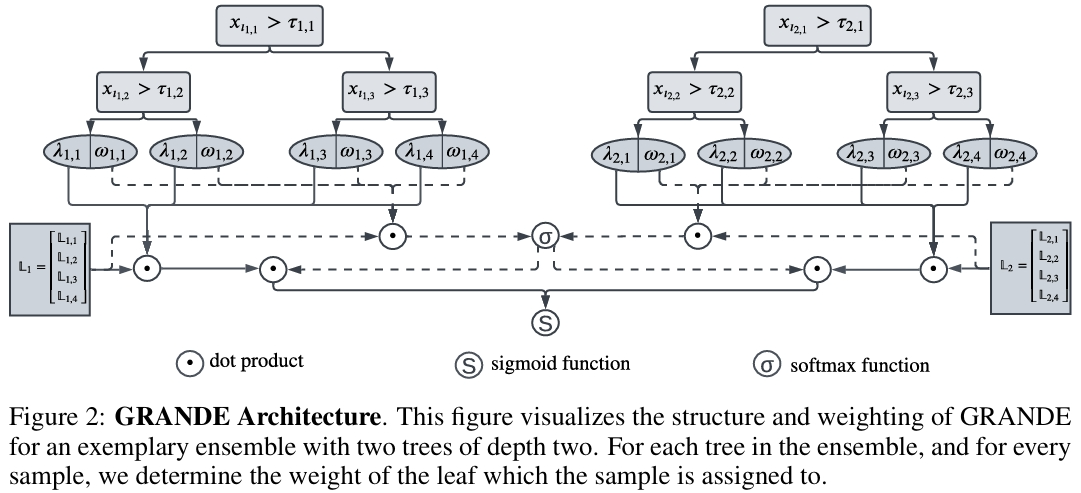
对于每个输入样本 \(x\),模型首先确定它被分配到每个树的哪个叶子节点,然后取出对应叶子的权重,形成一个针对该实例的权重向量 \(w(x) \in \mathbb{R}^E\)。最后对此权重向量应用 Softmax 函数,并与各树的预测值进行加权平均。该策略允许不同的树用于专门处理不同数据子集,从而在单一模型内学习简单规则和复杂关系的表示,既提高了性能,也增强了局部可解释性。
正则化
为了提升模型泛化能力,GRANDE 集成了多种正则化技术:
- 特征子集:每棵树仅使用随机选择的一部分特征进行训练,这也有助于改善模型在高维数据上的可扩展性。
- 数据子集:每棵树使用不同的训练样本子集(Bagging),增加集成多样性。
- Dropout:在训练过程中随机“丢弃”一部分估计器,并对剩余估计器的权重进行重新缩放,这是一种有效的正则化手段。
实验结果
数据集实验设置
数据集方面使用了 OpenML Benchmark Suites 的 19 个二元分类数据集,其基本信息如下表所示:
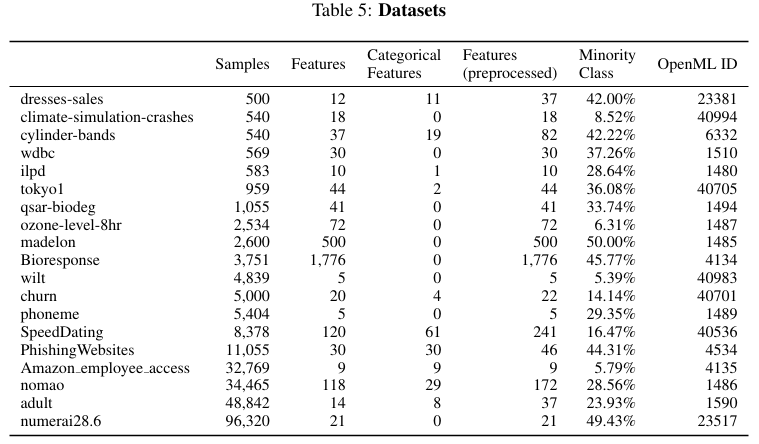
在数据预处理方面,对分类特征进行了独热编码或留一法编码,并对数值特征进行了高斯化处理(分位数转换),以适应梯度优化。对比方法选择了具有代表性的先进方法进行对比,包括集成学习算法 XGBoost、CatBoost,以及与 GRANDE 最相关的、基于梯度的分层表示方法 NODE。评估采用五折交叉验证计算测试集的 F1_macro,超参数优化使用 Optuna 进行 250 次试验,基于 5x2 交叉验证选择最佳参数。
对比实验
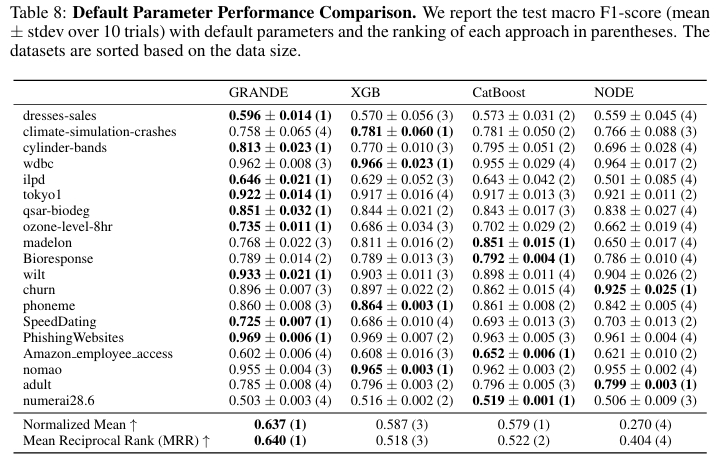
在进行了充分的超参数优化后,GRANDE 在大多数数据集上表现最佳,获得了最高的平均倒数排名(MRR = 0.702)和最高的归一化平均性能(0.776)。
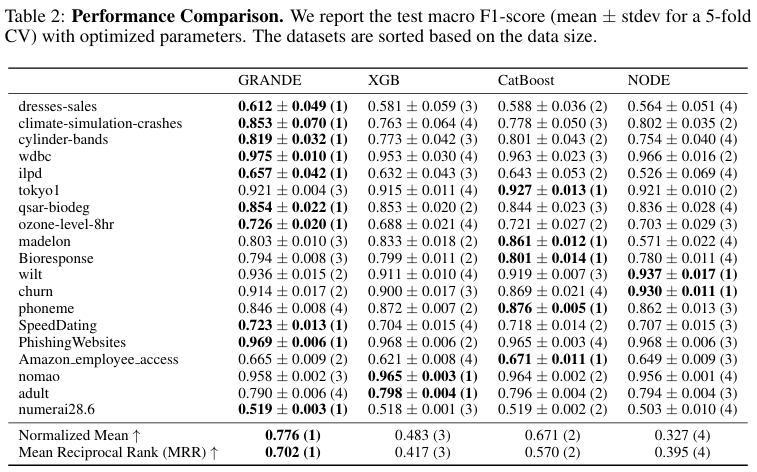
许多深度学习方法严重依赖超参数调优,GRANDE 在默认参数设置下依然取得了最高的归一化平均性能(0.637)和 MRR(0.640)。
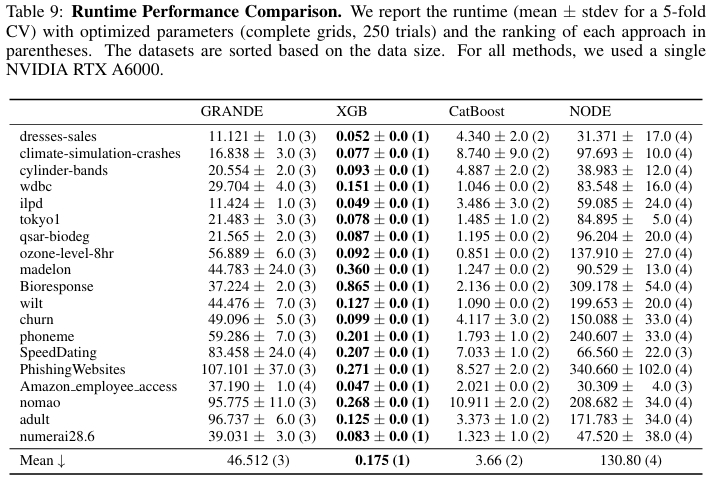
计算效率
GRANDE 在保证性能的同时也兼顾了效率,它在所有数据集上的平均训练时间为 47 秒,最大为 107 秒。GRANDE 的运行时间显著低于同为梯度方法的 NODE,但比高度优化的 GBDT 框架要慢。
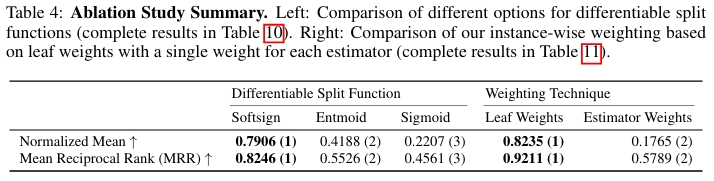
消融实验
对于 Softsign 分割函数,与 Sigmoid 和 Entmoid 函数相比,使用 Softsign 作为可微分分割函数带来了显著的性能提升,说明其梯度特性更适合决策树的学习。在实例级权重方面,将每个估计器一个权重的方案与 GRANDE 的基于叶子的实例级权重方案进行对比。结果表明实例级权重机制通过促进集成多样性,允许不同的树专注于数据的不同区域,从而显著提高了模型性能。
可解释性分析
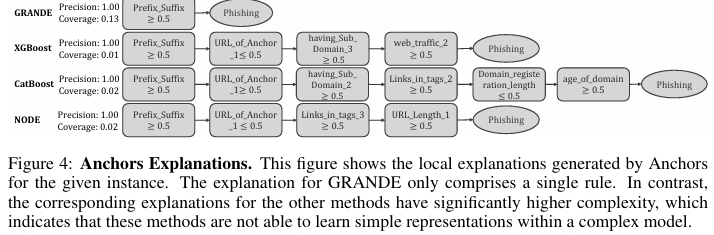
以 PhishingWebsites 数据集为例,数据集中存在一些明确的钓鱼网站指示规则(如在域名中添加前缀或后缀)。GRANDE 成功学习到了这些简单规则,并将高权重(94%)分配给了一个仅包含该规则的浅层决策树。对于符合该规则的样本,预测主要由一个简单的、易于理解的树做出,这使得用户可以理解模型的决策依据。

使用模型无关的解释工具 Anchors 进行分析,发现 GRANDE 的预测规则非常简单(仅一条规则),且精度高(1.00)、覆盖范围广。而其他方法的解释则复杂得多,表明 GRANDE 能够在复杂模型中有效地学习和利用简单规则。
优点和创新点
个人认为,本文有如下一些优点和创新点可供参考学习:
- GRANDE 通过密集张量表示和直通估计器,实现了对硬性、轴对齐决策树集成的端到端梯度下降训练,将树模型的有益归纳偏置与梯度优化的灵活性结合;
- 采用软符号函数作为可微分分割函数,其独特的梯度特性(对接近阈值的值敏感,对远离阈值的值保持响应)为决策树学习提供了更合理的梯度信号;
- 通过为每个叶节点而非整个估计器学习权重,实现了动态的实例级权重分配,使模型能够学习"局部专家"树,显著提升了集成多样性和局部可解释性。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号