Paper Reading: GradTree: Learning Axis-Aligned Decision Trees with Gradient Descent

目录

• 研究动机
• 文章贡献
• 预备知识
  • Entmax 函数
  • Hardmax 函数
• 本文方法
  • 公式描述
  • 稠密决策树表示
  • 决策树损失的反向传播
    • 针对 C1
    • 针对 C2
    • 针对 C3
• 实验结果
  • 数据集和实验设置
  • 分类性能
  • 模型复杂度、参数鲁棒性、计算效率
  • 消融实验
• 优点和创新点

Paper Reading 是从个人角度进行的一些总结分享，受到个人关注点的侧重和实力所限，可能有理解不到位的地方。具体的细节还需要以原文的内容为准，博客中的图表若未另外说明则均来自原文。

论文概况	详细
标题	《GradTree: Learning Axis-Aligned Decision Trees with Gradient Descent》
作者	Sascha Marton, Stefan Ludtke, Christian Bartelt, Heiner Stuckenschmidt
发表会议	The Thirty-Eighth AAAI Conference on Artificial Intelligence (AAAI-24)
发表年份	2024
会议等级	CCF-A
论文代码	https://github.com/s-marton/GradTree

作者单位：

1. University of Mannheim, Germany
2. University of Rostock, Germany

研究动机

决策树模型因其高度可解释性而备受青睐，但其主流的学习算法却存在固有的优化缺陷​​。CART、C4.5 等贪心算法一直是学习决策树的标准方法，这些算法通过​​局部优化​​策略，在树的每个内部节点上独立地选择最优分裂。然而，这种“步步为营”的策略存在弱点：

1. ​​陷入局部最优​​：每一步的局部最优选择并不一定能导向全局最优的树结构，贪心算法过早地做出不可逆的决策，极大地约束了搜索空间。
2. 模型性能受限​​：由于搜索不充分，贪心算法学到的树可能无法捕捉数据中复杂的特征交互关系，从而限制了其预测性能的上限。

现有的非贪心方法也存在各种问题，无法很好地解决缺陷：

非贪心决策树方法	不足
最优决策树方法	旨在寻找全局最优解，但通常计算复杂度极高并且容易过拟合
进化算法	虽然能进行全局搜索，但通常计算成本昂贵，且结果可能不稳定
倾斜决策树​​	实现了可微的决策树，但却​​牺牲了模型的可解释性​​

文章贡献

本文提出了一种名为 GradTree 的决策树算法，实现了对硬、轴对齐决策树所有参数的联合优化。通过一种新颖的稠密决策树表示法，将离散的树参数（如分裂特征索引和阈值）转化为连续、可微的矩阵形式。为了克服决策树固有的不可微性挑战，GradTree 运用了直通算子和 entmax 变换，使得在前向传播中保持硬决策的同时，在反向传播中能够计算梯度并进行有效的参数更新。这种方法本质上将深度学习的梯度下降优化引入到了决策树的学习中，使得模型能够跳出传统贪心算法局部最优的局限，寻找泛化性能更好的解。在多个数据集上对 GradTree 进行了经验评估，GradTree 在二分类任务上优于对比方法，并在多类数据集上取得了有竞争力的结果。

预备知识

Entmax 函数

​​Softmax​​ 是神经网络中最常用的激活函数，它将一个实数向量（logits）转换成一个概率分布，最常用于多分类问题的输出层。该函数的特性是​​处处稠密​​，只要 logits 值不是无穷大，Softmax 对每一个元素都会分配一个非零的概率，无论这个概率多小。在某些任务中，这种的特性并不是优点。例如在机器翻译或摘要生成中，我们更希望模型能够​​聚焦​​于少数几个相关的单词，而完全忽略其他不相关的单词。Softmax 产生的微弱概率可以看作是“噪声”。
为了解决这个问题，Sparsemax 函数被提出，它的目标是产生一个稀疏的概率分布​​，即将一部分元素的概率直接置为 0。Sparsemax 对 logits 向量进行一个​​欧几里得投影​​，这个投影过程会找到一个分布使得它与 logits 的欧氏距离最小。输出一个概率分布中，其中一部分概率严格大于 0，另一部分严格等于 0，这实现了“聚焦”机制。
Entmax 的核心贡献是将 Softmax 和 Sparsemax 统一到了一个函数家族中，并通过一个参数 α（alpha）来控制稀疏程度。Entmax 函数的通用形式由以下优化问题定义：

\[\text{entmax}_\alpha(\mathbf{z}) = \arg\max_{\mathbf{p} \in \Delta^{d-1}} \mathbf{p}^\top \mathbf{z} + H_\alpha^\mathrm{Tsallis}(\mathbf{p}) \]

其中相关的符号含义如下：

符号	含义
\(\mathbf{z}\)	输入 logits 向量
\(\Delta^{d-1}\)	概率单纯形
\(H_\alpha^\mathrm{Tsallis}\)	Tsallis α-熵

对于 α 参数，它的几种取值的含义为：

1. 当 ​​α = 1​​ 时，Tsallis 熵退化为香农熵​​，此时的 Entmax 就是标准的 ​​Softmax​​ 函数。
2. 当 ​​α = 2​​ 时，Entmax 变成 ​​Sparsemax​​ 函数，输出是稀疏的。
3. 当 ​​α > 1​​ 时，随着 α 的增大，输出的稀疏性会​​增强​​（更多的值变为 0）。
4. 当 ​​α < 1​​ 时，理论上会产生“稀疏性”，但概率可能为负，不符合分布要求，所以通常只关注 α ≥ 1 的情况。

Entmax 函数具有以下一些有点：

1. 能够使模型不需要依赖外部设计的启发式方法，使其​​根据数据自适应学习稀疏模式；
2. 在​​注意力机制​​中应用 Entmax（替换 Softmax）后，得到的注意力权重图会非常稀疏，实现提高可解释性；
3. 在一些任务中，特别是需要模型做出“硬决策”的任务上（如文本生成、关系抽取），强制模型聚焦于关键信息可以带来性能的提升；
4. 权重为 0 的部分在后续计算中可以跳过，能够提升计算效率。

Hardmax 函数

Hardmax​​ 是一个将输入向量转换为​​ one-hot 编码​​的函数，它会找到输入向量中最大元素的位置并将其设为 1，其他所有位置都设为 0。其公式定义为：

\[\text{hardmax}(z)_i = \begin{cases} 1 & \text{if } i = \arg\max_j z_j \\ 0 & \text{otherwise} \end{cases} \]

Hardmax 是​​决策函数​​，不是​​激活函数​​，主要用于​​推理阶段​​获得确定性决策。在训练中需要通过 STE、Gumbel-Softmax 等技巧才能使用，相比于 Entmax，Hardmax 的稀疏性是最极端的（只有一个非零值）。

本文方法

公式描述

通过基于算术运算的决策树表示方法可以将传统规则嵌套结构转换为可微分的加法和乘法运算形式。本文方法的定义涉及以下核心参数，其中 \(d\) 为树深度，\(2^d-1\) 为内部节点数，\(2^d\) 为叶节点数。

参数	符号	说明
分裂阈值向量	\(\tau \in \mathbb{R}^{2^d-1}\)	包含所有内部节点的分裂阈值
特征索引向量	\(\iota \in \mathbb{N}^{2^d-1}\)	表示每个内部节点选择的分裂特征索引
叶节点预测向量	\(\lambda \in \mathcal{C}^{2^d}\)	存储每个叶节点的类别预测

决策树被定义为函数 \(DT(x \mid \tau, \iota, \lambda): \mathbb{R}^n \rightarrow \mathcal{C}\)，如下公式所示。

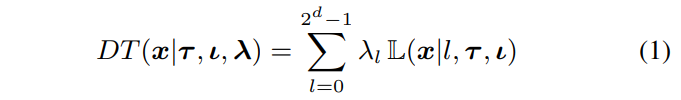
分裂函数 S 采用 Heaviside 阶跃函数形式，如下公式所示。其中 \(\iota\) 是在某个分割处考虑的特征的索引，\(\tau\) 是对应的阈值。

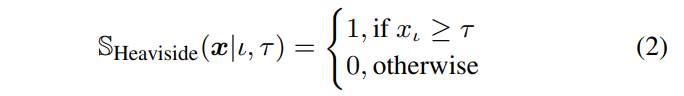
函数 $ L $ 表示样本 $ x \in \mathbb{R}^{n}$ 是否属于叶子 $ l $，可以定义为前一个内部节点的分裂函数的乘积。

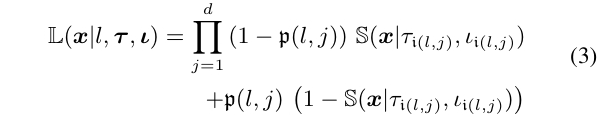
对于深度为 $ j $ 的叶节点 $ l $，其路径上的内部节点索引通过广度优先排序确定：

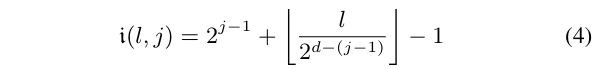
参数 \(\mathfrak{p}(j,l)∈\{0,1\}\) 表示在深度 $ j $ 走向左分支（0）还是右分支（1）：

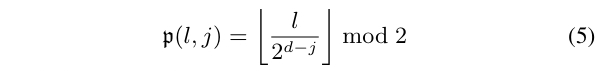
该部分指出了三个阻碍梯度优化的问题：

1. C1 特征索引离散性：\(\iota \in \mathbb{N}\) 无法直接梯度更新；
2. C2 分裂函数不可微：Heaviside 函数梯度为零或未定义；
3. C3 叶节点预测离散性：\(\lambda \in \mathcal{C}\) 无法计算损失梯度。

稠密决策树表示

在传统的决策树表示中，每个内部节点通常只存储一个​​特征索引​​和一个​​分割阈值​​。这种稀疏表示存在两大优化障碍：特征索引是离散的、不可微的，无法通过梯度下降直接优化；单个阈值参数需要服务于所有特征，但不同特征具有不同的值域和分布，一个适用于某个特征的阈值可能对另一个特征毫无意义。为了解决传统决策树稀疏表示无法进行梯度优化的问题，GradTree 引入了稠密矩阵来表示决策树的参数。

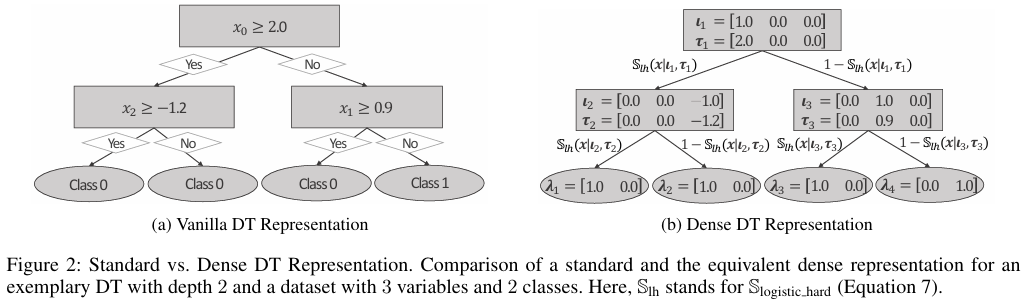
具体包括两个关键组件：特征选择矩阵、阈值矩阵：

1. 特征选择矩阵\(I\)：传统方法的特征选择被表示为一个向量，GradTree 将其扩展为一个维度为 \(I \in \mathbb{R}^{2^d-1} \times \mathbb{R}^n\) 的矩阵，其中 \(2^d-1\) 为内部节点数，\(n\) 为特征总数。对每个节点的特征索引进行​​独热编码​​，例如若某个节点选择第 $ k $ 个特征，则该节点对应的行向量是一个长度为 $ n $ 的向量，其中第 $ k $ 个元素为 1，其余元素为 0。该组件将离散的特征选择问题转化为对连续向量的优化问题，从而变得可微，解决了问题 C1。
2. 阈值矩阵\(T\) ：传统方法的阈值被表示为一个向量，GradTree 将其扩展为一个维度为 \(T \in \mathbb{R}^{2^d-1} \times \mathbb{R}^n\) 的矩阵。每个节点对应一个长度为 $ n $ 的向量，为​​每一个特征都存储一个潜在的分割阈值​​。该操作使得每个特征都有自己的阈值参数，避免了不同特征间阈值冲突的问题。优化器可以为每个特征独立地学习合适的阈值,即使某个特征在当前节点未被选中，其阈值参数也会被保留。这相当于一个记忆机制，确保在后续优化中，如果特征选择发生变化，之前学到的阈值信息不会丢失，增强了优化的稳定性。

在稠密表示下，分裂函数被重新定义为如下公式，其中 \(\sigma\) 是逻辑斯蒂函数，\(\left\lfloor ⋅ \right\rceil\) 表示四舍五入到最接近的整数。

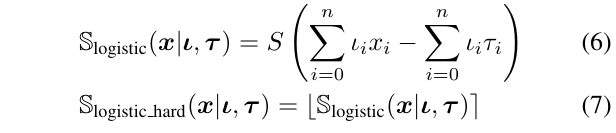
决策树损失的反向传播

该章节旨在解决问题 C1-C3，使传统的硬性、轴对齐决策树能够利用反向传播进行学习。

针对 C1

针对 C1：特征索引的离散性（\(\iota \in \mathbb{N}\)），GradTree 结合​​直通算子​​与 ​​entmax 变换​​进行解决：

• 前向传播​​：对每个节点的特征选择权重（即稠密表示矩阵 \(I\) 中的行向量）应用 entmax 变换以获得稀疏分布，然后使用 hardmax 将其变为独热编码，确保硬性的特征选择。
• 反向传播：使用直通算子，绕过 hardmax 操作，梯度直接传递给 entmax 的输出，从而更新特征选择权重。

entmax 能产生稀疏的概率分布，使得某个特征的权重远高于其他特征，减少了前向传播（硬选择）与反向传播（软权重）之间的不匹配，让梯度优化更有效。

针对 C2

针对 C2 分裂函数的不可微性（Heaviside 阶跃函数），GradTree 结合​​使用​​可微近似​​与​​直通算子​​：

• ​​前向传播​​：使用重构的分裂函数 \(S_{\text{logistic\_hard}}\)，即先通过 Sigmoid 函数计算连续值，再四舍五入得到硬决策（0 或 1）；
• ​​反向传播​​：再次使用直通算子，忽略四舍五入操作，梯度基于 Sigmoid 函数的导数进行传播。

Sigmoid 函数平滑可微，其梯度包含了样本特征值与分裂阈值之间“距离”的信息。距离阈值越近的样本，产生的梯度越大，模型参数调整的幅度也越大，这使得学习过程更加精细和高效。

针对 C3

针对 C3：叶节点预测的离散性（\(\lambda \in \mathcal{C}\) ），GradTree 的叶节点参数不再是一个类别标签 \(\lambda \in \mathcal{C}\)，而是一个类别概率分布 \(\lambda \in \mathbb{R}^c\)。这使得可以使用标准的可微损失函数（如交叉熵损失）来计算损失并产生梯度，从而通过反向传播来优化每个叶节点的“类概率”参数。
上述策略被整合到​​算法 1 中，如伪代码所示。

实验结果

数据集和实验设置

本文使用了多个 UCI 数据集，涵盖二元分类和多元分类任务。数据进行了标准预处理，包括留一法编码分类特征、分位数变换使特征符合正态分布，以及使用 SMOTE 技术处理类别不平衡的数据集。评估采用 80%/20% 的训练-测试分割，并使用​​ F1_macro 分数​​作为主要评估指标，重复 10 次计算均值±标准差。

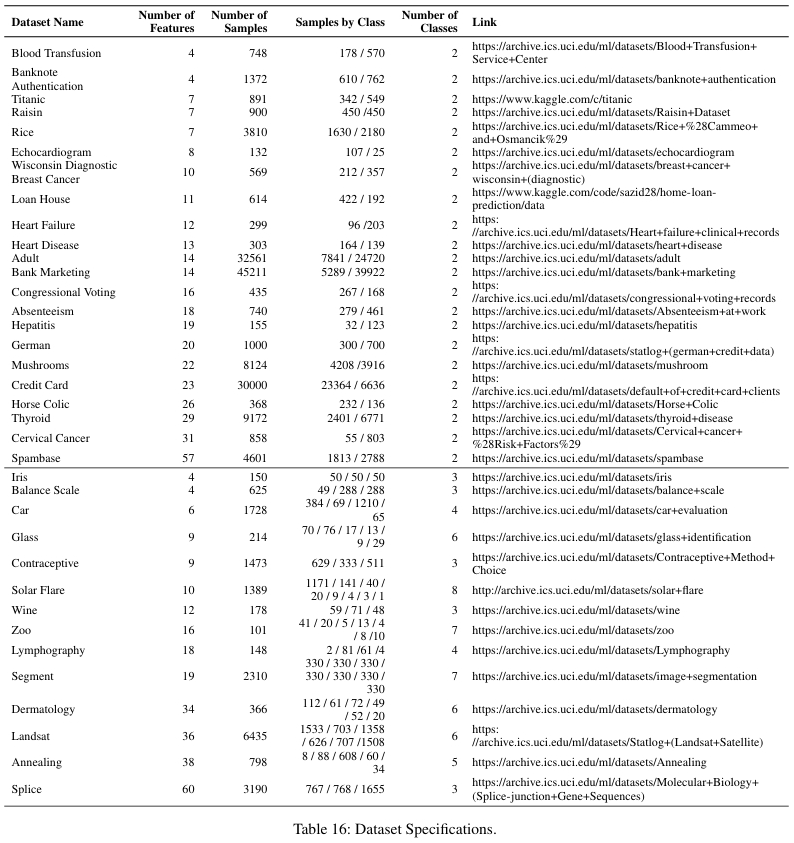
本文的对比算法包括以下 4 个：

对比算法	描述
​​CART​​	贪心算法的代表，使用 scikit-learn 实现
GeneticTree​​	进化算法（非贪心）的代表
DNDT​​	基于梯度的软决策树方法，是 GradTree 最直接的对比基准
​​DL8.5​​	最优决策树方法的代表（使用动态规划）

分类性能

论文使用​​平均相对差异 MRD 和​​平均倒数排名 MRR 来综合评估性能，实验结果如下表所示。可见 GradTree 在二分类问题上取得了最佳的整体性能，在多分类数据集上位列第二。GradTree 在特征数较少的数据集上能领先，但在高维、多类数据集上 CART 表现更好，可能是因为 GradTree 的稠密表示参数随特征和类别数增长，增加了优化难度。


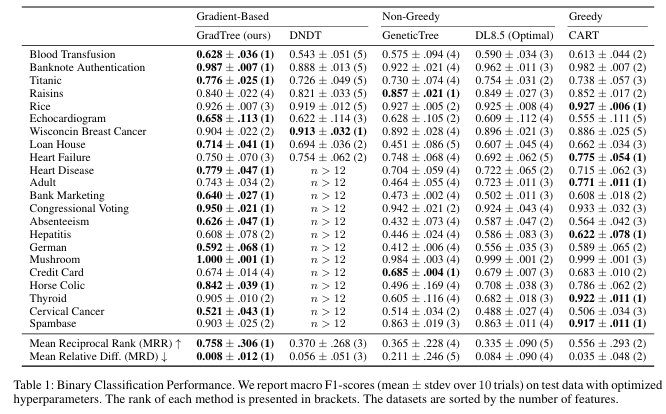
在过拟合控制方面，通过比较训练 F1 分数和测试 F1 分数的差距来衡量过拟合程度。GradTree 的过拟合程度显著低于其他非梯度方法，说明梯度下降优化有助于找到泛化性能更好的局部最优解，而贪心方法更容易在训练集上过拟合。

模型复杂度、参数鲁棒性、计算效率

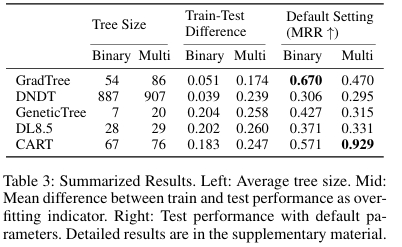
在树的规模方面，可见 GradTree 能产生紧凑的模型。经过后剪枝，GradTree 在二分类任务上的​​有效树尺寸​​小于 CART，在多分类任务上略大于 CART。
在超参数设施方面，即使在未经大量调优的默认参数设置下，GradTree 在二分类任务中仍能取得最高的 MRR 和最多次的最佳性能，表明其并不依赖繁琐的超参数搜索。
在计算效率方面，​​CART ​​训练速度最快（<1 秒），GradTree ​​平均训练时间约为 35 秒，对于大多数数据集是可接受的（<30 秒），与 DNDT 相当。

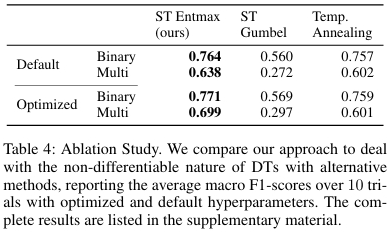
消融实验

论文进行了消融实验，验证了其核心设计——​​“ST entmax”​​ 的有效性。该方法被与两种替代方案对比：ST Gumbel Softmax​​、温度退火 entmax​。实验结果表明，本文采用的​​ ST entmax 方法在优化后的性能和默认参数下的稳定性上均优于其他方案​​。

优点和创新点

个人认为，本文有如下一些优点和创新点可供参考学习：
​​1. 提出了稠密决策树表示法，将离散的树参数转化为连续可微的矩阵形式；
​​2. 使用直通算子结合 entmax 变换，解决了特征选择和硬分裂决策的不可微问题，实现端到端梯度传播​；
​​3. 在保持轴对齐硬分裂的高可解释性前提下，实现了决策树参数的全局联合优化，突破了传统贪心算法的局部最优限制。​