Fourier,lapalace,z的理解（一）

转自：链接：https://www.zhihu.com/question/22085329/answer/774074211
作者：DBinary

傅里叶级数推导

法国数学家傅里叶在提出傅里叶级数时认为，任何一个周期信号都可以展开成傅里叶级数，之后这个结论被进一步补充，只有在满足狄利克雷条件时，周期信号才能够被展开成傅里叶级数。

其中，狄利克雷条件的定义如下：

在一周期内，连续或只有有限个第一类间断点。
在一周期内，极大值和极小值的数目应是有限个。
在一周期内，信号是绝对可积的。

现假设一函数 $f\left( t \right)$ 由一个直流分量和若干余弦函数组成，如式2.10所示

$f\left( t \right) = c_{0} + \sum_{n = 1}^{\infty}{c_{n}\cos}\left( n\omega t + \varphi \right)\text{ } (2.10)$

利用三角函数的和差化积公式,上式可以进一步变形为

$f\left( t \right) = c_{0} + \sum_{n = 1}^{\infty}{\left\lbrack c_{n}\text{cosφ}\cos\left( \text{nωt} \right) - c_{n}\text{sinφ}\sin\left( \text{nωt} \right) \right\rbrack\ \ \ (2.11)}$

设 $a_{n},\ b_{n}$ 为:

$a_{n} = c_{n}cos\varphi\ \ \ (2.12)$

$b_{n} = - c_{n}sin\varphi\ (2.13)$

那么,式2.11可写作

$f\left( t \right) = c_{0} + \sum_{n = 1}^{\infty}{\left\lbrack a_{n}\cos\left( \text{nωt} \right) + b_{n}\sin\left( \text{nωt} \right) \right\rbrack\ \ \ (2.14)}$

式2.14实际上即是傅里叶级数的展开式,从上式可知,若要将一个周期信号展开为傅里叶级数形式,实现上就是确定级数 $a_{n}b_{n}$ ，那么就下来我们讨论的就是如何求出 $a_{n}b_{n}$ 。

在式2.14的两边同时乘以一个 $\sin\left( \text{kωt} \right),$ 并对它们在一个周期内进行积分,那么就有

$\int_{0}^{T}{f\left( t \right)}\sin\left( \text{kωt} \right)dt = \int_{0}^{T}{c_{0} \sin\left( \text{kωt} \right)\text{dt}} + \int_{0}^{T}{\sin\left( \text{kωt} \right) \sum_{n = 1}^{\infty}{\left\lbrack a_{n}\cos\left( \text{nωt} \right) + b_{n}\sin\left( \text{nωt} \right) \right\rbrack\text{dt}}\ (2.15)}$

根据第一节的推论，频率不同的三角函数相乘在一个周期内的积分必定为0,因此,仅有k=n时不为0,那么其中 $\int_{0}^{T}{c_{0} \sin\left( \text{kωt} \right)\text{dt}}$ 结果为0, $\int_{0}^{T}{a_{n} \cos\left( \text{nωt} \right)sin\left( \text{kωt} \right)\text{dt}}$ 结果也必定为0,因此上式可以进一步化简为

$\int_{0}^{T}{f\left( t \right)}\sin\left( \text{kωt} \right)dt = b_{n}\int_{0}^{T}{\sin\left( \text{nωt} \right)}^{2}dt = b_{n}\frac{T}{2}\ \ \ \ (2.16)$

因此,得出

$b_{n} = \frac{2}{T}\int_{0}^{T}{f\left( t \right)\sin\left( \text{nωt} \right)}\text{dt}\ \ \ \ (2.17)$

依照上诉方法,同样可以计算出

$a_{n} = \frac{2}{T}\int_{0}^{T}{f\left( t \right)\cos\left( \text{nωt} \right)\text{dt}}\ \ (2.18)$

同时,通过以下公式可以得知傅里叶级数与波幅相位之间的关系

$c_{n} = \sqrt{{a_{n}}^{2} + {b_{n}}^{2}}\ \ \ \ (2.19)$

$\varphi = \arctan\left( - \frac{b_{n}}{a_{n}} \right) (2.20)$

复变函数到傅里叶级数

常用复数函数表达式：

$e^{\text{jθ}} = cos\theta + jsin\theta$

其中公式中e是自然对数的底，i是虚数单位。

该函数将复数、指数函数与三角函数相互联系起来。如果定义一个复平面，其中以横坐标方向作为实数方向，纵坐标方向作为虚数方向，复变函数实际上是一个绕原点旋转的一个圆，如图2.3.1：

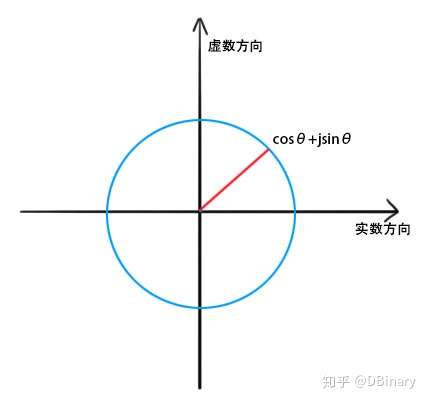图2-3-1 复平面坐标系

由公式

$\theta = \omega t = \frac{2\pi}{T}\text{ }(2.21)$

可知，该复变函数可以看做是一个角速度为 $w$ 周期为T在复平面上绕原点旋转的半径为1的圆。将公式代回到复变函数中，那么，复变函数可以写成公式2.22的形式

$e^{\text{jω}t} = cos\omega t + jsin\omega t\text{ }(2.22)$

设一组三角函数，其频率是 $\text{cosω}t$ 的n倍，其中n是大于0的正整数，那么可以定义这一组三角函数为：

$\cos\left( \text{nwt} \right) = \frac{e^{\text{jnωt}} + e^{- jn\omega t}}{2}\text{ }(2.23)$

$\sin\left( \text{nwt} \right) = \frac{e^{\text{jnωt}} - e^{- jn\omega t}}{2j}\text{ }(2.24)$

将公式2.23与2.24代回到式2.14中，可得到如下公式

$f\left( t \right) = c_{0} + \sum_{n = 1}^{\infty}\left\lbrack a_{n}\frac{e^{\text{jnωt}} + e^{- jn\omega t}}{2} + b_{n}\frac{e^{\text{jnωt}} - e^{- jn\omega t}}{2j} \right\rbrack(2.25)$

进一步化简可以得到:

$f\left( t \right) = c_{0} + \sum_{n = 1}^{\infty}{\lbrack\frac{\left( a_{n} - jb_{n} \right)}{2}e^{\text{jn}\omega t} + \frac{\left( a_{n} + jb_{n} \right)}{2}e^{- jn\omega t}\rbrack}\ (3.26)$

因为

$a_{- n} = \frac{2}{T}\int_{0}^{T}{f\left( t \right)\cos\left( - n\omega t \right)\text{dt}} = a_{n}\ \ (3.27)$

$b_{- n} = \frac{2}{T}\int_{0}^{T}{f\left( t \right)\sin\left( - n\omega t \right)}dt = - b_{n}\ \ \ \ (3.28)$

因此，上式可变为

$f\left( t \right) = c_{0} + \sum_{n = 1}^{\infty}{\lbrack\frac{\left( a_{n} - jb_{n} \right)}{2}e^{\text{jn}\omega t} + \frac{\left( a_{- n} - jb_{- n} \right)}{2}e^{- jn\omega t}\rbrack}\ (3.29)$

即

$f\left( t \right) = c_{0} + \sum_{n = 1}^{\infty}{\frac{\left( a_{n} - jb_{n} \right)}{2}e^{\text{jn}\omega t}} + \sum_{- \infty}^{- 1}{\frac{\left( a_{n} - jb_{n} \right)}{2}e^{\text{jn}\omega t}}$

$f\left( t \right) = \sum_{n = - \infty}^{\infty}{\frac{\left( a_{n} - jb_{n} \right)}{2}e^{\text{jnωt}}}\ (3.30)$

设 $A_{n} = \frac{\left( a_{n} - jb_{n} \right)}{2}$ 上式就写成了

$f\left( t \right) = \sum_{n = - \infty}^{\infty}{A_{n}e^{\text{jnωt}}}\ \ \ (3.31)$

式3.31就是复数形式的傅里叶级数,其中, $\ A_{n}$ 是一个复数,在式3.31的两边同时乘以一个 $e^{- jk\text{ωt}}$ ,并对它们在一个周期内进行积分,得到式子3.32

$\int_{0}^{T}{f(t)e^{- jk\omega t}}dt = \int_{0}^{T}{\sum_{n = - \infty}^{+ \infty}{A_{n}e^{j(n - k)\omega t}}}dt\ (3.32)$

由第一节的正交性推论可知,当n与k不相等时,积分结果必定为0,仅当 $n = k$ 时,右表达式有值,因此,推导出3.33

$\int_{0}^{T}{f(t)e^{- jn\omega t}}dt = A_{n}T$

即得出复数 $A_{n}$ 的求法

$A_{n} = \frac{1}{T}\int_{0}^{T}{f(t)e^{- jn\omega t}}dt\ \ \ (3.33)$

通过求 $A_{n}$ 的模(式2.19),可求得该频率波的幅值的一半

${|A}{n}| = \frac{1}{2}\sqrt{{a{n}}^{2} + {b_{n}}^{2}} = \frac{1}{2}c_{n}\ \ (3.34)$

而通过对其虚部与实部反正切,就可以求得该频率波的相位。

周期离散时间傅里叶变换

傅里叶级数适用于周期时间连续且无限长度的信号处理。但是我们需要对待处理信号进行采样，并且信号常常并非是周期的，同时采样时间也不可能是无穷长，这就意味着我们需要一个能够处理非周期离散时间信号的变换公式。

现假设我们对周期连续信号等间距采样，同时保证采样的结果也是周期性的，设离散时间的采样样本为 $x\lbrack t\rbrack$ ,其周期为T,那么,其应该频率是 $\frac{2\pi}{T}$ ,同时因为其周期性,其应该满足式3.35

$x\left\lbrack t \right\rbrack = x\left\lbrack t + kT \right\rbrack\text{}(3.35)$

其中,n、k是一个整数,设 $t=<T>$ 表示任意连续的T个采样点，即一个周期内的所有样本点，那么根据式3.31，周期离散傅里叶级数可以写成3.36这种形式

$x\left\lbrack t \right\rbrack = \sum_{t = < T >}^{}{A_{n}e^{\text{jnωt}}}\text{}(3.36)$

其中$$A_{n}$$就是周期离散傅里叶级数的系数，根据第三节的推导方式，在式子的两边同时乘以 $e^{- jk\text{ωt}}$ 得到式子3.37

$x\left\lbrack t \right\rbrack e^{- jk\text{ωt}} = \sum_{t = < T >}^{}{A_{n}e^{\text{jnωt}}e^{- jk\text{ωt}}}\text{ }(3.37)$

然后再同时对两边进行N项上求和，得到3.38

$\sum_{t = < T >}^{}{x\left\lbrack t \right\rbrack e^{- jk\text{ωt}}} = \sum_{t = < T >}^{}{A_{n}\sum_{t = < T >}^{}e^{j(n - k)\omega t}}$

上式同样满足当n不等于k时,周期的累加和为0,因此,上式可变为

$\sum_{n = < T >}^{}{x\left\lbrack t \right\rbrack e^{- jk\text{ωt}}} = TA_{n}\ (3.38)$

因此,可得到

$A_{n} = \frac{1}{T}\sum_{t = < T >}^{}{x\left\lbrack t \right\rbrack e^{- jn\text{ωt}}}\text{ }(3.39)$

非周期离散时间傅里叶变换

假设一个离散时间信号,其只在区间[1,3]上有值,其它范围都是0,那么,我们就可以把它当做一个周期无穷大的信号,那么,我们就可以套用公式3.39,取得其傅里叶级数公式3.40

$A_{n} = \frac{1}{3}\sum_{t = 1}^{3}{x\left\lbrack t \right\rbrack e^{- jn\text{ωt}}}\text{}(3.40)$

因为在其它区间内的都是0,因此上式又可以写成

$A_{n} = \frac{1}{3}\sum_{t = - \infty}^{\infty}{x\left\lbrack t \right\rbrack e^{- jn\text{ωt}}}\text{ }(3.41)$

如果将区间拓展到某一信号有连续的N个值,那么就得出一个更加通用的公式

$A_{n} = \frac{1}{N}\sum_{t = - \infty}^{\infty}{x\left\lbrack t \right\rbrack e^{- jn\text{ωt}}}\text{ }(3.42)$

设

$X\left( e^{\text{jω}} \right) = \sum_{t = - \infty}^{\infty}{x\left\lbrack t \right\rbrack e^{- j\omega t}}\text{}(3.43)$

根据式那么就有

$A_{n} = \frac{1}{N}X\left( e^{\text{jωn}} \right)\ \ \ (3.44)$

将3.44代回式子3.36得到

$x\left\lbrack t \right\rbrack = \frac{1}{N}\sum_{t = - \infty}^{\infty}{X\left( e^{\text{jωn}} \right)e^{\text{jnωt}}}\text{ }(3.45)$

因为 $N = \frac{2\pi}{\omega}$ ,因此上式又可以写为

$x\left\lbrack t \right\rbrack = \frac{1}{2\pi}\sum_{t = - \infty}^{\infty}{X\left( e^{\text{jωn}} \right)e^{\text{jnωt}}}w(3.46)$

随着周期趋近于无穷大， $\omega$ 趋近于无穷小，那么，上式就从累加变成了积分，且因为 $X\left( e^{\text{jω}} \right)e^{\text{jωn}}$ 的周期为2π，且其仅在周期内有值，于是，上式也随之变为了

$x\left\lbrack t \right\rbrack = \frac{1}{2\pi}\int_{0}^{2\pi}{X\left( e^{\text{jω}} \right)e^{\text{jωnt}}\text{dω}}\text{ }(3.46)$

非周期有限长度离散时间傅里叶变换

依据之前章节的推断,傅里叶变换仅能支持周期离散时间的信号样本,要得到周期样本,可以对有限长度的信号样本进行补值:

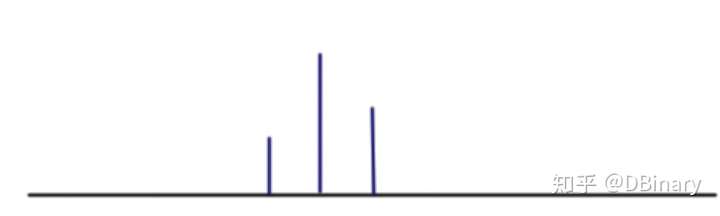图3-6-1 离散时间信号示范

如图3-6-1是一个仅有3个样本的离散时间信号(其中横轴为时间轴),在该信号的其它时间区间,可以假设对取信号进行补值,从而得到一个周期性离散时间信号如图3-6-2是一个对图3-6-1进行补值后的信号，该信号可以使用第四节的变换公式。

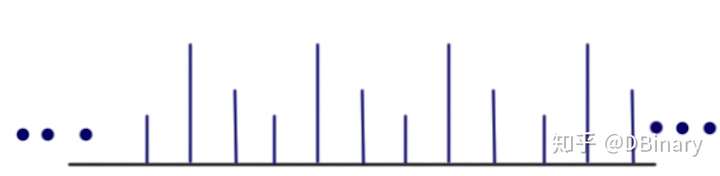图3-6-1 循环补值后的信号

根据第二章第四节的公式3.39及3.36

$A_{n} = \frac{1}{T}\sum_{t = < T >}^{}{x\left\lbrack t \right\rbrack e^{- jn\text{ωt}}}\text{ }(3.39)$

$x\left\lbrack t \right\rbrack = \sum_{t = < T >}^{}{A_{n}e^{\text{jnωt}}}\text{ }(3.36)$

如果将有限长的信号推广到无限长的信号，先假设信号的样本点数为T个，那么，信号x[t]的t取值范围就可以定义在[0,T-1]，因此,将范围限定于[0,T-1]，式3.36可以写成:

$x\left\lbrack t \right\rbrack = \sum_{t = 0}^{T - 1}{A_{n}e^{\text{jn}\omega t}}\text{}(3.47)$

因为 $\omega = \frac{2\pi}{T}$ 因此上式可以写成

$x\left\lbrack t \right\rbrack = \sum_{t = 0}^{T - 1}{A_{n}e^{\text{jn}\frac{2\pi}{T}t}}\text{}(3.48)$

同理,式3.39可以写成

$A_{n} = \frac{1}{T}\sum_{t = 0}^{T - 1}{x\left\lbrack t \right\rbrack e^{- jn\frac{2\pi}{T}t}}\text{ }(3.49)$

依据上式可知,变换的结果也是一个离散的复信号,其范围同样被限定在[0,T-1],在实际的使用中,常常用大写的X[n]来表示变换后的复信号的T倍(即求其频率密度),即

$X\left\lbrack n \right\rbrack = TA_{n}\text{}(3.50)$

那么,3.47就可以写成

$x\left\lbrack t \right\rbrack = \frac{1}{T}\sum_{t = 0}^{T - 1}{X\left\lbrack n \right\rbrack e^{\text{jn}\frac{2\pi}{T}t}}\text{}(3.51)$

3.49可以写成

$X\left\lbrack n \right\rbrack = \sum_{t = 0}^{T - 1}{x\left\lbrack t \right\rbrack e^{- jn\frac{2\pi}{T}t}}\text{}(3.52)$

至此,所有推导完成结束.

*注意,离散福利叶变换的幅度计算和相位计算与傅里叶级数的余弦展开有所不同

依据欧拉公式

$e^{-jwt}=cos(wt)-jsin(wt)$

其实部对应cos虚部对应sin,与傅里叶级数的余弦展开(参考式2.14)+变-号,那么求其相位应该是:

$\varphi = \arctan\left( \frac{b_{n}}{a_{n}} \right)$

同时,依据式3.5,其幅度是

$c_{n}\ \ = \frac{2}{T}\sqrt{{a_{n}}^{2} + {b_{n}}^{2}}$

posted @ 2022-04-18 16:29 Yihoyo 阅读(102) 评论(0) 收藏举报

刷新页面返回顶部

YihoyoのBlog

我没能过上再别人面前昂首挺胸的人生，本以为在笔直奔跑，不知不觉却一身是泥，但只要一直跑下去，泥总会变干脱落