图论学习笔记

图论

图基础

  1. 图的概念：一张图 \(G\) 由若干个点和连接这些点的边构成。称点的集合为 点集 \(V\)，边的集合为 边集 \(E\)，记 \(G=(V,E)\)。

  2. 图的特定名称：

    • 图 \(G\) 的点数 \(|V|\) 称为阶，记作 \(|G|\)。

    • 途径，连接一串节点的边称为序列，如 $ \overrightarrow{puck} $ 就是一条途径。

    • 路径，不经过重复点与重复边的途径称为路径。

    • 回路，有相同头和尾并且不经过重复边的途径称作回路。

    • 环，除了头和尾没有重复边的回路。

    • 重边，端点和方向一样的两条边。

    • 自环，两个端点都是自己的边。

  3. 特殊的图

    • 简单图，不含自环和重边的图。
    • 完全图，完全图的定义是任意两个点之间都有边的无向图，记完全图中点的数量为 \(n\) ，那么 \(n\) 记作那么完全图的边数则为 $C_n^2 = \frac{n!}{2!(n - 2)!} = \frac{n\times (n - 1)}{2} $ 。
    • 有向无环图，不含环的有向图称为有向图无环图，简称 DAG。
    • 树，不含环并且所有点都是联通的图，树是简单图。若干棵树组成的联通块称为森林。

  4. 图的分类方法：

    图的分类有多种方法，但是主要的有两种：

    • 无向图和有向图，无向图的定义为 \(e\in E\) 没有方向，那么称为无向图记作 \(e = (a,b)\)；若 \(e \in E\) 有方向，这时候我们就需要使用向量来表示边的方向了记作 $ \overrightarrow{ab} \(， 当然也可以特别的认为\)\text{无向图}\in\text{有向图}$，因为无向边 \(e = (a,b)\) 等价于 $\overrightarrow{ab}, \overleftarrow{ab} $ 。
    • 稠密图与稀疏图，稠密图的定义就是 \(|E|\) 接近于完全图的边数的图，否则就为稀疏图。

  5. 约定

    • 一般记 \(n\) 表示点集的大小 \(|V|\)，\(m\) 表示边集大小 \(|E|\)。

图的储存方法

邻接矩阵：

直接使用数组储存，\(dis_{i,j}\) 表示 \(i\) 到 \(j\) 的距离。

（1）直观、简单、好理解

（2）方便检查任意一对定点间是否存在边

（3）方便找任一顶点的所有“邻接点”（有边直接相连的顶点）

（4）方便计算任一顶点的度

邻接矩阵的局限性：时间复杂度 \(O(n^2)\) ，空间复杂度 \(O(n^2)\)

（1）浪费空间。对于稠密图还是很合算的，但是对于稀疏图有大量无效元素。

（2）浪费时间。要确定图中有多少条边，则必须按行、按列对每个元素进行检测，所花费的时间代价很大。

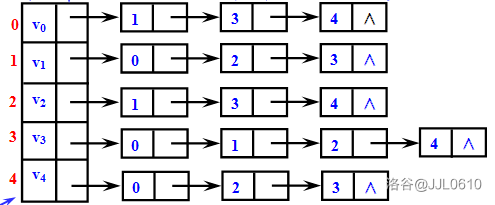
邻接表：

（1）邻接表表示不唯一。这是因为在每个顶点对应的单链表中，各边节点的链接次序可以是任意的，取决于建立邻接表的算法以及边的输入次序。

（2）对于有 \(n\) 个顶点和 \(m\) 条边的无向图，其邻接表有 \(n\) 个顶点节点和 \(2 \times m\) 个边节点。显然，在总的边数小于 \(n(n - 1)\div 2\) 的情况下，邻接表比邻接矩阵要节省空间。

  1. 链式前向星，使用链表记录两点之间距离。

    struct edge{
    int to, next, dis;//这条边所到达的点，这条边的下一条边，这条边的权值
}e[M << 1];//无向图开双倍，有向图一倍就可以了
int head[N], tot;//记录第一条边，现在已经记录几条边了

void add(int from, int to, int dis){//增边
    e[++tot] = edge{to, head[from], dis};
    head[from] = tot;
}   

for(int i = head[x];i;i = e[i].next)//枚举每条边

    2.当然我们也可以使用 vector 动态数组，动态开点，也可以免去浪费空间的麻烦。

    vector<edge>s[];
for(i~n){
	int u = read(), v = read(), d = read()...;
	s[].push(edge{...})
}

图上 DFS 与 BFS

邻接矩阵的搜索的时间复杂度为 \(O(n^2)\)，使用邻接表则为 \(O(n + m)\)。

DFS

DFS使用递归实现的，同时有两种重要的操作——搜索和回溯。

bool vis[];
void dfs(现在已经达到的点){
	for(查找这个点链接的边){
        /*
        dis[] = min(dis[] + 1);
        if(vis[])conitnue;
        vis[] = 1;
        */
		dfs(查找的点, 答案累加);	
        /*
        vis[] = 0;
        */
        \\回溯
	}
}

BFS

BFS使用队列实现，满足优先级。

void bfs(){
	//初始化
	dis[i] = 0;
	while(判定队列非空){
		int fq = 队列头;
		for(查找链接的边){
			记录答案，并且放入队列
		}
	}
}

特殊的搜索

双端队列BFS

BFS的本质是队列，而队列含有优先级，有先进先出的顺序，所以BFS也是具有优先级的，同时由于需要找的是最短路径，那么优先级就是越小的越先出队，那么，双端队列BFS是如何进行维护优先级的呢？我们可以将需要改变的 \(x\) 放置队尾，而不需要改变的 \(y\) 放置队头，使得队列头的权值一定是比队尾小的。

P4667 BalticOI 2011 Day1] Switch the Lamp On - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

Casper 正在设计电路。有一种正方形的电路元件，在它的两组相对顶点中，有一组会用导线连接起来，另一组则不会。有 \(N\times M\) 个这样的元件，你想将其排列成 \(N\) 行，每行 \(M\) 个。 电源连接到板的左上角。灯连接到板的右下角。只有在电源和灯之间有一条电线连接的情况下，灯才会亮着。为了打开灯，任何数量的电路元件都可以转动 90°（两个方向）。

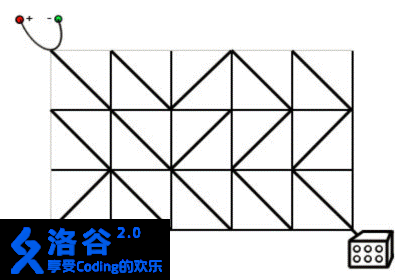
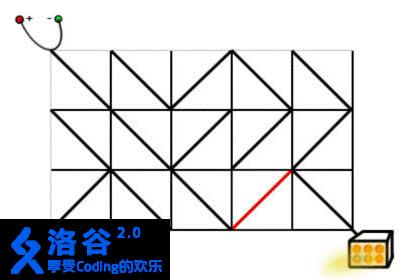
在上面的图片中，灯是关着的。如果右边的第二列的任何一个电路元件被旋转 90°，电源和灯都会连接，灯被打开。现在请你编写一个程序，求出最小需要多少旋转多少电路元件。

思路

我们发现电路只有两种操作——转和不转，可以使用双端队列 BFS，如果需要改变电路的方向我们就把 \(fx,fy\) 放入队尾，否则放入队尾，思路很好想，代码量还是有点的。

AC Code
#include <iostream>
#include <deque>
#include<cstring>
using namespace std;

inline int read(){
	int f = 1,x = 0;
	char ch = getchar();
	while(!isdigit(ch)){
		if(ch == '-')f = -1;
		ch = getchar();
	}
	while(isdigit(ch)){
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}
inline void print(int x){
	if(x > 9)print(x / 10);
	putchar(x % 10 + '0');
}

const int dx[4]={1, -1, -1, 1};
const int dy[4]={1, 1, -1, -1};
const char dc[4]={'\\', '/', '\\', '/'};
const int ix[4]={0, -1, -1, 0};
const int iy[4]={0, 0, -1, -1};

struct edge{
	int x,y;
};
deque<edge> q;
int dis[501][501];
char map[501][501];
int l, c;

void bfs(){
	memset(dis, 0x3f, sizeof(dis));
	q.push_back(edge{0, 0});	
	dis[0][0] = 0;
	while(!q.empty()){
		edge fq = q.front();q.pop_front();
		for(int i = 0;i < 4;i++){
			int fx = fq.x + dx[i], fy = fq.y + dy[i];
			int jx = fq.x + ix[i], jy = fq.y + iy[i];
			if(fx < 0 || fx > l || fy < 0 || fy > c)continue;
			if(dc[i] != map[jx][jy]){
				int d = dis[fq.x][fq.y] + 1;
				if(d < dis[fx][fy]){
					q.push_back(edge{fx, fy});
					dis[fx][fy] = d;
				}
			}else{
				int d = dis[fq.x][fq.y];
				if(d < dis[fx][fy]){
					q.push_front(edge{fx, fy});
					dis[fx][fy] = d;
				}
			}
 		}
	}
	cout << dis[l][c];
}

signed main(){
	l = read(), c = read();
	for(int i = 0;i < l;i++)
		scanf("%s", map[i]);
	if((l + c) & 1)
		puts("NO SOLUTION");
	else 
		bfs();
	return 0;
}

最短路

在研究最短路问题时研究对象是路径而不是途径，因为最短路中一定不会走重复边，否则起点和终点之间存在负环，最短路不存在。

  • 带权图，边附有权值的图称为带权图。所有边非负的图称为非负权图，都为正数称为正权图。
  • 边权，记作 \(v_e\) 或 \(v_{a,b}\)，默认为 \(1\) 。
  • 路径长度，路径上每条边的权值之和。
  • 负环，长度为负数的环。
  • 最短路，一张图上，称 \(s\) 到 \(t\) 的最短路为连接 \(s\) 到 \(t\) 的路径。若不存在这样的路径（不联通或无法到达），或者最小值不存在（存在可经过负环），最短路不存在。

Part 1 全源最短路

Floyd

Floyd 的主要思想 dp，时间复杂度 \(O(n^3)\)

很容易理解，可以想象成一中校门口离机房的最短路就等于 \(\min(\text{门口到操场再到机房的距离},\text{门口到食堂再到机房的距离},\text{门口直接到机房的距离})\)

设 \(dis_{k,i,j}\) 表示 \(s\) 到 \(t\) 的路径只经过了编号 \(\le k\) 的点的最短路，从 \(dis_{k,i,j} → dis_{k + 1,i,j}\) 只需要添加 \(k + 1\) ，那么就可以枚举 \(i\) 和 \(j\) ，即使用 \(dis_{k, i, k + 1} + dis_{k, k + 1,j}\) 更新 \(dis_{k,i,j}\)。

同时，根据状态转移方程可知，可以降维，得到状态转移方程 \(dis_{i,j} = \min(dis_{i,k} + dis_{k,j})\)。

for(int k = 1;k <= n;k++)
	for(int i = 1;i <= n;i++)
		for(int j = 1;j <= n;j++)
            dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
传递闭包

传递闭包可以使用 Floyd 实现。

B3611 【模板】传递闭包 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

给定一张点数为 \(n\) 的有向图的邻接矩阵，图中不包含自环，求该有向图的传递闭包。

一张图的邻接矩阵定义为一个 \(n\times n\) 的矩阵 \(A=(a_{ij})_{n\times n}\)，其中

\[ a_{ij}=\left\{ \begin{aligned} 1,i\ 到\ j\ 存在直接连边\\ 0,i\ 到\ j\ 没有直接连边 \\ \end{aligned} \right.\]

一张图的传递闭包定义为一个 \(n\times n\) 的矩阵 \(B=(b_{ij})_{n\times n}\)，其中

\[ b_{ij}=\left\{ \begin{aligned} 1,i\ 可以直接或间接到达\ j\\ 0,i\ 无法直接或间接到达\ j\\ \end{aligned} \right.\]

其实，判断 \(b_{i,j}\) 可以看做图中有没有一条 \(i\) 到 \(j\) 的路径，也就是看 \(dis_{i,j}\) 是否不为 \(\inf\) ，不为 \(\inf\) 的前提就是 $dis_{i,k} \neq \inf $ 并且 \(dis_{k,j} \neq \inf\) 那么我们就可以看做是一个 bool 类型的 Floyd，那么 \(f_{i,j} = f_{i,j}\cup (f_{i,k} \cap f_{k,j})\)。

注： \(\cup\) 表示 | ，\(\cap\) 表示 &。

for(int i = 1;i <= n;i++)
	for(int j = 1;j <= n;j++)
		for(int k = 1;k <= n;k++)
			f[j][k] |= f[j][i] & f[i][k];

上述代码时间复杂度 \(O(n^3)\)，可以使用 bitset 优化至 \(\frac{n^3}{w}\)

for(int i = 1;i <= n;i++)
	for(int j = 1;j <= n;j++)
		if(a[i][j])
			a[i] |= a[j];

Part 2 单源最短路

Bellman-Ford

称松弛表示对每条边 \((a,b)\)，用 \(dis_a + v_{a,b}\) 更新 \(dis_b\) ，最多更新 \(n - 1\) 轮

Bellman-Ford 可以判断是否有负环，如果在松弛了 \(n-1\) 轮时，仍然可以更新最短路，说明存在负环。

void BellmanFord(){
    memset(dis,INF,sizeof(dis));
    dis[1] = 0;
    for (int i = 1;i <= n;i++){//枚举 n - 1 次，这里判负环所以枚举 n 次
        check = 0;
		for (int j = 1; i <= m; i++){//枚举每一条边
			if (dis[v[j]] > dis[u[j]] + w[j]){
                check = 1;
				dis[v[j]] = dis[u[j]] + w[j];
        	}
        }
        if(!check){
            break;
		}
        if(i == n && check){
            \\存在负环
		}
    }
}
Dijkstra

主要思想贪心，适用于非负权图。

称拓展结点 \(a\) 表示对 \(a\) 的所有临边 \((a,b)\) ，用 \(dis_a + v_{a,b}\) 更新 \(dis_b\) 。

在 \(dis_u = D_u\) 的结点中，取出 \(dis\) 最小的且未被拓展的点并拓展。因为权值非负，所以最短路长度单调不减。

取出 \(dis\) 最小的结点的过程可以使用 priority_queue 维护。拓展 \(a\) 点时，若 \(dis_a + v_{a,b} < dis_b\) 则把 \(dis_b\) 与 \(b\) 的其他信息放入队列。

现在有三个点与三条边将三个点都连接起来了这时：

dis1 dis2 dis3
0 5 10

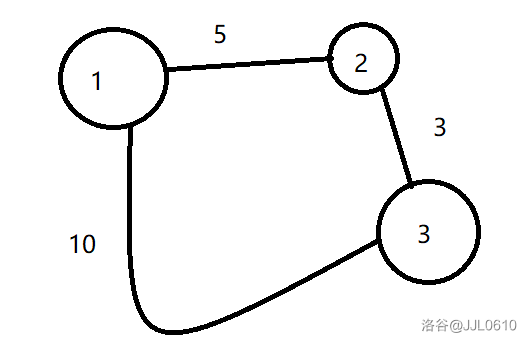
\(1\) 会先找到 \(2\) 然后，对 \(2\) 进行操作，则路径就会变成这样，由于走一条弯路比走两条路远远多走，那么我们还不如直接删除那条长的路，留下短的路。

dis1 dis2 dis3
0 5 8

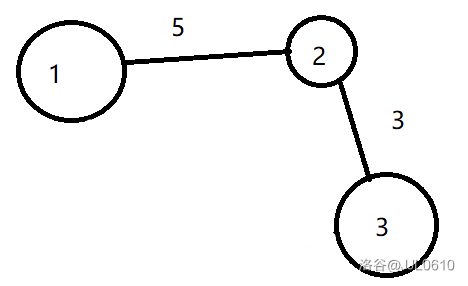
代码实现：

暴力

\(O(n ^ 2 + m)\)

for(int i = 1;i <= n;i++){
	u = -1; minn = INT_MAX;
	for(int v = 1;v <= n;v++)
		if(!vis[v] && dis[v] < minn)
			minn = dis[v], u = v;
	if(u == -1)break;
	else vis[u] = 1;
	for(auto i : a[u]){
		dis[i.to] = min(dis[i.to], dis[u] + i.v);
	}
}
堆优化

\(O(m \log m)\)

void dijkstra(){
	for(int i = 1;i <= n;i++)
		dis[i] = 0x7fffffff;
	dis[s] = 0;
	q.push(edge{0, s});
	while(!q.empty()){
		int now = q.top().e;q.pop();
		if(vis[now])continue;
        vis[now] = 1;
        for(int i = head[now];i;i = e[i].next){
        	int to = e[i].to, d = e[i].dis;
        	if(dis[to] > dis[now] + d){
        		dis[to] = dis[now] + d;
        		q.push(edge{dis[to], to});
			}
		}
	}
}

在 \(m\) 到达 \(n ^ 2\) 级别时，暴力比堆优化快。

U329302 最美相遇（无数据） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

定义两人『最美的相遇』，为两人相遇时间最少的相遇。现在 JJL 希望找到他与每人『最美的相遇』。

我们规定相遇共有 \(2\) 种方式：

  1. 直接的相遇——顾名思义，就是 JJL 直接找到 A。
  2. 间接的相遇——JJL 认识了 B，然后 B 认识了 A，B 再将 A 介绍给了 JJL。

显然，每个人的速度可能不会完全相同，即存在 A 与 B 的相遇距离与 A 与 C 的相遇距离相等，但 A 与 B 的相遇时间与 A 和 C 的相遇时间还是有可能不同。

在 JJL 的『最美的相遇』有 \(n\) 个点，在这 \(n\) 个点中，每两个点都有一条无向边，每条边的权值 \(len_i\) 代表 A 与 B 的直接相遇距离，同时每个点都有 \(1\) 个速度 \(s_j\)。

当然，请注意：人是专一的，在 A 和 JJL 相遇的时候，A 就无法去找 B。

请找到 JJL 与 \(n\) 个点中每个点的『最美的相遇』。若 JJL 不可能与 \(i\) 相遇，输出 Impossible。

模板

本题其实很水，于最短路不同的只有 \(time_i = len_{i,j} \div (speed_i + speed_j)\) 然后再跑一边 Dijkstra 就可以了。

SPFA

众所周知 SPFA 已经死了，就是因为下面这个菊花图，可以直接卡掉 SPFA。

但是由于 Dijkstra 无法处理负权图，所以还是需要学习 SPFA。

SPFA 是 Bellman-Ford 的队列优化，松弛点 \(x\) 时找到接下来可能松弛的点，及于 \(x\) 相邻且最短路被更新的点放入队列。

#include <bits/stdc++.h>
using namespace std;

inline int read(){
	int f = 1,x = 0;
	char ch = getchar();
	while(!isdigit(ch)){
		if(ch == '-')f = -1;
		ch = getchar();
	}
	while(isdigit(ch)){
		x = (x << 1) + (x << 3) + (ch ^ 48);
		ch = getchar();
	}
	return x * f;
}
inline void print(int x){
	if(x > 9)print(x / 10);
	putchar(x % 10 + '0');
}

struct edge{
    int to, next, dis;
}e[5210];
int head[510], tot;

void add(int from, int to, int dis){
    e[++tot] = edge{to, head[from], dis};
    head[from] = tot;
}   

int dis[510], cnt[510], n;
bool vis[510];

bool spfa(){
    memset(dis, 63, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    memset(cnt, 0, sizeof(cnt));
    dis[2] = 0;
    queue<int> q;
    q.push(2);
    while(!q.empty()){
        int fq = q.front();
        vis[fq] = 0,q.pop();
        for(int i = head[fq];i;i = e[i].next){
            int to = e[i].to, d = e[i].dis;
            if(dis[to] > dis[fq] + d){
                dis[to] = dis[fq] + d;
                cnt[to] = cnt[fq] + 1;
                if(cnt[to] >= n)return 1;
                if(!vis[to]){
                    vis[to] = 1;
                    q.push(to);
                }
            }
        }
    }
    return 0;
}

int main() {
    int T = read();
    while(T--){
        tot = 0;
        memset(head, 0, sizeof(head));
        n = read();
        int m = read(), w = read();
        for(int i = 1;i <= m;i++){
            int u = read(), v = read(), p = read();
            add(u, v, p);
            add(v, u, p);
        }
        for(int i = 1;i <= w;i++){
            int u = read(), v = read(), p = read();
            add(u, v, -p);
        }
        cout << (spfa() ? "YES" : "NO") << endl;
    }
	return 0;
}

……连载中

posted @ 2023-08-17 16:59  Light_starup  阅读(134)  评论(2)    收藏  举报