DP

DP 心得总结

DP 初步

dp 难在思考，状态转移方程最为重要，我们要认真思考，将整个思路变为状态转移方程。

背包

最简单的 dp ，要知道背包的状态，背包中所存储，背包中的空间的缩小也是很重要的，我们也要尽量把多维缩小，优化时间复杂度可以更好的实现代码。

状态：

1. 代价等于价值，我们可以直接设置 \(dp_i\) 表示价值 \(i\) 也表示价值，如P2392 kkksc03考前临时抱佛脚。

2. 代价为状态，\(dp_i\) 表示通过 \(i\) 的代价得到的最大价值，如P1048 [NOIP2005 普及组] 采药。

背包分类：

1. 01背包，选还是不选。P1048 [NOIP2005 普及组] 采药
2. 完全背包，可以无限选择。P1616 疯狂的采药
3. 多重背包，可以选多个。P1833 樱花
4. 分组背包，一个组里只能选一个。P1757 通天之分组背包
5. 有依赖背包，两种物品一定要一起选择。P1064 [NOIP2006 提高组] 金明的预算方案
6. 混合背包，将上面的混合。P2851 [USACO06DEC] The Fewest Coins G

优化：

1. 滚动数组，如果 \(dp_{i,j}\) 的状态只和上一行有关，我们就可以使用滚动数组。
2. 如果状态具有单调性，那么我们就可以优化为 \(1\) 维数组。
3. 多重背包 二进制优化，不难证明有了在 \([1,n)(n|2)\) 所有 \(2\) 的幂，我们就可以得到所有 \(\le n\) 的数。

状压dp

状压 dp 容易实现，难在状态转移方程，要想实现状压 dp 我们先要会位运算。

之后我们就可以把一个 bool 类型的 \(01\) 串压为一个二进制的数，这样就可以储存在数组中。

如 \(i = 10\) 时可以表示 \(1010\)，也就是选取了第 \(4\) 个和第 \(2\) 个。

状态：\(dp_{i,j}\) 总是表示在选取了 \(i\) 方案之后留下 \(j\) 所得到的最大价值。

方程：\(dp_i = max(dp_{i ⊕ 1 << k}+v_{k,j})\)

区间 dp

区间 dp 是用来求一段区间中操作最大值的，主要思想就是大的区间化为小的区间。

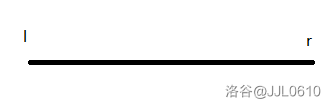
若我们要求上面 \([l,r]\) 的操作最大值，我们可以这么求。

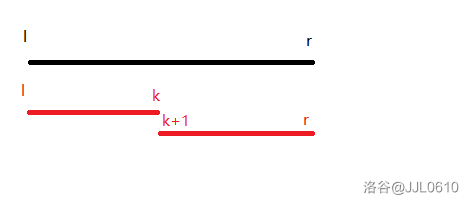
先求出 \([l,k]\) 和 \([k + 1,r]\) 一步一步分解，最后就可以分解成最小的已知的值。

这样就可以得到 \([l,r]\) 的值。

状态：\(dp_{i,j}\) 通常表示 \([i,j]\) 中的操作最大值。

方程：\(dp_{i,j} = \max(dp_{i,k} + dp_{k + 1,j} + v_{i,j})\)

add-2023.10.13

好久没有碰 dp 了，复习一下，并且增加 树形 dp。

树形 dp

顾名思义，树形 dp 是一种在树上进行 dp 的操作，别看要用到树，其实树形 dp 的状态转移方程是最容易想的。

例题

题目描述

树上每个点会让自己到 \(N(\text{包含自己})\) 个点的路径之上的所有的结点的权值 \(+1\)，请求出树上每一个点的权值。

题目分析

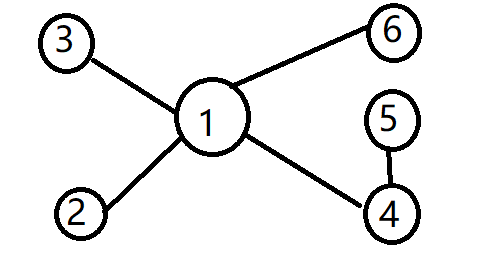
在这样的一棵树中节点 \(1\) 的权值应该是 \(2(1,2) \times 3(4,5,6) + 5(2,3,4,5,6) + \sum{d[root(x)] * }\)