你说得对,但是我怎么没学过后缀科技啊???
后缀数组 (SA)
后缀数组(SA,Suffix Array)最基础的应用是,可以将给定串 \(S\) 的所有后缀串排序。
一点定义:\(sa_i\) 表示第 \(i\) 小的后缀的编号,\(rk_i\) 表示后缀 \([i,n]\) 的排名。显然 \(sa_{rk[i]}=rk_{sa[i]}=i\)。
后缀数组就是 \(sa\) 数组,我们可以利用后缀排序(SS,Suffix Sort)求出后缀数组。
\(\text{ }\)
⭐ 后缀排序
首先 \(O(N^2\log N)\) 的做法是平凡的。
我们考虑优化暴力。我们先比较第一位,肯定能把所有后缀分成若干组。这个时候,暴力做法就是直接去比较第二位,但是第 \(2\) 位刚才已经比较过了!我们用某种方法按前两位分好组,发现第 \(3,4\) 位也应当比较过了。以此类推,我们发现过程类似一个倍增。这也就是后缀排序的大致思想了——利用倍增,只需要进行 \(O(\log N)\) 次分组操作。
稍微整合一下流程:
- 依照前 \(1\) 位排名。直接把字符对应成编号即可。
- 依照前 \(2\) 位排名。将 \((rk_i,rk_{i+1})\) 进行双关键字排序,更新 \(sa\) 数组,并重标号 \(rk\) 数组。此时 \(rk_i\) 记录 \([i,i+1]\)。
- 依照前 \(4\) 位排名。将 \((rk_i,rk_{i+2})\) 进行双关键字排序,恰好对应了 \([i,i+1]\cup[i+2,i+3]=[i,i+3]\)。更新 \(sa,rk\) 数组。此时 \(rk_i\) 记录 \([i,i+3]\)。
- 同样道理,不断倍增 \(k\),每次依照前 \(k\) 位排名。将 \((rk_i,rk_{i+k/2})\) 进行双关键字排序,恰好对应了 \([i,i+k/2-1]\cup[i+k/2,i+k-1]=[i,i+k-1]\)。更新 \(sa,rk\) 数组。此时 \(rk_i\) 记录 \([i,i+k-1]\)。
- 当 \(k\ge n\) 时,所得到的 \(sa\) 就是我们的后缀数组。
下面是从洛谷题解盗过来的图。
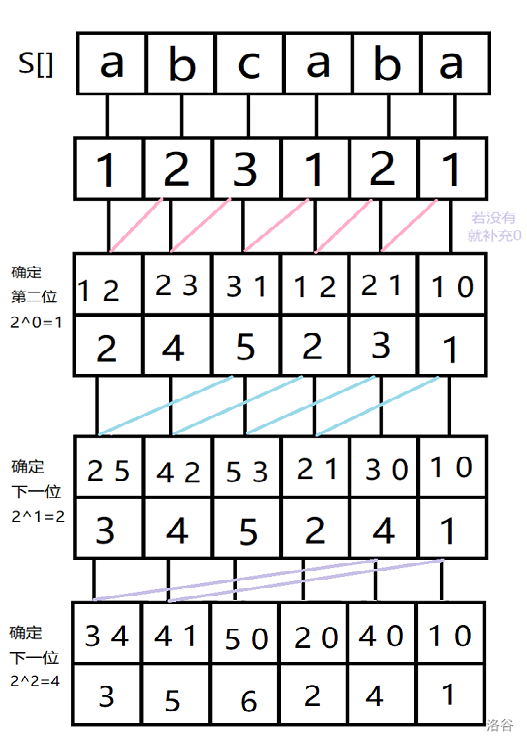
模拟上述过程做到 \(O(N\log^2 N)\)。注意双倍空间。代码相当好写:
void SuffixSort() {
for (int i = 1; i <= n; i++) sa[i] = i, rk[i] = s[i - 1];
for (int k = 1; k <= n; k <<= 1) {
sort(sa + 1, sa + n + 1, [&](int x, int y) {return rk[x] != rk[y] ? rk[x] < rk[y] : rk[x + k] < rk[y + k];});
for (int i = 1, idx = 0; i <= n; i++) _rk[sa[i]] = (rk[sa[i - 1]] == rk[sa[i]] && rk[sa[i - 1] + k] == rk[sa[i] + k] ? idx : ++idx);
for (int i = 1; i <= n; i++) rk[i] = _rk[i];
}
}
注意到值域 \(O(N)\),将 std::sort 改为计数排序做到 \(O(N\log N)\)。
下面代码还加入了点常数优化(参考 OI-Wiki 对应页面):
- 第二关键字无需计数排序,因为你上一轮排好了啊。把 \(sa_i+k>n\) 的放前面,其他顺序放后面即可。
- 提前退出。如果发现 \(idx=n\) 说明已经排好了,直接跳车即可。
void srt() {
for (int i = 1; i <= idx; i++) cnt[i] = 0;
for (int i = 1; i <= n; i++) cnt[rk[i]]++;
for (int i = 1; i <= idx; i++) cnt[i] += cnt[i - 1];
for (int i = n; i; i--) _sa[cnt[rk[sa[i]]]--] = sa[i];
for (int i = 1; i <= n; i++) sa[i] = _sa[i];
}
void SuffixSort() {
for (int i = 1; i <= n; i++) sa[i] = i, rk[i] = s[i - 1];
idx = 128, srt();
for (int k = 1; k <= n; k <<= 1) {
int cur = 0; for (int i = n - k + 1; i <= n; i++) _sa[++cur] = i;
for (int i = 1; i <= n; i++) if (sa[i] > k) _sa[++cur] = sa[i] - k;
for (int i = 1; i <= n; i++) sa[i] = _sa[i];
srt();
idx = 0; for (int i = 1; i <= n; i++) _rk[sa[i]] = (rk[sa[i - 1]] == rk[sa[i]] && rk[sa[i - 1] + k] == rk[sa[i] + k] ? idx : ++idx);
for (int i = 1; i <= n; i++) rk[i] = _rk[i]; if (idx == n) break;
}
}
前者洛谷跑 3.67s,后者跑 560ms,一目了然。
线性科技我不会。
\(\text{ }\)
⭐ LCP 与 height 数组
定义后缀数组上的函数 \(\operatorname{LCP}(i,j)=\operatorname{lcp}(sa_i,sa_j)\),即两后缀的最长公共前缀。
下面是它的一些显然的性质:
- \(\operatorname{LCP}(i,j)=\operatorname{LCP}(j,i)\)。
- \(\operatorname{LCP}(i,i)=n-sa_i+1\)。
- 对于 \(\forall i\le k\le j,\operatorname{LCP}(i,j)=\min(\operatorname{LCP}(i,k),\operatorname{LCP}(k,j))\)。
- 推论:\(\operatorname{LCP}(i,j)=\min\limits_{k=i+1}^{j}\operatorname{LCP}(k-1,k) \triangleq\min\limits_{k=i+1}^{j}h_k\)。
依据性质 \(4\),于是只需要求出 \(\color{red}h_i=\operatorname{LCP}(i-1,i)\)。这个就是 height 数组了。
我们只需要利用一条关键性质,就能完成线性求解 height 数组!
\(\textbf{Lemma. }\)
\[\forall i\ge2, h[rk_i]\ge h[rk_{i-1}]-1 \]\(\textbf{Proof.}\)
若 \(h[rk_{i-1}]=0\) 显然成立,下文讨论 \(\operatorname{LCP}\) 至少为 \(1\) 的情况。
由定义,\(h[rk_{i-1}]=\operatorname{LCP}(i-1,sa[rk_{i-1}-1])\triangleq\operatorname{LCP}(i-1,p)\),把两后缀的第一个字符抹去,得到 \(h[rk_{i-1}]-1=\operatorname{LCP}(i,p+1)\)。于是只需证明 \(h_i\ge\operatorname{LCP}(i,p+1)\),而这是显然的呀,因为 "\([i,n]\) 和它前一位的 LCP" 肯定比 "\([i,n]\) 和它前 \(114514\) 位的 LCP" 要大。\(\square\)
于是直接暴力,均摊复杂度线性。可以参考代码:
for (int i = 1, p = 0; i <= n; i++) {
if (p) p--; while (s[sa[rk[i]] + p] == s[sa[rk[i] - 1] + p]) p++;
h[rk[i]] = p;
}
\(\text{ }\)
任意两后缀 LCP
依据上文,求出 height 数组后转化为 RMQ 问题,单次询问做到 \(O(1)\)。
\(\text{ }\)
循环串排序
将原串 \(S\) 复制一遍在后面,对 \(T=S+S\) 后缀排序,稍微处理下输出即可。\(O(\text{SA}+n)\)
\(\text{ }\)
字符串子串比大小
子串是诈骗的,可以直接比后缀,求出 height 数组,只需要特判 \(\operatorname{LCP}(L_1,L_2)\ge\min(R_1-L_1+1,R_2-L_2+1)\) 时比较两子串长度。否则直接比 \(rk\) 数组即可。单次询问做到 \(O(1)\),比二分哈希强。
小应用,这个直接 \(S+(\neg S)\) 后缀排序,只比 \(rk\) 就够了,不用写 height。
\(\text{ }\)
不同子串个数
考虑 \(\dfrac{n(n+1)}2\) 减重复部分。注意到子串是后缀的前缀,后缀排序后,每个串与前一个串的公共前缀都是多算的(注意这实质是将每个重复子串在左端点去除贡献)。于是答案即 \(\dfrac{n(n+1)}2-\sum h_i\)。\(O(\text{SA}+n)\)
\(\text{ }\)
最长公共子串
子串是后缀的前缀,对 \(S+\textbf{#}+T\) 后缀排序,根据 LCP 理论,只需要在相邻两后缀中找到最大的 LCP,同时满足两后缀恰好一个在 \(S\) 一个在 \(T\)。求出 height 数组后不难实现。\(O(\text{SA}+n)\)
\(\text{ }\)
多个串的最长公共子串
类似上题,对 \((S_1+\textbf{#}+S_2+\textbf{#}+\cdots+\textbf{#}+S_k)\) 后缀排序,并对对应后缀标记所处串,相当于要找到一个区间 \([l,r]\) 满足出现过所有串,且 \(\min\limits_{l<i\le r} h_i\) 最大。双指针 + ST 表做到 \(O(\text{SA}+n\log n)\)。
\(\text{ }\)
出现至少 k 次的子串的最大长度
子串是后缀的前缀,相当于原串后缀排序后有至少 \(k\) 个连续后缀都包含这个子串作为前缀。所以求个 height 数组,每相邻 \(k-1\) 个 height 的最小值再全部取 max,滑动窗口解决。\(O(\text{SA}+n)\)
弱化:BZOJ5673,\(k=2\),输出 height 数组的最大值即可。
\(\text{ }\)
\(\text{ }\)
Reference
SA 部分:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号