导数

给自己看的，随便记点。

1. 导数的定义

先来看一道物理题：

有一辆匀加速直线运动的小车，它在第 \(x\) 秒的速度是 \(x^2\text{ m/s}\)。求小车在某一个时刻的瞬时速度。
瞬时速度的定义

通过翻百度百科，我们得知，计算瞬时速度，只需计算某一段时间的平均速度，计算 \(\Delta t\to 0\) 时的值即可。

这个问题相当简单，计算小车在第 \(x_0\) 秒开始，行走 \(\Delta t\) 的时间，我们有

\[\begin{aligned}v = \dfrac st & = \dfrac{(x_0+\Delta t)^2-x_0^2}{\Delta t}\\ & = \dfrac{2x_0\Delta t+(\Delta t)^2}{\Delta t}\\ & = 2x_0+\Delta t \end{aligned}\]

于是有小车在 \(x_0\) 秒时的瞬时速度

\[v_{0}=\lim_{\Delta t\to0} v=2x_0 \]

现在你已经解决了这个问题。你开始思考这个题在数学上的应用。

我们考虑将其用数学语言描述。

• 小车的速度可以抽象为函数 \(f(x)\)。此例中，\(f(x)=x^2\)。
• 平均速度可以抽象为平均变化率 \(\dfrac{\Delta y}{\Delta x}=\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\)。此例中，\(\dfrac{\Delta y}{\Delta x}=2x+\Delta x\)。
• 于是瞬时速度可以抽象为 \(\lim\limits_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\)。

注意到瞬时速度没有一个名词表述。数学家们直接给了它一个名词：导数。

导数的定义
设 \(y=f(x)\) 在 \(x_0\) 及其附近有意义，如果 \(\lim\limits_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\) 存在，则称 \(f^{\prime}(x_0)=\lim\limits_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\) 为函数 \(y=f(x)\) 在 \(x_0\) 处的导数。

事实上，导数是发掘函数性质的重要工具，下文会对导数进行一定分析。

\(\text{ }\)

\(\text{ }\)

2. 常函数、一次函数、二次函数的导数

这一部分作为引入，熟悉导函数的定义。

2.1. 常函数的导数

已知 \(f(x)=114514\)，计算 \(f^{\prime}(x)\)。

解：根据定义直接得出

\[\begin{aligned} f^{\prime}(x) & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\\ & = \lim_{\Delta x\to0}\dfrac{114514-114514}{\Delta x}\\ & = 0 \end{aligned}\]

对此扩展，不难得出，常函数的导数恒为 \(0\)。

\(\text{ }\)

2.2 一次函数的导数

已知 \(f(x)=114x+514\)，计算 \(f^{\prime}(x)\)。

解：根据定义直接得出

\[\begin{aligned} f^{\prime}(x) & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\\ & = \lim_{\Delta x\to0}\dfrac{(114(x+\Delta x)+514)-(114x+514)}{\Delta x}\\ & = \lim_{\Delta x\to0}\dfrac{114\Delta x}{\Delta x}\\ & = 114 \end{aligned}\]

对此扩展，不难得出，形如 \(f(x)=ax+b\ (a\ne0)\) 的一次函数的导数 \(f^\prime(x)=a\)。

\(\text{ }\)

2.3 二次函数的导数

已知 \(f(x)=11x^2+45x+14\)，计算 \(f^{\prime}(x)\)。

解：根据定义直接得出

\[\begin{aligned} f^{\prime}(x) & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\\ & = \lim_{\Delta x\to0}\dfrac{(11(x+\Delta x)^2+45(x+\Delta x)+14)-(11x^2+45x+14)}{\Delta x}\\ & = \lim_{\Delta x\to0}\dfrac{2\cdot11x\Delta x+11(\Delta x)^2+45\Delta x}{\Delta x}\\ & = \lim_{\Delta x\to0}(22x+11\Delta x+45) \\ & = 22x+45 \end{aligned}\]

对此扩展，不难得出，形如 \(f(x)=ax^2+bx+c\ (a\ne0)\) 的二次函数的导数 \(f^{\prime}(x)=2ax+b\)。

此时已经隐约感觉导数存在运算法则，我们将在后文探讨这个问题。

\(\text{ }\)

\(\text{ }\)

3. 导数的几何意义

导函数终究是函数，其必定存在几何意义。

对于 \(f^{\prime}(x)=\lim_{\Delta x\to0}\dfrac{\Delta y}{\Delta x}\)，我们考察其定义：

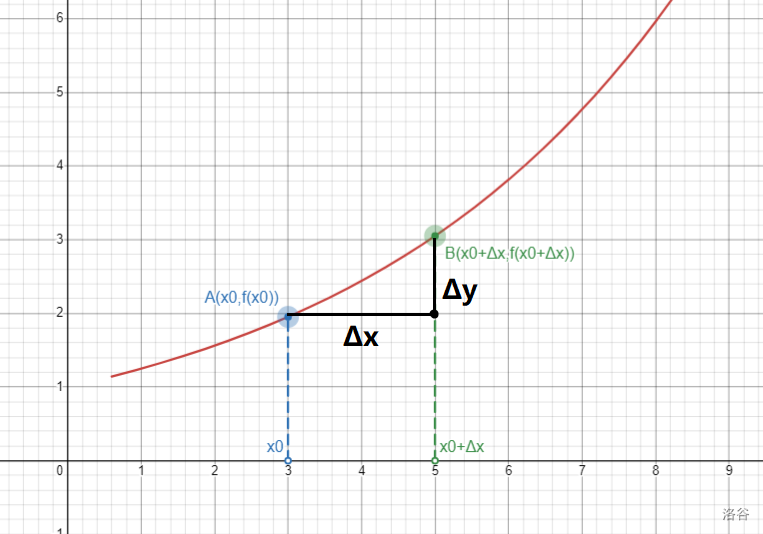
显然，\(\dfrac{\Delta y}{\Delta x}\) 的几何意义就是 \(AB\) 的连线。

加上 \(\lim\) 标记呢？根据 \(\lim\) 的定义与一些观察，发现，导数就是对应点在函数上的切线！

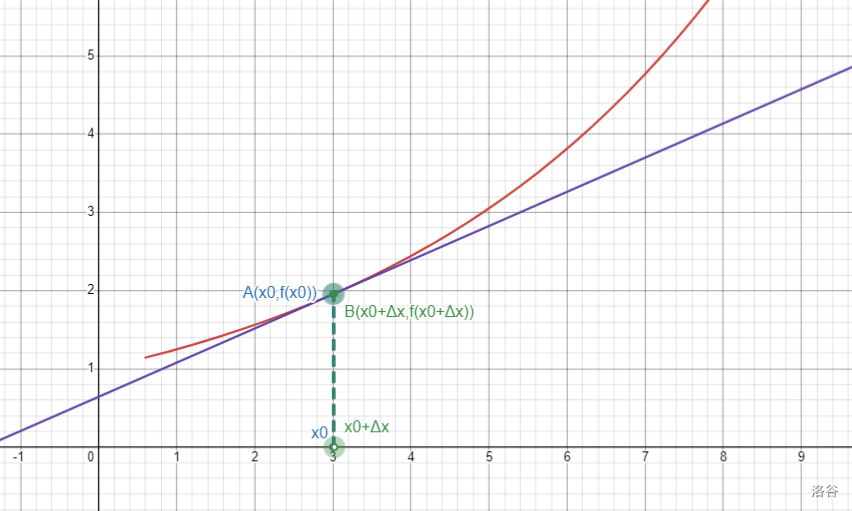
事实上，更严谨的证明需要一些科技，但是我不是 MOer，不管了。

\(\text{ }\)

\(\text{ }\)

4. 一些特殊函数的导数

4.1. 幂函数的导数

事实上，对于函数 \(f(x)=x^k\)，我们有其导函数 \(f^{\prime}(x)=kx^{k-1}\)。

考虑到我是 OIer，因此只对 \(k\in\mathbb{Z}^{+}\) 的情况进行证明。

\[\begin{aligned}f^{\prime}(x) & =\lim_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x} \\ & =\lim_{\Delta x\to0}\dfrac{(x+\Delta x)^k-x^k}{\Delta x} \\ & =\lim_{\Delta x\to0}\dfrac{[\sum\limits_{i=0}^k\binom kix^i(\Delta x)^{k-i}]-x^k}{\Delta x} \\ & =\lim_{\Delta x\to0}\dfrac{\sum\limits_{i=0}^{k-1}\binom kix^i(\Delta x)^{k-i}}{\Delta x} \\ & =\lim_{\Delta x\to0}(\sum\limits_{i=0}^{k-1}\binom kix^i(\Delta x)^{k-i-1}) \\ & =\binom k{k-1}x^{k-1}(\Delta x)^{k-(k-1)-1}) =kx^{k-1} \end{aligned}\]

证毕。

这个性质在多项式中应用广泛。（废话）

\(\text{ }\)

4.2. 三角函数的导数

我就不信信息学竞赛会使用这个东西，摆了。

简单记一下，\((\sin x)^{\prime}=\cos x\)；\((\cos x)^{\prime}=-\sin x\)。\((\tan x)^{\prime}\) 可以利用后文导数的四则运算获得。

\(\text{ }\)

4.3. 指数对数函数的导函数

我们根据一些超过高中范畴的知识，可以得出

\[(e^x)^{\prime}=e^x \]

\[(\ln x)^{\prime}=\dfrac 1x\ (x>0) \]

证明我不会。但是我们不难根据这个，推出任意指数对数函数的导函数：

\[(a^x)^{\prime}=a^x\ln a \ (a>0,a\ne1) \]

\[(\log_a x)^{\prime}=\dfrac1{x\ln a}(a>0,a\ne1,x>0) \]

这一部分的具体证明可以利用后文导数的四则运算获得。

\(\text{ }\)

\(\text{ }\)

5. 函数四则运算的求导法则

这一部分的内容比较有用，可以帮助你快速计算复合函数的导数。

5.1 函数和与差的求导法则

直接给出结论：

\[(f(x)\pm g(x))^{\prime}=f^{\prime}(x)\pm g^{\prime}(x) \]

也可以简记为 \((f\pm g)^{\prime}=f^{\prime}\pm g^{\prime}\)。

证明：对于加法运算，考虑直接按照定义计算，得到

\[\begin{aligned}(f(x)+g(x))^{\prime} & = \lim_{\Delta x\to0}\dfrac{[f(x+\Delta x)+g(x+\Delta x)]-[f(x)+g(x)]}{\Delta x} \\ & = \lim_{\Delta x\to0}\Big(\dfrac{f(x+\Delta x)-f(x)}{\Delta x}+\dfrac{g(x+\Delta x)-g(x)}{\Delta x}\Big) \\ & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}+\lim_{\Delta x\to0}\dfrac{g(x+\Delta x)-g(x)}{\Delta x} \\ & = f^{\prime}(x)+g^{\prime}(x) \end{aligned}\]

P.S. 倒数第二步应用了极限的性质。关于极限的四则运算不在高中范围内，但是可以证明其正确性。

减法同理不难证明。

\(\text{ }\)

5.2 函数积的求导法则

函数积的求导法则会略显诡异：

\[(f(x)\cdot g(x))^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x) \]

可以简记为 \((fg)^{\prime}=f^{\prime}g+fg^{\prime}\)。口诀：前导后不导，后导前不导。

证明：依然考虑直接按照定义计算，得到

\[\begin{aligned}(f(x)g(x))^{\prime} & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)g(x+\Delta x)-f(x)g(x)}{\Delta x} \\ & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)g(x+\Delta x)-f(x+\Delta x)g(x)+f(x+\Delta x)g(x)-f(x)g(x)}{\Delta x} \\ & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)g(x+\Delta x)-f(x+\Delta x)g(x)}{\Delta x}+\lim_{\Delta x\to0}\dfrac{f(x+\Delta x)g(x)-f(x)g(x)}{\Delta x}\\ & = \lim_{\Delta x\to0}\Big(f(x+\Delta x)\cdot\dfrac{g(x+\Delta x)-g(x)}{\Delta x}\Big)+\lim_{\Delta x\to0}\Big(g(x)\cdot\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\Big)\\ & = \lim_{\Delta x\to0}\Big(f(x+\Delta x)g^{\prime}(x)\Big)+\lim_{\Delta x\to0}\Big(g(x)f^{\prime}(x)\Big)\\ & = f(x)g^{\prime}(x)+f^{\prime}(x)g(x) \end{aligned}\]

注意到第二步，巧妙地增补了一项，实质是将 \(f(x+\Delta x)g(x+\Delta x)\to f(x)g(x)\) 拆分为了 \(f(x+\Delta x)g(x+\Delta x)\to f(x+\Delta x)g(x)\to f(x)g(x)\)，也就是将"两个自变量同时变化"拆成"先后变化"。

\(\text{ }\)

5.3 函数商的求导法则

函数商的求导法就更加诡异了：

\[(\dfrac{f(x)}{g(x)})^{\prime}=\dfrac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{g^2(x)} \]

可以简记为 \((\dfrac fg)^{\prime}=\dfrac{f^{\prime}g-fg^{\prime}}{g^2}\)。

证明：还是考虑直接按照定义计算，得到

\[\begin{aligned}(\dfrac{f(x)}{g(x)})^{\prime} & = \lim_{\Delta x\to0}\dfrac{\dfrac{f(x+\Delta x)}{g(x+\Delta x)}-\dfrac{f(x)}{g(x)}}{\Delta x} \\ & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)g(x)-f(x)g(x+\Delta x)}{g(x)g(x+\Delta x)\Delta x} \\ & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)g(x)-f(x)g(x)+f(x)g(x)-f(x)g(x+\Delta x)}{g(x)g(x+\Delta x)\Delta x} \\ & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)g(x)-f(x)g(x)}{g(x)g(x+\Delta x)\Delta x}+\lim_{\Delta x\to0}\dfrac{f(x)g(x)-f(x)g(x+\Delta x)}{g(x)g(x+\Delta x)\Delta x}\\ & = \lim_{\Delta x\to0}\dfrac{f(x+\Delta x)-f(x)}{g(x+\Delta x)\Delta x}+\lim_{\Delta x\to0}\Big(\dfrac{f(x)}{g(x)g(x+\Delta x)}\cdot\dfrac{g(x)-g(x+\Delta x)}{\Delta x}\Big)\\ & = \lim_{\Delta x\to0}\dfrac{f^{\prime}(x)}{g(x+\Delta x)}+\lim_{\Delta x\to0}\dfrac{f(x)\cdot(-1)g^{\prime}(x)}{g(x)g(x+\Delta x)}\\ & = \dfrac{f^{\prime}(x)}{g(x)}-\dfrac{f(x)g^{\prime}(x)}{g^2(x)}\\ & = \dfrac{f^{\prime}(x)g(x)-f(x)g^{\prime}(x)}{g^2(x)} \end{aligned}\]