KMP

qwq。

KMP 是由三个传奇特级生物 Kangaroo、Monkey、Pig 共同发明的算法，她非常聪明，以至于我今天才真正知道他在干什么。

引入

袋鼠猴子小猪 可以线性解决下面的问题：

给定猴子串 \(S\) 与模式串 \(T\)，在 \(S\) 中找到所有与 \(T\) 完全相同的子串。

note：下文记 \(n=|S|,m=|T|\)。

BF（Banana Fly Algorithm）

解决这个问题，我们有一个 BF 算法（即 Banana Fly）算法：

//下标从0开始(string 存储)

void BF() {
	for (int i = 0; i < n; i++) {
		int j = 0;
		for (int ti = i; ti < n && j < m && s[ti] == t[j]; ti++, j++);
		if (j == m) printf("%d\n", i); //s[i,i+m-1] match t
	}
}

KMP - Match

聪明的猴子发现了飞蕉算法的问题：

假如我们把飞蕉算法中，ti 的移动也视为 i 的移动，那么算法的问题是 i 移动了太多次。

为了快速找到香蕉，猴子找来了袋鼠：

袋鼠是什么意思呢？

她的意思是，在 match1 时，我们知道了 \(A=B\)。假如我们用某种方法提前知道了 \(B=C\)，那么在 match2 时，\(j\) 就不用回退那么多，从而加快计算。

于是，我们引入 next[] 数组：\(nxt_i\) 表示，在 \(T_{1,2,\cdots,i}\) 上，最长相同前缀后缀长度。

比如说下面是个例子。

对于串 BABANBABABY，它有 next[] 数组：

• \(next_0\)：对于串 B，\(next_0=0\)。
• \(next_1\)：对于串 BA，\(next_1=0\)。
• \(next_2\)：对于串 BAB，有相同前后缀 B，\(nxt_2=1\)。
• \(next_3\)：对于串 BABA，有相同前后缀 BA，\(next_3=2\)。

类似地，我们有 \(next=\{0, 0, 1, 2, 0, 1, 2, 3, 4, 3, 0\}\)，可以自己手摸以验证。

利用 next[] 数组，我们可以尝试进行匹配了：

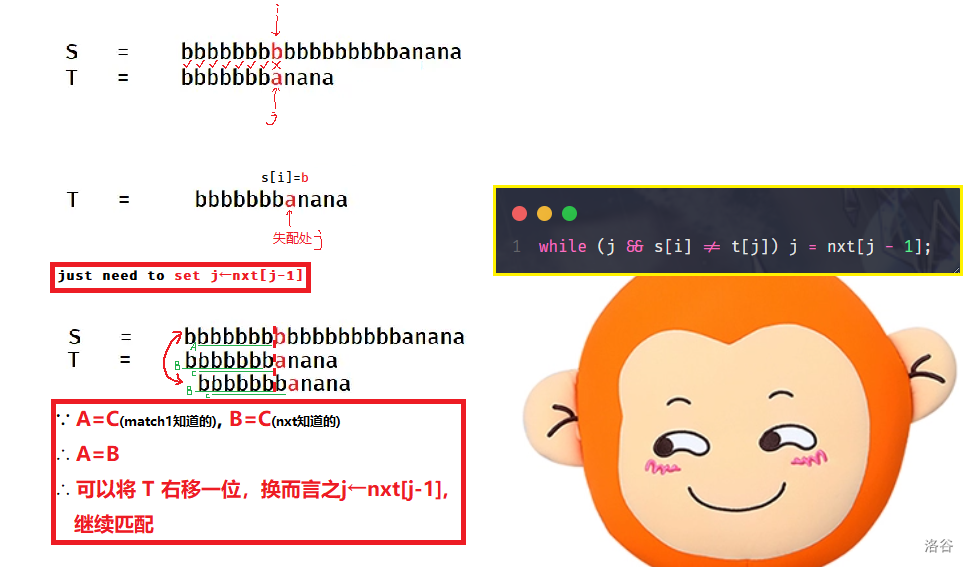
注意到小猴精妙地用 \(j\) 变化表示了 \(T\) 的匹配位置的变化。

换而言之，我们全程只需要不停移动 \(j\)，而 \(i\) 始终不回退。

还是无法理解？下面是另一个例子。

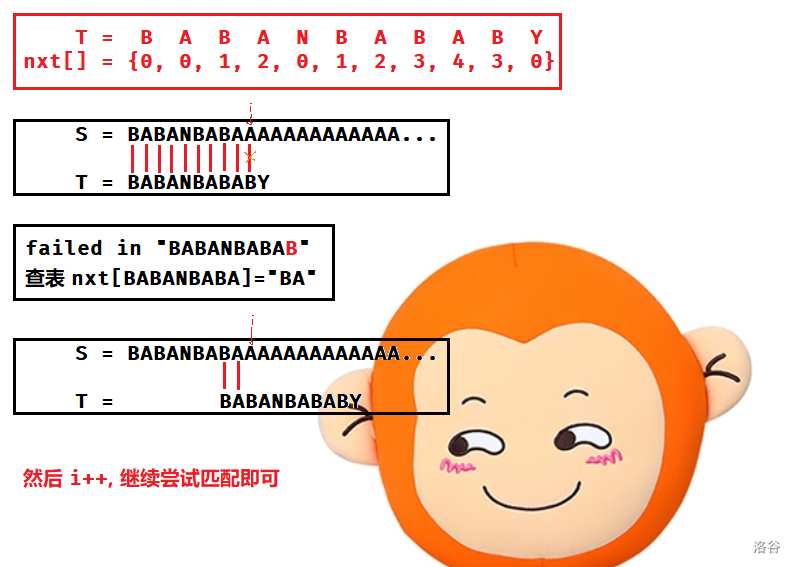
给出这一部分的 code。

void KMP(string s, string t) {
	int n = s.length(), m = t.length();
	for (int i = 0, j = 0; i < n; i++) {
		while (j && s[i] != t[j]) j = nxt[j - 1];    //匹配失败, 回退
		if (s[i] == t[j]) j++;                       //匹配成功
		if (j == m) cout << i - m + 1 << '\n';       //寻找到匹配
	}
}

Time

我们来看看 袋鼠猴子小猪 的时间复杂度。有一些性质：

• j++ 操作只会进行 \(O(n)\) 次（从 Line5 看出）。
• j = next[j - 1] 必定会使 \(j\) 减少至少 \(1\)。

于是，我们不难得出，\(j\) 的减少操作，也只会执行 \(O(n)\) 次。

于是，KMP 算法的复杂度即为 \(O(n+m)\)。

KMP - Next

现在还剩唯一一个问题：next[] 数组怎么求？

实际上，求解 next 数组可以看作自己匹配自己，具体的话可以自己手摸。

（这一部分是小猪负责的，小猪比较懒，所以就不配解释了）

这里放上 code：

int nxt[1000005];
void getnxt(string s) {
	int n = s.length(); nxt[0] = 0;
	for (int i = 1, j = 0; i < n; i++) {
		while (j && s[i] != s[j]) j = nxt[j - 1];
		if (s[i] == s[j]) j++; nxt[i] = j;
	}
}

Code（下标从 1 开始）

将两部分代码组合一下就能完成 KMP 模板。

NOTE：上述代码中混合了 \(nxt_{j-1}\) 与 \(nxt_j\)，在用 KMP 解决实际问题时容易弄混，建议更改成下面的写法：

• 字符串下标从 \(1\) 开始。
• 将 \(nxt_i\) 的定义改成 \(T_{1,2,\cdots,i-1}\) 的最长相同前后缀。

具体可参见下面的代码。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#define mems(x, v) memset(x, v, sizeof x)
#define mcpy(x, y) memcpy(x, y, sizeof x)
using namespace std;
typedef pair <int, int> pii;
typedef long long ll;
typedef unsigned long long ull;
typedef long double wisdom;

int nxt[1000005];
void getnxt(string s, int n) {
	nxt[1] = 0;
	for (int i = 2, j = 0; i <= n; i++) {
		while (j && s[i] != s[j + 1]) j = nxt[j];
		if (s[i] == s[j + 1]) j++; nxt[i] = j;
	}
}
void match(string s, string t, int n, int m) {
	for (int i = 1, j = 0; i <= n; i++) {
		while (j && s[i] != t[j + 1]) j = nxt[j];
		if (s[i] == t[j + 1]) j++;
		if (j == m) cout << i - m + 1 << '\n';
	}
}
int main() {
	ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
	string s, t; cin >> s >> t;
	int n = s.length(), m = t.length();
	s = '%' + s, t = '%' + t;

	getnxt(t, m), match(s, t, n, m);
	for (int i = 1; i <= m; i++) cout << nxt[i] << ' ';
	return 0;
}

袋鼠猴子小猪 实在是太聪明了，我觉得我这一辈子都是比不上袋鼠、猴子与小猪了。

Trick

• 一个串 \(S\) 的最小循环节长度为 \((n-nxt_n)\)。

应用：P4391，P3435，P10475，UVA1328。

• 一个串的所有相同前后缀为 \(nxt_n,nxt_{nxt_n}, nxt_{nxt_{nxt_n}}, \cdots\)。

应用：P2375，P3435。

除此之外，KMP 更多时用在与其他算法结合，真正困难的题目中，要么就是需要对 KMP 的 nxt[] 数组完全理解，要么只是优化复杂度的一部分。