Hey Gift:只有信仰才会经历陪伴每个低谷
P3750 [六省联考 2017] 分手是祝愿
为啥这么奶龙?
考虑 \(50\) 分怎么做:显然从高向低贪心地按即可。因为每次最大的 \(\frac{n}{2}\) 个都是确定要按的,类似分治地正确性十分显然。
对 \(2^{10}\) 个状态进行高斯消元可以通过第一档部分分。
考虑这个贪心说明了什么。我们换一个角度看它的正确性,从大往小扫只是为了免除后效性的影响,实际上就是一个确定的方案,因为异或是没有顺序的。
容易发现每个键都不存在被别的组合键代替的方式。于是这进一步说明,每种状态只恰好有一种方案可以把它归零,我们的目标是随机按键达到该方案的一个大小小于等于 \(k\) 的子集。
先特判掉直接就可以的。
然后显然地,我们发现每次随机按一个键最多导致多按 \(1\) 个键或者少按 \(1\) 个键。所以当现在我们的状态需要按超过 \(k\) 次的时候,我们必然是随机按到大小为 \(k\) 的子集。
于是考虑 \(f_i\) 表示现在还差 \(i\) 个键要按,按到空的期望操作次数。那么:
这样子的式子我们只能模拟高斯消元,非常恶心。考虑换一个状态。
我会期望线性性!考虑 \(f_i\) 表示从还差 \(i\) 个键要按到还差 \(i-1\) 个键的期望操作次数。那么:
式子是好理解的,后面一坨相当于走错了一步导致 \(i\gets i+1\),于是要先用 \(f_{i+1}\) 操作回来,再用 \(f_i\) 操作到 \(i-1\),当然还要算上一开始走过去的那一步。
trickily,进行无穷期望移项即可 dp,答案就是 \(f_1\) 到 \(f_{cnt}\)(\(cnt\) 为初始状态最少操作次数)的和。
值得注意的细节是 \(f\) 的定义域为 \([1,n]\),并非 \([1,cnt]\),因为在走错的过程中我们可能会错得离谱。边界上设置 \(f_{n}=1\) 即可。
记得乘上 \(n!\)。
P3214 [HNOI2011] 卡农
容易想到 xor hashing,这说明我们只需确定前 \(m-1\) 个集合,最后一个集合就是固定的。
于是我们可以先瞎 jb 乱选 \(m-1\) 个,先取答案 \(f_m={{2^n-1}\choose{m-1}}\),然后考虑要容斥什么:
- 最后一个集合剩了个空集。
- 最后一个集合和前面某个集合相同。
考虑第一个就是 \(f_{m-1}\)。
考虑第二个,注意到显然若我们删去相同的两个集合将构成一个 \(m-2\) 处的合法答案。所以这里的所有可能性都可以看成是 \(f_{m-2}\times [2^n-1-(m-2)]\)。
把这两种减掉,我们就得到了选择前 \(m-1\) 个集合使得最后一个集合合法的选法数量。然后考虑无序性,我们无法钦定“最后一个集合”,这显然直接除以 \(m\) 就好了,每一个方案都在每一个做“最后一个集合”时被计算到一次。
于是我们获得了简洁的递推式:
组合数我们预处理一下下降幂就好了。
Codeforces Round 1008 (Div. 1)
顺国国耻。
A. Breach of Faith
条件显然是偶数位等于奇数位。我们只需把原来的一部分当成奇数一部分当成偶数,使得它们的和的差不出现在原来的数里面,这样就能补过去填充集合大小。
一个自然的想法是分成等大的两部分,然后就寄了。
我们跳出思维定势,考虑一部分拿 \(n+1\),一部分拿 \(n-1\)。显然应该让其中一个集合拿最大的 \(n+1\) 个,另一个集合拿最小的 \(n-1\) 个,此时两个集合的和的差可以刻画成至少是 \(\max-\min\) 再加上某两个数的和,这个值必然大于 \(\max\),于是构造出解。
B. Finding OR Sum
想到了没有细想,怎么回事呢?
我们只需确定每一位上 \(x,y\) 的形态即可。
考虑查询所有奇数位和所有偶数位,也就是两个 01 间隔的串。这样做的好处是,我们注意到 \(n=1\) 的位上产生的贡献是非常固定的,我们尝试通过 1 作为间隔独立开了位,避免进位的问题。\(n=1\) 的位上必然会进位,加起来最后又必然是 \(0\),这些信息足以让我们推理出它前后位上的情况。
分类讨论即可。
C. Binary Subsequence Value Sum
考虑在已知 01 串的情况下怎么计算答案。
注意到 \(F\) 的意思其实是 1 的个数减去 0 的个数。自然地,我们给 1 赋权 \(1\),给 0 赋权 \(-1\),然后考虑我们希望两段的和乘积最大。
注意到两段的和是固定的。根据均值不等式,答案会是 \(\left\lfloor\frac{sum^2}{4}\right\rfloor\),\(sum\) 表示整个序列的和。
然后我们开始分类讨论。
- \(1\) 变 \(-1\):
- 所有经过它的 \(sum\le 0\) 的子序列 \(sum\) 减小了 \(2\)。随便搓两个可以发现产生的多出贡献是 \(|sum|+1\)。
- 所有经过它的 \(sum=1\) 的子序列 \(sum\) 减小了 \(2\)。此时贡献没有区别,你也可以理解为减少了 \(sum-1\) 的贡献。
- 所有经过它的 \(sum>1\) 的子序列 \(sum\) 减小了 \(2\)。随便搓两个可以发现产生的减少贡献是 \(sum-1\)。
于是这部分贡献其实就是减去所有子序列的 \(sum\) 之和,然后加上子序列的数量 \(2^{n-1}\)。考虑我们是如何计算所有子序列的 \(sum\) 之和的:除了修改的这一位 \(i\) 的每一位都贡献 \(c_j\times 2^{n-2}\),这一位贡献 \(c_i\times 2^{n-1}\)。考虑因为这里 \(c_i\) 是 \(1\),所以和子序列的数量抵消了。我们只需减去 \(\sum c_j\times 2^{n-2}\)!
\(-1\) 变 \(1\) 是类似的,我们只需加上这个值。
于是考虑如何维护初值。考虑初值形如:
枚举 \(a-b\),然后使用范德蒙德卷积。
处理组合数即可。
E. Another Folding Strip
喜欢折纸对吗?
首先考虑怎么计算一个序列的 \(f\)。考虑你的折纸操作本质上是可以使得哪些位置减 \(1\):可以发现就是一些奇偶相间的位置。
又是类似 01 串的问题!你想到 C 里面你设置了 \(\pm 1\) 的权值来刻画,不妨再用一次。我们把偶数位设置成正数,奇数位取反设置成负数,目标是让整个序列变成全 \(0\)。这样每次选择一个序列都将使得这个序列的总和减小或增大 \(1\)。
然而只判定总和并不能说明整个序列都是 \(0\)。容易想到我们实际上是要让每个前缀和都是 \(0\) 就充要了。我们本质上是在对于选择一些偶数位的前缀和 \(-1\)(同时可以携带它后面的那个奇数位),或者选择一些奇数位的前缀和 \(+1\)(同时可以携带它后面的那个偶数位)。
考虑答案下界:前缀和的最小值必然在奇数位处取得,最大值必然在偶数位处取得,我们需要把这两个东西都拉到 \(0\),所以答案似乎就是最小值的绝对值加最大值的绝对值。下界显然是容易取得的。
注意到最小值必然是非正数,但是最大值并不一定是非负数,比如 9999 1 这种情况。容易发现这种情况我们需要让奇数位把偶数位顺便带走。所以答案应该就只是最小值的绝对值。也可以理解成最大值在 \(0\) 处取得而为 \(0\)。
进一步转化,答案就是前缀和的最大值减前缀和的最小值。对于所有区间求答案的和用任意数据结构都可以维护。
比较漂亮的分析过程。
upd on 2025.6.2:
重新简单写一下这个题。之前感觉理解不太深刻的。
还是考虑怎么快速计算一个序列的 \(f\)。容易发现一次操作等价于使得一个奇偶相间的下标序列 \(-1\)。不妨考虑使得奇数处取反变为 \(+1\),这样我们相当于每次可以做两种操作使得所有前缀和都为 \(0\)(这显然是整个序列为 \(0\) 的等价条件):
- 选择一个奇数位置子序列,前缀和数组加上 \(1\)。显然上述操作可以扩展为这个,我们只需给每个奇数都选上它后面一个偶数就可以规避掉对其他位置前缀和的增加,这样就可以只加奇数位置了。
- 偶数位置同理。
容易发现这两种操作完全覆盖了原操作,所以是等价转化。
然后发现奇数处 \(>0\) 的完全没用,它可以跟着前面那个大于自己的的偶数先做,做到 \(<0\) 在说。偶数处同理。所以我们只需考虑奇数处 \(<0\) 和偶数处 \(>0\) 的部分。
显然这两个部分我们只需考虑奇数位置最小值和偶数位置最大值之和(如果没有的话要取 \(0\))。因为偶数位置总是正数,奇数位置总是负数,并且偶数包含第 \(0\) 个位置所以有 \(0\),奇数总是第一个数,所以这实际上就是全局前缀和的 \(\max-\min\)。
QOJ3014. Cut it Out!
想到了区间 dp,但是问题在于这个东西显然完全没办法合并,于是就扔了。
事实上我们考虑倒着做。注意到如果你现在手上有一个区间的凸壳那么你切掉中间一个位置相当于得到完全子问题的两半。并且因为凸性,这个区间凸壳的边界一定就是最边上两条直线加上外层多边形围起来的。amazing 啊!
于是考虑维护 \(f_{l,r}\) 表示我现在考虑 \(l\to r\) (顺时针方向)这个凸壳,边界是 \(l,r\) 围出来的(换句话说 \(l,r\) 已经被切掉了)。考虑枚举 \((l,r)\) 中的下一个切割点,之后的部分是递归的,我们只需考虑怎么计算贡献。
考虑这条直线的交点可能是外层多边形上也可能是两条直线上,我们可以把这四个点都给搞到。因为四个点肯定在同一条直线上,所以按照 \(x,y\) 随便选个关键字顺序排一下序,那么贡献的两个点就是内部多边形这条边线段两个端点往外的两个点。写一下点之间的偏序关系就行了。
P11262 [COTS 2018] 题日 Zapatak
逆天哈希题。
一个简单的做法是在两个区间的权值主席树上进行二分,但这太丑了。
考虑我们怎么找出两个区间里那两个不一样的元素 \(x,y\)。
我们可以尝试维护方程,抵消掉相同的项。一个简单的办法是维护 \(\sum a\) 和 \(\sum a^2\),这样我们可以简单地获得 \(x-y\) 和 \(x^2-y^2\),然后使用平方差公式把 \(x,y\) 解出来。\(x-y=0\) 的情况显然要么是完全一致要么是有两个元素不同,可以直接判掉。
解出来之后我们只需把它们挖掉然后查询是否相等就行了。桶哈希即可。
太妙了。遇到这种 \(\mathcal O(1)\) 个特殊元素的题一定要尝试把特殊元素求出来。
P11779 [COTS 2012] 宿舍移动 / BUKA
为啥我一道交互题都不会?
我会一个 \(\sum siz_i\) 的方法,只能获得 \(80\) 分。操作指南就是先找出子树的根,然后往两个儿子分配,做子问题。显然在找出根之后只需要把子树内的点连成一棵树,对树染色即可(可以通过 LCA 是否是子树的根判定在同个子树或不同子树)。考虑我们随机一个点开始往所有点连边(也就是把子树内的点连成菊花),这样需要 \(siz_i-1\) 次操作,并且这些操作中查出来的 LCA 的绝对众数应该就是根。特殊情况是随到的点就是根,此时我们可以重来一次,期望 \(siz_i\) 的概率随到根,多出 \(siz_i-1\) 的贡献,匀下来就是每个点都贡献 \(siz_i\)。
正解和这个几乎完全不是一个思路,so sad。
写出计算操作次数的暴力可以发现,如果我们可以砍掉一半的 \(siz_i\) 就能过了。我们就没有什么办法可以只做一边子树吗?
考虑找出当前子树根到底的一条链。因为我们不在乎左右儿子关系,直接钦定它是最左链,然后如果我们可以求出所有点到这条链链底的 LCA 就能分配点集了。
考虑怎么求出这条链,以及怎么分配点集。考虑我们先随一个点 \(x\),然后再随便问一个没有问过且不等于 \(x\) 的点 \(y\)。此时会出现三种情况:
- \(\operatorname{LCA}(x,y)\) 是一个未知的点。这说明 \(\operatorname{LCA}(x,y)\) 是 \(x\) 的一个祖先,并且之前从未出现过,我们把这个祖先添加到最左链中。
- \(\operatorname{LCA}(x,y)\) 是一个已知的点,但不是 \(x\)。这种情况没什么影响。
- \(\operatorname{LCA}(x,y)\) 是 \(x\)。这说明 \(y\) 比 \(x\) 更深,可以放在最左链上。为了便于我们分配 \(y\to x\) 路径上那些点右子树内的点(需要确定这些点和链底的 \(\operatorname{LCA}\)。不过没必要是链底,\(y\) 就行了),我们把 \(x\gets y\),然后递归继续做。
这样显然是对的。注意到我们还需要还原最左链,在过程中维护一下每个点右半子树大小就好了,显然从大到小对应了从上到下。
询问次数的式子是 \(f_n\gets n-1+\sum\limits_{i=1}^{\log_2n}\frac{n}{2^i}\),打出来一看刚好 \(4.9\times 10^4\)。
CF1140F Extending Set of Points
卡在了二分图的合并贡献,临门一脚。太邪恶了。下面是我在白板上的完整思路。
显然考虑线段树分治,于是只用加边了。
考虑 \((a,b)\) 显然刻画成 \(a\to b\),然后考虑怎样我们会连边:
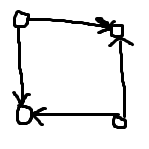
可以发现,在这个四元环上任少一条边都会把那一条边补齐。
不妨观察在一个环结构上进一步添加一些边产生的变化:
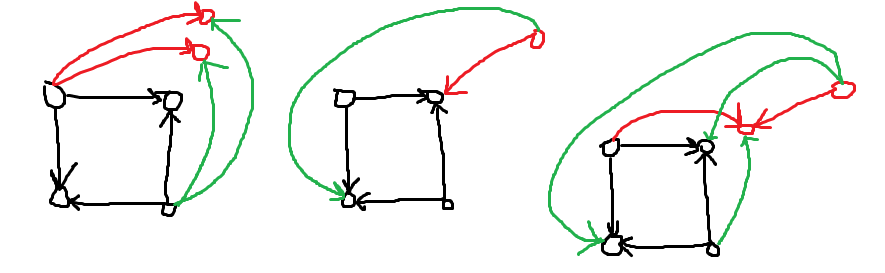
可以发现最后一种图要么入度全是 \(0\) 要么出度全是 \(0\)。我们尝试整理一下最后一种图:
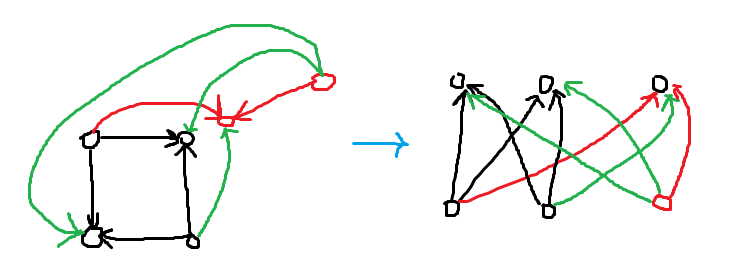
amazing 啊!整个东西构成一个完全二分图。进一步地我们容易发现这个是可以推广的。只要我们连起来一条边,就是把两坨二分图合在一起,并且构成完全二分图。容易发现这是正确的:
假设黑点构成一个完全二分图,红点构成一个完全二分图(省略了部分边)。假设我们添加绿边,那么可以发现:
- 会产生紫边这样的边,它以一个“绿红红紫”颜色的环被加入。
- 会产生蓝边这样的边,它以一个“绿黑蓝红”颜色的环被加入。
- 这个二分图中其他的同部点也会受到影响,会添加左侧橙边这样的边,它以一个“绿黑黑橙”颜色的环被加入。进一步地它将通过一个“橙红红橙”颜色的环生成右侧的所有橙边,把一个黑点和所有对部的红点连起来。
于是整个东西还是连成一个完全二分图了。
考虑我们的连边并不总是像绿边这样理想地对部连。可能会在两个二分图的同部之间连接。可以发现其实同部和对部都是相对的,一个点作为它所有入边的上部点,同时也作为它所有出边的下部点。当我们连接一条边的时候,只是把对应的两层点构成的完全二分图合并在一起了,与其他部分无关(比如说上部点往下一层连的边并不会产生影响,以及上一层往下部点连的边也不会产生影响)。
所以考虑拆点,我们把一个点拆成入点和出点,也就是把层拆开。每次连边直接用 dsu 维护所在的完全二分图及其上下部点数量。显然完全二分图的边数就是上下部点的乘积,合并完之后重算贡献即可。
撤销是简单的。
int q;
map <pii,int> lst;
map <pii,int> memo;
int f[N];
int sz[N],szu[N],szd[N];
ll ans;
int find(int x){
if(f[x]==x) return x;
return find(f[x]);
}
stack <pair<int&,int>> his_f,his_u,his_d,his_sz;
void merge(int u,int v){
u=find(u),v=find(v);
if(u==v) return;
if(sz[u]>sz[v]) swap(u,v);
ans-=1ll*szu[u]*szd[u];
ans-=1ll*szu[v]*szd[v];
his_u.push({szu[v],szu[v]});
szu[v]+=szu[u];
his_d.push({szd[v],szd[v]});
szd[v]+=szd[u];
ans+=1ll*szu[v]*szd[v];
his_sz.push({sz[v],sz[v]});
sz[v]+=sz[u];
his_f.push({f[u],f[u]});
f[u]=v;
}
void rollback(int gl){
while(his_f.size()!=gl){
his_u.top().fi=his_u.top().se;
his_u.pop();
his_d.top().fi=his_d.top().se;
his_d.pop();
his_sz.top().fi=his_sz.top().se;
his_sz.pop();
his_f.top().fi=his_f.top().se;
his_f.pop();
}
}
vector <pii> ofl[N<<2];
#define mid (l+r>>1)
void modify(int p,int l,int r,int ml,int mr,pii x){
if(ml<=l&&r<=mr) return ofl[p].pb(x),void();
if(ml<=mid) modify(p<<1,l,mid,ml,mr,x);
if(mid<mr) modify(p<<1|1,mid+1,r,ml,mr,x);
}
void calc(int p,int l,int r){
int tmp=his_f.size();
ll tans=ans;
for(auto x:ofl[p]) merge(x.fi,x.se);
ll bans=ans;
if(l==r){
cout<<ans<<' ';
rollback(tmp);
ans=tans;
return;
}
calc(p<<1,l,mid);
ans=bans;
calc(p<<1|1,mid+1,r);
ans=tans;
rollback(tmp);
}
#undef mid
int main(){
#ifdef Shun
freopen(".in","r",stdin);
freopen(".out","w",stdout);
#endif
ios::sync_with_stdio(false);
cin>>q;
fr1(i,1,600000) f[i]=i,sz[i]=1;
fr1(i,1,300000) szd[i]=1,szu[i+300000]=1;
fr1(i,1,q){
int x,y;
cin>>x>>y;
if(lst[mp(x,y)]){
modify(1,1,q,lst[mp(x,y)],i-1,mp(x,y+300000));
lst[mp(x,y)]=0;
}
else lst[mp(x,y)]=i;
}
for(auto i:lst){
if(i.se!=0) modify(1,1,q,i.se,q,mp(i.fi.fi,i.fi.se+300000));
}
calc(1,1,q);
ET;
}
//ALL FOR Zhang Junhao.
这太有趣了。
P9168 [省选联考 2023] 人员调度
\(\mathcal O(nm\log)\) 的做法是简单的。考虑我们每个点上只留最大值,等价于把小的人都删了,于是显然我们存在一个自底向上用可并堆贪心的做法:每次只需要把所有儿子里的人合并进来,然后注意到这个子树根上的人可以任意下放到最多填满,所以把最小的几个弹掉就好了。这个东西可以获得 \(48\) 分。
这样会有一些点的子树是“满的”。
然后考虑怎么做正常的题。我们可以线段树分治,这样只需研究加点。考虑加一个点影响它到根的一条链,如果这条链上没有任何满的子树,那么这个人可以直接上去,显然没有问题。
但是如果路上有满的子树,那么这个人可能要置换此处向上的堆中一个人的位置。
一个简单的想法是,假设我们能够维护每个点 \(x\) 上并出来表示到这个点子树内还在的所有人,记作集合 \(s_x\)。那么我每次向上找到第一个满的子树,然后尝试弹出最小的那个人。这样做的坏处是,我把这个点置换之后我需要继续维护祖先的 \(s\) 集合,因为这个人不但不一定能到根,而且因此还可能会影响之后的弹出,这很坏了。
这显然是换的人的问题,我们应当尝试使得每次有效的换人性质更加漂亮。可以发现只有换掉能到达根的人才有意义(换下了到不了根的人自己也一定会被弹出去,因为被保留的人都比自己大),那么我们不妨构造刚刚那个集合的缩减集,把这种人排出去:假设能够维护 \(s_x\) 表示 \(x\) 子树内能到达根的人的集合。这样当我们向上遇到第一个满的位置的时候,尝试把 \(s_x\) 的最小值扔掉,容易证明满的子树总是可以完成这个调整。由于这并未影响这个位置向上的集合大小,并且由于这个人一定更大,所以这个人不会影响上面的弹出(上面需要弹掉的值一定比删掉的小),且不可能反倒无法到达根。
由于只有加点,扔掉的东西不会再回来。
性质太美好!怎么维护呢?
显然可以树剖解决。我们维护每个点子树内部有多少人,当人数达到 \(siz\) 的时候这个地方就满了;\(s_x\) 也无需真实地维护在每个点上用合并的方式计算,因为这里“能到达根”相比“能合并到这里”是全局信息和部分信息的差别,这里我们可以尝试直接全局地维护能到达根的人,把信息下放到人上转置问题。这样每个点的 \(s_x\) 就可以看成就是子树里面“有颜色”的人们,我们直接到每个点上维护该点上能到达根的人,需要时查询子树信息即可。
考虑我们加人的时候找到第一个满的位置只需在线段树上维护区间减(以 \(0\) 作为报警器)并支持查询最小值和最小值位置即可,而维护“能到达根的那些人”可以发现只有加删人和查询子树 \(\min\)。
实现细节上,每个点上要挂一个 multiset 维护能到达根的那些人,因为每个树上的节点可以贡献一堆人,又要作用删人。想清楚了才好写。
这样做复杂度是 \(\mathcal O(n\log^3 n)\) 的,因为树剖 2log,还有线段树分治。不过常数很小能过。
恰当地选择维护的信息真的好厉害。
P11980 [KTSC 2021] 会议室 / meeting
为啥不会这种题。思维定势太严重了吧。
考虑删掉最小不好做,反过来考虑添加最大。然后显然应该 dp。
然后不要考虑按照什么方法给区间排序,这会陷入泥潭之中。我们抛弃在区间序列上 dp,而直接在格子上 dp:考虑 \(f_i\) 表示目前最后一个连通块最右侧是 \(i\) 的最大权值。转移的时候,我们从 \(j<i\) 转移过来,用 \(f_j\) 加上完全在 \((j,i]\) 中的区间的前 \(k\) 大权值转移即可。显然里面是不是一个连通块不影响,我们总能转移到最优秀的方案。
考虑如何快速计算 \((j,i]\) 中区间的前 \(k\) 大权值。考虑扫描 \(r\),然后向前扫描 \(l\),我们可以简单地用一个大根堆维护前 \(K\) 大。然后就做完了。
ZR21 省选第三轮集训 Day 1A 游戏
记一种 \(\alpha-\beta\) 博弈论套路。
通常来说维护自己减对面的策略是复杂的。所以我们考虑先把所有权值全部判给一个人,这样就干掉了一个人操作产生的影响,这样我们只需要考虑另一个人的策略就行了。这个套路同样用于解决 P4363 [九省联考 2018] 一双木棋 chess 和一个 ABC 的对抗搜索题,不过好像不用也行。
那么这个题我们肯定先把所有题染红,把权值给成 \(\sum w\)。然后考虑一条边如果一黑一红就产生 \(-w\) 的贡献,两黑就产生 \(-2w\) 的贡献,所以我们把贡献丢到点上,选择一个点就是产生了它周围所有边的边权和的贡献减掉。
所以 B 选择一定是选周围所有边的边权和最大的点,A 也是选择这样的点来阻止 B 选择。所以本质上就是维护一个奇数大的数的和,并支持修改。显然线段树或平衡树都可以使用。
ZR21 省选第三轮集训 Day 1B 最短路
为什么能想到?????
统计全局贡献,考虑分治。注意到这个连边产生的好处是每 \(3\) 个连续位置当中至少有一个是被最短路经过的,所以我们直接把 \([mid-1,mid+1]\) 空出来,在这三个点上计算跨越产生的贡献,然后递归 \([l,mid-2]\) 和 \([mid+2,r]\)。
考虑这三个点开始和结束产生的贡献可以直接一个拓扑排序算完,这是 \(\mathcal O(r-l)\) 的。
然后考虑经过这三个点产生的贡献。一对 \((S,T)\) 产生的贡献是 \(dis(S,mid-1)+dis(mid-1,T)\) 等三者的 \(\min\)。显然我们应该拆成六份统计每份产生贡献的次数。
以 \(dis(S,mid-1)\) 和 \(dis(mid-1,T)\) 为例,它们产生贡献当且仅当 \(dis(S,mid-1)+dis(mid-1,T)\le dis(S,mid)+dis(mid,T)\) 且 \(dis(S,mid-1)+dis(mid-1,T)\le dis(S,mid+1)+dis(mid+1,T)\),由于所有点和 \([mid-1,mid+1]\) 互相到达的距离都是计算好的,所以移项之后就是两个只关于 \(S,T\) 上权值的不等式,直接二维数点即可。
注意计算 \(mid\) 和 \(mid+1\) 时需要斥掉距离相等的走法,所以要修改不等式的取等。
时间复杂度 \(\mathcal O(n\log^2 n)\)。
CF1234F. Yet Another Substring Reverse
为啥不会 *2200????
考虑翻转的意思就是可以随便选两个不交子串合在一起,只要这两个子串合在一起没有相同字符就行。
考虑不合法不优,显然交的子串一定有相同字符。所以我们就等价于随便选两个子串,合在一起没有相同字符则对答案贡献长度和。因为子串长不可能超过字符集大小(否则一定有重复字符),显然我们可以先预处理所有内部没有重复字符的子串,并计算它们中含有的字符集。
剩下的问题相当于在这些子串里面选择两个串使得交集为空,最大化并集。考虑枚举其中一个,相当于在它的补集的子集中找一个最长的,高维前缀 \(\max\) 即可。
P7618 [COCI 2011/2012 #2] FUNKCIJA
我不知道我为啥一直在想每个点上插一个多项式,就是不 dp。
考虑我们等价于找一个 \(\{a_{26}\}\) 序列,满足一堆条件。其中一些条件类似 \(a_j\le a_i\) 之类的。
容易想到对于这种条件连边。显然外层的不会依赖内层的,所以我们从外层变量向内层变量连接,表示外层变量限制内层变量。这样会得到一棵树。
可能可以考虑在树上进行多项式插值,但我们不妨考虑 dp。\(f_{x,i}\) 表示 \(x\) 点上值为 \(i\) 时子树的方案数量,考虑向上的时候受到限制,贡献是一个和式再积,所以可以前缀和优化。复杂度 \(\mathcal O(nV)\)。
CF348C Subset Sums
根号分治,四种贡献想清楚就好了。https://www.luogu.com.cn/article/i3dc5624
CF467E Alex and Complicated Task
考虑 dp。如果我们朴素地 \(f_{i,j,0/1/2/3}\) 表示子序列以 \(i\) 结尾,这个数作为模 \(4\) 后的 \(0/1/2/3\) 位置,上一个数是 \(j\) 的最长长度,那么转移将非常复杂,根本无法优化。
所以考虑我们直接四个四个转移。\(f_i\) 表示子序列以 \(i\) 结尾的最长长度。考虑前面找三个点 \(p<j<q\),使得 \(a_p=a_q,a_j=a_i\),然后我们转移 \(f_i\gets \max\limits_{k<p} \{f_k\}+4\)。
考虑我们肯定希望 \(p\) 越大越好,所以我们只需对每个 \(i\) 求一个最大的 \(p\) 满足存在合法的三元组 \((p,j,q)\) 即可。
考虑使用数据结构方法会很困难,考虑有没有无用状态。注意到这样一件事:如果 \(q<pre_{i}\) 那么我不妨在 \(pre_i\) 转移这个三元组,肯定比这里优秀。所以我们只需考虑 \(pre_i<q\) 的部分。那么 \(j\) 肯定就是 \(pre_i\) 了。
于是我们只需对每个 \(i\) 查询一个最大的 \(p\) 使得 \(pre_i<nex_p<i\land p<pre_i\),这就是一个二维数点。我们离线线段树即可。
剩下的就是直接 dp,垒一个前缀 \(\max\) 即可。
upd:想完发现这题我写过做题记录,也过了…… https://www.cnblogs.com/lemonniforever/p/18571330#cf467e-alex-and-complicated-task
P3147 [USACO16OPEN] 262144 P
没认真想。
一个简单的想法是区间 dp,然后我们发现我们根本不用区间 dp,因为每个左端点 \(i\) 凑出某个数 \(j\) 的区间显然肯定是唯一的。
所以设 \(f_{i,j}\) 表示从 \(i\) 开始凑出 \(j\) 的唯一右端点。转移是简单的。
考虑 \(j\) 的大小:可以发现我们想生成一个 \(+x\) 的数至少需要吞并 \(2^x\) 个原元素。所以最多只有 \(58\)。
于是做完了。
P12306 [ICPC 2022 WF] Doing the Container Shuffle
考虑我们把每一段分开计算:我们求出 \(a_i\) 上车之后,\(a_{i+1}\) 到达栈顶期望要移动多少个集装箱,换句话说,\(a_i\) 和 \(a_{i+1}\) 中间期望有多少个必须移动的集装箱。考虑怎样的一些集装箱有移动的必要:
- \(a_j\),且 \(j\) 满足 \(i+1<j\le n\),因为 \(<i+1\) 的集装箱都上车了,\(=i+1\) 的到达栈顶不需要再移动。
- \(a_j>\min(a_i,a_{i+1})\),否则这些集装箱不可能在它们上面。
实际上,我们可以证明每个满足条件的集装箱都有 \(\frac{1}{2}\) 的概率需要被移动。不妨假设 \(a_i<a_{i+1}\) 且 \(a_i\) 装在栈 \(1\) 里,那么分类讨论:
- \(a_j<a_{i+1}\) 时,这个集装箱有 \(\frac{1}{2}\) 的概率装在栈 \(1\) 里,\(\frac{1}{2}\) 的概率装在栈 \(2\) 里。显然,如果这个集装箱装在栈 \(1\) 里,那么它就一定出现在 \(a_{i}\) 和 \(a_{i+1}\) 中间,需要移动,否则不需要。
- \(a_j>a_{i+1}\) 时,如果 \(a_{i+1}\) 装在栈 \(2\) 里,那么它就一定出现在 \(a_{i}\) 和 \(a_{i+1}\) 中间,需要移动,否则不需要。
两者概率合起来就是 \(\frac{1}{2}\)。
于是简单二维数点即可。
P12298 [ICPC 2022/2023 WF] Carl’s Vacation
不会。 【模板】三分套三分。感觉至上的一道题。
显然,如果我们确定了从其中一个金字塔离开的点位,那么另一个应该是单峰的。
进一步地考虑,每个点上的最优解应该也是单峰的。所以直接三分套三分。
P12307 [ICPC 2022 WF] Zoo Management
不会。这玩意是紫题?看了半个小时群论也搞不明白,感觉讲群论没一个能讲明白的。。
显然唯一的操作是对着一个环做循环移位。
先考虑做一遍边双,这样拆成子问题,我们只需对每个边双检查可行性就行了。
考虑边双的形态:
- 一个环,那么可以简单地字符串匹配。
- 一个边仙人掌。
- 不是一个边仙人掌。
我们先考虑不是一个边仙人掌,换句话说存在一条边同时在两个简单环里面,这实际上等价于我们总可以在它的某个点对之间找到 \(3\) 条边不相交点不相交路径。(我觉得可以证明是点不相交,但是 WF 题解写着边不相交)
Proof.
考虑如果这两个简单环有交,那么某个环上不交的一个部分将构成一个合法的点对:
由此,只要不是一个边仙人掌,那么存在一对点上产生三个简单环。
然后开始架群论。考虑我们整个东西显然是一个对称群 \(S_n\) 的子群(边双一定是一堆环的并),操作就是一个 cycle。Jordan's theorem 告诉我们只要产生一个质数大小的 cycle 就说明这个子群要么是它的交错群要么是这个对称群本身。换句话说,我们要么可以做到任何排列,要么起码可以做到它的偶排列。
我们可以证明,这两种图都一定存在一个 \(p\)-cycle。先证明边仙人掌:
考虑一个点上存在两个 cycle \(a,b\),那么我们可以通过 \(aba^{-1}b^{-1}\) 的方式构建一个 3-cycle,就像这样:
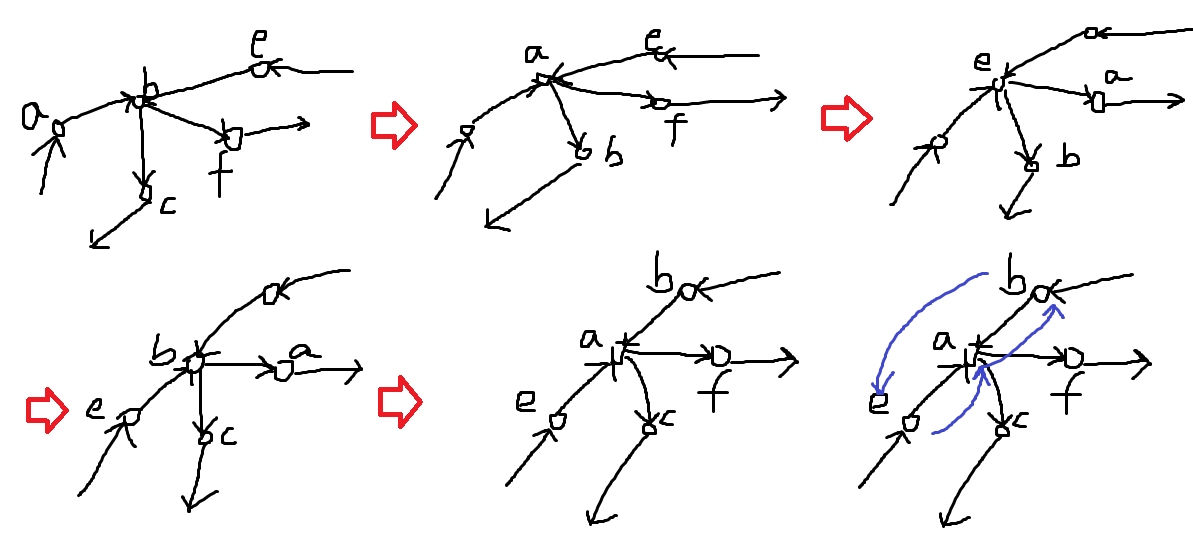
然后可以证明非边仙人掌存在一个 2-cycle:
[TBC]
CF753C Interactive Bulls and Cows (Hard)
不知道为啥特别想做一下这种奇怪的题。
显然这是一个类似 wordle 的东西,我们考虑直接用信息熵。THUSC2024 Day2 的学习资料告诉我们,某状态下一个猜测产生的信息熵形如
其中 \(S\) 表示某种返回值情况下剩余的答案集,\(p_S\) 表示它占据原答案集的大小,即条件概率。我们对所有可能求和即可算出信息熵。
我们直接在每个状态下都选择信息熵最大的情况就行了。
P8079 [WC2022] 猜词
和上面一样,我们每次扫一遍词库爆算信息熵。容易发现枚举返回值不太合理,复杂度太高了,所以改成枚举返回的串去推返回值,然后加入对应的决策,以此计算信息熵时间复杂度就对了。
直接写可以获得 \(91\) 分,优化首词(词库里面出现次数最多的字母是 \(\texttt{r,l,t,s}\),所以我们可以简单地用 tirls 作为首词,也可以打表所有首字母下最大信息熵的第一次猜测)之后可以获得 \(96\) 到 \(97\) 分。
然后考虑我们如果按照信息熵一个一个来基本上不太可能 \(3\) 次就能搞定,但是如果最后只剩很少的词了可以直接撞一个,对了就对了,没对大概率也能筛掉一车子,所以我们对信息熵的估价进行偏移,如果词在候选答案里面就增加 \(\Delta\) 的贡献,取 \(\Delta=0.1\) 可以在本地获得 \(99.55\) 分,交上去四舍五入就过了。
[沙东省集] 最小生成树(mst)
我真的不会做这种稀里糊涂复杂度的题。
让我们对其使用最小生成树算法,在状态里面维护就好了。考虑 Kruskal 或者 Boruvka 开始都可以得到相似的结果:我们一条边一条边往里面加,合并连通块。从 Kruskal 的角度来说会更直接一些,我们从小到大枚举边,在所有可合并的状态中合并连通块并计入贡献。可以注意到所有本质不同的连通块划分方案是 \(\text{Bell}(n)\),\(n=9\) 时仅有 \(2\times 10^4\)。
进一步的问题是我们如何解决一条边只能在两种决策中选择一种的问题。考虑我们可以拆边,拆成一条小边权一条大边权,把优先权放在小边权上,小边权上随意来,将是否必选是否必不可选的问题丢到大边权上,此时我们发现好处是当我们到达大边权的时候一定要么被最小生成树的性质干掉了这条边都无所谓,要么就两点不连通必须选择,我们就减少了维护的信息数量,不用维护一条边有没有被选过了。
对连通块写一下压位,转移的时候产生一点 \(\mathcal O(\text{Poly}(n))\) 的复杂度应该也没事,\(\mathcal O(m^2\text{Bell}(n))\) 可以解决。
[沙东省集] 行走(walk)
考虑走一轮会发生的事情:考虑我现在在点 \(x\),那么我会先递归到若干个儿子子树,然后由于 \(c(x)_{cur_x}\) 是父亲而走回去。此时这个点上的 \(cur_x\) 就指向父亲了。
进一步地我们发现,当 \(cur_x\) 指向父亲之后,之后每次一定是扫描一遍完整的儿子,然后回到 \(cur_x\) 是父亲的状态走回父亲,相当于 dfs。
因此在 \(\mathcal O(n^2)\) 次行走之后一定所有 \(cur\) 都指向父亲(在还存在点的 \(cur\) 没有指向父亲的情况下,我们一定可以每走一次把一个掰对,考虑最浅层的那个就),之后就是正常 dfs 过程了,顺序就是欧拉序。
因此,我们只需考虑前 \(\mathcal O(n^2)\) 次怎么整。
我们每走一次就能把一个掰对,考虑复杂度瓶颈实际上在于我们每次都要重新扫一遍树,如果我们能步步紧逼,每次都能掰对一个点的话那其实暴力也是对的。
考虑每次从 \(1\) 开始走的过程:我们最初应该是正常沿着欧拉序移动,只要一路上都是指向父亲的点就没什么问题,直到走到一个 \(cur\) 不是指向父亲的点。我们只要快速跳过这个过程,在遇到没掰对的点的时候显然它下面的点肯定没一个是对的,所以对它实施暴力向下做就行了。
快速跳过可以使用并查集或者链表。
为啥这么简单。
P10768 「CROI · R2」落月摇情
太卡常了。
考虑一个一般的思路:我们直接上 trick from merging 进行多路归并。那么有两件事需要注意:第一我们应该快速跳过已经连通在一起的部分的边,因为我们需要使得整个图连通;第二我们应该优先把所有负数连上。
考虑我们不太方便一边控制连通性一边控制负数,所以我们可以先搞定连通性,最后再来一遍多路归并把负数连上。然后你发现我们控制连通性的过程虽然名义上叫多路归并,实则就是 Boruvka:我们对每个点向外寻找权值最小的连上。所以我们实际上实现地证明了一定会先取一个最小生成树保证连通性。
证明也是简单的。考虑如果最终我们不包含一个最小生成树作为子图,那么我们必然可以取这个图的最小生成树出来换成最小生成树,一定可以更小。
实际上也不需要写 Boruvka,分类讨论一下就行了。
然后写出来就是非常卡常,卡一下存边方式掉一只 map \(\log\) 就能通过了。
P3441 [POI 2006] MET-Subway
上界代替思考,题解代替大脑。
考虑一个简单的贪心:我们每次选择可以覆盖尽可能多还没有覆盖过的点的一条路径,就这样选择 \(l\) 条。感觉一下显然很正确。
为了简单地强行维护这个过程疑似需要一些比较抽象的结论,此处按下不表。
考虑换一个思路,我们容易发现我们一定是选择 \(2L\) 个叶子拉出来匹配。那么不妨声称:如果我们有不多于 \(2L\) 个叶子,那么一定可以覆盖所有点。
Proof.
考虑存在一个点没有覆盖,我们给它删掉。因为它不可能是叶子,所以一定产生至少两个连通块。显然这些连通块都必然存在至少一条内部路径(因为至少存在一个叶子)。我们任取两个连通块联合起来调整一下它们的路径就能使得路径数量不变且仍然覆盖相同量的点。
然后我们考虑如果有多于 \(2L\) 个叶子怎么办。我们先选择 \(2L\) 个不同叶子,此时我们可以在最外层覆盖 \(2L\) 个点,然后我们考虑把这些叶子删掉之后往里一层,也即现在的叶子。考虑此时我们仍然可以任取一个 \(2L\) 的子集,因为它一定可以往外层对应一个 \(2L\) 大小的子集(考虑这一层的每个点都至少往下一层有一个点连接),可以看作是路径的一部分。如果取不到也没关系,我们允许路径相交,一个点上可以出现多条路径的当前端点挤在一起,所以这一层的所有点都可以覆盖掉,且下一层不影响。
从另一个角度看如果出现了这一层取不到上界的情况,则一定剩下的整棵树都可以被覆盖完。因为随着层数往里,点一定是越来越少的;同时我们也可以看成是覆盖了该树的所有叶子,刚刚已经证明这样一定可以取到整棵树。
于是我们直接从叶子开始向内拓扑排序,对树按照进入拓扑队列的轮次分层,然后每一层取上界即可。
P10855 【MX-X2-T4】「Cfz Round 4」Gcd with Xor
观察异或转化太困难!莫反简单。
考虑先解决一下异或的问题,然后再应用莫反:
其中 \(m\) 是两个 \(\le n\) 的数能异或出的最大值即 \(2^{\left\lfloor\log_2 n\right\rfloor+1}-1\),因为我们转而枚举了 \(j\) 和 \(i\oplus j\)。
显然可以运用差分,于是我们只需对每个 \(j\) 求两次:
考虑固定 \(j\),那么可行的 \(p\) 一定只构成 \(\log m\) 个区间!证明只需考虑逐位确定即可。据此疑似可以导出不需要莫反的 01-Trie 做法,但我觉得太神秘了。
那么现在我们只需考虑可行的区间,并取缔艾佛森括号:
再差分一次:
这个式子只有两个和式且看着就很不神秘,考虑直接使用莫反:
其中代换 \(T\gets dt\) 是我觉得比较难想到的步骤。
现在我们考虑最后一个和式,显然筛出 \(\mu\) 之后枚举 \(d\) 向其倍数垒即可做到 \(\mathcal O(n\ln n)\) 预处理。
然后考虑现在的式子形如 \(\sum\limits_{j=1}^n\sum\limits_{T|j}(\left\lfloor\frac{r}{T}\right\rfloor+1) w(T)\),我们需要对每个 \(j\) 做 \(2\log\) 次后面的和式计算,考虑直接枚举 \(T\) 的因数,复杂度 \(\mathcal O(n\ln n\log n)\),可以通过。
CF704E Iron Man
垃圾数据结构。
考虑树剖,那么每条路径产生 \(\log n\) 条 DFS 序上连续的路径,还有 \(\log n\) 次穿越轻边。考虑我们可以把两部分分开做,因为轻边和重链是全局的,两个盔甲一定相遇在同时是轻边或重链的时候。
考虑同时是重链,我们产生了 \(\mathcal O(n\log n)\) 条在 DFS 序上连续的路径。考虑这些路径在时间上也是连续的,所以我们只需刻画成 DFS 序和时间的平面直角坐标系,找一个时间最小的交点即可。
考虑同时是轻边,虽然轻边两侧点的 DFS 序不连续,但是我们现在只考虑这条边的事所以可以看成是连续的,这条边上的路径就能看成是横坐标为 \(0\to 1\) 或 \(1\to 0\),纵坐标为通行时间的一些线段,我们也只需找一个时间最小的交点即可。
怎么找这个最小的交点呢?
考虑扫描线。我们尝试扫描时间轴,维护一个 set 表示当前时间存在的盔甲的位置按照 DFS 序排序的结果。考虑一个点作为最早的交点拥有何种性质。
容易发现,相交意味着盔甲在 set 中交换了顺序。因此在最早的交点之前所有的盔甲都一定没有变化过顺序,保持着加入时起点的顺序。进一步地,最早的交点一定是两条相邻的线段交换了顺序。
我们考虑直接在扫描时间轴的同时维护线段起点的顺序,我们总是钦定此时仍然没有出现最早的交点(当然如果现在时间大于 \(ans\) 肯定就退出了)。当出现加入线段或者删除线段时,我们只需检查被操作的线段与相邻线段的贡献即可。
于是就做完了。同样的道理可以用来解决典题 P5428 [USACO19OPEN] Cow Steeplechase II S,或者写一个 P9397「DBOI」Round 1 DTTM 的 SPJ。
P10856 【MX-X2-T5】「Cfz Round 4」Xor-Forces
你这交换儿子怎么有诈啊???
考虑一个一般的技巧,我们将异或刻画为整层节点的交换儿子,在区间询问时完成 pushdown。问题是这样我们完全没有办法维护半群信息,因为我们必须要在询问的时候同时完成 pushup,但是下层信息是烂的。
真的烂吗?
考虑我们其实是希望知道一个点 \(\oplus x\) 产生的信息(显然这个 \(x\) 容易维护,类似标记永久化即可),但是实际上线段树任何一个节点上只有 \(len\) 种本质不同的 \(x\),原因显然。考虑我们的信息 \(\mathcal O(1)\),而 \(\sum len=n\log n\),所以我们可以强行维护出每个节点上 \(\oplus\) 一个数得到的信息。
然后就做完了。显然预处理信息是可以线性的。
CF1515H Phoenix and Bits
*3500。这玩意怎么可能会做????为什么题解区都觉得这个题简单???
考虑搞一棵权值线段树,然后我们只需对所有 \(\log\) 个分裂出的区间进行操作。
考虑 \(\oplus\) 典爆了,相当于一堆交换儿子,我们直接打标记,往下删最高位 pushdown 即可。
考虑 \(\&\) 和 \(|\) 就很困难了。然后我们发挥【位运算高手】的技能可以发现,两个数的 \(\&\) 其实就是它们补集的 \(|\) 的补集。我们可以用 \(\oplus 2^{20}-1\) 来获得补集,于是 \(\&\) 被 \(|\) 和 \(\oplus\) 平替。
考虑 \(|\) 怎么办。可以发现 \(|\) 大概形如要把左儿子合并到右儿子,这个操作不方便维护信息,于是我们想到线段树合并。考虑类似线段树合并的复杂度,我们只要合并节点就变少,所以尝试直接对其 \(1\) 位表示的层的点找出来,然后暴力合并,合并完之后继续向合并出来的树找点,直到不能合并即可。找点的均摊是简单的:考虑每次有效的合并至少减少一个点,所以至多找 \(\mathcal O(n\log V)\) 次点,我们可以简单地做到 \(\mathcal O(\log V)\) 的找点。只需要直接扫整棵树,同时确保每次向下 DFS 的时候总有一个有效合并的点(即左右儿子都存在的点)在等着我们就行,显然可以压位地维护此信息。无效的合并(即两个儿子有一个是空的,不涉及树合并)只需要打标记就可以了。
这个合并的复杂度显然等价于线段树合并。考虑我们每次扫描了至多 \(3\) 倍共同拥有的点的数量次(自身加上这种点的“叶子”的两个儿子),而这将导致总点数减少共同拥有的点数,所以总扫描点数就是 \(\mathcal O(n\log V)\) 的。
最后我们只需要考虑所谓的 \(|\) 标记和 \(\oplus\) 标记的合并就行。考虑前者是把左儿子干成右儿子,后者是交换儿子,我们显然需要引入右儿子干成左儿子这种标记(实际上也算是所谓的 \(\&\) 标记了),然后容易发现这三种标记封闭,就容易维护了。
于是就做完了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号