Hey Gift:我听着冬夜的安宁 亿万分之一的一颗
标题:TOP 登陆少年-张泽禹《Talk to the Star》(Remake Ver.)
如果在 NOIP 后没有退役,本做题记录应该就会作为这个冬天的做题记录了。
QOJ6107. One Path
思路还是比较直接的。
手玩样例可以感觉出来,每次虽然允许我们连成一个图,但我们连成一棵树会更好。证明容易通过刻画答案形态证明。
那么就可以转化成,我们需要从这棵树上切掉 \(k\) 条边,让这 \(k\) 条边的边权和加上切分出来的子图的直径和最大。
如果答案可以继承那么题是好做的,直接粘一个鼓 C 过来改改就可以了。然而答案是不可以继承的,可以被下面这个东西 Hack 掉。

那么显然只能树形 dp。
\(f_{u,i,0/1/2}\) 表示在 \(u\) 子树内砍了 \(i\) 次,很明显只会有三种形态:
- 子树内有 \(i\) 条路径已经选出,其中 \(i-1\) 条已经完备,但是最后一条路径还没有找到哪条边被砍掉来划分出。
- 子树内有 \(i\) 条路径已经选出,其中 \(i-1\) 条已经完备,但是最后一条路径还没有找到哪条边被砍掉来划分出,并且是一条链。
- 子树内有 \(i\) 条路径已经输出,其中 \(i\) 条都完备。
最后对于砍 \(i\) 次的答案我们只需输出 \(f_{rt,i+1,0},f_{rt,i,2}\) 的最大值即可,因为根节点所在连通块自然是一个划分,砍 \(i\) 次应该产生 \(i+1\) 条路径。注意我们应该只对 \(k\in[0,n-1]\) 进行 dp,后面的都等于 \(n-1\) 处的答案。
树形背包转移即可,时间复杂度 \(\mathcal O(nk)\)。
QOJ8840. Lalo's Lawyer Lost
首先树上做这个是 well-known 的。
我们考虑树上那个结论是怎么来的:考虑答案上界,对于任意一条边 \((u,v)\),考虑拆掉这条边后的两个子树大小 \(sz_u,sz_v\),那么这条边最多向匹配贡献 \(\min(sz_u,sz_v)\),这表示从其中较小的那个子树延伸出匹配产生的贡献。然后可以证明上界是可达的,只需要随便选一个点当根,每次选择不同子树内的一对点即可,画一下图可以容易理解这个构造。
然后考虑仙人掌怎么办。不在环上的边类似操作,在环上的边需要特殊考虑。首先我们可以先用仙人掌性质把整个树缩成这个环,然后考虑这个环的贡献。
此时我们采用树上那个结论的另一个证明:所有匹配的路径必然是相交的。可以发现任意两对不相交的路径换成相交总是可以更好的。

显然这应用到这个环上也是正确的。

所以我们直接把环上所有相对的点(显然需要带权,换句话说需要把一个点展开成它管理的子树大小个点)匹配就好了。
CF1363F. Rotating Substrings
很难的 dp 啊。我真的不会做。/ll
考虑我们 Rotate 一个子串本质上是提取一个字符到前面去,考虑刻画这个会更方便一些。可以发现一个字符至多操作一次,所以我们可以考虑固定一些不操作字符,这样反过来做的好处是这种不操作字符只会向后走。答案就是 \(n\) 减去这些字符的最多数量。
可以发现这些字符就是 \(s,t\) 的一个 LCS,但是需要 \(t\) 中总在 \(s\) 后方匹配,因为固定的字符只会向后走。
然而你发现这是错的。考虑下面这个东西:
caaebbb
abbceba
我们不能固定 c e b,因为 e 前面有两个 a,但是 \(t\) 中 e 前面只有一个 a。我们不可能在不操作 e 的情况下让 e 前面的 a 数量减少,因为字符不能跳跃地往后走,只能整个后缀往后。所以我们对 LCS 再增加一条限制,要固定字符对 \((s_i,t_j)\),必须对于所有字母,在 \(s\) 中 \(i\) 前面的出现次数始终不超过 \(t\) 中 \(j\) 前面的出现次数。
这样直接 dp 就是对的。
还有一点小问题。显然这个条件还需对 \(t_{n+1}\) 满足,因为对于最后一处固定后的部分也同样需要限制。但我们发现这是自然的。
CF1015F. Bracket Substring
简单题,显然记录 \(f_{i,j,k}\) 表示长度为 \(i\),匹配到了第 \(j\) 项,净左括号数量为 \(k\) 的方案数。用 KMP 维护第二项并确保第三项不为负数。当 \(j=|S|\) 时不再继续进行转移(即把所有合法字符串钦定到第一次出现 \(S\) 处计数)。最后对于所有 \(f_{i,|S|,k}\) 再乘一个系数就行。
CF467E. Alex and Complicated Task
不可战胜!
首先可以证明一个关键的性质,由这个性质我们可以得到许多做法。
对于任何四元组 \((x_1,y_1,x_2,y_2)\) 满足 \(a_{x_1}=a_{x_2},a_{y_1}=a_{y_2}\),总有 \(pre_{x_2}=x_1\)。
我们可以考虑一个 dp 过程在 \(x_2\) 处寻找上一个已经完备的四元组转移过来。经过讨论很容易证明不选 \(pre_{x_2}\) 时一定存在等价或更优秀的选择一对 \((pre_x,x)\) 的选法。
我们可以立即获得一个基于 ds 的简单 dp,此处不再展开。提一个极度简单的线性贪心做法。
我们考虑这个东西满足贪心:只要存在一个合法四元组就立即加入答案。注意到这个四元组往后面留也最多贡献到一组里面,所以在这里加入一定更好。
这个贪心带来的另一个好处是:存在合法四元组之后我们就能把问题从这里切割开,后面是一个子问题。
于是考虑怎么找出合法四元组。我们考虑枚举 \(x_2\),那么我们只需要把 \(pre_{x_2}\) 到 \(x_2\) 中间的所有颜色都打上标记:这意味着在此之后出现任何标记过的颜色都将直接产生一个四元组。所以我们可以在枚举 \(x_2\) 的同时也判定四元组。
打标记是简单的:打过标记的颜色可以直接丢弃。我们使用一个队列或者栈维护就可以了。
因为值域问题所以维护标记和 \(pre\) 需要使用哈希表。
这样就做完了。太牛逼了。
QOJ1089. Biological Software Utilities
感觉今天精神状态很差……
很简单的题。考虑直接数我们其实不太有办法的,于是考虑邪招。
我们可以构造性地证明:任何一棵存在完美匹配的树的完美匹配都一定是唯一的。
Proof by Qingbai
考虑这棵树的完美匹配的获得方式:不断从叶子开始,叶子取父亲匹配,然后删掉这两个点。这样的构造是唯一的。
于是我们只需要对于所有可能的匹配结果计数它能还原出的有标号无根树数量就可以了。
所有可能的匹配结果数实际上等价于 SA 在 EC-Final 提出的分房间问题。
Problem by StayAlone
有 \(n\) 个人(\(n\) 为偶数),这 \(n\) 个人均匀地分成两队,求住入 \(\frac{n}{2}\) 个双人间后所有房间的人都不是同一队的方案数。房间之间本质相同。Solution by Shunpower
我们考虑所有 \(n\) 个人按照从左到右排开,每两个人一间的分房方式,这样是 \(n!\) 的。考虑到房间本质相同,并且不区分住入的人的顺序,所以实际上一样的分房一定被数了 \(\frac{n}{2}!2^{\frac{n}{2}}\) 次,用 \(n!\) 把它除掉就可以了。
考虑到我们这里最后也就是把 \(n\) 个点分成两半,得到一个不区分顺序也不区分边两端顺序的大小为 \(\frac{n}{2}\) 的边集,所以可能的结果数也是 \(\frac{n!}{\frac{n}{2}!2^{\frac{n}{2}}}\)。
然后我们考虑每种边集能还原出的有标号无根树数量。此时我们可以把一条边看成一个整体,然后做有标号无根树数量(即 \(\frac{n}{2}^{\frac{n}{2}-2}\))。只需要再注意一下边与边之间连接有四种方式都不同就可以了。这样显然可以对应回一种方案,所以是对的。
QOJ671. Shortest Path Queries
首先用线段树,pushup 时传递闭包,可以轻易获得一个 \(\mathcal O(w^3h\log h+qw^3\log h)\) 或者使用 Dij 做到小一点的做法,不过比较难过。
考虑沿用线段树方案。但我们考虑另一个思考方向:类似标记永久化的,如果区间拆开再组合不好做,那么不妨把区间放到覆盖它的区间上直接查询答案。
显然按照 \(h\) 建立线段树。考虑一个询问在线段树上移动。这里为了方便我们记抠掉 \(mid\) 的线段树(即左儿子是 \([l,mid)\),右儿子是 \((mid,r]\))。如果这个询问被完全包含在左节点或右节点中,那么我们递归向下做即可。否则它必然要经过 \(mid\)。
可以发现,我们可以跑出 \(mid\) 上 \(w\) 个点到这个节点所管理全部节点的最短路,使用 Dij 对一个节点做是 \(\mathcal O(w^2n\log wn)\) 的,整体这一步复杂度应该是 \(\mathcal O(w^2h\log^2h)\)。
询问时看似需要枚举 \(mid\) 列上的两个节点,复杂度 \(\mathcal O(w^2)\)。但实际上我们发现这两个节点中间连起来那一步和直接让走到其中一个节点没有区别。所以我们可以直接使它们在一个节点会合。复杂度 \(\mathcal O(w)\)。
同时我们发现有一种很阴间的情况,就是它走出了节点外再走回来。这种情况它会经过上层的 \(mid\),所以我们要边往下移动区间边计算同时在一边的答案,复杂度还是 \(\mathcal O(w)\)。
因为最短路的性质,任何一种多次穿过 \(mid\) 的路径都可以看成只穿第一次,所以都可以只枚举一个断点。
计算答案时查表就行了。总复杂度 \(\mathcal O(w^2h\log^2h+qw\log h)\)。
QOJ7932. AND-OR closure
人类智慧题。
思路的起点就比较邪门。我们考虑存不存在一些位是耐与王。换句话说,这些位不管怎么与都是 \(1\)。进一步地,我们考虑在一个位为 \(1\) 时其他某些位必然是 \(1\)。这是一种绑定关系。
考虑建图,显然一个强连通分量的状态是相同的,所以可以看成一个位。那么我们可以缩点得到一个 DAG。
考虑这个 DAG 上选择一个点是 \(1\) 的意义:所有它可达的点都必须是 \(1\)。
事实上我们可以证明这个东西自然是传递闭包好了的,换句话说,\(x\) 可以到达的所有点都是直接相连的。仔细想一下就比较显然。
考虑在这个 DAG 上选择一个点集,表示选择这个点集可达的点,把被选择的点所表示的位设置成 \(1\) 就总可以对应到 \(B\) 里面的一个数(显然,刚才的每一步操作都存在对应的操作序列)。
为了构成单射,我们只允许选择一个反链。显然不选择反链的方案总可以缩减成反链(选择一个被另一个点可达的点没有意义),而反链的方案又显然是两两不同的。
最 nb 的事情是我们也可以证明任何一个 \(B\) 里面的数都对应一个反链。证掉这个我们就等于证明了 \(B\) 的大小等于这个 DAG 的反链数量。
Proof by KDT
考虑证明任何一个 \(A\) 里面的数都对应一个反链。显然对反链进行与和或得到的都是反链,所以这等价于任何一个 \(B\) 里面的数都对应一个反链。
考虑 \(A\) 中每一位是 \(1\) 的位,那么被这一位绑定的那些位在 \(A\) 中也必然是 \(1\)。考虑每个 \(1\) 自然都绑定自己,并且 \(A\) 中的 \(0\) 位显然必然不会在任何一个绑定中是 \(1\),所以我们把这些绑定关系或起来就能得到 \(A\) 本身。
因为每个绑定关系已经在 DAG 上体现为选择一个点和它的可达点,或起来就是选择一个点集。那么根据上文已经提过的理论,我们总可以抽象出一个反链。所以 \(A\) 里面的数都可以对应一个反链。
那么我们只需数 DAG 反链数量。这个 DAG 只有 \(40\) 个点。
考虑
[TBC]
CF1418G. Three Occurrences
trick 杂交。
Solution by StayAlone
一眼异或哈希,同种颜色按照 \(x,y,x\oplus y\) 循环赋权值,查询异或和为 \(0\) 的区间。
考虑这样做怎么样会错:一种颜色出现并非恰好三次,而是超过三次。考虑枚举左端点 \(l\),可以发现右端点 \(r\) 单调,使用双指针即可。同时维护区间中每种前缀异或和的出现次数,调整好 \(r\) 后查桶得到区间中 \(s_{l-1}\) 的数量即可。使用哈希表即可做到 \(\mathcal O(n)\)。
Solution by Shunpower
考虑分治,计算跨越的贡献时考虑枚举左侧的左端点,右侧的右端点同样双指针。由于我们只能统计 \((mid,r]\) 产生的贡献,所以需要一个主席树去数 \((mid,r]\) 中 \(s_{l-1}\) 的数量。
Solution by zhy1206
Sp 太蠢了!
首先我们可以不用双指针。通过维护四次后继,再进行后缀 \(\min\),我们可以轻易得出每个左端点最远的右端点。
然后考虑我们只需数确定区间 \([l,r]\) 中 \([l,x],x\in[l,r]\) 是合法区间的数量。
进行一波人类智慧:
我们直接对一种元素哈希。所以我们可以考虑使得所有出现三次或零次的元素贡献 \(0\),其他次数贡献任何值,然后进行“和哈希”,其实就是直接判断和是不是 \(0\)。
现在的问题是我们想知道右边有多少个位置从左往右修改这个贡献会和 \(s_{l-1}\) 相同。
考虑这个哈希是可以左右拼在一起的!在左边,我们把出现一次的元素设置成 \(x\),两次设置成 \(y\),右边就反过来,一次的设置成 \(-y\),两次的设置成 \(-x\)。这样的好处是出现三次的元素拼在一起之后就可以变成 \(0\)!所以我们从中间向两侧这样进行前缀和、后缀和,\(suf_l+pre_r=0\) 是合法的,相当于查询右侧的一个前缀的所有前缀和里有多少个 \(-suf_l\),离线之后拿个桶扫过去就能规避数据结构了。
这个和哈希很弱,显然是可以确定性的。总时间复杂度 \(\mathcal O(n\log n)\)。
Solution by qingbaiqwq
考虑扫描线 \(r\)。
显然应该考虑每个 \(r\) 对 \(l\) 的限制。假设该位置上的所有数最后四次分别出现在 \(a,b,c,d\)。那么该位置可以说明 \(r\) 取这里时 \((a,b]\) 和 \((d,r]\) 都是对这个数合法的 \(l\)。
对于一个 \(r\),全局合法的 \(l\) 应当满足此之前所有数的条件,也就是满足条件的数量应该是已经出现过的数的个数。所以我们对条件做区间覆盖,查询最大值个数即可。显然这个数量应当是最大值。
具体地,考虑此前所有数除了在这个位置才出现的都会对这个位置产生贡献,所以先加过来,然后特殊处理一下这个位置上的数就行。
这样做也是确定性的,并且似乎可以扩展到非常数的出现次数做这个题。时间复杂度 \(\mathcal O(n\log n)\)。
CF659G. Fence Divercity
简单题。
首先显然必然切一个子区间。假设我们可以枚举全部区间,考虑怎么直接 \(\mathcal O(n)\) 统计“每一个栅栏都要切”的方案数。
考虑每个位置上需要切的长度被两侧限制,必须要切到 \(1\) 到 \(\min(a_{i-1},a_i,a_{i+1})-1\) 之间的高度(特别地,\(a_0=a_{n+1}=+\infty\)),并且只要切到这个高度区间就一定合法,因为两侧也必然要切,所以就一定连得起来。
那么我们直接先把所有 \(1\) 删掉(显然这不影响,因为能产生贡献的区间里一定没有 \(1\)),然后对于被 \(1\) 分出来每一段计算:
考虑右侧的 \(\prod\) 可以用逆元做(这也是为什么我们要把 \(1\) 删掉再做)。不妨记前缀积为 \(\{mul_n\}\),那么:
右边的和式与 \(l\) 无关,进行前缀和即可。
于是就做完了。写的时候可以不显式把段分出来,但是就会因为 \(1\) 产生亿些细节问题。其实还不如写分出来每个单独算再求和。。。
CF1650G. Counting Shortcuts
我觉得这题很困难啊……*2100 不会做真的抓狂。
考虑刻画最短路和最短 \(+1\) 路之间的差别。我们发现最短路的走法形如走了一条链满足 \(dis_{x_1=s}+1=dis_{x_2},dis_{x_2}+1=dis_{x_3},\cdots,dis_{x_{k-1}}+1=dis_{x_k=t}\),其中当然 \(x_i\) 和 \(x_{i+1}\) 有边。
考虑最短 \(+1\) 路必然在某个位置不满足这条链的性质。可以发现它必然走向一个 \(dis_{x_{i+1}}=dis_{x_i}\) 的位置,证明比较显然(\(dis_{x_{i+1}}\le dis_{x_i}+1\),但是如果走到 \(<dis_{x_i}\) 的位置最短路就必然要增多不止 \(1\) 了)。
于是我们考虑在这样的边上统计最短 \(+1\) 路的数量。根据证明过程,\(x_i,x_{i+1}\) 两边都走最短路,所以对于这种边把两边的最短路数乘起来求和就行了。
CF1787F. Inverse Transformation
蠢题。显然要用置换环。
显然最后要最小化的那个东西就是置换环的数量。考虑刻画一天的变化:
- 所有偶环以相间的形式分裂成两个等大的半环。
- 所有奇环都不会变,但是元素会移动。因为 \(a_i\) 会变成 \(a_{a_i}\),所以也就是把置换环上两位之后的东西拿过来了,\(i\) 变为指向它两位之后的位置。
考虑奇环第二天,因为第一天变换的存在,所以目前两位之后的位置,实际上是原环四位之后的位置。第三天同理。所以 \(k\) 天之后奇环上第 \(i\) 个元素会变成它之后第 \(2^k\) 个。用 0-index 的环表示法就是 \(c_x\gets c_{(x+2^k)\bmod l}\)。
事实上我们可以发现偶环和奇环的变化其实是一样的。只是偶环每个都变成往后找两个连边之后刚好会断开。
考虑倒推。我们可以把 \(2^q(q\le k)\) 个等长的奇环合并成原序列的一个偶环。注意 \(q<k\) 时需要先对奇环进行逆移动。
[TBC]
P4841. 城市规划
多项式吹克。
图上计数问题,并且还有连通性考虑时,可以考虑每次新加一个点产生的贡献。
假设我们已经计算了前 \(n-1\) 个点的答案 \(f_{1\sim n-1}\),那么加入第 \(n\) 个点一定是连通了若干连通块。考虑计数类递推基本技巧,我们不可能枚举所有划分连通块的可能性,所以应该直接钦定一部分已经完好,只考虑与其中一个连通产生的贡献。我们不妨假设它沟通其他连通块的过程中,连向 \(1\) 所在连通块的边全部消失了。
枚举 \(1\) 所在连通块的大小 \(s\),那么剩下的部分就是 \(n-s\)。考虑 \(n\) 这个点有 \((2^s-1)\) 种方案和 \(1\) 所在连通块相连,两侧标号合并产生的贡献是 \(n-2\choose s-1\)\(^{*}\),所以答案就是:
因为是自己卷自己,分治 NTT 即可 2log。不知道存不存在一种东西做在线卷积。
考虑连通性计数基本技巧:用总数减去不连通的,其中我们钦定 \(1\) 所在连通块是主连通块。具体来说:
这是钦定 \(1\) 所在连通块的大小,剩下的点可以随意。乘上标号系数后,这显然构成了一种对应关系。
注意到 \(f_j\) 和 \(2^{\frac{(i-j)(i-j-1)}{2}}\) 已经卷起来了,所以我们明显应该把组合数拆开。众所周知,组合数实际上也是一个卷积形式。于是:
注意在多项式转化过程中,除了要构造卷积,还要构造同构,同构的才好塞进多项式。
然而你发现现在这个式子还是做不了!因为有附加在卷积外的常数项,如果硬做就要写半在线卷积,除非使用科技否则还是 2log 的。
注意到两侧都有 \(\frac{f_i}{(i-1)!}\) 的形式,所以我们干脆移项,于是有:
考虑构造 \(F(x)=\frac{f_x}{(x-1)!},G(x)=\frac{2^{\frac{x(x-1)}{2}}}{x!},H(x)=\frac{2^{\frac{x(x-1)}{2}}}{(x-1)!}\),用 \(F(x)G(x)\equiv H(x)\pmod M\),直接用 NTT 做多项式乘法逆即可。
$^* $:这个地方我想了好久才彻底搞清楚为什么两边保持相对顺序可以算对。考虑我们从 \(n\) 向它连边的时候是选择子集,那么真正的连边操作就是按照原来的顺序对应位的。其他的标号实际上等价于另一种子图或者同一种子图另一种子集。其实这种感受一下显然的问题不应该想得太清楚对不对。
CF1017G. The Tree
首先显然进行数据结构反演,与其直接操作树,不如看一个点是否可以被祖先中的黑点扩展到。
唯一的不同是需要特殊处理一下子树变白的情况,要覆盖掉之前产生的贡献。还没有完全弄明白。
[TBC]
CF1326E. Bombs
近期做过最牛的 *2400。
考虑显然随着炸弹变多,答案会单调递减。我们考虑直接维护答案是很困难的,不妨换维考虑答案能在怎样一个炸弹的前缀中被取到,只要最后我们后缀 \(\max\) 扫过去就好了。
容易想到从小到大扫描线答案时,合法的炸弹前缀在向前移动,考虑双指针。于是我们只需判断在一个炸弹前缀下,一个答案能否被取到。和大小关系有关可以想到 01 转化,我们把大于等于它的 \(p\) 变成 \(1\),炸弹变成 \(-1\),其他东西(没有炸弹的位置或者小于它的数)都是 \(0\)。考虑我们扫过去的时候,炸弹一定会优先干掉 \(1\),次之干掉 \(0\),所以我们最终答案是否能取到它实际上就是:
- 维护一个变量 \(val\),从左往右 \(val\gets \max(val+a_i,0)\),查询最后 \(val\) 是否 \(>0\)。\(a_i\in\{-1,0,1\}\)。
- 支持单点修改。
考虑询问这个东西的一个充分条件就是存在一个正的后缀和,事实上这是充要的。
Proof by StayAlone & Shunpower
充分性显然。
反证,我们尝试证明存在一个合法序列不存在正的后缀和但最终 \(val>0\)。考虑任何序列都必然存在至少一个开头位置 \(val=0\),我们从最后一个 \(val=0\) 的位置开始考虑。
假设这之后没有发生任何取 \(\max\) 事件,那么最终 \(val\) 就是这个位置上的后缀和,也就 \(\le 0\),所以就是 \(0\),因此不是一个合法序列,矛盾。
假设这之后发生取 \(\max\) 事件,说明这个位置不是最后一个 \(val=0\),矛盾。
原命题得证。
然后随便拿一个线段树支持查询后缀和最大值和单点修改就可以了。时间复杂度 \(\mathcal O(n\log n)\)。
这个题想了我好久,真的只有 *2400 吗。
Chery Cup P14. perm
转逆排列无敌了。
考虑我们对 \(p_n=\{0,1,2,\cdots ,2^{n}-1\}\) 在二进制下刻画操作后下标的变化:
对于下标在 \(x\) 的数:
- \(x\gets x\oplus 2^{n-1}\)。
- \(x\) 在二进制下只截断最低的 \(n\) 位,向左循环移位 \(1\) 位。
因为操作在下标上,考虑我们转逆排列之后操作就是对值操作了就方便很多。显然逆排列的逆序对可以和正排列的逆序对一一对应,数量相等,所以我们转逆排列,这样相当于是对值进行以上的操作。那么显然可以扩展到:
- 整个序列任意一个二进制位 \(\oplus 1\)。
- 整个序列循环移位若干位。
考虑这两个操作很明显是独立的,所以我们先枚举循环移位位数。然后考虑怎么异或让逆序对数量最大化。
考虑每一位显然是独立的:这一位相同的元素总是递归下去变成子问题,与 \(0/1\) 无关。所以我们只需最大化每一位上的贡献递归下去就好。
具体实现上,我们可以对每一种前缀分别统计这一位上变或不变的贡献,最后对变和不变单独求和,取其中最小的就好。这样做再精细实现就是 \(\mathcal O(n^22^n)\) 的。
Chery Cup P15. book
转移比较难想清楚的的区间 dp。
考虑每次操作完新压塌的区间肯定是一个全新的区间,不和之前的区间有交,所以这些区间可以彼此独立,存在一种从一个区间开始往外扩展,最后变成全部的解。于是可以区间 dp。
\(f_{l,r,x}\) 表示压塌了 \([l,r]\),掉下来 \(x\) 个球最少使用的球数,于是转移显然枚举最后一个压塌的书架:
考虑证明最后一维是 \(\mathcal O(\max a_i)\) 的:第 \(i\) 层上至多放置 \(a_i\) 个球(多了不如放在下一层保留一个完整的球同时也能压塌这一层),于是最后掉下来的只有 \(\sum \frac{a_i}{2}+\frac{a_{i-1}}{4}+\frac{a_{i-2}}{8}+\cdots\le \max a_i\)。
直接做复杂度就是 \(\mathcal O(Tn^3V^2)\) 的,复杂度比较逆天,但是卡卡常就是可以过……
[THUWC2018] 城市规划
其实是简单题,想挑战一下 Minimax trick。
首先我们显然可以写出 \(\mathcal O(nV)\) 的简单 dp,因为子树的根节点必然占领一种颜色,所以直接设 \(f_{i,j}\) 表示 \(i\) 子树内除了根节点另一种颜色是 \(j\) 就可以了。
[TBC]
CF1458D Flip and Reverse
刻画。
我们一点思路都没有!怎么办?
考虑常规操作:\(0\) 和 \(1\) 转化成 \(\pm 1\),然后我们发现一个区间 \([l,r]\) 可以操作的充要条件是 \(s_r-s_{l-1}=0\)。那么事实上我们不妨把这个东西刻画到数轴上移动,那么事实上一个区间被我们刻画成一个环。
考虑一次操作之后的区间有什么改变。事实上我们发现就是在沿着环倒着走!
那么干脆把有向移动变成无向边,那么我们任意找一个从原点开始的欧拉路径都是一个合法方案。直接找出字典序最小的欧拉路径就可以了。
可以用精妙的写法和的性质来规避 dfs,意义不大,这里不再赘述了。
P4117 [Ynoi2018] 五彩斑斓的世界
一些数据结构 trick。
考虑区间查询出现次数没有比较好的带修结构,我们考虑分块,然后用一个并查集维护。我们维护整块里面某个数变成了哪个数,然后在并查集上维护数量即可。散块需要进行暴力。
然后注意到非常恶心人的空间限制:即便我们简单完成了修改,我们也无法给每个块都开一个并查集,然后查询。于是考虑更换求和顺序,我们从枚举询问扫块转变成枚举块扫描询问,这样就可以拿一个并查集做完了。
考虑修改怎么做。我们发现:如果 \(x\) 很小,那么很多数都会减掉 \(x\),我们不妨扫描 \(<x\) 的数加上 \(x\),然后给整个块减小 \(x\);如果 \(x\) 很大,那么我们不妨扫描 \(>x\) 的数直接做。
考虑阈值。设该块的最大值是 \(mx\),如果 \(x\le \frac{mx}{2}\),我们进行前者,那么我们可以用 \(\mathcal O(x)\) 的代价使得 \(mx\) 减小 \(x\);反之进行后者,我们可以用 \(\mathcal O(mx-x)\) 的代价使得 \(mx\) 减小 \(x\)。
容易地,考虑后者在 \(x>\frac{mx}{2}\) 时有 \(x>mx-x\),所以后者实际上也是可以直接放到 \(\mathcal O(x)\) 的。均摊下来每块的操作总量是 \(\mathcal O(mx)\) 也就是 \(\mathcal O(V)\) 次的。
注意还有散块我们需要重构。
维护 \(mx\) 的工作需要支持插入删除一种数 \(\frac{Vn}{B}\) 次,也需要查询 \(\frac{qn}{B}\) 次。我们无法简单地维护它。
考虑对于 \(x\le \frac{mx}{2}\) 的修改,我们是可以简单维护的。但是对于 \(x>\frac{mx}{2}\) 的修改,我们若简单地把 \(mx\gets x\),我们将导致 \(mx\) 虚高。考虑证明这样做不影响复杂度:
对于 \(x\) 较小的修改,我们仍然是 \(\mathcal O(x)\) 的;对于 \(x\) 较大的修改,即便出现这种情况,我们也可以通过一次将 \(mx\) 变为新的 \(x\),中间的部分即便是虚空也只做了一次,所以复杂度还是正确的。
事实上也可以利用并查集把虚空扫掉。
这个并查集需要定向合并,所以只能带一只小 \(\log\),但是几乎可以忽略不计了。
于是简单地,我们的修改总复杂度是 \(\mathcal O((qB+\frac{Vn}{B})\log V)\),查询总复杂度是 \(\mathcal O((\frac{nq}{B}+qB)\log V)\)。简单地取 \(B=\sqrt n\) 时复杂度做到大约 \(\mathcal O(q\sqrt n\log V)\)。
然后你就被卡常了。考虑最优化一下我们并查集的写法,因为有合并顺序所以我们可能会牵扯出来版本并查集等一堆很麻烦的东西(还有重构时的清空问题)。
为了方便清空,我们把位置作为并查集的元素(而非值),值作为附加属性。这样带来的好处是值的修改不会产生更多的点。我们在每个并查集的代表元上维护它现在的值,当然反过来我们也需要维护值对应的代表元是谁。
考虑一次合并操作。我们在结构上把它合并过去,然后清掉这个值对应的代表元。就完事了。
P10786 [NOI2024] 百万富翁
没有思路。
我们有两种问出最大值的方式:
- 我们直接 \(1\) 次问掉一个完全图就完事了,坏处是单次问了太多。
- 考虑另一个显然的想法是使用归并排序。我们用 \(\log\) 轮,总共只需要 \(\frac{n}{2}\) 次就能问出来,坏处是轮数太多了。
我会平衡!
归并排序指出,我们没必要一步到位,如果每次折半至多那么 \(\log\) 轮可以把那个人找出来,询问次数会比较健康。
完全图指出,我们没必要慢慢归并,如果对比较小的块应用完全图办法可以一步筛掉超过 \(1\) 个人,这样轮数(也就是分治树树高)会比较健康。
你也可以注意到归并排序的每次询问等价于对一个大小为 \(2\) 的块使用完全图办法。
从而我们考虑扩展归并排序的做法:我们决定每一层分几叉,递归下去做上来的时候内部使用完全图办法,再把分治树树高控制到 \(9\) 以内,并且总的次数控制到 \(1099944\) 以内我们就过了。
可以使用一个 dp,也可以乱搞,也可以手动构造。我觉得可以暴力:考虑底部若干层应该是使用二叉树,然后应该是三叉,后面的使用暴力应该就可以了。
写的时候像正规线段树或者归并排序一样写并不好写。考虑从下往上合并,我们需要把 \(a\) 个元素分块向上合并变成 \(b\) 个,那么就会有 \(a\bmod b\) 个 \(\left\lfloor\frac{a}{b}\right\rfloor+1\),剩下 \(b-(a\bmod b)\) 个 \(\left\lfloor\frac{a}{b}\right\rfloor\),合并上去之后迭代继续做就好了。所以我们实际上需要构造分块数量或者大小数组。用数量应该会好写很多,所以最后是维护了每一层的数量。
用下面的代码枚举叉数反推层数量可以跑出一个 \(s=1099947\) 的解 \([500000,250000,125000,62500,20833,3472,182,1]\):
int br[]={2,2,2,2,0,0,0,0};
int k[10];
int f(int n){
return 1ll*n*(n-1)/2;
}
ll calc(int n,int lvl){
if(lvl==8){
if(n>1) return 1e7;
else return 0;
}
int d=n%k[lvl];
int len=n/k[lvl];
ll ans=calc(k[lvl],lvl+1)+(k[lvl]-d)*f(len)+d*f(len+1);
return ans;
}
int main(){
#ifdef Shun
freopen(".in","r",stdin);
freopen(".out","w",stdout);
#endif
fr1(a,2,30){
fr1(b,2,30){
fr1(c,2,30){
fr1(d,2,50){
fr1(e,2,200){
br[3]=a,br[4]=b,br[5]=c,br[6]=d,br[7]=e;
int n=1e6;
fr1(i,0,7){
n/=br[i];
k[i]=max(n,1);
}
if(calc(1e6,0)<=1099947){
fr1(i,0,7) cout<<k[i]<<",\n"[i==7];
cout<<calc(1e6,0)<<endl;
return 0;
}
}
}
}
}
}
ET;
}
把 \(182\) 改成 \(183\) 就过掉了。好像把最后几个 \(k\) 瞎偏移一下不用按照严格的分叉关系来可以找出来很多附近的解。
P10785 [NOI2024] 集合
小 S 和 小 Y。
看完题我们显然需要尝试先搞出来多项式复杂度的算法。考虑两个集合序列等价的更好的充分必要条件。
如果不能直接撞到正确的条件上,我们将围绕桶产生大量的问题。考虑一个很错的条件:一个区间 \([l,r]\) 合法当且仅当 \([l,r]\) 的每种颜色出现次数桶相同。这显然是错的,因为等价要求所有的映射都一致。
于是考虑一个看起来更对的充分条件:对于区间内任意两个集合,它们合并在一起之后 \(a\) 和 \(b\) 的桶相等。事实上这将通过所有小样例,结合显然的双指针将获得 \(80\) 分。zyl 的假做法和这个做法近似,他成功水过了所有数据。
考虑正解:
一个精妙的条件:考虑一个 \(a\) 中的元素和 \(b\) 中的元素映射在一起意味着它们出现的位置序列至少在 \([l,r]\) 这一段是相同的。那么我们只需维护序列的 hash,然后判定这个 hash 的桶相等就可以了。
沿用双指针的办法。考虑一次移位只会影响 \(3\) 个序列的哈希值。然后考虑我们可以轻易用 \(\sum a_i\times base^i\) 作为权值维护序列 hash,再使用 xor hashing 维护桶哈希,这题就做完了。
实现时需要当心百万 dq 过大江。事实上我们只需要维护序列长度就 ok 了。
注意到任何一个值出现的位置两两不同,于是这个序列哈希事实上等价于桶哈希。进行 xor hashing 会方便很多。
CF1556F Sports Betting
考虑本质是求竞赛图缩点之后链头的期望大小。不妨设 \(f_{i,S}\) 表示考虑点集 \(S\),链头大小为 \(i\) 的概率。
考虑我们每次放入链头,并考虑向后连边产生的贡献,于是有:
\(g_{|T|}\) 表示 \(|T|\) 的导出子图为强连通分量的概率,\(h(T,S-T)\) 表示 \(T\) 中的点都向 \(S-T\) 中的点连边的概率积。
考虑 \(g_{|T|}\) 实际上就是 \(f_{|T|,T}=1-\sum\limits_{i=1}^{|T|-1} f_{i,T}\)。
于是枚举子集后枚举 \(j\),我们可以在 \(\mathcal O(3^n\times n^3)\) 内完成。进一步地发现,计算 \(h\) 可以提出来,并用预处理轻易减小到单次 \(\mathcal O(n)\),转移 \(f\) 用前缀和垒在一起发现就是 \(1\)。
总复杂度 \(\mathcal O(3^n\times n)\)。很简单啊。
事实上应该可以进一步优化规避掉第一维,懒得弄了。
ABC306Ex Balance Scale
水黑。
大小关系显然连边,本质上就是给边定向,问把等于的点缩在一起之后得到 DAG 的方案数。
不妨 dp \(f_S\) 表示点集 \(S\) 满足条件的定向方案数。
先考虑每次删去等于点能不能做。可以发现我们难以计算 \(S\setminus T\) 在加上 \(T\) 之后仍然为 DAG 的方案数。
GellyFish 告诉我们,这时候我们需要考虑每次删去零度点。不妨枚举子集 \(T\) 表示它的零度点实际包含的点集(因为零度点里面有缩过的点)。可以发现实际上真正的零度点数量是 \(\operatorname{cc}(T)\)。
考虑这样显然会算重。注意到任何一个真正的合法方案在删去 \(T\) 的时候都会删去一个它的零度点的子集,相当于钦定原图有至少那么多个零度点。事实上这个感性理解恰好是正确的。
Proof by GellyFish:
事实上这是 DAG 容斥。换句话说,当我们计数 DAG 对删去零度点进行状压 dp 都需要乘这个剥去零度点集产生的容斥系数。
考虑我们的目标是使得任何一个目标 DAG \(G\) 的系数都恰好是 \(1\)。不妨假设 \(G'\subset G\) 的系数都正确(这样我们就可以递推了),那么对于零度点集 \(T\),我们的 \(G\setminus T\) 系数都正确。于是系数只剩下 \((-1)^{|T|-1}\)。这样 \(G\) 的系数也成为 \(1\),对完了。
于是我们直接做子集容斥,把它的贡献干成 \((-1)^{\operatorname{cc}(T)-1}\):
\(\operatorname{cc}(T)\) 可以在外面预处理,用 \(\mathcal O(2^nn^2)\) 轻易取得,于是就 \(\mathcal O(n^22^n+3^n)\) 了。
GYM102759C. Economic One-way Roads
边定向,使得图强连通。
考虑 \(f_S\) 表示点集 \(S\) 强连通的最小代价,然后你就发现转移其实非常困难。它不支持我们一次性加入一个点集。
点集不好加,那就加边集嘛!考虑我们每次往这个强连通图上可以贴一个环或者一条链它还是强连通的(类似耳分解)。当然,我们贴进来的这个东西不能穿过原图,否则就会算重,并且显然在添加环的时候必须有至少两个不在点集中的点参与。
注意到环其实是一条 \(u=v\) 的路径,所以两者我们合二为一。我们考虑 \(g_{S,u,v}\) 表示现在强连通图的点集为 \(S\),我们要加入一条 \(u\to v\) 的路径产生的最小代价。
转移是简单的:
考虑 \(f(S)\),我们可以直接选择 \(u\ne v\) 转移到 \(g(S,u,v)\);也可以选择 \(u=v\),但是我们需要告诉它我们此时不能 \(u\to w\to v=u\),所以我们提前各走一步,转移到 \(u\) 的邻居 \(w_1\),\(v\) 的邻居 \(w_2\),也就是 \(g(S\cup\{w_1\}\cup\{w_2\},w_1,w_2)\)。
考虑 \(g(S,u,v)\),如果 \(u\ne v\),我们需要挑选 \(u\) 的一个邻居 \(w\) 走到 \(g(S\cup\{w\},w,v)\);如果 \(u=v\),那么我们就可以把它加入答案啦。
注意我们在 \(g\) 当中挑选邻居的时候不能选回 \(S\)(其实选回去也没事)。
白大佬 2025/2/10 17:25
耳分解反正只能最优化,你想怎么分解怎么分解。
还有一个小问题:有些边不在这个过程中被添加(因为我们在加边的同时加点,那么有一些边是不参与构成连通性的)。显然这些边可以乱指,所以我们先把所有边往小了指,dp 的时候反转就可以了。
P9870 [NOIP2023] 双序列拓展
学习一下网格图优化 dp。这个题的难度全部在应用这个刻画技巧……
首先剥掉这个题题面里面魔怔的一些表述(比如条件显然是 \(f_i\) 和 \(g_i\) 的关系始终同号),然后就有一个显然的 \(\mathcal O(n^2)\) 东西:我直接把两个数组归并就好了。显然 \(f_{i,j}\) 表示 \(X\) 用到位置 \(i\),\(Y\) 用到位置 \(j\) 是否可行,那么下一步计划显然没必要还停留在 \(i,j\)。向三个方向 \(X_{i+\Delta x_k}<Y_{j+\Delta y_k}\) 的部分走一下就可以了。显然大于号和小于号各自做一遍就好。
这个 dp 根本无法优化。我们考虑刻画它的意义,正如同刻画整体 dp 的数据结构意义。我们在网格图上刻画它,于是我们发现我们的问题转化成查询 \((1,1)\) 能否八连通地走到 \((n,m)\),并且只允许经过 \(X_i<Y_j\) 的点 \((i,j)\)。
特殊性质指示我们思考最小值最大值的问题,其实我觉得直接想到也很合理。不妨先考虑 \(X_\min\),然后我们发现:
- 如果 \(X_\min\ge Y_\min\),那么 \(Y_\min\) 的那一列都全是 \(0\),直接就似完了,根本走不了。
- 反之,我们发现 \(X_\min<Y_\min\) 时,\(X_\min\) 的那一行全是 \(1\),是打通的。
这样的切割让你想到四分树之类有分治结构的东西。似乎我们只要走到 \(X_\min\) 那一行,上下将成为独立的子问题。
- 如果 \(X_\max\ge Y_\max\),那么 \(X_\max\) 那一行类似地直接似完了。
- 如果 \(X_\max< Y_\max\),那么 \(Y_\max\) 那一列类似地打通了。
amazing 啊!此处引用一张经典老图 by @liangbowen:
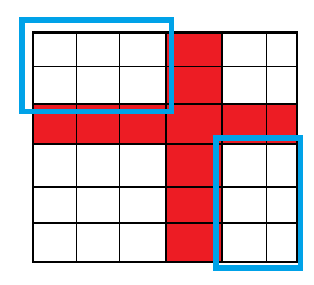
考虑我们只要能判定能否在左上那个矩形里面从 \((1,1)\) 走到边缘,再判定能否在右下那个矩形里面从 \((n,m)\) 走到边缘,就完了。同时可以观察特殊性质,发现实际上特殊性质钦定了打通的部分恰好在最后一行最后一列,也就是要求我们写这个东西的 check 了。
这个东西显然可以递归下去做。我们在矩形里面继续拆卸 \(\min\) 和 \(\max\) 列,将整个矩形将缩小为左上角的矩形(或者鉴定为似完了)。最多缩小 \(n+m\) 次,预处理前缀 \(\min,\max\) 后复杂度是线性的。
写的时候需要注意一点:因为我们只需走到边缘,所以有一行或一列全没了不一定是似完的。我们在拆卸的时候可以先按能拆的方向去拆,每次只拆一个合法的方向,就可以漂亮地递归下去了。
这玩意真的还有 dp 的结构吗?我觉得网格图优化 dp 是不好的名字。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号