Hey Gift：I'M NOT NOT far from GOOD

P6085 [JSOI2013] 吃货 JYY

显然这意味着 \(1\) 所在的连通块存在欧拉回路。欧拉回路指引我们状压点的度数，据此我们容易获得一个 \(\mathcal O(B(n)2^n\text{Poly}(n))\) 的做法，用 \(\mathcal O(B(n))\) 来存储连通性。

考虑我们从一条一条加入边的角度来思考是比较困难的，因为我们不可避免地在过程中需要合并连通块。所以不妨转化成从点的角度思考，这样我们把连通块一个点一个点地塞进去，就不存在问题了。

然后问题就变成了怎么知道关键边有没有加入进去，以及怎么计算这部分贡献。我们不妨简单地把关键边的部分放到最后考虑（先全部塞进去又会需要合并连通块），这样贡献和度数的影响仍然很好算，但最后全部加入的时候连通性会比较麻烦。所以我们在加点的时候，应该认为关键边可以贡献到连通性，但它对答案的贡献是 \(0\)。

所以我们的操作指南就很明确了。我们先把连通块通过每次加点 dp 出来，最后再加入关键边。

考虑这个 dp 怎么写。显然我们同样要维护到奇偶性。但是注意到我们是在加点，所以我们永远只需要维护和 \(1\) 相连的点的奇偶性。于是我们只需要 \(3\) 进制：是否和 \(1\) 连通，和 \(1\) 连通的话还需要维护奇偶性。

因为生成连通块的顺序在状态当中的转移无法确定，所以我们要用最短路算法来转移。

然而这样复杂度比较差。因为如果我们要在 dp 连通块的同时考虑内部加边改变奇偶性的话，复杂度将来到 \(\mathcal O(3^n(n^2+(m+k)))\)，难以通过。但是你发现这是根本不必要的：我们完全可以先把连通块 dp 出来，保留关键边端点和 \(1\) 连通的那些状态，这样连通性就不重要了。我们再用 \(\mathcal O(2^n(m+k))\) 的复杂度做一遍加边改变奇偶性即可。

实现时注意细节，关键边可以用两次也太阴间了。

[GDSOI2019] 送分大水题

题意

给定 $n$ 个 $m$ 维向量，每一维的取值只能是 $1$ 到 $4$ 中的整数。接下来有 $q$ 个询问，每个询问都是这四种询问中的一种：

1. 给定一个向量 \(C\)，问有多少种方法从这 \(n\) 个向量中选出两个不同的向量 \(A,B\)，使得 \(\forall i\in[1,m],\max(A_i,B_i)\le C_i\)。
2. 给定一个向量 \(C\)，问有多少种方法从这 \(n\) 个向量中选出两个不同的向量 \(A,B\)，使得 \(\forall i\in[1,m],\min(A_i,B_i)\ge C_i\)。
3. 给定一个向量 \(C\)，问有多少种方法从这 \(n\) 个向量中选出两个不同的向量 \(A,B\)，使得 \(\forall i\in[1,m],\max(A_i,B_i)\ge C_i\)。
4. 给定一个向量 \(C\)，问有多少种方法从这 \(n\) 个向量中选出两个不同的向量 \(A,B\)，使得 \(\forall i\in[1,m],\min(A_i,B_i)\le C_i\)。

其中，\(C\) 也是一个 \(m\) 维向量，并且每一维的取值也只能是 \(1\) 到 \(4\) 中的整数。

注意这里的不同不是本质不同，而是编号不同。

数据范围：\(1\le m\le 10\)，\(1\le n,q\le 5\times 10^5\)。

先考虑前两个东西显然很好做。考虑向量集合 \(S\) 包含所有 \(\forall i\in [1,m],A_i\le C_i\) 的向量 \(A\)，那么我们任取 \(S\) 中的两个元素都可以记作答案，并且任何 \(S\) 之外的都不能参与答案，不然就倒闭了。所以答案就是 \({|S|\choose 2}\)。

考虑计算 \(|S|\) 是简单的：我们使用变种高维前缀和就行了。

然后考虑后两问怎么做。一个正常的想法是容斥，但是根本过不了。

我们考虑脑筋急转弯，抛弃掉套路的想法。考虑我们能不能求出 \(\max (A_i,B_i)=C_i\) 的 \((A,B)\) 对的数量，如果可以的话我们只需要做一遍高维后缀和就把答案求出来了！

考虑经典技巧 \((i=x)=(i\le x)-(i<x)\)！我们只需要做一遍高维差分就可以了。/xk

关于高维差分怎么做：和高维前缀和一个道理，把加改成减，顺序倒过来就可以了。

CF1765F Chemistry Lab

有点意思。

显然 \(k\) 个人互相独立，最后就是一个人的答案乘上 \(k\) 就行了。于是我们只需考虑一瓶溶液的代价的期望。

先考虑怎么刻画混合溶液之后溶液的代价。我们充分发扬人类智慧，在平面直角坐标系上使用 \((x_i,c_i)\) 表示一瓶溶液，那么它们连线上的点就可以表示它们能混合出的所有溶液！

于是期望的表达也是简单的：就是这条线下面，\(X\) 轴以上的部分的面积再除以 \(100\)。

于是有几个显然的性质：我们所用到的点必然是凸的，因为如果出现了凹点，那么它被凸包完全偏序掉：它可以配出的浓度凸包也可以，并且价格也更高。据此我们也可以轻易说明用三瓶及以上溶液混合出一种浓度是不优的，向凸包的顶点调整可以让线向上走，这样价格就更高。

于是直接按照 \(x\) 排序 dp 即可。如果把凸性加入状态复杂度是 \(\mathcal O(n^3)\)，然而显然不合法不优，于是直接不管凸性 dp 就可以 \(\mathcal O(n^2)\)。

注意乘 \(k\) 要乘在 dp 里面的期望，因为不需要每个人都付一遍合同的钱。

[GDOI2017] 小学生语文题

题意

给定两个字符串 $S,T$，每次可以将 $S$ 中某个字符往前挪到任意位置。求最少步数使得 $S=T$。需要构造方案。

\(1\le S,T\le 2000\)。

这个状态也太难想了。 菜菜主播为什么想不到倒着做呢 X_X。

由于字符往前挪，那么我们考虑倒着做。不妨设 \(f_{i,j}\) 表示 \(S[i:n]\) 匹配上 \(T[j:n]\) 的最少操作次数，这样 \(S\) 中拿出的 \(n-i+1\) 个字符实际上用到了 \(n-j+1\) 个，剩下的 \(j-i\) 个处于拿出状态。不难意识到我们可以知道这 \(j-i\) 个字符都是什么，因为匹配的部分是确定的，后缀中存在的字符也是确定的。

于是转移就很简单了 T_T。

• 如果 \(S_i=T_j\)，那么 \(f_{i,j}\gets f_{i+1,j+1}\)。
• 否则我们考虑我们要把这个 \(S_i\) 拿起来，匹配的长度不变：\(f_{i,j}\gets f_{i+1,j}+1\)。
• 也可以是后面的东西拿到前面来了。我们用后缀和判定一下有没有东西能够拿过来放到 \(j\) 上，如果有的话我们转移 \(f_{i,j}\gets f_{i,j+1}\)。

构造方案并不困难。我们首先记录转移顺序，然后我们就能找到哪些位置是被后面拿起来的东西填上的，也能知道拿起来的是哪些东西。把这些东西记录一下，从前到后地贪心向后找补就好了。

P10652 [ROI 2017] 前往大都会 (Day 1)

菜菜主播想不到最短路图。

考虑先解决必须是最短路的问题，这种对最短路中再选择的问题，我们可以使用最短路图，其中每条边 \(x\to y\) 存在当且仅当 \(dis_y\) 可以由 \(dis_x\) 转移而来。最短路图的好处是在这个 DAG 上任何 \(1\) 到 \(u\) 的路径都构成一条最短路，我们的转移顺序会明确很多。

考虑怎么在 DAG 上解决原来的问题。显然原图上的铁路拿过来除了掰成了很多段以外没有变化，我们可以按照拓扑序和同根铁路进行转移。对于每条铁路，转移形如 \(f_j\gets \max\{f_i+(d_j-d_i)^2\}\)，这个转移显然具有不合法不优的性质。

这个式子显然是斜率优化，我们在 toposort 的同时对于每条铁路开一个单调栈做转移。值得注意的是，这里我们使用 pull 的 toposort 显然会好写一些，我们先把每个点的前驱点单调栈算出，然后在取出这个点的时候枚举进入自己的铁路进行转移即可。

写起来一堆细节，最后我也不想管了特判过了一个点。

CF1418E Expected Damage

喜欢我补集转化毫无前途吗。

组合问题，考虑减少枚举的量，利用不同的顺序或者不同的方案构建方式进行钦定。

不妨简单地考虑每个怪物在多少种方案中产生贡献。

不妨设攻击力 \(\ge b\) 的怪物有 \(x\) 个，剩下的怪物就有 \(n-x\) 个。这个显然是好求的。

然后我们考虑攻击力较大的怪物怎么做出贡献：剩下的 \(x-1\) 个怪物需要有 \(a\) 个放在它前面，前面的 \(a\) 个怪物任意排，后面的 \((x-a)\) 个怪物也任意排。剩下的小怪物还要插进来。于是方案数为：

\[{x-1\choose a}a!(x-a)!{n\choose x}(n-x)! \]

整个式子只与 \(x\) 和 \(a\) 有关，我们可以 \(\mathcal O(1)\) 计算出。这意味着，对于攻击力较大的怪物，它们做出贡献的方案数都是一样的。我们对这部分怪物做一个前缀和就能求出总贡献。

考虑攻击力较小的怪物怎么做出贡献：先把所有大怪物排好，在第 \(a\) 个大怪物后面的 \(x-a+1\) 个空隙里面选一个插进去，再把剩下的 \(n-x-1\) 个小怪物放进这 \(x+2\) 个空来。于是方案数为：

\[x!(x-a+1){n\choose x+1}(n-x-1)! \]

于是这也是一个只与 \(x\) 和 \(a\) 有关的式子，和上面是同理的。

最后除以 \(n!\) 就做完了。

Comet OJ - Contest #10 C-鱼跃龙门

计算最小的 \(i\) 使得 \(n|\frac{i(i+1)}{2}\)。

显然转化为 \(2n|i(i+1)\)。考虑取 \(2n\) 的因子 \(p,q\)，那么我们希望 \(i=ap,i+1=bq\)，于是 \(bq-ap=1\)。

这显然是一个 exgcd 的形式。我们考虑解出一个 \(a,b\)。尝试对 \(a\) 取最小正整数解即可。

然而 \(\mathcal O(T(\sqrt n+d(n)\log n))\) 被卡常无法通过。考虑 \(p\perp q\)，所以 \(p,q\) 中包含的质因子集合不会相交。于是可以做到 \(\mathcal O(T(\frac{\sqrt n}{\ln n}+2^{w(n)}\log n))\)，就可以了。

P11300 [NOISG 2021 Finals] Archaeologist

还有人类能想出来的东西吗？？

满二叉树部分

这部分就有些太精巧了。

考虑满二叉树的好处是，恰好有两棵子树，且大小是相同的。这指引我们考虑一种奇妙的办法：让考古学家在每个点上走和上一个人恰好不一样的路线。从二进制的角度考虑，这实际上类似于倒着深搜：

0000
1000
0100
1100
0010
1010
...

然后考虑怎么让每个人知道上一个人的路线是哪条。因为走一条路无法改变另一条路的状态，我们考虑用三进制去表示它就好了。于是只需要 \(L\ge 2\) 就可以解决。特别地，一层的满二叉树用菊花的做法简单解决即可。

Full Solution

这个好像反倒没那么精妙。

考虑 Sub2 的做法：我们每经过一个点就把计数器加一，当发现这个点的计数器和叶子数量一样多时就设置为 \(N\)，表示以后不用再走了。

考虑我们实际上不在乎它的具体数量，只在乎它是否是满的。所以我们考虑不记录正值而是记录负值，这样可以控制上界。不妨记录其亮度 \(v_i=\max(L-C,0)\)，其中 \(C\) 表示子树当中还未访问的叶子个数。对于 \(v_i>0\) 的部分，我们是清楚地知道它当中还有多少未访问的叶子，于是可以像 Sub2 一样简单地做。对于 \(v_i=0\) 的部分，我们至少知道它绝对没有遍历完成，我们也可以进入它。

现在剩下的问题是对于 \(v_i=0\) 怎么在遍历的同时及时更新 \(v_i\) 的正确值。考虑分类讨论：

• 儿子中有两个节点 \(v_i=0\)，那么由于 \(2L-1\ge L\)，显然 \(v_i=0\)。
• 儿子中有零个节点 \(v_i=0\)，直接算就完了。
• 儿子中有一个节点 \(v_i=0\)，我还不会做。

[TBC]

P3336 [ZJOI2013] 话旧

你的首要任务是读对题。

题的意思其实是，整个折线每次下降就要碰到 \(0\)。于是直接设 \(f_{i,0/1}\) 表示到达点 \(i\) 时前面的折线是向下或向上的方案数。初始我们设置 \(f_{0,0}=1\)。

然后考虑怎么从上一个转移过来。

• \(f_{i-1,0}\)：
  • 考虑向上。此时我们要求 \(y_{i-1}=0\)，因为前面是向下的。
    • 考虑转移到 \(f_{i,1}\)，那么此时中间的长相：
      
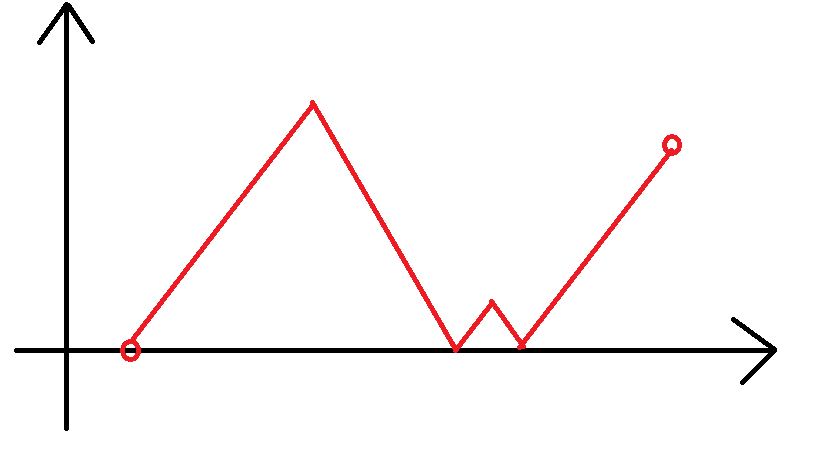
      考虑我们就是要取一个序列 \(P\) 使得 \(2\sum P=x_i-x_{i-1}-y_{i}\)。不妨对 \(\frac{x_i-x_{i-1}-y_i}{2}\) 运用插板，这就是 \(2^{\frac{x_i-x_{i-1}-y_i}{2}-1}\)。特别地，如果 \(x_i-x_{i-1}-y_i=0\)，答案是 \(1\)：我们只有直接向上一种办法了。
    • 考虑转移到 \(f_{i,0}\)，那么此时中间的长相：
      
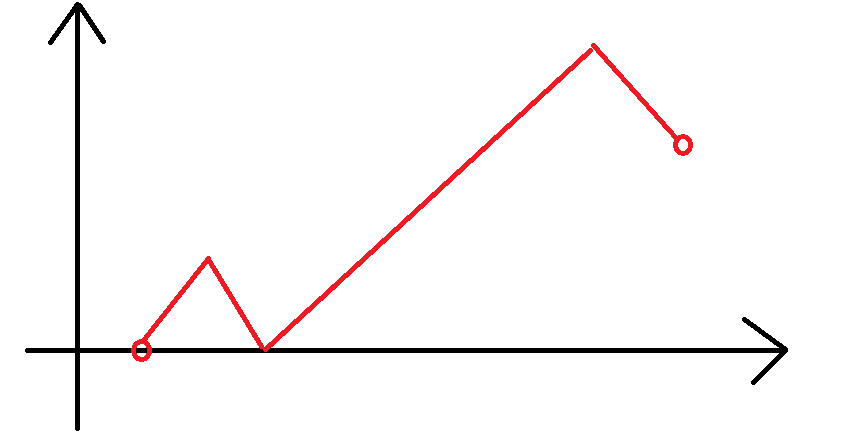
      考虑我们依旧是要取一个序列 \(P\) 使得 \(2\sum P=x_i-x_{i-1}+y_i\)，然而 \(P\) 的最后一个元素需要大于 \(y_i\)。所以我们考虑先把后 \(y_i\) 个元素拨给 \(P_n\)，随后你发现这也是 \(2^{\frac{x_i-x_{i-1}-y_i}{2}-1}\)。
  • 考虑向下。由于我们这个一旦向下就要下到 \(0\)，所以我们本质上是在对 \(x_{i-1}+y_{i-1}\) 做上述的转移。当然，也有可能向下还没下到 \(0\) 就抵达我们要的那个点了，这种特判一下。
• \(f_{i-1,1}\)：
  • 考虑向上。
    • 考虑转移到 \(f_{i,1}\)，那么此时中间的长相：
      
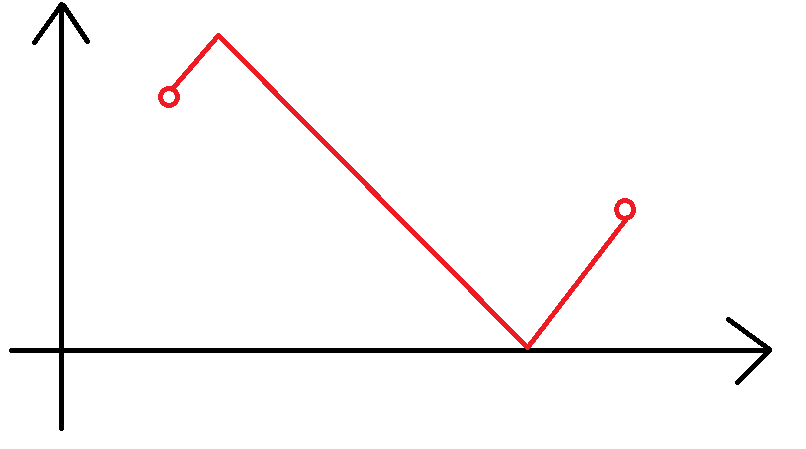
      考虑我们依旧是要取一个序列 \(P\) 使得 \(2\sum P=x_i-x_{i-1}-y_{i}+y_{i-1}\)。特别地，序列的第一个元素需要大于 \(y_{i-1}\)。类似地，我们把前 \(y_{i-1}\) 个元素拨给 \(P_1\)，这是 \(2^{\frac{x_i-x_{i-1}-y_i-y_{i-1}}{2}-1}\)。然而前 \(y_{i-1}\) 个元素也可以是 \(0\) 个元素（直接向下走了），所以这里还要乘一个 \(2\)。
      特别地，如果 \(x_i-x_{i-1}=y_i-y_{i-1}\)，那么我们只有直接向上一种办法了。
    • 考虑转移到 \(f_{i,0}\)，那么我们实际上是要取一个序列 \(P\) 使得 \(2\sum P=x_i-x_{i-1}+y_{i-1}+y_i\)。特别地，序列的第一个元素需要大于 \(y_{i-1}\)，最后一个元素需要大于 \(y_i\)。类似地，我们把前 \(y_{i-1}\) 个元素拨给 \(P_1\)，后 \(y_i\) 个元素拨给 \(P_n\)，这也是 \(2^{\frac{x_i-x_{i-1}-y_i-y_{i-1}}{2}-1}\)。然而前 \(y_{i-1}\) 个元素也可以是 \(0\) 个元素（直接向下走了），所以这里还要乘一个 \(2\)。
  • 考虑向下。由于我们这个一旦向下就要下到 \(0\)，所以我们本质上是在对 \(x_{i-1}+y_{i-1}\) 做 \(f_{i-1,0}\) 出发的转移。当然，也有可能向下还没下到 \(0\) 就抵达我们要的那个点了，这种特判一下。

数数的部分就做完了。注意写的时候一定要想清楚，虽然上面的讨论已经把大部分情况都考虑到了，还是有些细节的小小算重需要考虑一下。重构了一次代码才写出来的第一问。

然后考虑第二问，显然我们可以在第一问的同时 dp 它。只需考虑每种转移能产生的最高点。

LOJ2601.「NOIP2011」观光公交

发现问题具有划分为子结构的性质，考虑贪心。

我们首先要会做 14 年前出现在 NOIP 考场上车人不会做的弱化版。

考虑 dp 后效性起飞，不妨考虑贪心。实际上，我们每一次选择总时间减小最大的位置进行减小是最优的。

Proof.
先假设所有位置都是人等车的。那么对于一个 \(a\to b\) 的乘客，减小 \(b\) 之前的任何一个路段都可以让他的时间减小——要么是在车上的时间减小，要么是车到达的时间减小。
现在考虑车等人。注意到车等人的站台的作用类似把贡献独立出去，我们修改一个车等人站台前面的路段，不会对在车上的终点在这个站台之后的乘客产生影响——他们依然必须坐在车上等人。于是我们先让每个人产生的贡献被车等人的位置切割开来，只有最后一段的一个前缀是有用的。
于是由车等人站台把整个问题划分成了独立的子问题。考虑我们每次实际上就是选择了覆盖次数最多的路段，其实就是某个车等人站台之后的第一个可选站台，因为每个乘客覆盖的是前缀。
我们考虑在产生新的车等人站台之前，显然这样选择是最优的。考虑产生新的车等人站台后，一部分贡献又被切割出去固定掉了。显然，如果我们之前选择了更靠右的站台，失去的可能贡献变多（并且注意到，车等人站台的出现随着路段时间减小是单调的，所以失去了就回不来了），获得的又贡献变少了。所以这样做是正确的。

考虑 \(\mathcal O(n(m+k))\) 怎么写。我们先把每个乘客扩展成一段车等人站台划分出的区间的前缀，只需即时用差分处理出每个段被多少有用的乘客覆盖，支持分裂即可。

然后考虑数据结构。我们可以利用贪心的证明过程中产生的美妙性质来维护。

我们考虑用车等人站台切分路段区间，这样每个乘客占领了一些路段，对这些路段产生贡献。由贪心证明我们知道，这一定是一个路段区间的前缀。

现在考虑我们选择最多的路段直到它之后产生一个位置变成车等人站台。这一块限制可以简单算出并用后缀加法在削减路段时间的同时维护。

主要考虑新增一个车等人站台后对路段被占领次数的影响。考虑对每个人等车站台求出由多少乘客的有效部分将经过这个站台。当这个站台变为车等人站台时，它原本所属的区间的前半截将失去所有经过它的乘客——这些乘客的有效区间被这个站台切割到后面去了。所以这也就是一个区间加法。

使用线段树大力维护即可。细节一车子注意好好处理。

P12461 [Ynoi Easy Round 2018] 星野爱

显然拍扁在序列上，这样我们实际上要做区间颜色权值加，区间颜色权值求和。

然后你发现这就是 CF348C Subset Sums，但没关系我现在又不会了。

考虑分块。把四种贡献拆开算：

• 散块对散块，直接加然后直接查就可以了。
• 整块对查询区间，考虑逐块处理。考虑这之中每个颜色产生的贡献是整块中出现次数和区间中出现次数的乘积，把乘积的和求出来再乘修改的标记就好。考虑把乘积拆在区间上，换句话说，每个颜色的权值是它在整块中的出现次数，然后我们垒一遍前缀和就能求出这个乘积的和了。
• 散块对整块，这和整块对散块是一样的。我们逐块处理，同样的方式可以求出整块与散块区间的交，将一个修改操作转化为普通的询问答案加法。标记打在一整个后缀的查询上。

罴配（bip）

题意

定义一个二分图的点集 $S$ 合法当且仅当存在一个匹配 $T$，使得 $S\subseteq T$。给出一个点带权二分图 $G$，对所有值域内的 $c$ 求有多少个点集的点权异或和为 $c$。

二分图左右部点数量 \(1\le n,m\le 20\)，值域为 \([0,2^{20})\)。

部分分：保证二分图为完全二分图。

首先注意到根据霍尔定理，这意味着我们在左部点或右部点中任取一个 \(\le \min(n,m)\) 大小的集合 \(S\) 都存在 \(\forall T\subseteq S,T\le N(T)\)，就可以以它为基础产生一个匹配。

考虑完全二分图的好处是什么。容易发现只要两边选的点集都满足霍尔定理，我们就可以把两边的点拉出来一起构成一个匹配，换句话说，如果左点集 \(L\) 和右点集 \(R\) 都满足霍尔定理，那么 \(L\cup R\) 也满足。于是左右部分独立，我们对左右各自预处理一遍，使用 FWT 完成异或卷积即可。

然后考虑猜测！显然这个条件具有必要性，所以我们猜测，对于一般二分图这个结论也是充分的，提交发现通过了。

Proof.
设与 \(u\in L\) 相连的点为 \(x_u\)，与 \(v\in R\) 相连的点为 \(y_v\)。不妨按照理想匹配连接边 \(u\to x_u\)、\(v\to y_v\)。那么某个点 \(u\in L\) 不合法，当且仅当 \(\exist v, y_v=u \wedge v \neq x_u\)。
可以证明（但我不会证）此时从 \(u\) 出发总能走到一个终止于右部点（该点不在 \(R\) 中）的增广路，或一个偶环。两种情况都容易进行调整。右部点不合法同理进行调整。调整后边数严格减小，因此调整会停止。

P4339 [ZJOI2018] 迷宫

先转化题意，实际上我们是想设计一种最小的针对 \(m\) 进制数的 DFA，使得有且仅有 \(K\) 的倍数都能走回 \(1\)。

先考虑一种显然的构造：一个包含 \(K\) 个点的 DFA 显然可以满足我们的需求。类似同余最短路，\(i\) 号点的第 \(j\) 条边连向 \((mi+j)\bmod K\) 号点即可（此处点编号是 \(0\)-index）。

然后考虑最小化 DFA。

考虑 Myhill-Nerode 定理：

DFA 中的两个状态 \(u,v\) 等价（即可合并为同一个状态），当且仅当对于所有字符串 \(s\)（可以为空），\(u\) 依次经过 \(s\) 转移到的状态 \(u'\)，与 \(v\) 依次经过 \(s\) 转移到的状态 \(v′\) ，要么同时是接受状态，要么同时不是接受状态。

显然我们的接受状态就是所谓的 \(0\) 号节点，识别了所有 \(K\) 的倍数。

不妨考虑怎样的两个节点出边相同，因为这样的节点显然是等价的，可以首先合并在一起：\(\forall i\in[0,m),um+i\equiv vm+i\pmod K\)，也即 \(um\equiv vm\pmod K\)。特别地，\(0\) 号节点作为接受状态节点不能合并。

感觉上，我们容易得出下面的结论：
根据定理，显然两个状态等价当且仅当我们经过的每个点都满足 \(um\equiv vm\pmod K\)，否则出边不一样的位置就可以用来帮助我们违背等价性。也即等价的节点满足 \(\forall r>0,um^r\equiv vm^r\pmod K\)。

Proof.
不妨记两个节点分别走到了 \(u',v'(u'\neq v')\)，若其中一者为 \(0\) 则得证。否则下一个字符输入 \(K-u'\)，显然串通过 \(u'\) 会被接受，但串通过 \(v'\) 不可能被接受，于是同一个串产生了不同的接受状态，原命题得证。

很遗憾，证明是错误的。谁告诉你 \(K-u'<m\) 了？

实际上解决这个问题和 MN 定理都算不上强相关。因为两个节点出边相同只是判定节点等价的充分条件，下面我们会展示出必要条件是十分复杂的。

考虑我们先进行第一轮缩点，DFA 上的边也同样改变。第一轮缩点结束后，有可能仍然有出边相同的点出现，例如 \(m=2,K=8\) 这个例子：

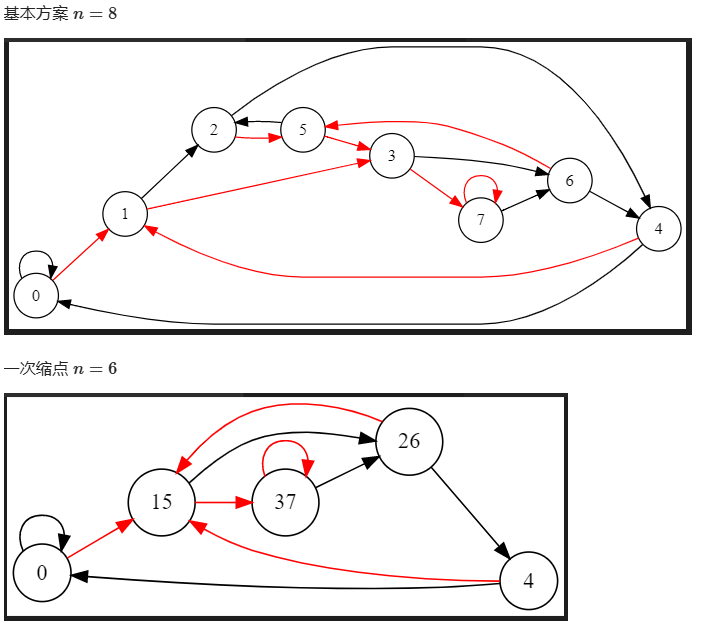
（图片有一处笔误，一次缩点后是 \(n=5\)。）

我们注意到，\((15)\) 和 \((37)\) 由于 \(2,6\) 等价了，所以出边相同了。于是它们又是新的等价节点，需要再缩一次。

我们难以找到必要条件，所以考虑直接模拟这个过程（也不知道为啥是必要的，但感觉很对对吧）。我们每次相当于先寻找一次等价节点，进行合并，之后只把这次合并过的节点迭代到下一次去继续合并（目前还不会证明为啥是对的，但感觉很对对吧）。

考虑 \(um\equiv vm\pmod K\) 这种条件太难受了，实际上它等价于 \(u\equiv v\pmod {\frac{K}{\gcd(m,K)}}\)。

Proof.
懒得证了，记住就行。

这样我们就能写了，因为你发现这个东西的好处是每次递归到下一层时不影响我们的编号，所以我们可以继续把编号记作从 \(1\) 开始的连续值。不妨记 \(f(r,K')\) 表示当前的点编号为 \(1\) 到 \(r\)，模数为 \(K'=\frac{K}{\gcd(m,K)}\)，DFA 里面至少有多少个点（不算 \(0\)）。我们需要的就是 \(f(K-1,K)+1\)。

考虑转移。当 \(r\le K'\) 的时候 \(f\) 显然就是 \(r\)。

搞不清楚了，不想再想了。

CF1646E Power Board / cherykid P107 幂（power）

今天在考场上做出了前一个弱化版的题，然而很遗憾容斥的办法不是很好。= =

不妨钦定 \(x^y\) 总是在最小的 \(x\) 处数到。于是我们不再数任何 \([1,n]\) 之间是其它数幂次的位置。

对于一个不是任何数幂次的位置，它的任何幂次都可以发展一个 \(y\) 出去：形如 \(c^x\le n,y\le m\) 的 \((c^x)^y\)。显然位置之间产生的数是互不相同的。于是我们可以对每一个位置独立数有多少种指数的方案。

于是问题转化为，对所有这样的位置 \(c\)，\(x\le\left\lfloor\log_cn\right\rfloor,y\le m\)，求有多少个不同的 \(xy\)。显然 \(>\sqrt n\) 的部分我们可以简单地解决，考虑 \(\le \sqrt n\) 的部分直接枚举 \(c\) 算出限制之后如何解决。

显然考虑容斥。我们枚举 \(x\) 的子集 \(S\)，考虑有多少个 \(xy\) 能同时整除 \(S\) 子集中所有的 \(x\)，并且除出来最大的数 \(\le y\)。显然可行的 \(y\) 是 \([1,m]\) 之间 \(\frac{\operatorname{LCM}(S)}{\min(S)}\) 的倍数，直接搜即可。然而非常遗憾的是，由于大部分 \(S\) 的 LCM 并没有想象的那么大，所以复杂度倒闭。不过已经可以通过弱化版了。

下面就是题解精妙的地方了。

考虑如果我们没有 \(y\le m\) 的限制，那么我们可以删掉所有是别人倍数的 \(x\)，这样可以直接少一半数，暴力搜索容斥就跑过去了。但问题在于我们不能删，因为 \(<\left\lfloor\log_cn\right\rfloor\) 的数乘上 \(>m\) 的数也可以在 \(\left\lfloor\log_cn\right\rfloor\cdot m\) 以内。

用一个巧妙的办法让这个限制消失。我们不妨按照 \(m\) 分成 \(\left\lfloor\log_cn\right\rfloor\) 块，第 \(i\) 块占据了 \([(i-1)m+1,im]\)。考虑这样分块的好处是，所有 \(x<i\) 的都绝不可能落在这个块里，\(x\ge i\) 的部分如果 \(y>m\) 也落不到块里，我们就可以理所当然地对 \(x\in[i,k]\) 做删掉 \(y\) 的限制的容斥了！由于少了一半数，复杂度可以通过。

P10592 BZOJ4361 isn

显然 dp 这个不降序列，问题在于我们怎样从序列产生一种删除方案。

由于删成不降序列就会立即停止，所以我们希望最后一个删除的数结合这个序列不要是不降的。据此我们容易设计一个 \(\mathcal O(n^4)\) dp：

\(f_{i,j,k}\) 表示前 \(i\) 个数，保留 \(j\) 个数，有 \(k\) 个数可以作为最后一个删除的，于是转移显然：

\[f_{i,j,k}\gets\sum\limits_{p<i\land a_p\le a_i} f_{p,j-1,k-\operatorname{cnt}(p+1,i)} \]

其中 \(\operatorname{cnt}(p+1,i)\) 表示 \((p,i]\) 中 \(<a_p\) 或 \(>a_i\) 的数，这些数显然都可以作为最后一个删除的数，并且其它数显然都不行。

注意把 \(f_{i,j,k}\) 转移出来之后要从序列映射到删除方案，所以要乘 \((n-j)!k\)，特判全选。

从 \(\mathcal O(n^4)\) 到 \(\mathcal O(n^3)\) 是比较简单的。我们把最后一个删除的数塞进状态，在转移的时候顺便就选了，于是 \(f_{i,j,0/1}\) 表示前 \(i\) 个数，保留 \(j\) 个数，是否已经钦定好最后一个删除的数，转移显然：

\[f_{i,j,0}\gets \sum f_{p,j-1,0}\\ f_{i,j,1}\gets \sum f_{p,j-1,1}+\sum f_{p,j-1,0}\cdot\operatorname{cnt}(p+1,i) \]

最终仍然需要乘上 \((n-j)!\)，特判全选。

然而这个 dp 无法继续优化。

考虑容斥。我们考虑抛开那个很烦的限制“删成一个不降序列后会立即停止”，假设可以继续删。这种情况下我们就不在意最后一个数是谁了，于是可以直接转移（注意因为我们关心长度所以还是要加上长度维）：

\[f_{i,j}\gets \sum f_{p,j-1} \]

一层一层做就可以用树状数组优化。

然后考虑怎么从这个到我们想要的东西。考虑设 \(F(i)=\sum f_{p,i}(p-i)!\)，即所有剩余长度为 \(i\) 的“广义”删除方案数，\(G(i)\) 为真正合法的删除方案的数量，不妨钦定一个不合法方案在第一次成为不降序列时候斥掉，容斥之：

\[G(i)=F(i)-\sum\limits_{k=i+1}^n {k\choose i}(k-i)!G(k) \]

UOI 2021

接着 UOI 2021 - Hey Gift：7 hundreds and 20，把这一套先板刷完。

P12579 [UOI 2021] 哥萨克与 GCD

首先考虑 \(\mathcal O(qn^2\log n)\)。我们本质上是用一次代价为 \(\gcd([l,r])\) 的查询查出来了 \(sum_r-sum_{l-1}\)，考虑连边 \(l-1\) 和 \(r\)，于是我们需要一棵生成树才能反解所有 \(sum\)，从而还原序列。

于是用 Kruskal 跑个最小生成树即可。

然后考虑生成树的形态。可以发现生成树一定形如 \(0\) 连接一个后缀，\(n\) 连接一个前缀！显然任何其它边调整成这样都总是不劣的。

于是我们获得了 \(\mathcal O(nq\log n)\) 的做法，每次询问需要重构整个序列的前缀 \(\gcd\) 的后缀和和后缀 \(\gcd\) 的前缀和。

考虑 ds。我们知道，前缀 \(\gcd\) 只有 \(\log\) 段，后缀 \(\gcd\) 也只有 \(\log\) 段，所以两个前后缀和实际上是一个包含 \(\log\) 段的一次函数分段函数。于是所有本质不同的区间只有 \(2\log\) 个，每个区间里面的两坨一次函数是一样的。

于是我们只需查一个区间一次函数最值（两个一次函数的和依然是一次函数），这是简单的。

最后剩下的问题如何维护这些前后缀 \(\gcd\) 段。显然可以用线段树维护 \(\gcd\)，然后在线段树上二分。就做完了。

P12580 [UOI 2021] 猜排列【交互题暂未配置】

没配置不想做了。

P12581 [UOI 2021] 敌人与军刀

简单题，lhttps://www.luogu.com.cn/article/5bonle8s。

UOI 2020

最后一套了！怎么感觉越往前题目风格越正常。 当我没说。

P12633 [UOI 2020] Skyscraper

显然，每一层产生的贡献就是这一层在所有楼里的 \(\max\)，写个 map 累后缀 \(\max\) 即可。

P12634 [UOI 2020] Chessfield

不会，也看不懂题解。

P12635 [UOI 2020] Guess the Color

P12636 [UOI 2020] Array Reduction

P12637 [UOI 2020] Golden Field

简单题。考虑所有数的和为偶数的时候我们直接全部放一起就好了。为奇数的时候，如果 \(n,m>1\) 只需扣掉最小的一个奇数，不影响我们把剩下的东西放到一个位置上；\(n=1\) 时不能乱分，需要分段 dp 一下，也是简单的。

P12638 [UOI 2020] Stone Pairs

这也太难了。

先不考虑 Alice 最后收尾的一步，假设我们的操作是一轮一轮地进行的。那么操作形式只有两种：

• 选择 \((x,x,y,y)\) 四个石子堆，变成 \((x-1,x-1,y-1,y-1)\)。
• 选择 \((x,x,x-1)\) 三个石子堆，变成 \((x-2,x-2,x-1)\)。

从桶的角度上看，某种大小的石子堆数量的奇偶性是不会改变的。所以出现次数为奇数的石子堆自然要贡献一个它的大小，据此我们可以把所有石子堆的出现次数转化为偶数。

考虑我们的操作都具有同一种大小成对减小的特点，不妨除以二成对考虑。假设大小为 \(i\) 的石子堆有 \(b_i\) 对。

考虑只有操作 1 怎么做。可以发现这实际上类似于绝对众数定理：

• \(\max b> \sum b-\max b\)，我们可以利用 \(\max b\) 消去剩下的对，剩余 \(2\max b-\sum b\) 对消不掉。
• \(\max b\le \sum b-\max b\)，类似众数定理，我们对折过去，剩余 \((\sum b)\bmod 2\) 对消不掉。对于这种情况我们发现根本没必要用操作 2，剩的这一对让 Alice 收尾处理一下就好了，所以产生的答案为 \(0\)。

考虑有操作 2 的情况。我们此时可以让 \(\max\) 通过前一个位置，类似跳棋一样每次往前跳两格，尽可能减少消不掉的对产生的贡献。可以证明我们只会跳过那种原本数量为奇数的位置（跳过原本数量为偶数的位置和操作 1 等价），所以最大值往前跳的跳法是固定的。

然后我完全看不懂题解在干什么。

[TBC]

P12639 [UOI 2020] Topological Sorting of a Tree

这其实就是 P4099 [HEOI2013] SAO。

自然地，设 \(f_{i,j}\) 表示 \(i\) 子树内填满，根节点排名为 \(j\) 的方案数，向上树形背包并使用前缀和优化就可以了。注意一下界要取够，不然就被骗了。

P12640 [UOI 2020] Add edges

CF2125E Sets of Complementary Sums

刻画太困难了。

考虑我们不能够直接数序列，因为显然可以多个序列对应同一个集合。

直接大力刻画集合的充要条件较为困难，我们考虑给每个集合钦定一个序列数到它。这样就构成双射了。

考虑每个集合的序列等价类有些什么有性质的东西。通过人类智慧我们发现，一定可以找到唯一一个序列，满足这个序列由至少一个 \(1\) 和一堆互不相同的 \(>1\) 的数组成。

Proof.
不妨假设序列 \(\{a_m\}\) 按从小到大的顺序排好。
假设当前 \(a_1=1\)，但后面有两个相同的数。我们把相同的数展开成一堆 \(1\) 即可。
假设当前 \(a_1\ne 1\)，考虑将所有数减去 \(a_1-1\)，这样 \(a_1=1\) 了。但我们还要让生成的数组不变，而每个数减小 \(a_1-1\) 导致和减小了 \((m-1)(a_1-1)\)，我们在后面塞这么多 \(1\) 就好了。

进一步地容易证明，任何一个集合只存在一个这样的序列。显然一个序列也只能生成一个集合，故双射之。

然后我们考虑怎么数这个 \(\{a_m\}\)。考虑原来的限制放到它身上长什么样：

• 除了 \(1\) 以外还有 \(n-1\) 个互不相同数。
• \(\sum a\le x+1\)。

我们考虑怎么数这样的序列数量。可以发现这本质上就是一个拆分数状物。我们直接设 \(f_{i,j}\) 表示 \(i\) 个数和为 \(j\) 的方案数，运用经典刻画“塞一个或者全加 \(1\)”来生成这个单调递增序列。不妨先删掉头部的 \(1\) 来 dp，转移即为：

\[f_{i,j}\gets f_{i-1,j-i-1}+f_{i,j-i} \]

而 \(\sum a\) 和互不相同数个数之间是经典的根号限制，所以第一维只需 dp 到 \(n\le \sqrt{2(x+1)}\)。

求答案时不要忘记 dp 没有考虑最后加入的 \(1\)，而头部可以加入若干 \(1\)。

P5023 [NOIP 2018 提高组] 填数游戏

这题做得我人不是很好。

首先打一个最暴力的暴力出来，跑出 \(n\times m\le 25\) 的所有结果是不难的。然后我们发现三件事：

• \(n,m\) 和 \(m,n\) 的答案相同。这说明我们只需考虑 \(n\le m\) 和 \(m\le n\) 二者之一了，不妨考虑 \(m\le n\)。
• 对于 \(m>1\) 且 \(n>m+1\) 时，答案为 \(ans(n,m+1)\times 3^{n-m-1}\)。
• 对于 \(n\ge 4\)，我们有 \(ans(n,m+1)=3(ans(n,m)-2^n)\)。

Proof.
不会。

然后考虑计算 \(n=m\) 的解（\(n<4\) 的情况用刚刚那个最暴力的暴力跑出 \(n=m+1\) 即可）。容易发现，由于 \(m\le n\le 8\)，我们实际上只需要做到 \(n\le 8\)，也就是题上面大概 \(80\) 的部分分。

状压需要离谱的性质，考虑直接拿暴力嗯跑。

首先我们需要注意到一个显然的性质：

• 不能存在两格长成下面这样：

..X1...
..0....

否则任何从左上角走到 X 再从 X 出发的两条分叉的路径都会倒闭。

故每个对角线从左下到右上都形如 111111000000，我们考虑枚举每个对角线上这个分割点的位置，枚举复杂度降为 \(\mathcal O(n!)\)。

紧接着考虑如何快速判定。强行 \(\mathcal O(2^{n+m})\) 判定加上上面的枚举会导致我们的暴力需要跑 \(36\) 小时。实际上存在一个判定的充要条件：

Proof.
必要性显然。
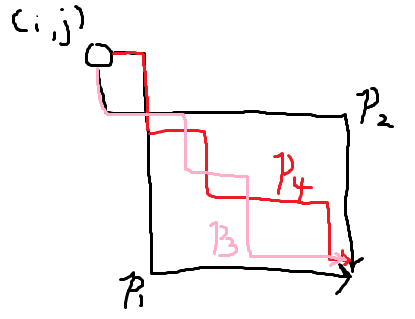
考虑充分性。假设存在一个不合法方案通过上述的判定，不妨考虑所有两条导致不合法的路径 \(p_3,p_4\) 的 LCP 落在的格子 \((i,j)\)，考虑最右下角的一个 \((i,j)\) 上四条路径的形态（钦定 \(w(p_3)<w(p_4)\)）：

由于这是最右下角的一个 \((i,j)\)，换句话说除了这个位置整个右下角的矩形都完全是合法的，于是我们知道 \(s(p_2)\le s(p_3),s(p_4)\le s(p_1)\)。\(w(p_3)<w(p_4)\) 且这两条路径不合法说明 \(s(p_3)< s(p_4)\)，于是 \(s(p_2)<s(p_1)\)。但是 \((i,j)\) 通过了判定，说明 \(s(p_1)\le s(p_2)\)，与假设矛盾。故充分性得证。

这样就简单了。但是如果直接生成出来整个矩形并判定的话依然很慢，不清楚能否在考试时间之内跑出来。但如果一行一行地生成并生成完就判定一行剪枝会快很多，几秒就能跑出 \(ans(8,8)\)。实际上就算没有第三条观察，强行跑出 \(ans(9,8)\) 算出所有 \(n=m+1\) 的情况也只需要几分钟。

P5665 [CSP-S2019] 划分

难受，观察不到。

考虑我们显然希望多分一点，于是容易写出一个最简单的贪心：从前往后扫，能分出来就分出来。

然后你发现这无法通过样例 2，因为中间有个 \(\{4,6,2\},\{13\}\)，虽然 \(\{4,6\}\) 已经足够了，但显然 \(2\) 也应该跟着它们跑。

更一般地，我们发现，如果我们存在数种分段方式，我们必然会选择后半段尽可能短的一种。因为我们知道前半段一定不超过后半段，放进前半段肯定更好，并且这样使得后面的限制更松，不影响前面的限制，所以对答案完全是不劣的。

据此我们维护一个 dp，\(f_i\) 表示前缀 \([1:i]\) 的答案，\(g_i\) 表示前缀 \([1:i]\) 的答案对应的最后一段和，那么利用前缀和数组 \(s\) 转移：

\[f_i\gets f_j+(s_i-s_j)^2\\ g_i\gets s_i-s_j \]

其中 \(j\) 是 \([1,i)\) 中最大的位置使得 \(s_i-s_j\ge g_j\Leftrightarrow s_i\ge s_j+g_j\)。

暴力转移做到 \(\mathcal O(n^2)\)，用任意数据结构找 \(j\) 可以做到 \(\mathcal O(n\log n)\)，但我们想要线性。

注意到 \(s_i\) 是单增的，于是这里有一个浅显的决策单调性。但这个东西和决策单调性的同样问题在于，我们不能用双指针的方式简单地移动它，因为我们不知道在哪里收手。

不过要解决这个问题也是简单的，我们用单调栈维护单调递增的 \(s_j+g_j\) 即可，把正常的二分单调栈换成一个双指针。

然后这个题最恶心的点其实是卡空间。注意到我们找 \(j\) 和 \(f\) 无关，所以没有必要把 \(f\) 这个需要 __int128 的数组存下来。明智的办法是记录转移点，最后重新扫一遍。

P1155 [NOIP 2008 提高组] 双栈排序

我草我咋一个都不会做，流泪了。

考虑从某个角度来说，我们是把整个序列划分成两个序列，使得两个序列都能用一个栈消干净。所以我们考虑一个栈能否被消干净的充要条件。

第一个直觉是取两个数 \(i<j\)，如果 \(p_i<p_j\) 就倒闭。然后你发现这是错误的，比如 1 3 2，那个小的数没有必要留到被大的数占领而出不去。

考虑修正一下这个结论：取三个数 \(i<j<k\)，用小的数 \(k\) 来卡死前面两个数。也就是说，我们不允许 \(p_k<p_i<p_j\)，因为这让我们锁死了 \((i,j)\) 必须先一起进栈，但是进完之后 \(i\) 就不可能比 \(j\) 先出去了，于是条件成立。更好理解的说法是，对于任何一个数 \(x\)，当它入栈时所有当前在栈里比它大的数必须单调递减，这是很好理解的，而当前在栈里比它大的数等价于全局在栈里比它大的数（那些数不可能比它先出去），所以就得到了我们的结论。

据此我们也可以证明该条件充要。

进一步地，我们考虑把这个条件拿回双栈上，发现依然是成立的！只是我们的限制变成了 \(i,j\) 不能放在同一个栈里。更好理解的说法是，对于任何一个数 \(x\)，当它入栈时所有两个栈里比它大的数必须单调递减，同样等价于上述结论。

于是我们可以 \(\mathcal O(n^2)\) 得知所有 \((i,j)\) 是否能在同一个栈中，预处理后缀 \(\min\) 即可。

显然考虑连出一张图，如果不是一个二分图就倒闭了，二分图需要考虑怎么染色分配每个点进哪个栈。显然，对于每个图我们拉出来上面编号最小的点，钦定这个点必须丢进第一个栈，染色即可。

知道分配方案之后为了让字典序最小，还会有一点实现细节，但不是重点。

P5688 [CSP-S2019 江西] 散步

代码能力太差了。重构了一次。

考虑分开维护顺时针的人和逆时针的人，每次我们需要维护每个人到自己最近的可用出口的距离，并支持删除出口。

考虑使用线段树维护。难写题整理一下算法流程：

• 求出最近一个走到出口的人，在两棵线段树上全局 \(\min\) 即可。
• 时间推到这个人走到出口，将这个人设置为离开状态，这个出口的可通过人数减 \(1\)。
• 如果出口消失了，考虑更新所有下一个出口是这个出口的人的下一出口。具体来说，以逆时针为例，找出上一个出口 \(pre\)，下一个出口 \(nxt\)，我们需要将在 \(pre+1\) 到这里之间的人的下一出口设置为 \(nxt\)。这可以通过位置和当前时间回推找出一个环状区间，初始位置在这个区间中的人到出口的距离将进行一个区间加法。

封装一下很快就写好了。注意一下二分写法和重叠取编号最小的细节。

CF2134E Power Boxes

好唐啊，但我怎么又卡住了。

显然可以用三次询问问出 \(a_{n-1},a_n\)，于是我们显然地考虑往前推。

考虑 \(f_i\) 表示从 \(i\) 出发的步数，对于已知的部分我们可以简单 dp 得到。重要的是，考虑两个性质：

Observation 1. \(f_i\ge f_{i+1}\)
Observation 2. \(f_i\ge f_{i+2}+1\)

这说明了一个事实：

Lemma 1. 没有 \(3\) 个相邻相等的 \(f\)。

考虑当 \(f_{i+1}\ne f_{i+2}\) 时，我们询问一次 \(i\) 就行。

当 \(f_{i+1}=f_{i+2}\) 时，我们可以直接自行知道 \(f_i\)，并且这个 \(f_i\) 和这两个数都不相同。于是我们可以直接知道 \(a_{i-1}\)。之后不妨交换 \(i-1\) 和 \(i\)，这样我们再查一次 \(i-1\) 就可以搞出来原本的 \(a_i\) 了。

注意到这个对于 \(i=n\) 也成立，所以不需要单独做最后两个来初始化。需要特殊处理一下 \(i=1\)，这个地方只需要两步就能完成。

显然，这个东西的操作次数在上界内。

CF2134F Permutation Oddness

显然，如果我们把序列划分成奇偶性相同的极长段，设所有段内部的相邻不同的对数总和为 \(i\)，段数为 \(j\)，那么它的 Oddness 就是 \(2i+(j-1)\)。

考虑枚举奇数段数 \(j\)，那么我们将可以知道偶数段数为 \(j-1,j,j+1\) 中的一个。再用两维枚举 \(k,l\)，分别表示奇数段中的相邻不同对数和偶数段中的相邻不同对数，\(\mathcal O(n^3)\) 卷起来即可。

现在考虑怎么计算 \(f_{i,j}\) 表示把奇数/偶数分为 \(i\) 个段，所有段加起来共有 \(j\) 个相邻不同对的方案数。

不要试图 dp 它。这种把一个元素插入另一个元素，dp 至少都需要两维来记录当前数量和 a 的数量导致复杂度过高时，考虑组合计数。

考虑奇数和偶数处的问题等价。我们做奇数处。不妨先把所有 \(1\) 摊开，然后把 \(3\) 插进去。不妨假设 \(3\) 分成了 \(k\) 个极长连续段，插进 \(1\) 的 \(k\) 个空隙中。

这 \(k\) 段的插法也有形态区分（是否放在开头或末尾），不过好在我们总是可以算出这样产生了多少个相邻不同对，假设有 \(l\) 个。

现在开始划分我们意义上的段。我们枚举一下所有段的相邻不同对数量，我们首先要消灭一些相邻不同对，所以要在 \(l\) 个当中选出 \(l-j\) 个，让相邻不同对数降到 \(j\)。

现在还剩下 \(c_1+c_3-1-l\) 个间隔，我们用这些间隔产生划分，让总段数变为 \(i\) 即可。

这样就 \(\mathcal O(n^3)\) 求出了 \(f_{i,j}\)。

P7077 [CSP-S2020] 函数调用

重做这题做得气急败坏，急火攻心了。在 DAG 上要学会刻画，可达性、路径、支配关系都是很重要的。

首先函数之间的调用关系显然是一个 DAG，建图。

然后发现所谓询问的逐次调用没有意义，我们可以直接拿一个主函数把这些过程编成一个函数，也就是建立一个超级源点 \(0\)，依次连向给出的函数。所以本质上我们只执行了这个编号为 \(0\) 的函数。

显然需要转置，我们尝试求出每个加法节点的每一次调用对数组的影响。可以发现，每次调用到一个节点时，我们本质上是想知道之后的乘法标记的乘积，这个乘积乘上这个节点的值代表了这一次对数组对应位置的影响。

故我们只需要求出这个乘积的和。

考虑怎么刻画调用到这个节点的过程，因为我们不可能暴力模拟调用。可以发现，所有调用到这个节点的过程形如从 \(0\) 走到这个节点的一条路径！而这次调用产生的贡献，就是所经过的每个节点上，之后的步骤中的乘法操作的总乘积。换句话说，对于每个出边，我们计算一个 \(suf_i\)，表示在结束这条出边的全部调用过程，回溯到这个节点之后，这个节点上后面的调用产生的乘法操作的总乘积，那么这条路径的贡献就是一路上所有边的 \(\prod suf\)。

考虑如果我们计算好了 \(suf\)，那么直接做一个拓扑 dp 就能算出每个加法节点的贡献系数。现在考虑怎么计算 \(suf\)。

显然考虑计算 \(f_i\) 表示调用一次节点 \(i\) 产生的乘法操作的乘积。那么 \(f\) 的转移是显然的，而 \(suf\) 就只是一个节点上的后缀积。