Hey Gift:7 hundreds and 20
UOI 2021
P12574 [UOI 2021] 机器人
基环树唐题。
P12575 [UOI 2021] 第 k 小的数
元旦激光炮加强版,坏坏坏。
P12576 [UOI 2021] 数字图
败于思路没有回溯性。
显然 DAG 的部分可以简单 dp 取得。
观察 \(1\le a_i\le 2\) 的部分分,想到这个东西大概是黑白染色的样子,A 想尽量停在一种颜色,B 想尽量停在另一种颜色。进一步地我们想到经典 trick,可以把答案二分出来,把大于等于 \(mid\) 的染成 \(1\),小于 \(mid\) 的染成 \(0\),我们希望知道最终能不能取到 \(1\)。
于是只需考虑 \(1\le a_i\le 2\) 怎么做。容易发现对于两个人来说 \(1\to 1\) 和 \(2\to 2\) 这种边都是不想或者不会经过的,所以我们把这种边全部拆掉,问题就转化为在新的图上每次可以移动一步,谁走不动谁倒闭。此外,如果两个人一直走,我们注意到 \(10^{100}\equiv 0\pmod 2\),所以最后也会停在 \(1\) 的位置上,先手还是输了。
所以先手赢当且仅当后手走到 \(0\) 出度点,考虑如何判定这个。注意到此时我们可以拿回 dp 的手法,因为环状转移是明确存在输赢的,我们只需转移赢的过程就可以规避环。我们从 \(0\) 出度点往回拓扑排序,观察 \(f_1\) 就好了。
这里的拓扑排序推状态因为两个人不是公平组合游戏,所以和正常的不一样。考虑一个点 \(0\) 表示先手必输,\(1\) 表示先手必赢。我们往回推的时候要一次推两步,从先手的轮推到先手的轮,再继续下去。
P12577 [UOI 2021] 树上的强盗
唐题这一块/.
考虑把路径拆成两半分开做,我们本质上是想查一条直上直下路径上第一个点 \(i\) 满足:
\(dis\) 表示根到某个点的距离。向下的一侧 \(dis_u-dis_i\) 是反过来的。
这个问题比较难做,考虑拆开第一个条件变成 \(a_i<a_Q\) 和 \(a_Q<a_i\) 做两遍再取较近的一个。这样相当于一个询问有四块问题,每个是找一条直上直下路径上满足某个二维偏序的最近点。我们直接离线第一维比较简单的颜色,然后树剖维护第二维即可。
通过嗯写一下 1log 的线段树上二分可以掉一只 log。
时间复杂度 \(\mathcal O(m\log^2 n)\),常数略大。
P12578 [UOI 2021] 彩色矩阵
没有人会做构造题吧。没有吧?
考虑 \(k\) 是奇数的时候很简单,黑白染色就满足我们的条件。
\(k\) 是偶数,考虑每个点的限制是一个竖着的矩形。我们发挥人类智慧,构造一个类似的形状:
0
000
00000
00000
000
0
上面是 \(k=6\) 处的形状。我们容易发现这个形状本质上就是刻画了那个“竖着的矩形”的边界,它的边界元素之间的距离恰好取到了 \(k-1\) 的上界。
考虑这个形状显然具有可密铺的性质。我们考虑用四种颜色铺开它:
11033333211111033
10003332221110003
00000322222100000
00000122222300000
30001112223330001
33011111233333011
33211111033333211
32221110003332221
22222100000322222
22222300000122222
12223330001112223
11233333011111233
注意到上面这个图形显然存在一个 \(2k\times 2k\) 大小的循环节(我们保留这个大小的矩阵,然后就可以往下面和右边无缝衔接铺出整个矩形了),所以我们生成 \(2k\times 2k\) 大小的子矩形,剩下的部分映射过来即可。
显然这个铺开是满足条件的,恰好两个密铺之间用 \(k+1\) 的长度隔开于是互不影响。容易发现没有少于四种颜色的方案,于是做完了。
UVA12170 轻松爬山 Easy Climb
被 NOIP 模拟赛爆了。
考虑第一个朴素 dp,\(f_{i,j}\) 表示前缀 \(i\) 搞定,第 \(i\) 个数改成 \(j\) 的最小操作次数。于是我们有:
[TBC]
P9340 [JOIST 2023] 旅行 / Tourism
考虑显然我们想要求虚树的节点数量。
一个结论是,虚树的节点数量是所有点按照 dfs 序排序之后,首尾相接地相邻距离之和的一半再 \(+1\)。所以我们可以用莫队加 multiset 维护,做到 \(\mathcal O(m\sqrt q\log m)\),这显然过不了。
一个办法是我们考虑怎么不用 multiset。写一个只删不加的回滚莫队,每次我们在链表上查前驱和后继,\(\mathcal O(1)\) LCA 算距离就好了。
另一个办法是我们抛弃这个刻画:
考虑虚树节点数量的另一种说法:我们把每个点到根路上的点都算进去,考虑这样多了一些,多出来的部分恰好是所有点 LCA 的祖先们。所以我们可以简单地减掉这部分点,只需查询区间 LCA。我们知道这就是区间中 dfs 序最小和最大的两个点的 LCA。
然后考虑怎么计算第一块,也就是有多少个点其子树中包含一个 \([l,r]\) 中出现过的点。显然考虑离线之后扫描线,把询问挂在 \(r\) 上。考虑我们只需要查询树上此时有多少个点其子树内存在一个点在 \(\ge l\) 的时刻出现了。于是我们把点的出现也离线下去,相当于每次对一条链做覆盖,查询全局大于等于某个值的点数。
考虑这个玩意具有 ODT 的性质。由于树剖,我们最多只会产生 \(\mathcal O(m\log n)\) 个区间。在 ODT 上进行暴力覆盖,新增的区间在树状数组上更新即可,注意到覆盖区间只会覆盖若干个整区间和一个前缀,所以 ODT 更是相当地好写。
第一个做法单根,第二个做法 2log。
P5068 [Ynoi Easy Round 2015] 我回来了
很有意思的一道题。
考虑本质上是要查 \(\sum\limits_{i=l}^r\operatorname{mex}_{x\in S}\left\lceil\frac{x}{i}\right\rceil\)。一个想法是考虑维护所有的 \(i\) 在每个时刻的答案,于是查询只需查询区间和。
注意到,因为每个 \(i\) 的答案是由一堆小于等于 \(n\) 的数除以自身上取整后 \(\operatorname{mex}\) 得到的,所以答案单调不降,且的最大值之和只有 \(\mathcal O(n\ln n)\),换而言之,我们可以暴力移动每个点的答案,并同步在树状数组上修改来维护区间和做到 2log。
考虑怎么快速找到需要移动答案的点。
注意到,一个点 \(i\) 需要在时间 \(t\) 移动答案,当且仅当这个 \(t\) 在 \([1,i],(i,2i],(2i,3i],\cdots\) 这些产生不同元素的区间中是一个前缀 \(\max\)。换句话说,这里面每个区间的数一旦出现,就意味着 \(\operatorname{mex}\) 的集合中多了一个数,而前缀 \(\max\) 则意味着 \(\operatorname{mex}\) 能够向后移动的时间点。
注意到这些区间也只有 \(\mathcal O(n\ln n)\) 个,所以我们可以通过遍历它们来得到每个点变化的时间点,在这些时间点向后移动即可。我们需要查询区间当中第一个出现的数是在哪个时间点,ST 表写一个区间 \(\min\) 即可。
总复杂度 2log。
这个东西的正统做法
回到 \(\operatorname{mex}\) 那个地方,我们先对所有 \(i\) 把所有可能的元素插进去,我们每次暴力删除元素,维护还存在的最小值就可以了。显然开 \(n\) 个小根可删堆即可。
于是只需考虑怎么简单地找到需要删除的元素。显然我们每次插入 \(x\) 时只需找到所有包含 \(x\) 的块,这是简单的,用各种数据结构都可以维护。
LOJ #6029. 「雅礼集训 2017 Day1」市场
这 tmd 完全就是 UOJ #228. 基础数据结构练习题。
考虑一直除法会发生什么事情,根据经典结论或者集中注意力可以发现 \(\log\) 次后区间会走向极差为 \(1\) 的道路,极差为 \(1\) 之后再除法可能还是会得到极差为 \(1\) 的区间,就可以类似 UOJ 那个题又加回来就坏了,所以要搞成区间减法。
trickily,我们设置线段树上的节点的 \(\phi=\log(\max-\min)\)。那么考虑每次加法至多导致树上 \(\mathcal O(\log n)\) 个节点的 \(\phi\) 增加 \(\log V\),而每次除法,考虑其操作指南:
- 对于极差 \(>1\) 的区间,递归下去。这将导致这个节点的 \(\phi\) 减小 \(1\)。
- 对于极差 \(=1\) 的区间,如果除法之后极差为 \(0\),递归下去,这个节点的 \(\phi\) 减小 \(1\);否则只是一个区间减法,标记即可。
- 对于极差 \(=0\) 的区间,只是一个区间减法,标记即可。
所以我们每次递归都会导致 \(\sum \phi\) 减小 \(1\),而 \(\sum \phi=\mathcal O((n+q\log n)\log V)\),我们容易知道复杂度是正确的。
CF516D Drazil and Morning Exercise
先用直径理论算出 \(f\),然后我们的问题变成找一个最大的连通块使得 \(\max v-\min v\le l\)。
考虑按照 \(v\) 排序然后双指针滑动窗口过去,那么相当于我们每次需要调整一个点的黑白,求树上最大的黑点连通块大小。不妨使用一个 ddp 状物来算:
\(f_i\) 表示以 \(i\) 为根的最大黑连通块大小,那么 \(f_i=[i \text{ is black}]+\sum\limits_{v\in \text{son}_i} f_j\)。
我们同时维护全局 \(f\) 最大值即可。
注意到和儿子有关的转移,考虑树剖 ddp。我们维护轻儿子的 \(f\) 和为 \(g\),那么 \(f_i=f_{\text{hson}}+g_i\)。考虑每次我们修改一个点,实际上只影响了它到根的链上点的 dp 值。对于连续的重链来说是 \(f\) 发生加法,只有 \(\mathcal O(\log)\) 条轻边上需要特殊处理一下修改轻儿子的贡献,然后继续走重链。
如此维护所有点的 \(f\) 最大值即可。时间复杂度 \(\mathcal O(nq\log^2 n)\)。
然而这过不了。考虑一下 \(f\) 的性质。根据直径性质,我们发现直径的中心就是 \(f\) 最小的点,而如果以这个点为根那么父亲的权值总是小于等于儿子的权值。
考虑我们怎么在递增的树上做这个问题。我们知道,这样永远 \(\min v\) 是最高点,并且其子树内满足条件的点本身一定会构成连通块。所以我们钦定 \(\min v\) 之后只是单纯地希望统计其子树中有多少个点的权值小于等于一个定值。离线下来之后变成链加单点查,差分一次就是单点加区间查了。使用树状数组就能做到 \(\mathcal O(nq\log n)\)。
CF1179D Fedor Runs for President
考虑选中一对点 \(u,v\) 建边之后答案的变化。不妨先假设所有点对都存在恰好一种经过 \((u,v)\) 这条新边的方法,即答案为 \(n(n-1)\),然后我们再考虑减掉做不到的。
考虑拉出 \((u,v)\) 这条链,可以发现,假设我们删掉这条链上的所有边得出了一堆连通块,那么在同一个连通块里面选两个点是做不到经过 \((u,v)\) 的。进一步我们发现这是充要的,容易构造性证明只要选在不同的连通块里就一定可以找到恰好一种办法。
于是考虑 dp,我们期望找出一个删链方案,使得删掉这个链的边集之后得到的连通块 \(siz\) 的 \(\sum {siz\choose 2}\) 最小。
不妨设 \(f_u\) 表示 \(u\) 作为链顶,但认为还要往上的最小答案;\(g_u\) 表示 \(u\) 子树内所有链的最小答案。那么我们转移是简单的:
第三条转移拆开之后是一个 \(g_u\gets \min\limits_{v_1,v_2\in \text{son}_u\land v_1\ne v_2}\{h_{v_1}+h_{v_2}+siz_{v_1}siz_{v_2}\}\) 的形式。把儿子写成序列,可以发现是一个经典的形式,我们可以使用李超线段树解决,也可以使用斜率优化。李超线段树涉及到快速清空和常数问题,所以使用斜率优化会好一点。
答案即 \(n(n-1)-\min g\)。时间复杂度 \(\mathcal O(n\log n)\)。
CF1009F Dominant Indices
本质上即求子树内出现次数最多的第一个深度。本质上我们只要能维护出每个点其子树内每个深度有多少个点就简单了,把这个数组丢到数据结构上维护就行。
那么这个问题是经典的,可以 dsu on tree 也可以线段树合并。发现我以前过了这个题就不写了。
[ARC098F] Donation
赛时想到了 Kruskal 重构树……
考虑捐赠的过程构成一个排列。显然排列之间任意两个点的通行路径都必然是所有路径中经过最大的 \(A_v\) 最小的。据此我们容易想到大根 Kruskal 重构树,这样相当于我们要在这个树上找到一个移动方式,每次移动在树上构成了一条路径,这条路径限制当前剩余的钱数要比 LCA 的权值更大。
注意到这样一件事情:子树之间是独立的。由于越往上权值肯定越大,所以我们不会希望在 \(x\) 子树中移动时在儿子之间横跳,我们会希望儿子里面全部走完之后再上来。
于是考虑 \(f_x\) 表示能将 \(x\) 子树走完,并且最后一个走的是 \(x\) 产生的需要的最少钱数。然后考虑我们需要的是给儿子一个顺序,使得最终这个点的 \(f\) 最小。
然后你发现这样很困难,因为这个子树可能需要加钱来抵达限制,我们无法确知当后面的子树把钱垒起来之后会不会导致前面的消费减少。所以我们聪明地考虑倒着来,把限制改写成 \(c_u=\max(a_u-b_u,0)\),也就是如果到达一个点 \(u\) 有 \(c_u\) 的钱,那么就可以获得 \(b_u\) 的钱。这样无论后面的子树垒起来多了多少钱,对满足限制都是无所谓的。
用这个当作新的权值又回去做。还是相同的状态,贪心一下就好了。懒得写细节了。
P6021 洪水
【模板】动态 dp。
考虑我们 dp 这个东西是简单的,\(f_u\) 表示 \(u\) 子树完成叶子覆盖的最小答案,那么我们的转移形如:
于是考虑 trickily 拿出 \(g_i\) 表示轻儿子的 dp 值之和,那么我们有:
于是在重链上我们的转移形如:
注意这里是 \((\min,+)\) 矩阵。
考虑每条重链的 \(g_i\) 都不变可以直接乘上去,只有 \(\mathcal O(\log n)\) 个点的转移矩阵产生变化。
直接使用树剖 ddp,时间复杂度 \(\mathcal O(n\log^2n)\)。
AT_arc103_d [ARC103F] Distance Sums
考虑树的重心是可以找到的,它的 \(d_i\) 就是最小的那个。
然后我们发现用重心当根有很美好的性质,整棵树上的权值从上到下递增。所以我们知道最大的一定是叶子,并且我们可以做类似剥去叶子的操作,这样不停取得叶子。
问题在于怎么找到叶子的父亲。我们发现在知道一个点 \(siz\) 的情况下我们可以直接换根推理出它父亲的 \(d_i\),所以就能直接找到父亲。而在剥去叶子的过程中,\(siz\) 是可以简单维护起来的。
找到所有点的父亲就相当于把树造出来了。
P5904 [POI 2014] HOT-Hotels 加强版
考虑三个点构成的结构形态一定像一个扇叶状物,所以考虑挂在中间那个交点计数。
那么这时就有两种可能:
- 三个点都在 \(x\) 子树内,是三个不同儿子的同深度点。
- 两个点在 \(x\) 子树内,还有一个在 \(x\) 子树外,其中子树内两个点同深度,子树外那个点到 \(x\) 的距离也是这个值。
考察 \(f_{i,d}\) 表示 \(i\) 子树内距离 \(i\) 为 \(d\) 的点数,\(g_{i,d}\) 表示 \(i\) 子树外距离 \(i\) 为 \(d\) 的点数,那么实际上我们需要算的是:
和
注意到 \(d\) 的上界非常漂亮,只有次长长链的长度大小,而这个大小是允许我们直接枚举 \(\mathcal O(1)\) 次的,因为相当于还是一条长链在链顶算到。所以我们先长剖优化算 \(f_{i,d}\),然后 \(\mathcal O(d)\) 复制出来长链的信息(不能直接改内存池,因为 \(f\) 还要继承上去),剩下的链就可以暴力 dp 了。
然后注意到两个式子其实都没必要分开算。因为向上也可以看成是儿子的一种。
最后剩下考虑怎么计算 \(g_{i,d}\)。这只能直接点分治。
然后开天眼考虑我们有没有简单一点的算法,这一坨东西太难写了。我们考虑换一种枚举方式,我们在这个扇叶状连通块的最高点枚举到它。那么实际上我们做的事情是,在子树内选择一个点,在一个儿子里面选择两个点。
于是不妨设 \(g_{i,d}\) 表示在子树 \(i\) 中选择同深度的两个点,这两个点之间的距离减去深度为 \(d\)。这样这个 \(d\) 就是我们要外挂的一个点的深度。
假设我们每次挂一个子树上去,那么转移是简单的:
可以做到 \(\mathcal O(n^2)\)。
最后整出来长这样:
void dfs(int x,int fa){
f[x].resize(n+1),g[x].resize(n+1);
f[x][0]=1;
for(auto y:p[x]){
if(y==fa) continue;
dfs(y,x);
fr1(j,1,n-1){
ans+=g[x][j]*f[y][j-1];
ans+=f[x][j]*g[y][j+1];
}
fr1(j,0,n-1){
g[x][j]+=g[y][j+1];
if(j) g[x][j]+=f[x][j]*f[y][j-1];
if(j) f[x][j]+=f[y][j-1];
}
f[y].clear(),g[y].clear();
f[y].shrink_to_fit(),g[y].shrink_to_fit();
}
ans+=g[x][0];
// cout<<x<<":"<<ans<<endl;
}
然后显然这个东西需要长剖优化。我们只需要优先走重儿子就能达成继承的效果。于是就做完了。
[ARC103E] Tr/ee
简单题。
考虑显然这个东西需要是一个回文,先把这块判掉。还需要判平凡的 \(s_n=0\) 和 \(s_1=1\)。
然后考虑我们把 \(s_i=s_{n-i}\) 放到小一点的子树 \(i\) 上去构造(不过似乎是无所谓的)。然后把所有需要存在的子树大小(注意还有一个 \(n\))按从小到大顺序排序,容易想到把这些东西搞成一条链,那么我们只是单纯需要给某个点上加一些东西使得它能从上一个大小顶够这个大小。
显然加一堆叶子就行了。
CF1794E Labeling the Tree with Distances
简单题。
考虑假设我们获得了某个点上所有点到它的距离集合,那么考虑给定集合必须和它相差恰好一个 \(\le n\) 的数。
这提示我们使用哈希。我们桶哈这个东西,把所有 \(n\) 种可能的集合塞进 map,然后考虑换根时对每个点取得对应的哈希值,即 \(\sum base^i c_i\),\(c_i\) 表示距离 \(x\) 为 \(i\) 的点数。
显然把 \(base^i\) 当成权值摊开在每个点上,那么每次移动相当于一块点乘上 \(base\),另一块点乘上 \(base^{-1}\)。我懒得搞清楚换根是怎么换的,反正使用线段树换根就能做到 \(\mathcal O(n\log n)\) 了。
好吧还是让我们搞清楚一点
考虑这个东西确实不方便一个数组搞定,考虑拆成两块,\(f_x\) 表示 \(x\) 子树内产生的贡献,\(g_x\) 表示 \(x\) 子树外产生的贡献。
显然我们可以用一次 DFS 搞定 \(f\),有了 \(f\) 之后 \(g\) 的递推也不难了。两块加在一起就是我们要的东西。
[ARC097F] Monochrome Cat
:有什么意思。
考虑显然我们可以先删掉所有黑色叶子,这样所有叶子都是白色的。那么我们就必然要走到这些叶子了,相当于我们需要在树上找一个点开始 dfs。
考虑 dfs 过程产生的贡献。注意到我们走一步就会反一次到达的点,所以叶子恰好会被反一次。扩展开来,我们发现在任何一个完整的 dfs 过程中,任何一个点都恰好会被反 \(deg\) 次。
假设我们的过程是完整的,那么反 \(deg\) 次之后的白色位置就是我们需要应用单独取反的位置,这样是可以简单计算的。
随后我们注意到我们的过程并不是完整的:显然我们可以少走一条回溯的链。换句话说,我们可以取一条链,其上除了其中一端都可以因为不需要走过去而少取反一次。所以不妨先原样将所有点的最终颜色算出来,发现结果就是在原来贡献的基础上,这条链上除了其中一个端点之外,一个白点可以产生 \(-2\) 的贡献,一个黑点可以产生 \(0\) 的贡献。
显然我们希望这条链上端点以外白点最多,但注意到端点一定是黑点,所以直接算完整的整条链就好了。这就是带权直径模板,两遍 BFS 即可。不要忘记加到原贡献上。
HDU6566 The Hanged Man
如何能做起?
题目让选一个体积为 \(\forall x\in[1,m]\) 的独立集使得物品价值最大化。一个简单的想法当然是 \(f_{i,j,0/1}\) 表示 \(i\) 子树内选出体积为 \(x\) 的物品,且 \(i\) 点选或不选的最大物品价值。然而这需要合并背包,\(\mathcal O(nm^2)\) 无法通过。
考虑我们如果能在序列上做这个问题就好了,因为序列上不需要合并背包,只要一个一个选过去就好了。所以我们试图把树拍扁按照 dfs 序直接做,但是你发现这也不行,如果 \(i\) 是叶子,那我们不知道 \(i+1\) 飞到哪个祖先的儿子那里去了,独立集的限制又要求我们必须记录到它的父亲的状态。
如果直接暴力状压链上每个点的状态当然是 \(\mathcal O(2^n)\) 的无法通过。
考虑怎么减少任何一个点到根路径上这种东西的数量。运用人类智慧可以发现树剖的性质就很好,从一个点往上跳轻边的数量是 \(\mathcal O(\log n)\) 的,如果我们能控制到达的祖先永远是重链链底就好了。事实上我们也确实可以做到!
考虑执行轻重链剖分。我们发现重链上的每个点可能有一些叉出去的轻边,而我们不希望跳到这些位置,所以我们的 dfs 序应当优先走轻儿子,再走重儿子。这样虽然破坏了重链一条链上编号连续的性质,但这个性质在这里本来就没什么用。
考虑这样确定 dfs 序之后,当我们走到叶子也即一条重链末端时,这条重链以及重链上所有点的子树肯定已经都完事了,所以下一个点至少都要跳过这条重链,回到上一条重链分叉出来这条重链那个点的位置。进一步地,上一条重链做完之后又要回到上上一条……以此类推。于是我们发现要存储状态的节点都是一些轻边的父亲,且显然总是我们当前所在点的祖先,所以只有 \(\mathcal O(2^{\log n})=\mathcal O(n)\) 的状态。这样就可以做到 \(\mathcal O(n^2m)\) 了。
写起来细节还是有点多的。
JOISC2021 J ビーバーの会合 2 (Meetings 2)
无法战胜日本人。
观察到 \(j\) 为奇数答案总是 \(1\)。事实上这是好证的,我们总是可以朝着多的那边走一步,最后总会停在一个选择的点上,满足两边各有 \(\left\lfloor\frac{j}{2}\right\rfloor\) 个点。
然后考虑偶数的部分。我们延续奇数处证明的思路可以发现,我们也一定只有一条链上的点满足无论往哪边走都恰好有 \(\frac{j}{2}\) 个点,我们想要的就是这条链上的点数最多。注意到显然存在一种方案使得这条链两边一定是两个连通块(除非链长是 \(1\)),所以我们实际上就是想找两个大小恰为 \(\frac{j}{2}\) 个点的连通块,使得这两个连通块之间的最短路径最长。
考虑这很麻烦,因为我们不知道连通块的长相是什么,有可能是一坨向上的东西就很烦。一个办法是尝试点分治,这样我们可以钦定中间那条作为答案的链经过分治中心,然后连通块的形状就很舒服了:因为中间那条链经过根,所以两个连通块就像吊在树上一样,从最高点上看一定都在它的子树里。不过还需要特判连通块占领根的情况。
先在这里按下不表。我们真的需要点分治吗?
考虑我们直接拿重心当根也能确定连通块的形态!因为重心的每个子树大小都 \(\le \left\lfloor\frac{n}{2}\right\rfloor\),而我们想找的连通块最大也就这么大,所以两个连通块的形态一定都是吊在链上的,不可能顺着链向上走,因为如果向上走的话显然可以一路走到根又变成挂着向下的那种形态。
运用一波不合法不优,考虑如果我们直接找两个子树大小 \(\ge \frac{j}{2}\) 的点,这两个点如果构成祖先儿子关系,则之间的距离要么不优要么一个在根也就无所谓了。具体的证明还有几个 \(j\) 比较大的时候的 corner case,但反正是对的。
于是现在我们只是希望找到两个最远的点 \((x,y)\),使得两者的子树大小都 \(\ge \frac{j}{2}\),我们只想要找到这两个点的距离。显然离线之后动态加点,查询点集直径即可。
子序列
题意
给定一对 \(n,k\),求本质不同子序列数量恰好为 \(n\) 的所有 01 串中字典序第 \(k\) 小的。如果不存在输出 \(-1\)。
\(n,k\le 10^9\),采用压缩输出。
完全不会做!刻画了一堆都做不了。
还是回到最开始那一步,我们思考如何计算一个给定 01 串有多少个本质不同子序列。
考虑抛弃一般的本质不同子序列 dp,即 \(f_i\gets 2f_{i-1}-f_{lst_{a_i}-1}\),我们换一种刻画方式。设当前 \(f_0\) 表示 \(0\) 结尾的本质不同子序列数量,\(f_1\) 同理,则当我们往后加一个 \(0\) 时,\(f_0\gets f_0+f_1+1\),反之同理。
这个刻画看起来很反常!但确实是对的。我们这样考虑:考虑现在所有结尾为 \(0\) 的串,我们可以看成是强行钦定所有串的最后那个 \(0\) 都是现在这个位置,往当前的所有串后面塞一个 \(0\)。显然这样我们依然生成出了所有本质不同的串,除了空串转移而来的单个字符。
考虑对 \(f_0\gets f_0+1,f_1\gets f_1+1\),那么可以发现恰好转移也变成了 \(f_0\gets f_0+f_1\)。
考虑这个形式长得像辗转相减法。所以考虑把这个放到 \(\gcd\) 上,如果我们知道最终的 \((f_0,f_1)\),我们可以如下地一一对应回去:
- 如果 \(f_0>f_1\),那么末尾是一个 \(0\),递归到 \((f_0-f_1,f_1)\)。
- 如果 \(f_1>f_0\),那么末尾是一个 \(1\),递归到 \((f_1-f_0,f_0)\)。
- 如果 \(f_0=f_1\),两者等于一个非 \(1\) 的数,那么倒闭了,因为考虑我们不存在两者有且仅有一方为 \(0\) 的状态。但 \((1,1)\) 是一种合法状态,这就是空串。
这意味着,如果最终 \(\gcd(f_0,f_1)=1\) 就有解,否则没有。考虑到 \(f_0+f_1=n+2\),所以实际上无解判断是判断满足 \(\gcd(f_0,n+2)=1\) 的 \(f_0\) 数量。计算出 \(\varphi(n+2)\) 即可。
然后考虑怎么找到字典序第 \(k\) 小。考虑刚刚的构造方式不太方便字典序,我们可以把串翻过来,用相同的方式从头开始构造。
现在我们尝试证明 \(f_0\) 越大的字典序就越小!
考虑两个串 \((f_{0,1},f_{1,1})\) 和 \((f_{0,2},f_{1,2})\)。首先我们知道若 \(\left\lfloor\frac{f_{0,1}}{f_{1,1}}\right\rfloor\ne\left\lfloor\frac{f_{0,2}}{f_{1,2}}\right\rfloor\) 那么显然是较大一方字典序更小,因为那一方 \(0\) 会更多。而这个分数的大小显然可以通过 \(f_0\) 的大小直接比出,就是 \(f_0\) 越大的分数也越大。
然后考虑两者相同会怎样。我们会递归到 \((f_{0,1}-f_{1,1}t,f_{1,1})\) 和 \((f_{0,2}-f_{1,2}t,f_{1,2})\),此时考虑我们依然比较两个分数,发现由于 \(t\) 的部分可以约掉,我们本质上还是在比较 \(\left\lfloor\frac{f_{0,1}}{f_{1,1}}\right\rfloor\) 和 \(\left\lfloor\frac{f_{0,2}}{f_{1,2}}\right\rfloor\)。
归纳而言,我们说明了 \(f_0\) 越大的字典序越小。
所以我们只需找到第 \(k\) 大的 \(f_0\) 满足 \(\gcd(f_0,n+2)=1\) 即可构造出来。显然考虑二分,于是我们只需知道 \(\sum\limits_{i=mid}^{n+2} [\gcd(i,n+2)=1]\),显然莫反即可。
CF1823F Random Walk
树上随机游走。
首先我们显然有一个 \(\mathcal O(n^3)\) 的高斯消元:
在无向图上我们只能做到这个水平。考虑在树上有什么好处。
trickily,我们把式子拆成两块,一块是关于父亲的,一块是关于儿子的,然后把 \(f_u\) 表示为 \(A_uf_{fa}+B_u\),先 dp 出来 \(A,B\),然后从 \(fa\) 开始往下推。
显然我们需要知道根节点的 \(f\)。不妨设 \(f_T=1\) 为根,于是我们对于 \(u\ne T\) 的一般情况有:
现在式子里面只有 \(f_u,f_{fa}\) 了!尝试归一成我们想要的形式:
注意到 \(A_u\) 只关心 \(A_v\),\(B_u\) 只关心 \(A_v,B_v\),所以我们从下到上垒一次系数,然后从上到下垒一遍答案即可。
时间复杂度 \(\mathcal O(n\log p)\),要算那一坨系数的逆元。
CF1610F Mashtali: a Space Oddysey
考虑奇度点(周围所有边的边权和为奇数的点)才有满足条件的可能性,并且无论我们怎么确定方向,对边权和的影响都是 \(0\) 或 \(\pm 2w\),所以奇度点永远都是奇度点。我们尝试达到这个上界,也就是所有奇度点都满足条件。
考虑这样的点长成什么样:
- 奇数个 \(1\),偶数个 \(2\)。直观地,我们希望把它抵消到只有一条 \(1\) 权边。
- 奇数个 \(1\),奇数个 \(2\)。直观地,我们希望把它抵消到两条相反的 \(1,2\) 权边。
假设我们用神力拆掉了这两种边,那么这堆点就成为了偶度点,并且 \(1,2\) 的数量都是偶数,我们就是希望入边和出边可以完全地抵消掉。注意到这是显然可以达成的,我们只需使用欧拉回路,由于欧拉回路具有可以任意选择出边的性质,在每个点上选择与入边边权一样的出边就行了。
然后考虑我们不能拆边怎么办。可以发现还是一样的,我们只需尽量选择一样的就好。但是此时奇度点(这里就是度数为奇数的意思)会比较麻烦,因为我们最后一次定向掉那条 \(1\) 之后就出不去了。所以我们需要造一条无意义的出边,使得图存在欧拉回路。显然我们对于所有奇度点都往一个虚点上连一条边,最后的方案再把虚边拆掉就好了。因为奇度点总有偶数个所以整个图现在都是偶度的,也就存在欧拉回路了。
注意图可能不连通,对每个连通块都跑一下。
CF1137C Museums Tour
考虑一个显然的做法:对于边 \((u,v)\in E\),我们对所有 \(d\) 连接 \((u,d)\to (v,d+1)\)。将每个点上开放日代表的点设置为黑点,这样相当于数 \((1,1)\) 可达的点中有多少种不同的黑点。
考虑 SCC 缩点之后跑拓扑排序。但是你发现这样可能有问题,因为有可能从起点开始走一条链同时能到达两个同种黑点。
Lemma.
同一个博物馆的两个开放时间 \((u,d_1)\) 和 \((u,d_2)\),要么在同一个 SCC 之内,要么不连通。
Proof.
我们只需证明,若 \((u,d_1)\to (u,d_2)\),那么必然有 \((u,d_2)\to (u,d_1)\)。
这意味着 \(u\) 包含在一个环以内。我们不管环长是多少,我们只需要无脑在环上转 \(d\) 圈就能回到原来的 \((u,d_1)\)。那么显然,路上经过的所有 \((u,d_2)\) 满足 \((u,d_1)\to (u,d_2)\),都能做到 \((u,d_2)\to (u,d_1)\)。
于是就没有问题了。我们处理出每个 SCC 中有多少种黑点,直接拓扑就没问题。
注意这题卡空间,手写了一波函数调用栈。/tuu
CF875F Royal Questions
一眼转化,然后变成求最大生成基环森林。
猜测 Kruskal 仍然正确,然后就过了。
Proof.
先考虑为什么树上 Kruskal 是正确的。
考虑取一条非树边 \(e\),考虑其和其两端在树上的路径组成的环,若环上存在一条边 \(e'\) 有 \(w(e')>w(e)\),那么生成树不是最小生成树。
考虑反证,如果真的存在这条边 \(e'\),那么 \(e\) 比 \(e'\) 先枚举到。那么又由于 \(e\) 没有加入生成树,说明 \(e\) 的两端存在一条路径没有经过 \(e'\)。
但 \(e\) 的两端也存在一条路径经过 \(e'\),矛盾。
基环树森林的 case 比较多,懒得写了。
CF1369E DeadLee
哎我真的不会啊。
考虑假设所有人都把两个菜吃了。那么有些菜会吃成负数,我们要补一些回来。
考虑此时如果存在一个菜非负,那么我们可以让吃这道菜的人都放到最后,尽可能避免其他菜的减少。显然地,吃这道菜的人都可以不吃别的是负数的菜了,所以我们可以删去这个点身上的边,另一个点的权值增加。
显然这样贪心是不劣的,我们可以递归到子问题。类似拓扑排序实现即可。
考虑任意时刻如果所有菜都是负数,那么就无解了,因为根本就没法调整,总有一道菜要保持负数,否则在先后关系上就会出现环。
P4229 某位歌姬的故事
Linked to [ABC262Ex] Max Limited Sequence - 触底是会反弹的?触底是会反弹的!。
你说我好吗那我有一点糟。为什么这个想不起来怎么做。
第一步显然,我们对每个数取个上界,问题转化为 \([l_i,r_i]\) 中需要有一个数的权值等于 \(m_i\)。
考虑一个关键但显然的观察:整个 \([l_i,r_i]\) 中只有不可能顶到 \(m_i\)(也即,上界小于 \(m_i\))和上界刚好为 \(m_i\) 的位置!所以我们其实在乎的只有 \([l_i,r_i]\) 中有没有一个上界和自己相同的位置顶到上界了,其他位置我都不关心。
既然其他位置我都不关心,那么显然我可以将每种上界的位置和对应的区间拉出来独立考虑。相当于我们需要在这些位置中选择一些位置填上上界,剩下的位置填 \(lim_i-1\) 的任意数,要求每个 \([l_i,r_i]\) 中有至少一个位置填上上界。
dp 是显然的。\(f_{i,j}\) 表示前缀 \(i\) 当中上一次填入上界的位置是 \(j\) 的方案数。我们把每个限制挂到右端点上,前缀 \(i\) 转移结束之后,对于所有 \(r=i\) 的区间,\(\forall j<l,f_{i,j}\gets 0\)。
考虑我们据此容易获得一个 \(\mathcal O(n^2)\) 的做法。
然后考虑怎么做 \(n\) 奇大无比。注意到绝大部分的点都是没有限制的普通点,我们尝试一个区间一个区间地转移。
考虑把区间拆出来,使得每个区间的限制限制在一堆区间的区间。那么我们可以把区间看成一个新的元素,据此做原问题就可以了。显然拆出的空间是 \(\mathcal O(Q)\) 的。
考虑当区间做元素时产生的贡献:我们从关心元素是否顶到上界转变为关心区间中存不存在点顶到上界,这个方案数依旧是好算的。
使用 ABC262Ex 的办法就能做到 \(\mathcal O(Q\log Q)\),不过原题放过了美好的 \(\mathcal O(Q^2)\)。
CF83C Track
垃圾搜索题
树
题意
给定一棵 \(N\) 个点的树,一条路径的长度定义为它所包含的边数,点到路径的距离是从点到路径上所有点距离的最小值,然后定义路径的高度为所有点到路径距离的最大值。
定义一条极大路径为两个叶子之间的树上路径,求出所有极大路径中长度和高度乘积的最大值,以及取到最大值的极大路径条数,注意 \(A\to B\) 和 \(B\to A\) 是同一条路径。
\(2\le N\le 5\times 10^5\)。
考虑一个正常的想法可能是上 dp 然后长剖优化,类似 P5904 [POI 2014] HOT-Hotels 加强版,但是这个巨大无敌难写,细节还有一车子。
考虑如果我们暴力枚举路径怎么知道距离它最远的点在哪里。如果顺利写出了 \(\mathcal O(n^2)\) 暴力可以发现,我们只要勒令它的一端做根,那么我们在树上简单地预处理一下子树的高度就能知道距离路径最远的点是谁。
每次都换根太愚蠢了!我们考虑怎样能不换根。假设我们随便选一个点做根,那么经过根的路径产生的贡献就是我们刚刚所做的事情:我们在根的两个不同儿子里面取 \(u,v\) 两片叶子,那么我们显然可以预处理出 \(H_u\) 表示根到 \(u\) 路径上的最远点,\(H_v\) 表示根到 \(v\) 路径上的最远点,我们的答案就是 \((d_u+d_v)\times \max(H_u,H_v)\),考虑枚举 \(\max\),然后很容易用任意数据结构维护掉。
问题在于如果我们选到同一个子树里面能不能如法炮制。考虑如果真的乱选一个点,那么我们非常难以刻画距离这条路径最远的点在哪里。
考虑选根时动手脚。trickily,我们尝试选中直径中间那条边当根!(如果有两条边就任选一条均可)
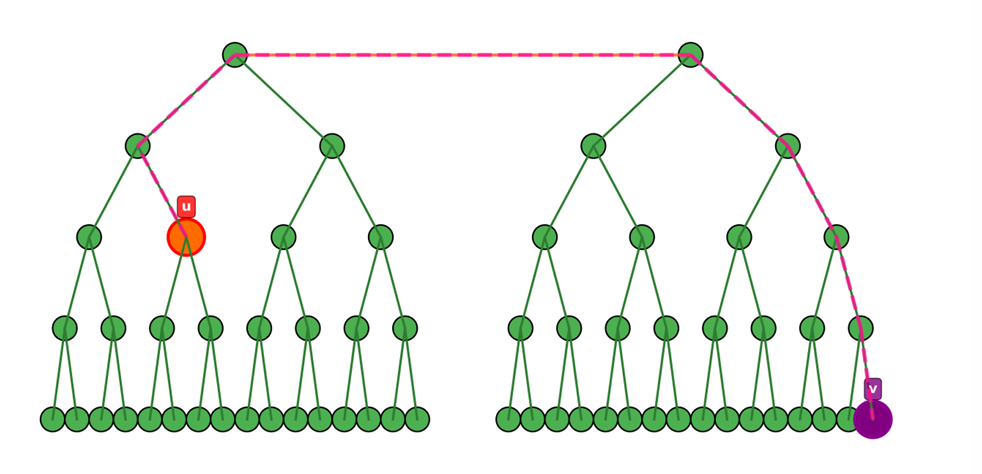
考虑这样之后,我们选中 \(u,v\) 在两边的情况还是类似的。但在相同子树内部选择的性质就漂亮很多了。容易证明,在相同子树内部选择路径 \((u,v)\),距离这条路径最远的点一定是另一个子树的最深点,到这条路径的 \(\text{LCA}\) 的距离就是最远的距离。使用反证法显然。
于是把这种路径挂到 \(\text{LCA}\) 上计数即可,代码并不难写。
CF1905E One-X
技不如人!
本质上我们要对线段树上每个节点 \(i,[l,r]\),计算 \(\sum (2^{r-l+1}-2^{mid-l+1}-2^{r-mid}+1)i\)。
考虑肯定是递归地去数,但是我们发现如果从下向上合并维护标号麻烦得不行,于是换成一层一层数。
既然从下往上有标号的问题,我们就考虑从上往下数!因为从上往下的标号变化是非常简单的,我们已经知道了就是 \(p\to 2p\) 或者 \(p\to 2p+1\)。
但是肯定不能暴力拆开往下数。我们容易注意到,同一种长度的区间产生的贡献是相同的,我们只关心每种长度的标号和。所以我们尝试把每一层长度相同的合并在一起数,于是我们又容易观察到一件事情:线段树上每一层只有两种长度的区间。
然后就做完了。
CF1810G The Maximum Prefix
你说得对但是:

主播怒读错题(以为所有 $p_i$ 都相等),推式子两小时如同白驹过隙:
考虑转成数数,然后再除以概率。
我们不妨钦定,某个数列的分数在第一个最大值处被贡献到。于是我们考虑枚举最大值的位置 \(i\) 和最大值 \(mx\),相当于要求前面的前缀和严格小于 \(mx\),这个位置上严格等于 \(mx\),后面的前缀和不大于 \(mx\)。
不妨先考虑前面,类似 Catalan Numbers,我们就是从 \(0\) 开始走一个 \(i-1\) 步的格路,不允许触碰到 \(mx\),最终走到 \(mx-1\)(因为最后一个一定是 \(1\),我们把最后一个扣了来使得整条格路都满足限制)。
这是格路的数量。考虑我们还容易得知 \(1\) 的数量是 \(\frac{i+mx}{2}\),\(-1\) 的数量是 \(\frac{i-mx}{2}\),所以前面这一块的概率实际上是:
显然此时更好的办法是换元。我们不妨换成枚举最大值位置之前 \(1\) 的个数 \(i\),最大值 \(mx\),那么我们知道这个最大值取到的位置一定是 \(2i-mx\),于是我们前半截的概率可以变成:
然后还需要考虑后面一块的概率。后面也是一个 Catalan Numbers,我们枚举它之后 \(1\) 的个数 \(j\) 有概率为:
合并所有的式子!注意 \(mx=0\) 需要特殊处理:
操作指南已经十分显然,我们考虑枚举 \(d=i+j\),那么:
我们令 \(s\gets 2i-mx\),再进行大力约分:
现在我们知道所有 \(p_i\) 都是不同的,于是组合的办法就倒闭了。考虑 dp 这个东西。
考虑正着做很困难,因为我们需要维护 \(f_{i,j,k}\),表示前缀 \(i\) 的最大前缀和是 \(j\),当前前缀和是 \(k\),然后考虑下一个数填谁。这样做怎么做都是 \(\mathcal O(n^3)\) 的,不能接受。
考虑重新刻画整个问题。最大前缀和就没有别的刻画方法了吗?考虑倒着做,容易发现我们每次往前面加一个数就是直接在调整当前序列的最大前缀和,并插入这一个新的前缀和,我们根本用不着多维护一维当前的前缀和!所以我们倒着维护最大前缀和,每次插入一个数时 \(mx\gets \max(mx+a_i,0)\)。
考虑 \(f_{i,j}\) 表示做了后缀 \(i\),最大前缀和是 \(j\) 的概率,那么我们的转移是:
然而这样又倒闭了,因为我们需要对每个前缀求值,这样搞出来的全是后缀。
考虑怎么解决这个问题。考虑我们每一次只是简单地修改初值的位置,当前缀长度为 \(l\) 时我们简单地取 \(f_{l+1,0}=1\) 作为初值,别的位置都是 \(0\),而转移从来没有变化过。考虑 trickily,我们把整个转移写成一张 DAG,那么注意到每个 \(f_{i,j}\) 到最终 \(f_{1,?}\) 产生的贡献都是一条路径的边权乘积。最终的答案就是 \(f_{1,?}\) 和对应的点权乘在一起,再求和。
考虑现在最开始只有 \(f_{l+1,0}\) 一个位置有值,所以唯一能对答案产生贡献的只有这一个位置。所以我们考虑计算它出发的所有路径的边权乘积乘上终点点权的和。这个显然就是在 DAG 上沿着原来的转移反推了,我们设 \(g_{i,j}\) 表示 \(f_{i,j}\) 处对答案产生的贡献,推到 \(g_{l+1,0}\) 作为答案即可。
也可以从多项式角度理解。我们容易发现由于转移过程固定,所以最终答案可以写成一个关于 \(f_{i,j}\) 初值的大多项式。我们显然可以把这个多项式归一化到同一层上,构成一个 \(ans=F_i=\sum c_jf_{i,j}\)。最终我们可以推到 \(l+1\) 层上,而 \(l+1\) 层上我们只需要 \(f_{l+1,0}\) 的系数。
考虑如何反推系数。显然我们可以轻易获得多项式 \(F_1\),因为我们知道答案就是 \(\sum h_if_{1,i}\)。考虑如何推多项式 \(F_{i+1}\)。
例如转移 \(p_{i-1}f_{i,j}\to f_{i-1,j+1}\),我们知道 \(f_{i-1,j+1}\) 的初值对答案的系数是 \(c_{i-1,j+1}\),那么我们考虑,\(f_{i,j}\) 的初值乘上 \(p_{i-1}\) 之后才能变成 \(f_{i-1,j+1}\) 的初值。所以实际上 \(f_{i,j}\) 的初值获得的系数,相比 \(f_{i-1,j+1}\) 的系数,还要乘上这个转移的系数。另一条转移同理。
车人:

比如我们刚才的 DAG 刻画,把状态的转移变化为初值直接向答案贡献,那么每个状态的初值产生的贡献就是一个路径乘积的和,我们往回推的时候就是在利用乘法分配律,把系数乘给和式的每个项。
CF1117G Recursive Queries
一个想法是建立笛卡尔树,把 \(r-l+1\) 的贡献匀到每个位置上,最后是一个笛卡尔树的深度和。然而我们知道 \([l,r]\) 在原树上只能对应成一个虚树,对这个虚树求解是困难的。
于是抛弃这个想法,考虑直接使用 \(r-l+1\)。注意到在笛卡尔树上,每个点作 \(\max\) 产生的区间,\(r\) 就是右边第一个大于它的数,\(l\) 就是左边第一个大于它的数。当然边界要和询问区间取最值。
单调栈求出两边第一个大于它的数之后简单二维数点即可。
P4463 [集训队互测 2012] calc
多项式刻画 dp 用于优化一类 dp 的其中一维十分巨大,dp 转移简单所以次数增长缓慢的问题。
我们勒令 \(a\) 递增,最后乘一个 \(n!\) 就完事了。不妨设 \(f_{i,j}\) 表示第 \(i\) 位为 \(j\) 的乘积和,那么我们考虑转移:
对这个式子使用前缀和优化,我们直接有:
初值为 \(f_{1,1}=1\)。
然后我们可以归纳地说明,\(f_{i,j}\) 是一个关于 \(j\) 的 \(2i\) 次多项式:
考虑 \(f_{i-1}\) 记为多项式 \(F_{i-1}\),那么我们的转移实际上是说 \(F_i\) 的差分(换句话说,导数)等于 \(F_{i-1}\) 乘一个 \((x+1)\)(注意 \(f_{i-1,j-1}\) 是指 \(j-1\) 在 \(F_{i-1}\) 的点值而非 \(j\) 的),所以 \(F_i\) 的导数的次数比 \(F_{i-1}\) 高一次,那么 \(F_i\) 的次数恰好比 \(F_{i-1}\) 高两次。
我们注意到,\(F_1\) 恰好是一个二次函数(等差数列求和)。所以 \(F_i\) 是 \(2i\) 次多项式,\(f_{i,j}\) 就是这个多项式在 \(j\) 处的点值。
于是考虑我们 dp 出 \(f_{n,1}\) 到 \(f_{n,2n+1}\),就确定了 \(F_n\),再把 \(k\) 处的点值插值出来就行了。
P2791 幼儿园篮球题
理性愉悦一下,简单的推式子题。
我们实际上希望多次求:
考虑分子是难算的,我们想要一个近似于 \(\mathcal O(L)\) 的复杂度。
用第二类斯特林数变化 \(x^L\)。我们有:\(x^L=\sum\limits_{i=0}^{x}{x\choose i}\begin{Bmatrix}L\\i\end{Bmatrix}i!\)。把这个放进去,进行组合恒等变换:
我们用 NTT 计算一行的第二类斯特林数就可以了,时间复杂度 \(\mathcal O(L\log L+SL)\)。
P3266 [JLOI2015] 骗我呢
有空研究 SA 大帝的著作:双射之美——卡特兰数/反射容斥/格路计数。
放弹珠
题目描述
把 $n$ 分拆为 $k$ 个数。$1\le k\le n\le 5000$。考虑正常的 dp 是 \(\mathcal O(n^3)\) 的,因为我们把它刻画成了不降序列,需要维护项数、和、当前最后一个位置的值。
我们考虑压缩状态,换一种可以巧妙地和项数结合在一起的不降序列刻画方式。我们维护当前的不降序列,每次进行两种操作之一:
- 把所有元素加上 \(1\)。
- 在末尾 append 一个 \(1\)。
于是我们利用项数就可以完成转移。\(f_{i,j}\gets f_{i,j-i}+f_{i-1,j-1}\)。
P6189 [NOI Online #1 入门组] 跑步
分拆数。
提米树
题意
有一棵棵提米树,满足这样的性质:每个点上长了一定数量的Temmie 薄片,薄片数量记为这个点的权值,这些点被标记为 \(1\) 到 \(n\) 的整数,其中 \(1\) 号点是树的根,没有孩子的点是树上的叶子。
定义 \((a,b)\) 是一对相邻的叶子,当且仅当没有其它的叶子节点在 DFS 序上在 \(a,b\) 之间。
每对相邻的叶子都会产生一个代价,代价为 \(a\) 到 \(b\) 路径上(不包含 \(a\),\(b\))的点中,最大点权值。
提米树可以提供决心,一棵提米树能提供的决心的数量是树上所有叶子上长的 Temmie 薄片数量和,减去所有相邻叶子的代价。
Temmie 们决定对这棵树进行若干次剪枝(可以不剪枝),使得这棵树能提供的决心最多。
一次剪枝定义为:如果一个点的孩子都是叶子,就可以把它所有的孩子剪掉。
容易发现,我们本质上选择一些点操作就是删掉这个点子树里面除了本身的所有点。
trickily,考虑子树依赖性背包,这个东西使得我们可以简单地按照 DFS 序的顺序转移、跳过子树并维护信息。我们每次有两种选择:
- 跳过整个子树,直接从 \(i\) 转移到 \(i+sz_i\)。
- 进入子树,那么我们需要保留它的儿子。由于我们只允许跳过子树而不允许跳过子树的根,容易证明这个点的儿子都一定会被取到了。
于是我们可以写出一个简单的 \(\mathcal O(n^2)\) dp,因为要维护上一个叶子在哪里来计算共享。
\(\mathcal O(n)\) 还没学。
[ABC416G] Concat (1st)
考虑一个绝大部分正确的贪心:我们直接选择字典序最小的往后面猛接,然后你发现这是错的,比如样例三。因为字典序最小可能是因为构成前缀比较短,这种情况下如果后面还要接一堆那么长的可能会更好使。
考虑如果字典序最小的串不是任何串的前缀,那么我们直接使用它 \(k\) 次就是答案。
否则我们考虑,如果不使用它会使用谁:我们一定会使用包含它作为前缀当中字典序最小的。当然这个也可能有同样的问题,所以我们继续推下去,最终显然只有至多 \(10\) 个串是有用的,并且这些串美好地构成前缀关系。
考虑 \(k\) 很大时,我们显然还是需要使用重复的方法。实际上,我们至少会选择一个串重复至少 \(\max(k-10,0)\) 次(不会证,但是很直觉)。然后考虑在这 \(10\) 个串之后 dp 所有长度下字典序最小的,用恰好 \(\min(k,10)\) 个串拼出的串接上去。接上去之后硬比较就好了。
时间复杂度 \(\mathcal O(|S|^5+n|S|)\)。
AT_joi2020ho_d オリンピックバス (Olympic Bus)
不太难想。
考虑我们会一个 \(\mathcal O(mn^2)\) 的做法:暴力枚举翻边,翻完之后拿 \(\mathcal O(n^2)\) 的 dij 跑一下两边最短路。
这样太垃圾了。考虑最短路树。我们把 \(1\) 开头的,\(n\) 结尾的,\(n\) 开头的,\(1\) 结尾的一共四棵最短路树跑出来,一共只有 \(\mathcal O(n)\) 条边。显然我们应该只有翻转最短路树上的边才需要重跑最短路,于是问题变为快速计算翻转不在最短路树上的边产生的答案。
可以发现是比较简单的,我们用两段路程加起来再加上本边边权就可以求出新的最短路。因为这条边不在任意一棵最短路树上,所以翻转它不会影响两侧的最短路。于是我们去程算一遍回程算一遍加起来就完事了。注意要和原最短路取 \(\min\),因为也可以不经过它。
总时间复杂度 \(\mathcal O(n^3+nm)\)。
CF1186F Vus the Cossack and a Graph
神秘图论题,考虑欧拉回路!结果 zhy 用随机化假算直接过了
考虑每个点保留超过一半的边可以怎样刻画。注意到欧拉回路有美丽的性质:我们可以将入边和出边配对,这样我们只要删去其中一种边就可以了!
但是我们发现这个刻画有点烦人,因为如果我们删了一个点的入边,那么对另一个点来说就是删了出边,我们需要交替地删才对。这启发我们统一一条边对于它两端的意义,显然黑白染色可以满足这个需求。我们把所有黑边都删掉,本质上也是删了一半边。
容易注意到这个产生的界也是正确的:我们最多对所有 \(n\) 个奇度点向超级源点连一条虚边使得所有点(包括超级源点)都是偶度的从而存在欧拉回路,那么我们删掉的真边数至少是 \(\frac{m-n}{2}\)(注意奇点需要都保留了更多的一种颜色,即删掉了虚边的同色边),那剩下的边数自然也就不超过 \(\frac{n+m}{2}\) 了。
然后就是实现细节,因为奇点上我们必须要删掉虚边的同色边,所以简单地取一种颜色删干净是不可行的。我们把整个欧拉回路存下来,用虚边把边集划分开,那么两侧往内第一条边是连在奇度点上的异色边必须保留,再往里就全是偶点其实我们就不关心了,就可以简单隔一个删一个了。
P12621 [NAC 2025] Circle of Leaf
考虑树形 dp,我们维护子树内和 \(1\) 的连通性即可。注意“子树内”包含了若干个连通块,有些连通块因为通过叶子和 \(1\) 相连所以被我们向上断边断掉了,但注意它仍然是我们在这个子树内计算的贡献。当然,我们维护的和 \(1\) 的连通性,只考虑当前和子树根相连的那个连通块。
P7450 [THUSCH 2017] 巧克力
linked to https://www.cnblogs.com/lemonniforever/p/19008366#p7450-thusch-2017-巧克力
P4284 [SHOI2014] 概率充电器
我再也不拆贡献了。条件概率我讨厌你。
首先,答案显然是所有点有电的概率之和。
考虑树形 dp,容易想到起码要设一个 \(f_i\) 表示 \(i\) 通过儿子或者自己使得自己有电的概率。容易发现垒这个是简单的:
容易发现通过这个我们可以计算出根的答案,因为根不需要考虑父亲。于是可以获得美妙的 \(30\) 分。
显然可以换根。我们维护后面一坨乘积为 \(d\),每次从 \(d\) 里面把对应儿子的贡献给除掉,再把父亲的贡献加给儿子即可。
然而儿子的贡献可能是 \(0\),除以 \(0\) 就倒闭了。然而没有关系,我们做过 NOI2025 D2T2,考虑给浮点数扩域,每个数变成 \(x\times 0^y\) 即可。
P13519 [KOI 2025 #2] 通行费
考虑有一个简单的 \(\mathcal O(mn^2)\) 做法,每次暴力重构整张图的最短路。显然过不了。
考虑时光倒流,这样我们的边权只会减小,从而最短路也只会减小,显然维护最短路的减小比增大简单多了。
考虑当边权为 \(0\) 时两个点实际上合并成一个点。如果我们之后在一个“大点”内部合并,显然没有意义。于是有意义的合并只有 \(n\) 次,每次暴力重构最短路即可做到 \(\mathcal O(n^3)\)。
QOJ #7780. Dark LaTeX vs. Light LaTeX
来个正常做法,哈希表太慢了。膜拜绝帆全中国最速哈希表。
不妨钦定我们在 \(S\) 取到 \(ABA\) 这样的串,在 \(T\) 取到 \(B\) 这样的串。另外一种方案就是直接倒过来,不过我们要钦定在某个方向数到 \(A=\emptyset\) 不然就算重倒闭了。
不妨枚举 \(A\) 的开头为 \(i\),\(B\) 在 \(S\) 中的结尾为 \(j\),\(B\) 在 \(T\) 中的结尾为 \(p\)。
考虑我们答案的形态:\(A\) 其实是 \(S\) 中 \(i\) 和 \(j+1\) 开头的一个公共前缀,\(B\) 其实是 \(S\) 中 \(j\) 结尾,\(T\) 中 \(p\) 结尾的一个公共后缀。不妨把这两个东西的最长长度简单 dp 出来,记为 \(f_{i,j+1}\) 和 \(g_{j,p}\)。
那么首先我们需要满足 \(f_{i,j+1}+g_{j,p}\ge j-i+1\)。
通过这里可以发现,我们实际上可以把 \(S\) 中 \(AB\) 的断点放置在 \(f_{i,j+1}\)(如同一个从 \(i\) 开始往右的覆盖)与 \(g_{j,p}\)(如同一个从 \(j\) 开始往左的覆盖)交的任何位置。我们不妨把 \(f_{i,j}\) 在一开始就收缩到不超过 \(j-i-1\),于是我们的贡献形式是:
然后我们看看怎么优化这一坨柿子。
显然我们没有任何必要把 \(f_{i,j+1}\) 带到 \(\min\) 里面。为了方便,不妨设 \(k=j-i+1\),于是:
考虑维护左边,我们希望知道在固定 \(j\) 的情况下有多少个 \(g_{j,p}\) 大于等于某个定值,这显然可以用一个前缀和数组求出。考虑右边的条件实际上是 \(k-1\ge g_{j,p}\ge k-f_{i,j+1}\)(剩下的部分要么做 \(0\) 贡献,要么不满足约束条件),这部分点可以贡献它本身的值减去定值,于是给和再维护一个前缀和数组即可。
平稳套服裁(natlan)
问题其实就是,前 \(k\) 条边加入后 \(u\) 所在的连通块中的点什么时候被一个环串起来。
trickily,这相当于这些点边双连通。边双树,或者其基于的 DFS 树的好处是可以方便地维护合并和加边,而这正是我们想要的。
考虑我们怎么求出这些点边双连通的时刻。考虑维护每个连通块的 DFS 树,显然这个连通块中的点边双连通当且仅当某个时刻这个 DFS 树上的所有边都被别的边覆盖了。感性理解,这个 DFS 树之后无论怎么合并,这一块的结构都不会变化了,而我们知道边双是连续且可以合并的:每次加一条非树边会导致一条链上的所有点合并进边双。所以只要所有树边都在边双里,那么整个连通块里的点也就一定都在边双里了。
于是问题相当于每个边有一个颜色,我们希望维护一个连通块中的颜色之 \(\max\)。这个问题是简单的,先考虑怎么求出颜色。
我们先合并一轮把整个 DFS 树合出来。因为只有这样才能使得我们每个时刻的连通块的 DFS 树都在最后时刻中作为一个子图出现。然后再按顺序扫一遍所有的非树边进行链覆盖就能获得所有的颜色了。
使用树上并查集维护链覆盖即可。
P10644 [NordicOI 2022] 能源网格 Power Grid
零人会做吧。
不妨记一行的和为 \(X_i\),一列的和为 \(Y_i\),我们有 \(C_{i,j}=|X_i-Y_i|\)。
考虑证明当且仅当 \(\sum X=\sum Y\) 时有解。显然这个是必要的,我们只要说明它的充分性即可。
$\sum X=\sum Y$ 时的构造方法
我们考虑在第一行放上所有的 $Y$,最后一列放上所有的 $X$,只有交点拐角那个位置需要特殊考虑。然后我们发现由于 \(\sum X=\sum Y\),所以这个位置可以唯一解出,就构造出来了。
然后考虑我们怎么找出一组满足条件的 \(\sum X=\sum Y\)。
先忽略这个限制,看看怎么让所有 \(X,Y\) 满足 \(C\) 这一块的条件。
不妨取最大的 \(C_{i,j}\),那么产生它的两个数当中必然有一个是最小的,不妨假设是 \(\min Y\)。\(\min X\) 的情况是类似的。
显然我们可以对所有 \(X,Y\) 加上同一个数,不影响满足 \(C\) 的条件。据此我们可以有 \(X,Y\ge 0\),从而刚刚那个 \(C_{i,j}\),我们可以钦定 \(\min Y=0\),然后推知所有的 \(X\)。
于是每一列的 \(Y\) 至多有两种可能(当且仅当所有 \(X\) 都相等时有两种)。注意这里要判断无解。
先考虑任取一种,怎么让它满足 \(\sum X'=\sum Y'\) 的条件。为了不影响 \(C\),我们唯一的办法只有让所有的 \(X,Y\) 全部做加法,所以我们实际上达到的是 \(\sum X+mk=\sum Y+nk\)。这显然等价于 \(n\ne m\) 时 \(\sum X\equiv \sum Y\pmod{n-m}\),\(n=m\) 时 \(\sum X=\sum Y\)。
于是我们想取出满足以上条件的一组 \(Y'\),显然用 bitset 优化 01 背包 dp 即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号