第04次作业-树

 1.学习总结

　　1.1树结构思维导图

　　

　　

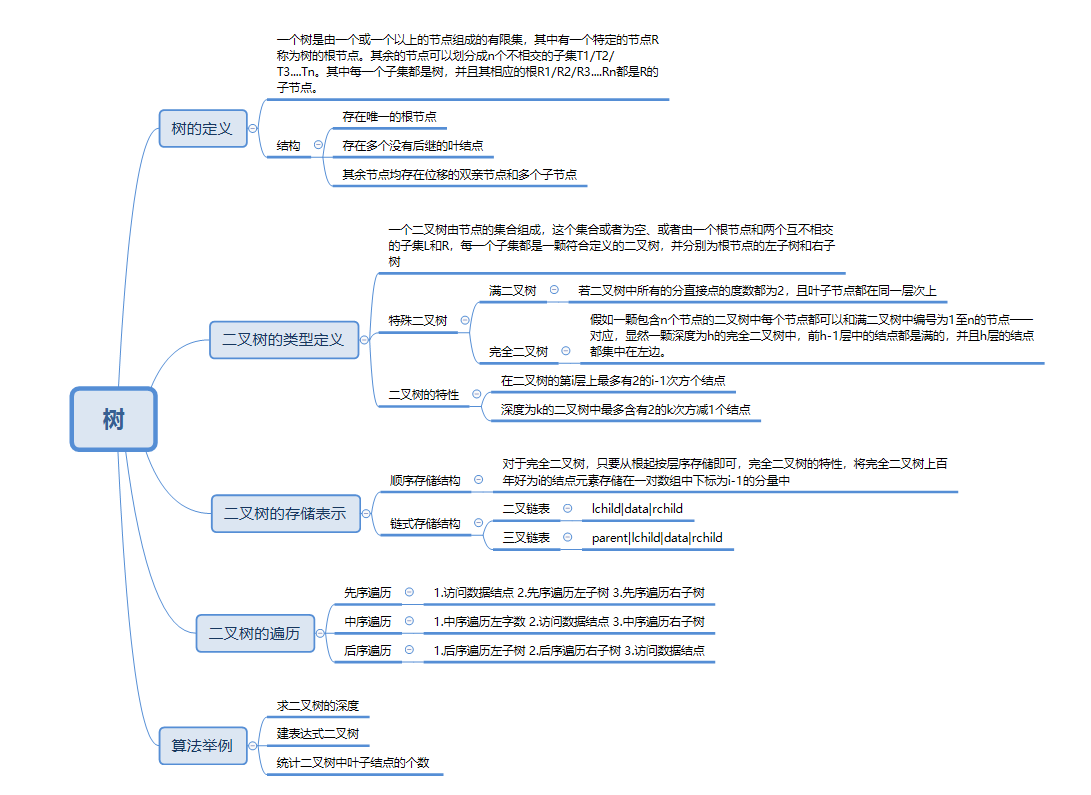
　　1.2 树结构学习体会

　　　　树结构属于非线性数据结构，表示数据之间一对多的关系，是由n个节点组成的有层次关系的集合。树中运用比较重要的就是其递归性质。

　　　　在结构的学习过程中，需要认清树的结构模型，将其转化为实际上的代码，此项是我认为树结构中的难点。

 

　　　　但是相对的，树结构可以解决非常多的问题。最为典型的即计算机中文件系统，而代码应用中可以使用二叉树来解决计算、转换等问题。

---

 

2.PTA实验作业

　　2.1.1 题目1：二叉树操作集

　　　　　　

本题要求用层次法创建二叉树，层次法输入序列是按树的从上到下从左到右的顺序形成，各层的空节点用字符 #表示，如：

 

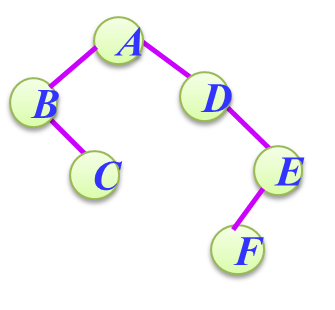
这颗树对应的层次字符串序列为ABD#C#E##F###,即结点的空孩子用#表示。

 

　　2.1.2 设计思路（伪代码或流程图）

　　　　　　

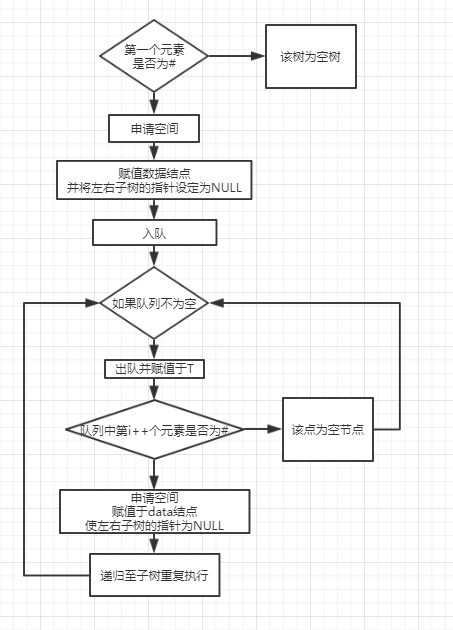
　　2.1.3 代码截图

　　　　

　　2.1.4 PTA提交列表说明

　　　　最后一个字符不带有空格，之后重新编排即可。

---

 

　　2.2.1 题目2：先序输出叶结点

本题要求按照先序遍历的顺序输出给定二叉树的叶结点。

　　2.2.2 设计思路（伪代码或流程图）

　　　　

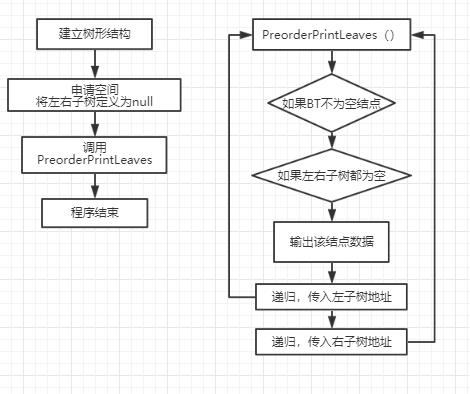
　　2.2.3 代码截图

　　　　　

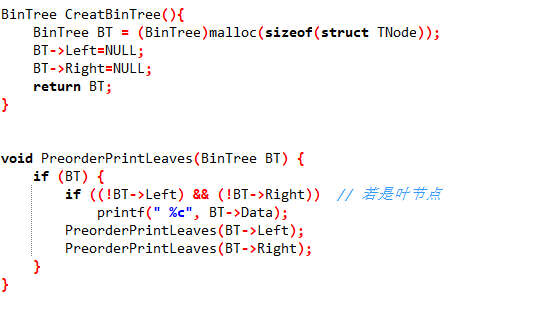
　　2.2.4 PTA提交列表说明

　　　　较为简单，一次通过。

---

 

　　2.3.1 题目3：jmu-ds-表达式树

输入一行中缀表达式，转换一颗二叉表达式树，并求解.
表达式只包含+，-，*，/，（，）运算符，操作数只有一位，且为整数(有兴趣同学可以考虑负数小数，两位数做法)。按照先括号，再乘除，后加减的规则构造二叉树。
如图所示是"1+(2+3)*2-4/5"代数表达式对应二叉树，用对应的二叉树计算表达式的值。 转换二叉树如下：

 

 

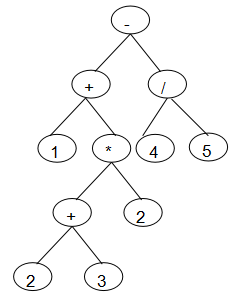
　　2.3.2 设计思路（伪代码或流程图）

 

 　　　　

　　　　

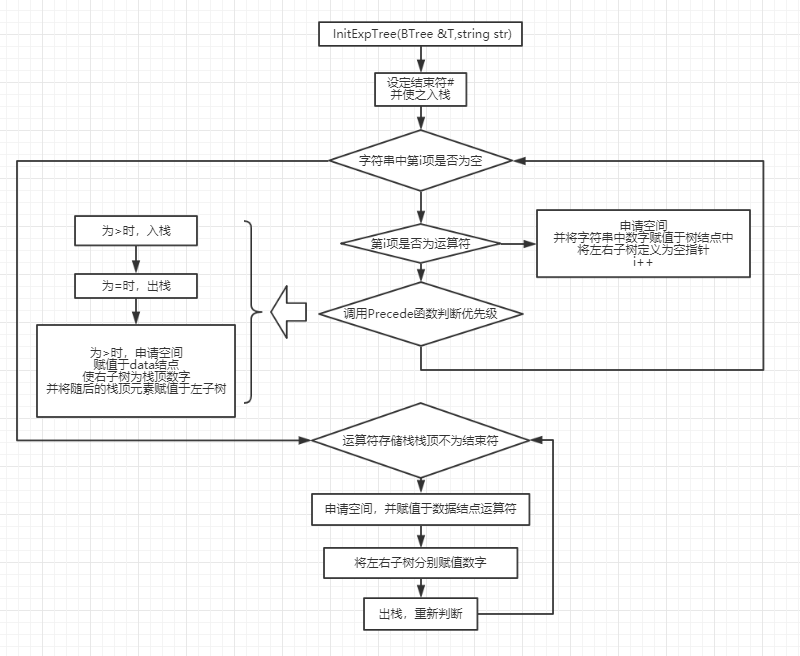
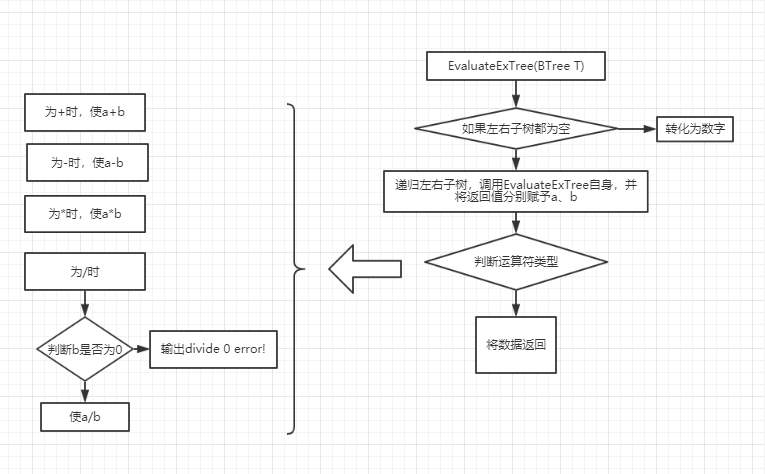
　　　　2.3.3 代码截图

　　　　

　　　　

　　　2.2.4 PTA提交列表说明

　　　　代码不完整，没有考虑到除数为0的时候出现的情况，后补上

---

3.1 PTA排名截图

　　

3.2 我的总分：2.5

本题评分规则：

 （1）2个题目集PTA总分285分：3分（全部题目都做）
 （2）PTA总分在230分--340分：2.5分（必做题全部做完，选做题做部分）
 （3）PTA总分在180--230分：2分（必做题大部分做完）
 （4）PTA总分在130--180分：1.5分
 （5）PTA总分在105分-130分：1分  
 （6）PTA总分在105分以下：0分     

4. 阅读代码

 　　　　

/*
问题：
    Given two non-empty binary trees s and t, check whether tree t has exactly the same structure
    and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all
    of this node's descendants. The tree s could also be considered as a subtree of itself.
    Example 1:
    Given tree s:
     3
    / \
   4   5
  / \
 1   2
    Given tree t:
   4 
  / \
 1   2
    Return true, because t has the same structure and node values with a subtree of s.
    Example 2:
    Given tree s:
     3
    / \
   4   5
  / \
 1   2
    /
   0
    Given tree t:
   4
  / \
 1   2
    Return false.
*/
/*
解答：
    1.方法一直接前序遍历，然后在判断两个树是否相等。
    2.方法二先通过计算树的高度，初步判断树t可能出现在树s的第几层，然后在判断两个树是否相等。
*/
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
/*
class Solution
{
public:
    bool isSametree(TreeNode* p, TreeNode* q)
    {
        if(!p && !q) return true;
        if(!p || !q || p->val!=q->val) return false;
        return isSametree(p->left, q->left) && isSametree(p->right, q->right);
    }
    bool isSubtree(TreeNode* s, TreeNode* t)
    {
        if(!s && !t) return true;
        if(!s || !t) return false;
        if(s->val == t->val)
            if(isSametree(s, t))
                return true;
        if(isSubtree(s->left, t))
            return true;
        if(isSubtree(s->right, t))
            return true;
        return false;
    }
};
*/
class Solution {
    vector<TreeNode*> nodes;

public:
    bool isSubtree(TreeNode* s, TreeNode* t) {
        if (!s && !t) return true;
        if (!s || !t) return false;

        getDepth(s, getDepth(t, -1));

        for (TreeNode* n: nodes)
            if (identical(n, t))
                return true;

        return false;
    }

    int getDepth(TreeNode* r, int d) {
        if (!r)
            return -1;

        int depth = max(getDepth(r->left, d), getDepth(r->right, d)) + 1;

        // Check if depth equals required value
        // Require depth is -1 for tree t (only return the depth, no push)
        if (depth == d)
            nodes.push_back(r);

        return depth;
    }

    bool identical(TreeNode* a, TreeNode* b) {
        if (!a && !b) return true;
        if (!a || !b || a->val != b->val) return false;

        return identical(a->left, b->left) && identical(a->right, b->right);
    }
};

　　　　给出树t以及树s，判断s是否为t的子树，若是返回真，若不是返回假。

　　　　个人较为喜欢第二种方法，通过计算树的高度，初步判断树t可能出现在树s的第几层，然后在判断两个树是否相等。这样能够使处理体量更为巨大的树时节省计算量。

　　　　地址：https://gitee.com/specialsoldier/codes/l05jietvp9zuq1mfars4360

---

5. 代码Git提交记录截图