OI的Trick整理(已经整理40个)
笔者整理本文,主要整理一些有可能大家不会专门学的Trick,也包含一些冷门算法,这里给出了很多题目
欢迎大家补充qwq
1.在长为n的序列里枚举子集,再在子集里枚举子集
时间复杂度\(3^n\),因为每种三进制对应一种情况
快速枚举子集方式(假设是状压,每个输出对应一个子集中的子集):
for (int s=0;s<(1<<n);s++){
for (int i=s;i;i=(s&(i-1))){
cout<<i<<endl;
}
cout<<0<<endl;//空集合前面没有枚举到
}
2.bitset优化矩乘
如果我们重定义矩阵运算,定义成异或和,那么矩阵 \(a\) 和矩阵 \(b\) 间的运算是这样的:
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
for (int k=1;k<=n;k++)
ans[i][j]=(ass[i][j]^(a[i][k]^b[k][j]));
如果矩阵中所有的数都是 \(0\) 或 \(1\) ,那么可以用bitset优化:
bitset<N> ans[N],a[N],b[N];
int x;
for (int i=1;i<=k;i++)
for (int j=i+1;j<=k;j++)
x=b[i][j],b[i][j]=b[j][i],b[j][i]=x;//bitset好像用不了swap
for (int i=1;i<=k;i++){
for (int j=1;j<=k;j++){
ans[i][j]=(a[i]&b[j]).count() & 1;
应该很好理解吧?
3.严格次小生成树
应该有人没学过?
首先建最小生成树,预处理倍增求 \(lca\) ,然后枚举每一条不在最小生成树上的边,设这条边将 \(u,v\) 联通,边权为 \(w\)
那么这条边如果加入了最小生成树,那么就会形成从 \(u\) 开始,到 \(lca(u,v)\) 再到 \(v\) ,再到 \(u\) 的环
那么在环里随便断开一边,就又会变成一个树
删掉一条不等于 \(w\) 的环上边权最大的边,就可以得到相对最小的生成树了
求不等于 \(w\) 的环上边权最大的边可以在预处理倍增时维护最大值和次大值实现
洛谷板子题链接
4.\(unordered\)_\(set\)理论时间复杂度吊打\(set\)
如果你想查询一个数是否存在,可以手搓哈希表(码量比较多)
当然你如果不介意时间复杂度多一个 \(log\) 你可以用 \(set\)
你可以考虑用 \(unordered\)\(set\) ,这个可爱的 \(STL\) 是哈希表,用法与 \(set\) 一样,理论时间复杂度均摊 \(O(1)\)
但是出题人很有可能卡你 \(unordered\)\(set\) ,所以最好手搓哈希表或加 \(log\) 能过的话用 \(set\)
你用 \(unordered\)_\(set\) 被毒瘤出题人卡飞别找我
同理,把 \(map\) 改为 \(unordered\)_\(map\) 也能获得 \(O(1)\) 的理论时间复杂度,但是可能会被卡
5.树上一类问题看似\(O(n^3)\)实际\(O(n^2)\)
如果你要树上\(dp\),而且形式是这个样子的:
void dfs(int d,int fa){
siz[d]=1;
for (int k=qi[d];k;k=e[k].nx){
int v=e[k].to;
if (v==fa) continue;
dfs(v,d);
for (int i=1;i<=siz[d];i++){
for (int j=1;j<=siz[v];j++){
一些转移
}
}
siz[d]+=siz[v];
}
}
时间复杂度是 \(O(n^2)\) 的,因为可以理解成枚举任意两点,在它俩的 \(lca\) 处转移
那么!
如果形式是这个样子的:
void dfs(int d,int fa){
siz[d]=1;
for (int k=qi[d];k;k=e[k].nx){
int v=e[k].to;
if (v==fa) continue;
dfs(v,d);
for (int i=1;i<=min(l,siz[d]);i++){
for (int j=1;j<=min(l,siz[v]);j++){
一些转移
}
}
siz[d]+=siz[v];
}
}
(这里的 \(l\) 是限制条件)
时间复杂度是 \(O(nl)\) 的,相当于在有 \(n\) 个点树中长度不超过 \(l\) 的简单路径的数目
6.如果数据范围为乘积的形式
如果数据范围为 \(n*m<=10^5\) ,而且你有两个算法,一个 \(O(n^2m)\) 一个 \(O(nm^2)\)
那么你可以判断 \(n\) 大还是 \(m\) 大,从而采取最优的方法
最大时间复杂度是 \(n=m=\sqrt{10^5}\) 的时候, \(O(10^5\sqrt{10^5})\)
洛谷有一道题就是这样
最水的一个Trick
7.欧拉路径的边定向问题
欧拉路径是OI中不常见的问题
我们可以利用欧拉路径的性质,给边定向或染色,以达到题目的要求
详细教程在这里
8.斐波那契数列的前缀和
你肯定知道斐波那契数列是什么
设 \(f(i)\) 为斐波那契数列的第 \(i\) 项
斐波那契数列的通项公式:
\({f}(n)=\frac{\varphi^{n}-(1-\varphi)^{n}}{\sqrt{5}}\)
其中\(\varphi=\frac{1+\sqrt{5}}{2}\)
(没什么用的样子)
观察:
\(f(1)=f(3)-f(2)\)
\(f(1)+f(2)=f(3)-f(2)+f(4)-f(3)=f(4)-f(2)\)
\(f(1)+f(2)+f(3)=f(3)-f(2)+f(4)-f(3)+f(5)-f(4)=f(5)-f(2)\)
可知\(\sum_{i=1}^{n} f(i)=f(n+2)-f(2)\)
这样的话我们就可以愉快地求斐波那契数列的前缀和了!
9.求一段数的异或值
有个规律
假设我们要求\(1异或2异或3异或4......异或x\)
以下代码可以轻松办到
int compute_xor_prefix(int x) {
if (x % 4 == 0)
return x;
else if (x % 4 == 1)
return 1;
else if (x % 4 == 2)
return x + 1;
else
return 0;
}
10.更快地求gcd的方法
你肯定会碾转相除法
如果你的瓶颈在 \(gcd\) ,担心时间过不了,不妨试试 \(stein\) 算法
\(Stein\) 算法的关键就在于除2操作,具体表现如下:
\(a偶b偶:gcd(a, b) = 2 * gcd(a/2, b/2)\)
\(a偶b奇:gcd(a, b) = gcd(a/2, b)\)
\(a奇b偶:gcd(a, b) = gcd(a, b/2)\)
\(a奇b奇:gcd(a, b) = gcd(|a-b|, min\){\(a, b\)}\()\)
我们可以用位运算优化
见代码
long long gcd(long long x,long long y){
if(!x) return y;
if(!y) return x;
long long t=__builtin_ctzll(x|y);
x>>=__builtin_ctzll(x);
//__builtin_ctzll是GCC内置函数,计算一个数的二进制表示末尾0的个数,跑得很快
while(y){
y>>=__builtin_ctzll(y);
if(x>y) swap(x,y);
y-=x;
}
return x<<t;
}
11.高维前缀和
有时我们要开一个这样的数组\(f[a_1][a_2]…[a_n]\)
如果你要求前缀和
如果你写 \(n\) 个循环,你会累死
你可以把每项压缩成一个数字(细节比较多)
然后钦定当前要转移第 \(i\) 维
拿 \(dfs\) 搜剩下的维度,就可转移
这个 \(Trick\) 经常出现在给一个数的约数转移的时候
洛谷上应用了这个思路的题
12.\(KMP\)用来找一串字符最小的循环节
预先处理字符串 \(s\) 的 \(Next\) 数组,那么一个长度为 \(j\) 的前缀的最小循环节长度为:
if(i%(i-Next[i])==0){
cout<<i-Next[i];
}
else cout<<i;
13.快速找一个点在树内与任意一点最远距离
首先求出树的直径,任意一点在树内与任意一点最远距离就是 \(max(它到树的直径一端点距离,它到树的直径另一端点距离)\)
树剖或倍增求距离(有时需要 \(splay\))
同理,如果在两棵树间连边,新的树的直径就是他俩原来的直径的端点两两组合的最长的那个
14.如果输入是整数,输出也是整数,中间运算时不是整数还要取模
假设你中间运算时的数有可能是 \(a+b\sqrt{5}\) 的形式,不妨仿照 \(FFT\) 的复数类一样开一个类,支持加减乘取模操作
如果要除以一个形如 \(a+b\sqrt{5}\) 的数,显然带着根号求不了逆元
可以变成乘上 \(\frac{(a-\sqrt{b})}{(a+\sqrt{b})(a-\sqrt{b})}\) ,显然此时 \((a+\sqrt{b})(a-\sqrt{b})\) 是整数,就可以愉快地求它的逆元了
15.如果在一个矩阵中不能遍历全部的格点
给你一个 \(n*m\) 的矩阵,其中 \(1<=n,m<=10^5\) ,然后给出 \(k\) 个关键点的坐标 \(1<=k<=10^5\) ,求一些东西(比如如果去掉这些点原图还连不连通)
我就不在这里说方法了,大家自己去看洛谷题解
洛谷上的题
然后ABC413G题可以应用这个方法,于是我把这题场切了
16.最短路图与次短路图
在图中,要判断一个点是否在从 \(s\) 到 \(t\) 的最短路上,只要判断这个点到 \(s\) 最短长度加到 \(t\) 的最短长度,如果等于最短路的长度,那么这个点就在最短路上了。保留原图的在最短路上的点间的边,就成了最短路图,而且这个图是 \(TAG\) ,除非有零环
那么判断次短路时,视情况而定(比如能不能走重边,有无边权),能不能用这种思路建出次短路图
有些题需要建出最短路图或次短路图然后跑 \(dp\) 或 \(Tarjan\)
我记得我见过这样的题,但找不着链接,欢迎大家补充
17.四边形不等式常加整体二分
当你知道交叉小于包含时,你知道决策点单调递增
可以整体二分,就是写个函数类似线段树建树,传入参数表明第几到第几项的决策点是第几到第几个,然后 \(mid\) 是第几项的 \(mid\)
例题:Loj 6039 珠宝(自己去百度搜)
18.线段树优化建图
很经典了,学习链接
19.比较两个带除法的式子是否相等
假设你要比较 \(\frac{a}{b}\) 是否等于 \(\frac{c}{d}\) ,直接算有可能精度起飞
你可以两边同乘 \(bd\) ,然后比较 \(ad\) 和 \(bc\) 就行了
20.给两个相同长度的数组比字典序
用 \(vector\) 更方便,支持直接比较
最最水的一个Trick
21.和哈希
有时你要快速判断一个东西是否和另一个东西等价,这个东西有一部分可以改变顺序,有一部分不行
你需要设计个符合“等价”条件的哈希,然后判断哈希值是否相等
这些语言可能难理解,见例题
[CSP-S 2022] 星战
[NOI2024] 集合
欢迎补充
22.DFS抽象优化,dfs时顺便解一个方程
如果你要搜一个合法序列,正常搜会T,再进行一点优化就能过
你可以设这个序列的某一项为 \(x\) ,然后继续搜,每次贡献是 \(x\) 解的个数
此题[NOI2024] 分数
然后如果你搜到剩最后两项,有可能可以列一个方程,转换为枚举另一个东西,减少枚举量
此题埃及分数埃及人做梦也想不到,他们发明的这个东西让后人绞尽脑汁
23.带权并查集
假设给出一些点,每次连一条带权有向边,保证永远是内向树或森林,有询问,询问一个点到它的根的路径长度
使用带权并查集,想知道更多细节的自行百度,例题我找不到,欢迎补充
24.树上联通块数量
求树上不同联通块数量
你 \(dp\) 自然可以,这里有另一种方法
可以枚举每个点计算贡献,但是会重
考虑树上联通块的特征是点数-边数=1
于是可以枚举每个点计算贡献减去枚举每个边的贡献
25.\(Min-Max\) 对抗搜索
俩人玩一个游戏,甲的目的是尽量让一个数字变大,乙反之
可以搜索,如果这次是甲的回合,就选后续状态对他最优的,反之亦然
具体细节自行百度,因为我没有例题,讲不明白
26.长链剖分
27.离线求一堆逆元
假设你要求一堆数的逆元,你可以求出前缀积后缀积和总积的逆元,然后就可以 \(O(n)\) 求了
28.全局与单点操作
假设维护序列,只有单点修改、全局加、乘
可以做到 \(O(n)\) (可能需要离线处理逆元)
板子链接
29.\(dsu on tree\) 和线段树合并
很多题目用 \(dsu on tree\) 时间复杂度双 \(log\) ,用线段树合并单 \(log\) ,但是绝大部分题目两种方法都可以过
30.回退数据结构
有时你在树上要求出f和g函数,求g需要自下而上,求f反之,你求g需要维护一个数据结构,然后求f的时候要用到当前的g的数据结构以及自己祖先的f
你可以记录求g时数据结构修改顺序,然后求f的时候颠倒所有点的儿子,把数据结构回退到那个点即可求了
例题:
P10789 [NOI2024] 登山
[十二省联考 2019] 绝望希望
31.边分治优化建图
只见过一道例题:
AT_abc414_f [ABC414F] Jump Traveling
32.舞蹈链(DLX)
你这辈子可能都用不到的一个搜索方式
板子链接
33.DAG链剖分
34.摩尔投票法
有时候要求区间众数,自然有常规的分块做法
有时众数附加这个条件:超过区间大小一半。这时候可以用摩尔投票法,用线段树和平衡树维护
摩尔投票法的核心思想为对拼消耗,考虑一个序列,我们每次取出两个数,如果相同就放回,不同的话就抵消,把这两个数全都删除,直到序列为空或剩一种数。如果序列空了就说明它没有众数,否则剩下的这种数就可能是这个序列的众数。注意被其他的数绝不可能成为答案,剩下的这个是不是答案还需拿平衡树要检验
例题
[NOI2022] 众数
35.整数到整数映射
假设你要写哈希,有时候可以整数到整数映射
可以把x映射到第x个质数的值
也可以这么样:
const ull mask = std::mt19937_64(time(nullptr))();
ull shift(ull x) {
x ^= mask;
x ^= x << 13;
x ^= x >> 7;
x ^= x << 17;
x ^= mask;
return x;
}
mask防止出题人卡你
36.树上问题的一类均摊
给出一颗类似线段树的树形式,要求出每个点的某个函数才能算出答案,要依次修改每个叶子的函数值,然后其祖先函数值可能会变化
最简单的维护函数值方式就是枚举叶子的所有祖先
可以思考是否具有特殊性质或者构造一个符合这个特殊性质的函数,使得树上每个节点的函数值只会被修改常数次,然后修改叶子后修改的祖先排成一个链
我只见过一个题,但是感觉非常有启发
[CSP-S 2024] 擂台游戏
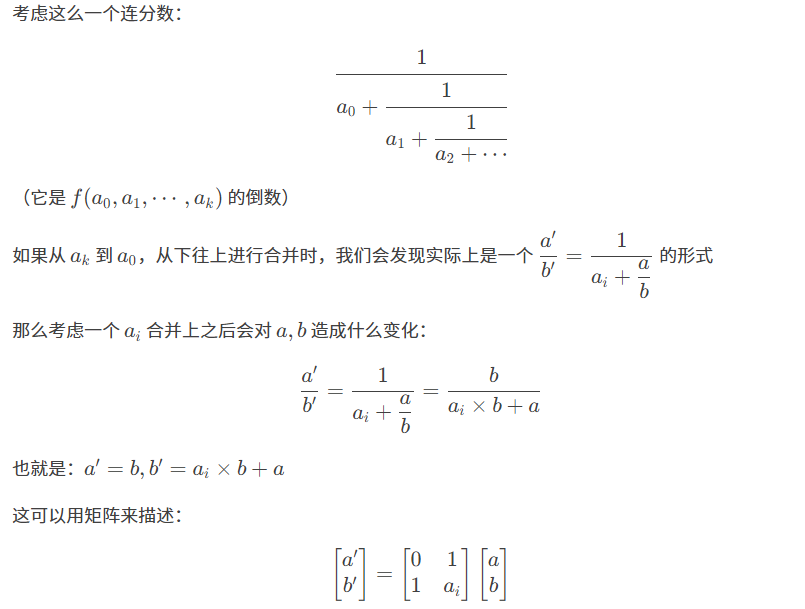
37.矩阵与连分数间关系
38.DAG图的转换
如果有一个只有一个点入度为零的话
如果只考虑连通性以及谁是谁的祖先、后代问题,那么可以拓扑排序再加上一些操作转换成树,这样就能实现更多操作了
有时候一个题需要:
有向图——>DAG——>树
比如这个题:
P7737 [NOI2021] 庆典
39.区间dp的优化
如果转移的时间复杂度是一个常数,那么想求dp[1][n]正常的时间复杂度是平方
有一个优化:记忆化搜索!
可以发现如果是记忆化搜索有一部分区间搜索不到!
而且很有可能搜到的区间并不多,大大优化时间复杂度
40.兔队线段树
指一些pushup操作需要在子树内二分的线段树,总的时间复杂度 \(O(nlog^2n)\) ,计算动态单点修改的序列有多少不同的前缀最大值问题会用到,例题我找不到了





 浙公网安备 33010602011771号
浙公网安备 33010602011771号