抛物线与椭圆

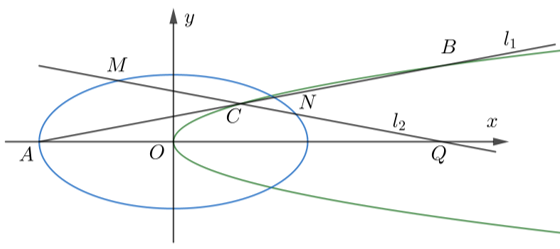
如图，已知椭圆 \(C_1:\dfrac{x^2}{4}+y^2=1\) ，抛物线 \(C_2:y^2=2px(p>0)\) ，过椭圆 \(C_1\) 的左顶点 \(A\) 的直线 \(l_1\) 交抛物线 \(C_2\) 于 \(B,C\) 两点，且 \(\overrightarrow{AC}=\overrightarrow{CB}\) .

(1) 求证：点 \(C\) 在定直线上；

(2) 若直线 \(l_2\) 过点 \(C\) ，交椭圆 \(C_1\) 于 \(M,N\) 两点，交 \(x\) 轴于点 \(Q\) ，且 \(|CA|=|CQ|\) ，当 \(\triangle BMN\) 的面积最大时，求抛物线 \(C_2\) 的方程。

解析：

(1) 求得 \(A(-2,0)\) ，设直线 \(l_1:x=my-2\) ，\(C(x_1,y_1),B(x_2,y_2)\) ，联立

\[\begin{cases}x=my-2\\y^2=2px\end{cases}\Longrightarrow y^2-2pmy+4p=0 \]

则

\[y_1+y_2=2pm\;,\;y_1y_2=4p \]

而

\[y_1^2y_2^2=4p^2x_1x_2\Longrightarrow x_1x_2=\dfrac{y_1^2y_2^2}{4p^2}=4 \]

又 \(\overrightarrow{AC}=(x_1+2,y_1),\overrightarrow{CB}=(x_2-x_1,y_2-y_1)\) ，由 \(\overrightarrow{AC}=\overrightarrow{CB}\) 得

\[\begin{cases}x_1+2=x_2-x_1\\y_1=y_2-y_1\end{cases} \]

所以 \(x_2=2x_1+2\) ，又 \(x_1x_2=4\) ，解得 \(x_1=1\) 或 \(x_1=-2\) (舍) . 所以点 \(C\Big(1,\dfrac{3}{m}\Big)\) ，易得点 \(C\) 在定直线 \(x=1\) 上，得证。

(2) 由 (1) 得 \(x_2=4\) ，则 \(B(4,\dfrac6m)\). 又 \(k_{CQ}=-k_{AC}=-\dfrac{1}{m}\) ，则 \(l_2:x+my-4=0\) ，设 \(M(x_3,y_3),N(x_4,y_4)\) ，联立

\[\begin{cases}x+my-4=0\\x^2+4y^2=4\end{cases}\Longrightarrow (m^2+4)y^2-8my+12=0 \]

得 \(y_3+y_4=\dfrac{8m}{m^2+4},y_3y_4=\dfrac{12}{m^2+4}\) ，所以

\[\begin{align}|MN|&=\sqrt{1+\dfrac{1}{k^2}}\cdot\sqrt{(y_3+y_4)^2-4y_3y_4}\\&=\sqrt{1+m^2}\cdot\sqrt{\dfrac{64m^2}{(m^2+4)^2}-\dfrac{48}{m^2+4}}\\&=\sqrt{1+m^2}\cdot\sqrt{\dfrac{16(m^2-12)}{(m^2+4)^2}}\end{align} \]

而 \(B\) 到直线 \(l_2\) 的距离 \(d=\dfrac{6}{\sqrt{1+m^2}}\) ，故

\[\begin{align}S_{\triangle BMN}&=\dfrac12\cdot\sqrt{1+m^2}\cdot\sqrt{\dfrac{16(m^2-12)}{(m^2+4)^2}}\cdot\dfrac{6}{\sqrt{1+m^2}}=12\sqrt{\dfrac{m^2-12}{(m^2+4)^2}}\end{align} \]

令 \(m^2-12=t>0\) ，则 \(m^2=t+12\) ，则

\[S_{\triangle BMN}=12\sqrt{\dfrac{t}{t^2+32t+256}}=12\sqrt{\dfrac{1}{t+\dfrac{256}{t}+32}}\leqslant12\sqrt{\dfrac{1}{2\sqrt{256}+32}}=\dfrac32 \]

当且仅当 \(t=\dfrac{256}{t}\) ，即 \(t=16\) ，\(m=\sqrt{28}\) 时，等号成立，\(\triangle BMN\) 面积取最大值，此时 \(C\Big(1,\pm\dfrac{3}{\sqrt{28}}\Big)\) ，代入抛物线方程得 \(C_2:y^2=\dfrac{9}{28}x\).