暴力计算离心率

已知 \(F\) 为双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>b>0)\) 的右焦点，过点 \(F\) 的直线交两渐近线于 \(A,B\) 两点，如 \(\angle OAB=120^{\circ}\) ，\(\triangle OAB\) 的内切圆的半径 \(r=\dfrac{\sqrt3a-b}{5}\) ，则双曲线的离心率为 \(\underline{\qquad\qquad}.\)

解法一：

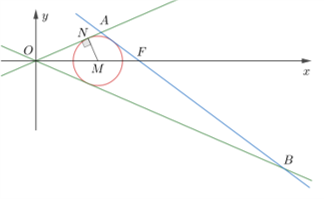
如图，易知 \(\triangle OAB\) 的内心在 \(x\) 轴上，设为 \(M(m,0),(m>0)\) ，作 \(MN\perp OA\) 垂足为 \(N\). 又直线 \(OA:bx-ay=0\) ，依题意得

\[MN=\dfrac{|mb|}{\sqrt{a^2+b^2}}=\dfrac{\sqrt3a-b}{5}\Longrightarrow m=\dfrac{(\sqrt3a-b)c}{5b} \]

设渐近线 \(OA\) 的倾斜角为 \(\theta\) ，则

\[k_{AB}=\tan(\theta+\dfrac{2\pi}{3})=\dfrac{\tan\theta+\tan\dfrac{2\pi}{3}}{1-\tan\theta\tan\dfrac{2\pi}{3}}=\dfrac{b-\sqrt3a}{a+\sqrt3b} \]

则直线 \(AB\) 的方程为

\[\dfrac{b-\sqrt3a}{a+\sqrt3b}(x-c)-y=0 \]

又点 \(M\) 到直线 \(AB\) 的距离

\[d=\dfrac{\Big|\dfrac{b-\sqrt3a}{a+\sqrt3b}\cdot\Big( \dfrac{(\sqrt3a-b)c}{5b}- c\Big)\Big|}{\sqrt{\Big(\dfrac{b-\sqrt3a}{a+\sqrt3b}\Big)^2+1}}=\dfrac{\sqrt3a-b}{5} \]

易知 \(b-\sqrt3a<0\) ，又内心 \(M\) 在焦点 \(F\) 的左边，所以 \(\dfrac{(\sqrt3a-b)c}{5b}- c<0\)，故上式化简得

\[\sqrt3a=4b\;\Longrightarrow\;\dfrac{b}{a}=\dfrac{\sqrt3}{4} \]

所以双曲线的离心率 \(e=\sqrt{1+\Big(\dfrac{\sqrt3}{4}\Big)^2}=\dfrac{\sqrt{19}}{4}.\)

解法二：

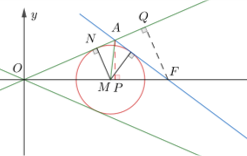
如图，由点 \(F\) 向 \(OA\) 作垂线，垂足为 \(Q\) ，则 \(QF=\dfrac{|bc|}{\sqrt{a^2+b^2}}=b\) ，又 \(\angle QAF=60^{\circ}\) ，所以 \(AF=\dfrac{QF}{\sin60^{\circ}}=\dfrac{2\sqrt3}{3}b\) ，在 \(\triangle OAF\) 中，由余弦定理得

\[c^2=OA^2+\Big(\dfrac{2\sqrt3}{3}b\Big)^2-2\cdot OA\cdot\dfrac{2\sqrt3}{3}b\cdot\cos120^{\circ} \]

解得 \(OA=\dfrac{3a-\sqrt3b}{3}\) . 作 \(AP\perp OF\) ，垂足为 \(P\) ，设 \(OP=ax,AP=bx\) ，则

\[(ax)^2+(bx)^2=OA^2 \]

解得 \(AP=\dfrac{b}{c}\cdot OA=\dfrac{(3a-\sqrt3b)b}{3c}\) . 故由 \(S_{\triangle OAF}=S_{\triangle OAM}+S_{\triangle AMF}\) 得

\[\dfrac12\cdot c\cdot\dfrac{(3a-\sqrt3b)b}{3c}=\dfrac12\cdot\dfrac{3a-\sqrt3b}{3}\cdot\dfrac{\sqrt3a-b}{5}+\dfrac12\cdot\dfrac{2\sqrt3}{3}b\cdot\dfrac{\sqrt3a-b}{5} \]

化简得

\[\sqrt3a=4b\;\Longrightarrow\;\dfrac{b}{a}=\dfrac{\sqrt3}{4} \]

所以双曲线的离心率 \(e=\sqrt{1+\Big(\dfrac{\sqrt3}{4}\Big)^2}=\dfrac{\sqrt{19}}{4}.\)