角平分线

若 \(AB=4,\overrightarrow{AC}=3\overrightarrow{CB}\) ，平面内一点 \(P\) ，满足 \(\dfrac{\overrightarrow{PA}\cdot\overrightarrow{PC}}{|\overrightarrow{PA}|}=\dfrac{\overrightarrow{PB}\cdot\overrightarrow{PC}}{|\overrightarrow{PB}|}\) ，\(\sin\angle PAB\) 的最大值是 \(\underline{\qquad\qquad}\) .

【解析】

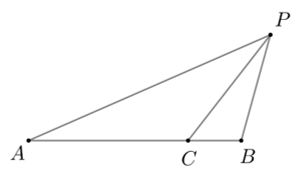
如图，依题意有

\[\dfrac{|\overrightarrow{PA}||\overrightarrow{PC}|\cos\angle APC}{|\overrightarrow{PA}|}=\dfrac{|\overrightarrow{PB}||\overrightarrow{PC}|\cos\angle BPC}{|\overrightarrow{PB}|}\Longrightarrow \angle APC=\angle BPC \]

因为 \(\overrightarrow{AC}=3\overrightarrow{CB}\) ，所以 \(|AC|=3|CB|\) ，根据角平分线定理得

\[\dfrac{|AP|}{|BP|}=\dfrac{|AC|}{|CB|}=3 \]

设 \(|BP|=a\) ，则 \(|AP|=3a\) ，则

\[\cos\angle PAB=\dfrac{9a^2+16-a^2}{2\cdot3a\cdot4}=\dfrac{a}{3}+\dfrac{2}{3a}\geqslant2\sqrt{\dfrac{a}{3}\cdot\dfrac{2}{3a}}=\dfrac{2\sqrt2}{3} \]

当且仅当 \(\dfrac{a}3=\dfrac{2}{3a}\) ，即 \(a=\sqrt2\) 时，\(\cos\angle PAB\) 最小值为 \(\dfrac{2\sqrt2}{3}\) ，易知 \(\angle PAB\in\Big(0,\dfrac{\pi}{2}\Big)\) ，故此时 \(\sin \angle PAB\) 取最大值 \(\dfrac13\) .