可持久化数据结构

可持久化数据结构

首先需要知道，何谓可持久化？具体而言，就是对每次操作保留一个历史版本，同时可以基于其中一个历史版本进行操作，且复杂度在可接受范围内。

显然不能每次都拷贝一遍，但是利用一些性质，一些常见的数据结构都是在同样的复杂度下做到可持久化的。

可持久化线段树（主席树）

其实主席树不完全等于可持久化线段树，而是可持久化权值线段树。不过现在似乎不太区分这个，索性都这么叫了。

基本思想

不能每次都开一棵线段树，考虑到线段树每次修改的一个重要性质：每次修改只会修改 \(\boldsymbol{O(\log n)}\) 个节点。

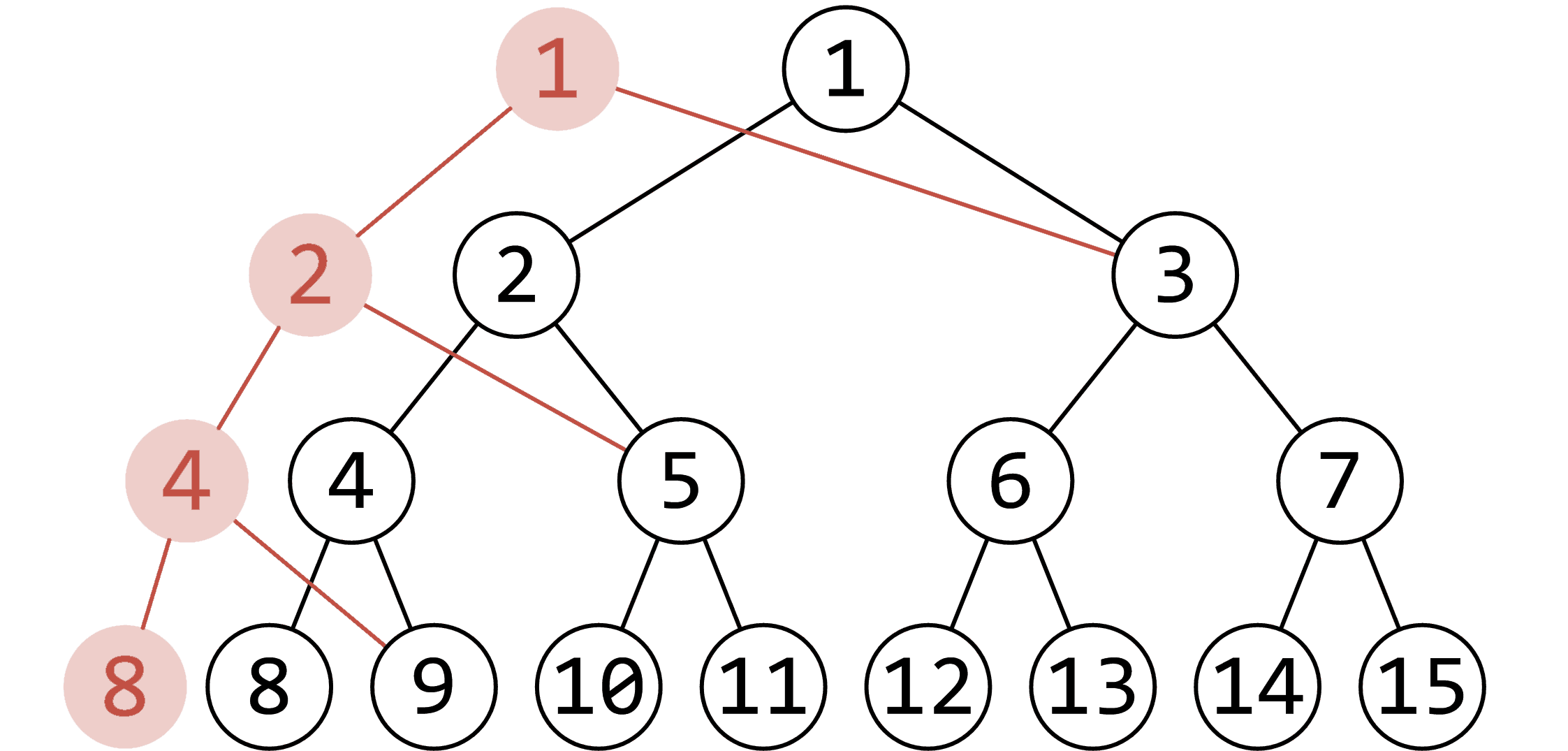
（图源 OI Wiki）

所以简单地，采用动态开点的方式储存儿子，每次修改的时候把需要修改的节点新开一个，然后储存每次修改后的根节点就能实现可持久化了。这样的时间和空间复杂度都是 \(O(n\log n)\) 的。

实际上对于 \(O(n\log n)\) 这个空间上限不一定完全保证。

并且主席树的题目空间限制都比较松，建议尽量开大一点，不是坏事。

注意可持久化线段树不能按照下放懒标记的方式进行区间修改，因为有共用的节点。所以在可持久化线段树上进行区间修改需要采取标记永久化的方式。具体实现如下：

void mdf(int l,int r,ll k,int s,int t,int q,int&p){
    st[p=++tot]=st[q];
    st[p].c+=(min(t,r)-max(s,l)+1)*k;
    if(l<=s&&t<=r) return st[p].lazy+=k,void();
    int mid=(s+t)>>1;
    if(l<=mid) mdf(l,r,k,s,mid,lq,lp);
    if(mid<r) mdf(l,r,k,mid+1,t,rq,rp);
}
ll sum(int l,int r,int s,int t,ll tag,int p){
    if(l<=s&&t<=r) return st[p].c+(t-s+1)*tag;
    int mid=(s+t)>>1;
    ll res=0;
    if(l<=mid) res+=sum(l,r,s,mid,tag+st[p].lazy,lp);
    if(mid<r) res+=sum(l,r,mid+1,t,tag+st[p].lazy,rp);
    return res;
}

简单来说就是修改途中一路更改受影响的点，然后查询途中累加一路的标记。

应用

静态区间 k 小值

典型例题：P3834 【模板】可持久化线段树 2。

这是主席树的常见应用。当然整体二分也可以做，但如果强制在线就似了。下面介绍用主席树维护的方法。

首先考虑如何求出全局 \(k\) 小值。显然建出权值线段树然后线段树二分即可。

然后考虑如何求出 \([1,r]\) 的 \(k\) 小值。学会了主席树，我们就知道建出主席树后在 \(r\) 的根节点版本上进行线段树二分即可。

最后考虑如何求出 \([l,r]\) 的 \(k\) 小值。这里运用了前缀和的思想，我们发现区间 \([l,r]\) 的统计信息只需用 \([1,r]\) 减去 \([1,l-1]\) 即可。于是问题得解。

constexpr int MAXN=2e5+5;
int n,m,a[MAXN],b[MAXN],rt[MAXN],tot;
struct{
	#define lp st[p].lc
	#define rp st[p].rc
	#define lq st[q].lc
	#define rq st[q].rc
	struct SegTree{
		int lc,rc,c;
	}st[MAXN<<5];
	void build(int s,int t,int&p){
		p=++tot;
		if(s==t) return;
		int mid=(s+t)>>1;
		build(s,mid,lp),build(mid+1,t,rp);
	}
	void chg(int x,int s,int t,int q,int&p){
		st[p=++tot]=st[q];
		st[p].c++;
		if(s==t) return;
		int mid=(s+t)>>1;
		if(x<=mid) chg(x,s,mid,lq,lp);
		else chg(x,mid+1,t,rq,rp);
	}
	int ask(int l,int r,int k,int q,int p){
		if(l==r) return l;
		int mid=(l+r)>>1,res=st[lp].c-st[lq].c;
		if(res>=k) return ask(l,mid,k,lq,lp);
		else return ask(mid+1,r,k-res,rq,rp);
	}
}T;

int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) T.chg(read(),0,1e9,rt[i-1],rt[i]);
	while(m--){
		int l=read(),r=read(),k=read();
		write(T.ask(0,1e9,k,rt[l-1],rt[r]));
	}
	return fw,0;
}

动态区间 k 小值

典型例题：P2617 Dynamic Rankings。

从静态变为动态，如果暴力的话，单点修改位置 \(x\) 导致我们需要重构从 \(x\) 到 \(n\) 的主席树，显然超时。

但是由上可知，主席树本质上维护的是前缀和信息，而上文的暴力算法本质上是暴力修改前缀和数组，然后利用前缀和数组求出我们想要的答案，所以这个问题的本质就是单点修改、区间查询。

于是自然想到可以把树状数组套在这个上面优化。具体地，将树状数组的每一个点看作一个主席树，修改的时候对受影响的节点正常修改即可，但查询的时候需要先跑出所有受影响的节点，然后对应地一起作差才是正确的答案。

本质上这仍然是一种树套树解法，即树状数组套权值线段树，但比一般的树套树（线段树套平衡树）的复杂度低一个 \(\log\)，是 \(O(n\log^2n)\) 的。

constexpr int MAXN=1e5+5;
int t,n,m,a[MAXN],rt[MAXN];
vector<int>P,Q;
struct{
	#define lp st[p].lc
	#define rp st[p].rc
	struct SegTree{
		int lc,rc,c;
	}st[MAXN*300];
	int tot;
	void chg(int x,int k,int s,int t,int&p){
		if(!p) p=++tot;
		if(s==t) return st[p].c+=k,void();
		int mid=(s+t)>>1;
		if(x<=mid) chg(x,k,s,mid,lp);
		else chg(x,k,mid+1,t,rp);
		st[p].c=st[lp].c+st[rp].c;
	}
	int sum(int l,int r,int k){
		if(l==r) return l;
		int mid=(l+r)>>1,res=0;
		for(auto p:P) res+=st[lp].c;
		for(auto p:Q) res-=st[lp].c;
		if(res>=k){
			for(auto&p:P) p=lp;
			for(auto&p:Q) p=lp;
			return sum(l,mid,k);
		}else{
			for(auto&p:P) p=rp;
			for(auto&p:Q) p=rp;
			return sum(mid+1,r,k-res);
		}
	}
}T;
struct{
	#define lowbit(x) (x&-x)
	void add(int x,int k){
		for(int i=x;i<=n;i+=lowbit(i)) T.chg(a[x],k,0,1e9,rt[i]);
	}
	int ask(int l,int r,int k){
		P.clear(),Q.clear();
		for(int i=r;i;i-=lowbit(i)) P.emplace_back(rt[i]);
		for(int i=l-1;i;i-=lowbit(i)) Q.emplace_back(rt[i]);
		return T.sum(0,1e9,k);
	}
}B;

int main(){
	cin.tie(nullptr)->sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i],B.add(i,1);
	while(m--){
		char op;
		int x,y;
		cin>>op>>x>>y;
		if(op=='Q'){
			int k;
			cin>>k;
			cout<<B.ask(x,y,k)<<'\n';
		}else{
			B.add(x,-1);
			a[x]=y;
			B.add(x,1);
		}
	}
	return 0;
}

区间数颜色

典型例题：P1972 [SDOI2009] HH的项链。

莫队可以离线 \(O(n\sqrt n)\) 做，树状数组可以离线 \(O(n\log n)\) 做，而主席树是在线 \(O(n\log n)\) 做的。

发现对于一个区间的某个点如果有贡献，当且仅当它在这个区间里首次出现，也就是它上次出现的位置在 \([0,l-1]\) 这个区间。所以用主席树解决的方法就是，记录每个数上次出现的位置，主席树中记录每个位置成为 “某个数上次出现的位置” 的次数，然后对于询问区间 \([l,r]\) 只需统计第 \(r\) 棵树和第 \(l-1\) 棵树在 \([0,l-1]\) 范围内权值的差就是答案。

constexpr int MAXN=1e6+5;
int n,m,lst[MAXN],rt[MAXN];
struct{
	#define lp st[p].lc
	#define rp st[p].rc
	#define lq st[q].lc
	#define rq st[q].rc
	struct SegTree{
		int lc,rc,c;
	}st[MAXN<<5];
	int tot;
	void chg(int x,int s,int t,int q,int&p){
		st[p=++tot]=st[q];
		st[p].c++;
		if(s==t) return;
		int mid=(s+t)>>1;
		if(x<=mid) chg(x,s,mid,lq,lp);
		else chg(x,mid+1,t,rq,rp);
	}
	int ask(int l,int r,int s,int t,int q,int p){
		if(l<=s&&t<=r) return st[p].c-st[q].c;
		int mid=(s+t)>>1,res=0;
		if(l<=mid) res+=ask(l,r,s,mid,lq,lp);
		if(mid<r) res+=ask(l,r,mid+1,t,rq,rp);
		return res;
	}
}T;

int main(){
	n=read();
	for(int i=1,x;i<=n;i++){
		x=read();
		T.chg(lst[x],0,n,rt[i-1],rt[i]);
		lst[x]=i;
	}
    m=read();
	while(m--){
		int u=read(),v=read();
		write(T.ask(0,u-1,0,n,rt[u-1],rt[v]));
	}
	return fw,0;
}

其他例题

P2633 Count on a tree

树上主席树的板子题。我们只需先遍历一遍整棵树，对每个节点开一棵继承自其父亲的主席树储存其权值。最后统计 \([u,v]\) 路径的答案时统计 \(w(u)+w(v)-w(l)-w(\text{fa}(l))\) 即可，其中 \(l=\operatorname{LCA}(u,v)\)。复杂度 \(O(n\log n)\)。

P3302 [SDOI2013] 森林

与上一个题相比增加了合并操作。不妨启发式合并，每次把小的连通块合并到大的上面去，然后暴力重构小的连通块上所有点的主席树和 LCA。这样合并复杂度是 \(O(\log n)\) 的，乘上主席树的 \(O(n\log n)\)，总复杂度 \(O(n\log^2n)\)。

注意因为我们要重构 LCA，显然不能树剖，只能倍增。

P3722 [AH2017/HNOI2017] 影魔

找出这个贡献的本质是某个区间最大值 \(c\) 做出的贡献，先预处理每个点能产生贡献的区间，然后枚举这个区间最大值的位置，分类讨论提供贡献的种类并分别对应出一种在线段树上的操作。发现这种贡献可以被前缀和，所以用主席树维护。

P2839 [国家集训队] middle

对于中位数的维护，需要想到二分答案。二分这个中位数，把小于它的所有数权值记为 \(1\)，大于等于它的所有数权值记为 \(-1\)，于是对答案的判定可以转化成一段区间的求和问题。既然我们要让这个中位数尽量大，也就是要使得这个区间的权值和尽量小。于是对于一组询问 \(a,b,c,d\)，最后选出的 \([l,r]\) 实际上是从区间 \([a,d]\) 中减去 \([a,b-1]\) 的最大前缀和 \([c+1,d]\) 的最大后缀得到的，这个显然用线段树可以维护。

但是我们不能每次都暴力建树。发现如果对每个权值从大到小建树，把 \(1\) 改为 \(-1\) 的总数只有 \(n\)，所以不妨用主席树维护每个权值的线段树，然后对于每次二分到的中位数，在它所对应的线段树上执行上述询问即可。

可持久化并查集

实际上就是用可持久化线段树实现的。

考虑要记录版本就需要用到可持久化数组，也就是需要把 \(\text{fa}\) 数组可持久化。注意到这样就不能使用路径压缩，因为路径压缩的复杂度是均摊的，而可持久化不允许均摊复杂度，所以只能按秩合并。按秩合并有按照深度和按照大小两种方式，两种方式是平替的，下文采用按照深度的方式。

什么？你想用 rope 水过？算了吧，会被卡，真的。

代码实现相当于就是把普通的数组换成了可持久化数组，可以类比一下，很好理解。

constexpr int MAXN=2e5+5;
int n,m,rt[MAXN];
struct{
	#define lp st[p].lc
	#define rp st[p].rc
	struct SegTree{
		int lc,rc,fa,dep;
	}st[MAXN<<5];
	int tot;
	void build(int s,int t,int&p){
		p=++tot;
		if(s==t) return st[p].fa=s,void();
		int mid=(s+t)>>1;
		build(s,mid,lp),build(mid+1,t,rp);
	}
	void chgd(int x,int s,int t,int&p){
		st[++tot]=st[p],p=tot;
		if(s==t) return st[p].dep++,void();
		int mid=(s+t)>>1;
		if(x<=mid) chgd(x,s,mid,lp);
		else chgd(x,mid+1,t,rp);
	}
	void chgf(int x,int k,int s,int t,int&p){
		st[++tot]=st[p],p=tot;
		if(s==t) return st[p].fa=k,void();
		int mid=(s+t)>>1;
		if(x<=mid) chgf(x,k,s,mid,lp);
		else chgf(x,k,mid+1,t,rp);
	}
	int ask(int x,int s,int t,int p){
		if(s==t) return p;
		int mid=(s+t)>>1;
		if(x<=mid) return ask(x,s,mid,lp);
		else return ask(x,mid+1,t,rp);
	}
	int fnd(int x,int p){
		int rt=ask(x,1,n,p);
		if(st[rt].fa==x) return rt;
		return fnd(st[rt].fa,p);
	}
	void mge(int x,int y,int p){
		x=fnd(x,rt[p]),y=fnd(y,rt[p]);
		if(x==y) return;
		if(st[x].dep>st[y].dep) swap(x,y);
		chgf(st[x].fa,st[y].fa,1,n,rt[p]);
		if(st[x].dep==st[y].dep) chgd(st[y].fa,1,n,rt[p]);
	}
	bool chk(int x,int y,int p){
		x=fnd(x,rt[p]),y=fnd(y,rt[p]);
		return st[x].fa==st[y].fa;
	} 
}T;

int main(){
	n=read(),m=read();
	T.build(1,n,rt[0]);
	for(int i=1;i<=m;i++){
		rt[i]=rt[i-1];
		int opt=read();
		switch(opt){
			case 1:{
				int x=read(),y=read();
				T.mge(x,y,i);
				break;
			}case 2:{
				rt[i]=rt[read()];
				break;
			}default:{
				int x=read(),y=read();
				write(T.chk(x,y,i));
				break;
			}
		}
	}
	return fw,0;
}

可持久化平衡树

一般的可持久化平衡树基于 FHQ Treap，因为它分裂和合并的操作相较于旋转更方便于可持久化。

相较于普通平衡树，可持久化平衡树的 split 和 merge 操作中都需要新建节点。然后就和普通平衡树的写法没什么区别了。注意它的空间复杂度并不是严格 \(O(n\log n)\) 的，所以能开大尽量开大，没什么可说的。

rope 过不去的。

代码（P3835【模板】可持久化平衡树）：

constexpr int MAXN=5e5+5;
int n,m,rt[MAXN];
mt19937 wdz(chrono::steady_clock::now().time_since_epoch().count());
struct{
	struct FHQ_Treap{
		int ls,rs,key,pri,siz;
	}t[MAXN<<6];
	int tot;
	int newnode(int x){
		t[++tot].siz=1;
		t[tot].key=x;
		t[tot].pri=wdz();
		return tot;
	}
	int update(int p){
		t[p].siz=t[t[p].ls].siz+t[t[p].rs].siz+1;
		return p;
	}
	void split(int p,int x,int&l,int&r){
		if(!p) return l=r=0,void();
		if(t[p].key<=x){
			t[l=++tot]=t[p];
			split(t[p].rs,x,t[l].rs,r);
			update(l);
		}else{
			t[r=++tot]=t[p];
			split(t[p].ls,x,l,t[r].ls);
			update(r);
		}
	}
	int mge(int l,int r){
		if(!l||!r) return l|r;
		int rt=++tot;
		if(t[l].pri>t[r].pri){
			t[rt]=t[l];
			t[rt].rs=mge(t[rt].rs,r);
		}else{
			t[rt]=t[r];
			t[rt].ls=mge(l,t[rt].ls);
		}
		return update(rt);
	}
	void ins(int q,int&p,int x){
		int l,r;
		split(q,x,l,r);
		p=mge(mge(l,newnode(x)),r);
	}
	void del(int q,int&p,int x){
		int l,r,w;
		split(q,x,l,r);
		split(l,x-1,l,w);
		w=mge(t[w].ls,t[w].rs);
		p=mge(mge(l,w),r);
	}
	int rnk(int p,int x){
		int l,r;
		split(p,x-1,l,r);
		int res=t[l].siz+1;
		p=mge(l,r);
		return res;
	}
	int kth(int p,int k){
		if(k==t[t[p].ls].siz+1) return t[p].key;
		if(k<=t[t[p].ls].siz) return kth(t[p].ls,k);
		return kth(t[p].rs,k-t[t[p].ls].siz-1);
	}
	int pre(int p,int x){
		int l,r;
		split(p,x-1,l,r);
		int res=kth(l,t[l].siz);
		p=mge(l,r);
		return !l?INT_MIN+1:res;
	}
	int nxt(int p,int x){
		int l,r;
		split(p,x,l,r);
		int res=kth(r,1);
		p=mge(l,r);
		return !r?INT_MAX:res;
	}
}T;

int main(){
	n=read();
	for(int i=1;i<=n;i++){
		int v=read(),opt=read(),x=read();
		rt[i]=rt[v]; 
		switch(opt){
			case 1:{
				T.ins(rt[i],rt[i],x);
				break;
			}case 2:{
				T.del(rt[i],rt[i],x);
				break;
			}case 3:{
				write(T.rnk(rt[i],x));
				break;
			}case 4:{
				write(T.kth(rt[i],x));
				break;
			}case 5:{
				write(T.pre(rt[i],x));
				break;
			}default:{
				write(T.nxt(rt[i],x));
				break;
			}
		}
	}
	return fw,0;
}

应用

P5055 【模板】可持久化文艺平衡树

比普通的可持久化平衡树多了一个懒标记，只需在下放标记的时候把左右儿子复制一遍即可。

rope 可水过。

constexpr int MAXN=2e5+5;
int n,m,rt[MAXN];
mt19937 wdz(chrono::steady_clock::now().time_since_epoch().count());
struct{
	struct FHQ_Treap{
		int ls,rs,key,pri,siz,lazy;
		ll sum;
	}t[MAXN<<7];
	int tot;
	int newnode(int x){
		t[++tot].siz=1;
		t[tot].key=t[tot].sum=x;
		t[tot].pri=wdz();
		return tot;
	}
	int update(int p){
		t[p].siz=t[t[p].ls].siz+t[t[p].rs].siz+1;
		t[p].sum=t[t[p].ls].sum+t[t[p].rs].sum+t[p].key;
		return p;
	}
	void pushdown(int p){
		if(!t[p].lazy) return;
		if(t[p].ls) t[++tot]=t[t[p].ls],t[p].ls=tot;
		if(t[p].rs) t[++tot]=t[t[p].rs],t[p].rs=tot;
		swap(t[p].ls,t[p].rs);
		t[t[p].ls].lazy^=1;
		t[t[p].rs].lazy^=1;
		t[p].lazy=0;
	}
	void split(int p,int x,int&l,int&r){
		if(!p) return l=r=0,void();
		pushdown(p);
		if(t[t[p].ls].siz+1<=x){
			t[l=++tot]=t[p];
			split(t[p].rs,x-t[t[p].ls].siz-1,t[l].rs,r);
			update(l);
		}else{
			t[r=++tot]=t[p];
			split(t[p].ls,x,l,t[r].ls);
			update(r);
		}
	}
	int mge(int l,int r){
		if(!l||!r) return l|r;
		pushdown(l),pushdown(r);
		int rt=++tot;
		if(t[l].pri>t[r].pri){
			t[rt]=t[l];
			t[rt].rs=mge(t[rt].rs,r);
		}else{
			t[rt]=t[r];
			t[rt].ls=mge(l,t[rt].ls);
		}
		return update(rt);
	}
	void ins(int q,int&p,int x,int y){
		int l,r;
		split(q,x,l,r);
		p=mge(mge(l,newnode(y)),r);
	}
	void del(int q,int&p,int x){
		int l,r,w;
		split(q,x,l,r);
		split(l,x-1,l,w);
		w=mge(t[w].ls,t[w].rs);
		p=mge(mge(l,w),r);
	}
	void flp(int&p,int x,int y){
		int l,r,w;
		split(p,x-1,l,r);
		split(r,y-x+1,w,r);
		t[w].lazy^=1;
		p=mge(mge(l,w),r);
	}
	ll ask(int p,int x,int y){
		int l,r,w;
		split(p,x-1,l,r);
		split(r,y-x+1,w,r);
		ll res=t[w].sum;
		p=mge(mge(l,w),r);
		return res;
	}
}T;

int main(){
	n=read();
	ll lst=0;
	for(int i=1,v,opt,x,y;i<=n;i++){
		v=read(),opt=read(),x=read()^lst;
		if(opt!=2) y=read()^lst;
		rt[i]=rt[v]; 
		switch(opt){
			case 1:{
				T.ins(rt[i],rt[i],x,y);
				break;
			}case 2:{
				T.del(rt[i],rt[i],x);
				break;
			}case 3:{
				T.flp(rt[i],x,y);
				break;
			}default:{
				write(lst=T.ask(rt[i],x,y));
				break;
			}
		}
	}
	return fw,0;
}

[HDU6087] Rikka with Sequence

多出了一个操作 2，实际上对于操作 2 l r k 相当于把 \([l-k,l-1]\) 这个区间一直复制，直到填满 \([l-k,r]\) 这个区间。可以考虑倍增优化它。至于坑人的 64MiB 空间，需要我们在节点数量过大的时候暴力重构整棵平衡树，同时还要进行内存回收。

还有需要注意的是，这题因为使用倍增优化，导致它的重复合并次数比较多，如果使用正常的随机权值方法来合并会挂掉，所以只能采用一种特殊的方式来合并它，具体见代码。但是在正常的题目中，这样写的复杂度不一定更优。

using ll=long long;
constexpr int MAXN=2e5+5;
int n,m,a[MAXN],rt[2];
mt19937 wdz(chrono::steady_clock::now().time_since_epoch().count());
struct{
	struct FHQ_Treap{
		int ls,rs,key,siz;
		ll sum;
	}t[MAXN<<3];
	int tot,tim;
	int stk[MAXN<<3],top;
	int used[MAXN<<3],cnt;
	int vis[MAXN<<3];
	int newnode(int x=0){
		int tt=(top?stk[top--]:++tot);
		used[++cnt]=tt;
		t[tt].ls=t[tt].rs=0;
		t[tt].siz=1;
		t[tt].key=t[tt].sum=x;
		return tt;
	}
	int update(int p){
		t[p].siz=t[t[p].ls].siz+t[t[p].rs].siz+1;
		t[p].sum=t[t[p].ls].sum+t[t[p].rs].sum+t[p].key;
		return p;
	}
	void split(int p,int x,int&l,int&r){
		if(!p) return l=r=0,void();
		if(t[t[p].ls].siz+1<=x){
			l=newnode();
			t[l]=t[p];
			split(t[p].rs,x-t[t[p].ls].siz-1,t[l].rs,r);
			update(l);
		}else{
			r=newnode();
			t[r]=t[p];
			split(t[p].ls,x,l,t[r].ls);
			update(r);
		}
	}
	int mge(int l,int r){
		if(!l||!r) return l|r;
		int rt=newnode();
		if(wdz()%(t[l].siz+t[r].siz)<t[l].siz){
			t[rt]=t[l];
			t[rt].rs=mge(t[rt].rs,r);
		}else{
			t[rt]=t[r];
			t[rt].ls=mge(l,t[rt].ls);
		}
		return update(rt);
	}
	int build(int l,int r){
		if(l>r) return 0;
		int mid=(l+r)>>1,rt=newnode(a[mid]);
		t[rt].ls=build(l,mid-1);
		t[rt].rs=build(mid+1,r);
		return update(rt);
	}
	void dfs(int u){
		if(!u) return;
		vis[u]=tim;
		dfs(t[u].ls),dfs(t[u].rs);
	}
	void rebuild(){
		tim++;
		dfs(rt[0]),dfs(rt[1]);
		int ntot=0;
		for(int i=1;i<=cnt;i++)
			if(vis[used[i]]!=tim) stk[++top]=used[i];
			else used[++ntot]=used[i];
		cnt=ntot;
	}
	ll ask(int p,int x,int y){
		int l,r,w;
		split(p,x-1,l,r);
		split(r,y-x+1,w,r);
		ll res=t[w].sum;
		p=mge(mge(l,w),r);
		return res;
	}
	void mdf(int&p,int x,int y,int k){
		int r1,r2,r3,r4,r5,r6;
		split(p,y,r1,r4);
		split(r1,x-1,r1,r3);
		split(r1,x-k-1,r1,r2);
		r5=r2,r3=0;
		int b=(y-x+1)/k+1;
		while(b){
			if(b&1) r3=mge(r3,r5);
			r5=mge(r5,r5);
			b>>=1;
		}
		split(r3,y-x+1,r3,r6);
		p=mge(mge(mge(r1,r2),r3),r4);
	}
	void cpy(int q,int&p,int x,int y){
		int r1,r2,r3,r4,r5,r6;
		split(q,y,r1,r3);
		split(r1,x-1,r1,r2);
		split(p,y,r4,r6);
		split(r4,x-1,r4,r5);
		p=mge(mge(r4,r2),r6);
	}
}T;

int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	rt[0]=rt[1]=T.build(1,n);
	while(m--){
		int op=read(),x=read(),y=read();
		switch(op){
			case 1:{
				write(T.ask(rt[1],x,y));
				break;
			}case 2:{
				T.mdf(rt[1],x,y,read());
				break;
			}default:{
				T.cpy(rt[0],rt[1],x,y);
				break;
			}
		}
		if(T.cnt>=1.5e6) T.rebuild();
	}
	return fw,0;
}

可持久化字典树

和上面两种结构的可持久化方式基本一致。在一次修改中，对于需要修改的节点进行修改，没有动的节点继续复用之前的节点即可。

可持久化字典树的主要应用就是求最大异或和问题。具体来说，这类问题的形式为：给定一个数列和 \(l,r,x\)，求 \(\max\limits_{l\le k\le r}\{a_k\oplus x\}\)。所以可持久化字典树中需要给每个节点记录一个 \(\mathit{val}\) 值表示当前点被多少个版本使用，从而在查询的时候直接相减即可。

代码：（P4735 最大异或和）

#include<bits/stdc++.h>
using namespace std;

constexpr int MAXN=6e5+5;
int n,m,a[MAXN],rt[MAXN];
struct{
	struct Trie{
		int c[2],val;
		int& operator[](int x){
			return c[x];
		}
	}t[MAXN<<5];
	int tot;
	void ins(int x,int q,int p){
		for(int i=25;~i;i--){
			int c=x>>i&1;
			if(!t[p][c]) t[p][c]=++tot;
			t[p][!c]=t[q][!c];
			t[p].val=t[q].val+1;
			p=t[p][c],q=t[q][c];
		}
		t[p].val=t[q].val+1;
	}
	int ask(int x,int q,int p){
		int res=0;
		for(int i=25;~i;i--){
			int c=x>>i&1;
			if(t[t[p][!c]].val-t[t[q][!c]].val) res+=1<<i,p=t[p][!c],q=t[q][!c];
			else p=t[p][c],q=t[q][c];
		}
		return res;
	}
}T;

int main(){
	cin.tie(nullptr)->sync_with_stdio(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		a[i]^=a[i-1];
		rt[i]=++T.tot;
		T.ins(a[i],rt[i-1],rt[i]);
	}
	while(m--){
		char c;
		cin>>c;
		if(c=='A'){
			cin>>a[++n];
			a[n]^=a[n-1];
			rt[n]=++T.tot;
			T.ins(a[n],rt[n-1],rt[n]);
		}else{
			int l,r,x;
			cin>>l>>r>>x;
			l--,r--;
			if(!l) cout<<max(a[n]^x,T.ask(a[n]^x,rt[0],rt[r]))<<'\n';
			else cout<<T.ask(a[n]^x,rt[l-1],rt[r])<<'\n';
		}
	}
	return 0;
}

应用

P4098 [HEOI2013] ALO

重点是如何找出一个区间的次大值。显然不好做，套路地转化为针对每个数求其作为次大值的区间。这里方法比较多，比较简单的实现方式是使用链表，从小到大依次删数，那么到某个数时比它小的数一定都已被删完，我们就可以方便地求出其向左或向右第一个和第二个比它大的数的位置。不妨从左到右依次记为 \(l_2,l_1,r_1,r_2\)，容易发现使当前数为区间最大值的极大区间为 \((l_2,r_1)\) 和 \((l_1,r_2)\)，分别在这两个区间求最大异或和即可。

P10690 Fotile 模拟赛 L

考虑分块，预处理每个块中的最大连续异或和。块与块之间显然可以 \(O(1)\) 转移。然后对于每个询问中的散块暴力，整块直接获取答案，求最大值即可。只要对可持久化字典树有充分理解就很简单。

P5795 [THUSC 2015] 异或运算

发现题目中 \(n,p\) 的数据范围是一个 \(O(n^2)\) 复杂度，启示我们要暴力枚举每一行的贡献。然后发现求区间 \(k\) 大值，考虑可持久化字典树上二分。具体来说，为了答案尽可能大，就是先判断与当前位不同的一边的 \(\mathit{val}\) 值之和，如果比 \(k\) 大说明这一位可以提供贡献，累加贡献然后扫这一边；否则扫另一边。注意在同一时刻每行的根可能是不同的，所以需要给每行开一个数组记录当前行的根。