后缀自动机 SAM
后缀自动机 SAM
约定:字符串下标从 \(1\) 开始。
后缀自动机是一个强有力的数据结构,能在线性时间内解决以下这些关于字符串的问题。
- 在一个字符串中搜索另一个字符串的所有出现位置。
- 计算给定的字符串中有多少个不同的子串。
容易发现,这些问题都和 “子串” 有关。事实上,后缀自动机能解决的问题基本都能转化成 “子串” 相关问题。
引入
根据我们的经验,处理一个字符串的有效方式是找出后缀。之前使用后缀数组找出后缀,但是后缀数组基本只能处理静态问题,一旦变成动态,后缀数组的动态更新是极为乏力的。
我们尝试运用自动机来处理后缀,这就是后缀自动机(Suffix Automaton),简称 SAM。它的时间是 \(O(N)\),空间是 \(O(N|\Sigma|)\),其中 \(|\Sigma|\) 是字符集大小。
概念
之前讨论过的自动机,诸如 AC 自动机和 PAM,它们的形态都类似于一棵 Trie 的形式,然后在其上添加了一些指针。而 SAM 比较特殊,它的形态是一个 DAG。因为,在一棵 Trie 上直接存储后缀是很浪费时间和空间的,约为 \(O(N^2)\)。而我们不需要开那么多无用的节点,只需用类似下图这样紧凑的存储方式即可:
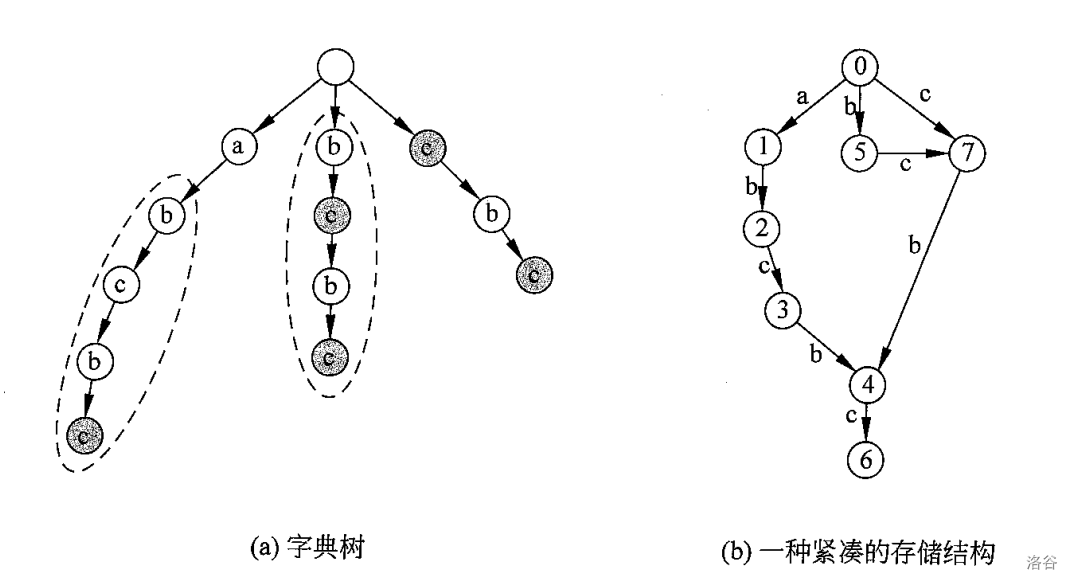
如何构造这种紧凑的 DAG 存储我们暂且不表。我们只需知道,这个 DAG 构建巧妙地利用了子串之间的包含关系,省去了重合的部分,因此大大减少了空间。
事实上,这种新的存储结构的节点数量不会超过 \(2N\),比原来优秀得多。
endpos 和等价类
这种 DAG 存储方式优化的关键在于,找出所有子串的右端点结束位置来处理子串之间的包含关系。我们把右端点结束位置记为 \(\rm endpos\)。
求所有子串的 endpos
定义 \(\text{endpos}(T)\) 为子串 \(T\) 在原字符串 \(S\) 中所有出现的位置的集合。下面举例说明。
以 \(S=\tt abcbc\) 为例,这个字符串一共有 \(12\) 个子串,每个子串的 \(\rm endpos\) 如下:
令空集 \(\varnothing\) 的 \(\text{endpos}=\{1,2,3,4,5\}\),并按照 \(\rm endpos\) 的种类进行排序,得到:
我们把 \(\rm endpos\) 相等的子串称为等价类,比如 \(\tt c\) 和 \(\tt bc\) 就是等价类。容易发现,除了 \(\varnothing\),一共有 \(7\) 个等价类。
等价类的性质
等价类的一些性质是后续解题的关键。
- 同一个等价类中较短子串是较长子串的后缀。
- 同一个等价类中的子串长度不等,且依次递增 \(1\),覆盖了从最短子串到最长子串的区间。
- 若一个子串 \(v\) 是另一个子串 \(u\) 的后缀,则有 \(\text{endpos}(u)\subseteq\text{endpos}(v)\)。
- 等价类的数量不超过 \(2N\)。
这些性质中,性质 3 应该是最重要的。这让我们可以根据等价类把 SAM 重构成一棵树的形式,我们把这棵树称为 parent 树(母树)。
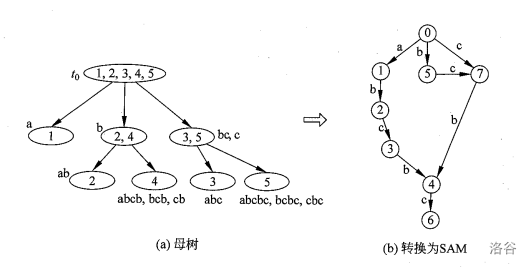
这棵母树又有很多有用的性质,我们暂且不表,先考虑怎么构建出右图这个 SAM。
构建 SAM
事实上,构建 SAM 的过程和母树是息息相关的。
后缀链 link/fa
考虑 SAM 上的一个不是根的节点 \(v\),它的 \(\rm link\) 定义为它上层的一个节点 \(u\),其中 \(u\) 的等价类所包含的子串也是 \(v\) 所包含的子串的后缀。其实就是上文母树上每个点的父亲,现在对于 SAM 上的每个节点需要存储下来这个 \(\rm link\)。
建 SAM
每次往 SAM 里插入原串的一个字符,直到所有的字符都加入 SAM。建 SAM 的关键在于:
- 起点和终点之间的边代表在当前字符串之后增加一个字符。
- 从根到达图中任意点的路径形成的子串是 \(S\) 中的一个子串。
- 保证每个点的所有子串属于同一个等价类。
- 点之间符合母树的父子关系。也就是符合母树的性质,包括到达 \(u\) 的所有字符串长度都严格大于到达 \(\text{link}(u)\) 的所有字符串长度,以及到达 \(\text{link}(u)\) 的任意子串一定是到达 \(u\) 的任意子串的后缀。
// 背板!
struct SAM{
int len,fa,s[26];
}sam[MAXN];
void ins(int i){
sam[++tot].len=sam[lst].len+1;
int pos=lst,ch=s[i]-'a';
lst=tot;
while(pos&&!sam[pos].s[ch]){
sam[pos].s[ch]=tot;
pos=sam[pos].fa;
}
if(!pos) sam[tot].fa=1;
else{
int p=pos,q=sam[pos].s[ch];
if(sam[p].len+1==sam[q].len) sam[tot].fa=q;
else{
sam[++tot]=sam[q];
sam[tot].len=sam[p].len+1;
sam[q].fa=sam[lst].fa=tot;
while(pos&&sam[pos].s[ch]==q){
sam[pos].s[ch]=tot;
pos=sam[pos].fa;
}
}
}
}
因为等价类的数量是 \(2N\),所以这里的 MAXN 应当开两倍。
注意如果所求字符串的字符集大小比较大,应当使用 map 来存储,复杂度也相应地多了一个 \(\log\)。
不要使用 unordered_map。
SAM 的一些性质
- 每次插完一个字符之后,\(\mathit{lst}\) 就是这个字符在 SAM 中的位置。
- 构造出 SAM 之后,如果连接所有的 \(\text{fa}(u)\to u\) 的边,就是上文所提到的母树。
SAM 的应用
子串出现次数
典型例题:P3804 【模板】后缀自动机(SAM)。
对 \(S\) 构建出 SAM,考虑某个等价类中的字符串出现过的次数就是这个等价类的 \(\rm endpos\) 集合大小,又因为每次增加了一个字符会增加一堆后缀,要维护这些后缀的出现次数只需每次在 \(\mathit{lst}\) 的位置设置 \(\text{siz}=1\)。建立 SAM 之后再建出母树,在母树上用树形 DP 统计 \(\text{siz}\),对于所有出现次数不为 \(1\) 的节点统计答案。
不同子串个数
典型例题:P4070 [SDOI2016] 生成魔咒。
对 \(S\) 构建出 SAM,考虑 SAM 上的每个节点能带来多少不同的子串,显然每新增一个字符所增加的不同子串只能是当前的后缀,而当前后缀中位于 \(\text{link}(u)\) 的等价类的后缀已经出现过了,所以一个节点能带来新的不同子串就是 \(\text{len}(u)-\text{len}(\text{link}(u))\),对所有节点求和即可。
第 k 小子串
典型例题:P3975 [TJOI2015] 弦论。
考虑 SAM 上的一条路径就是一个子串,所以第 \(k\) 小子串就是 SAM 上的第 \(k\) 小路径。每个节点的排名应当是从它出发所能到达的点的 \(\text{siz}\) 之和。然后需要根据题目要求来分析,如果相同的子串算一个,那么每一个节点都能提供 \(1\) 的排名,\(\text{siz}\) 设置为 \(1\);如果相同的子串算多个,每个节点能提供的排名就需要通过问题 1 的方法树形 DP 求出 \(\text{siz}\)。把这个值放到 SAM 上,对于询问只需走到排名等于当前排名的地方即可。
最长公共子串
对于两个串,可以对其中一个建出 SAM,对另外一个在 SAM 上跑匹配:如果能匹配上就给答案 \(+1\),否则就一直跳 \(\text{link}\) 直到能匹配上,然后计算答案。这个方法事实上可以处理出匹配串的每个前缀在原串上的出现次数,就是代码中的 \(w_i\)。用在了熟悉的文章这道题里面。
void initw(){
int lst=0,pos=1;
for(int i=1;i<=n;i++){
int c=s[i]-'0';
if(sam[pos].s[c]) lst++,pos=sam[pos].s[c];
else{
while(pos&&!sam[pos].s[c]) pos=sam[pos].fa;
if(!pos) lst=0,pos=1;
else lst=sam[pos].len+1,pos=sam[pos].s[c];
}
w[i]=lst;
}
}
对于 \(n\) 个串,见 “广义 SAM”。
最长公共前缀(LCP)
典型例题:P4248 [AHOI2013] 差异。
首先套路地把原字符串反转,原问题就变成了一个最长公共后缀问题。因为母树上父亲的子串一定是儿子的子串的后缀,所以最长公共后缀就是母树上两点的 LCA。
对于这道例题而言,直接枚举两点然后求 LCA 是 \(O(n^2\log n)\) 的,必定不可取;考虑求每个 LCA 能给多少对点带来贡献,这就是一个典型的树形 DP 问题了。
一些其他的 trick
- 线段树合并可以维护出 endpos 集合,因为 SAM 上每个点的 \(\text{endpos}\) 集合都是它母树上的儿子的 \(\text{endpos}\) 集合之并。用线段树合并维护出每个点的 \(\text{endpos}\) 集合(有时需要一些其他的相关信息),在一些较难的 SAM 题中用于选定一个特定区间的答案。如你的名字、字符串这两道题。
- 如果遇到需要定位 \([l,r]\) 这个子串在 SAM 上或在母树上的位置,可以先找出 \([1,r]\) 的前缀所对应的节点,然后用在母树上用倍增找到第一个长度大于等于 \(r-l+1\) 的点,这个点就是 \([l,r]\) 这个子串所对应的点。如字符串这道题。
- 对于所有不同的 \(\text{endpos}\) 集合,它相邻的位置对的数量是 \(O(n\log n)\) 的。遇到查询在一个区间 \([l,r]\) 的询问时,可以用启发式合并找出不同的贡献对,这个贡献对的数量也是 \(O(n\log n)\) 的。比如事情的相似度这道题。
- SAM 还能和虚树套在一起,比如 SvT 这道题。
广义 SAM
广义 SAM 用于解决多个字符串之间的问题。具体而言,是对多个字符串先建出一个 Trie,然后对这个 Trie 构造 SAM。各种各样的伪广义 SAM 不推荐学习。
通常的构造方法是离线 BFS。
// 背板!
struct{
int tot=1;
struct Trie{
int fa,c,s[26];
}t[MAXN];
void ins(const string&s){
int p=1;
for(auto x:s){
int c=x-'a';
if(!t[p].s[c]){
t[p].s[c]=++tot;
t[tot].fa=p,t[tot].c=c; // 略有不同
}
p=t[p].s[c];
}
}
}T;
struct{
int tot=1;
struct SAM{
int len,fa,s[26];
}sam[MAXN];
int ins(int x,int lst){ // 略有不同
sam[++tot].len=sam[lst].len+1;
int pos=lst,ch=T.t[x].c;
lst=tot;
while(pos&&!sam[pos].s[ch]){
sam[pos].s[ch]=tot;
pos=sam[pos].fa;
}
if(!pos) sam[tot].fa=1;
else{
int p=pos,q=sam[pos].s[ch];
if(sam[p].len+1==sam[q].len) sam[tot].fa=q;
else{
sam[++tot]=sam[q];
sam[tot].len=sam[p].len+1;
sam[q].fa=sam[lst].fa=tot;
while(pos&&sam[pos].s[ch]==q){
sam[pos].s[ch]=tot;
pos=sam[pos].fa;
}
}
}
return lst;
}
void build(){
queue<pair<int,int>>q;
for(int i=0;i<26;i++)
if(T.t[1].s[i])
q.emplace(T.t[1].s[i],1);
while(!q.empty()){
int u=q.front().first,lst=q.front().second;
q.pop();
int now=ins(u,lst);
ans+=sam[now].len-sam[sam[now].fa].len;
for(int i=0;i<26;i++)
if(T.t[u].s[i])
q.emplace(T.t[u].s[i],now);
}
}
}S;
应用
最长公共子串
对于找一个串出现在多个模板串上的最长长度,仍然套用上文中的方法。
否则就是最直接的最长公共子串问题,典型例题:P2463 [SDOI2008] Sandy 的卡片。
对于 SAM 上的每个节点都建立一个长度为 \(n\) 的数组 \(\text{siz}\),其中 \(\text{siz}(i)\) 表示当前节点是第 \(i\) 个串的子串。这个 \(\text{siz}\) 可以是布尔数组,也可以是计数数组,根据具体题目而定。最后统计满足 \(\forall\text{siz}(i)=1\) 的节点 \(i\) 的 \(\text{len}\) 的最大值。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号