偏差-方差分解

0、概述

偏差（bias）-方差（Variance）分解是统计学解释学习算法泛化性能的一种重要工具。可以把一种学习算法的期望误差分解为三个非负项的和，即偏差bias、方差variance和样本噪音noise。可以根据分解后每一项的具体值做模型的进一步调整。

1、指标解释

偏差-方差分解中，共涉及到四个重要指标，即泛化误差、偏差、方差和样本噪音。

0）准备数据

D: 训练集，x: 测试集的输入，y：输入x的真实标记，\(y_D\)输入x的样本标记（样本标记可能存在噪声，不一定是真实标记；这里\(y_D\)的下标表示为D指的是测试集样本与训练集样本来自于同一个分布）

\(f(x;D)\)：训练集D上学到的模型在测试集上的输出

\(\bar f(x)=E_D(f(x;D))\)：模型的预测期望输出

备注：这里共有四个不同的输出，分别是：\(y, \space y_D, \space f(x;D), \space \bar f(x)\)

1）泛化误差

在机器学习中用训练数据集去训练一个模型，通常的做法是定义一个误差函数，通过优化函数使误差最小化，从而提高模型的性能。学习模型的目的是为了解决训练数据集这个领域中的一般化问题，单纯地将训练数据集的误差最小化，并不能保证在解决更一般的问题时模型仍然是最优，甚至不能保证模型是可用的。这个模型在该领域的一般化问题中的损失就叫做泛化误差（一般指的是在测试集或验证集上的误差）。以回归算法为例，泛化误差公式为：

\[E(f;P)=E_D[f(x;D)-y_P] \tag{1} \]

2）偏差

期望输出与真实标记的差别称为偏差，记为Bias:

\[bias^2(x)=(\bar f(x) - y)^2 \tag{2} \]

偏差度量了模型的期望值和真实结果的偏离程度，刻画了模型本身的拟合能力

3）方差

不同训练集（样本数相同）产生的模型波动，即模型的不稳定性，记为Variance：

\[var(x)=E_D[((f(x;D)-\bar f(x))^2)] \tag{3} \]

方差度量了同样大小的训练集的变动所导致的学习性能的变化，刻画了数据扰动所产生的影响。

4）噪声

样本的标记值（标记值可能存在噪声）和样本的真实值之间的差异：

\[\varepsilon = E_D[(y - y_D)^2] \]

噪声表达了当前任务上任何学习算法所能达到的期望泛化误差的下界，刻画了学习问题本身的难度。

2、泛化误差分解

对算法的期望泛化误差进行分解：

\[\begin{align} E(f;D) &=E_D[(f(x;D)-y_D)^2] \\ &={\color{Blue} {E_D[(f(x;D)-\overline{f}(x) + \overline{f}(x) - y_D)^2]}} \\ &=E_D[(f(x;D)-\overline{f}(x))^2]+E_D[(\overline{f}(x) - y_D)^2]+{\color{Red} {E_D[2(f(x;D)-\overline{f}(x))(\overline{f}(x) - y_D)]}} \\ &=E_D[(f(x;D)-\overline{f}(x))^2] + {\color{Blue} {E_D[(\overline{f}(x) - y + y - y_D)^2]}} \\ &=E_D[(f(x;D)-\overline{f}(x))^2]+E_D[(\overline{f}(x) - y)^2]+E_D[(y - y_D)^2]+{\color{Red} {E_D[2(\overline{f}(x) - y)(y - y_D)]}} \\ &=E_D[f(x;D)-\overline{f}(x))^2] + (\overline{f}(x)-y)^2 + E_D[(y_D-y)^2] \\ &=var(x) + bias^2(x) + \varepsilon^2 \end{align} \]

会产生疑惑的地方：

\(E_D[(\overline{f}(x) - y)^2] = (\overline{f}(x)-y)^2\)
由于y是数据集x的真实标记，因此是一个固定的值；而\(\overline{f}(x)\)是\(f\)对\(x\)的期望预测输出，也是一个标量，因此\(E_D(标量)=标量\)
公式中两个标红的项，展开后结果为0。利用了\(y_D=y+\varepsilon, \varepsilon不依赖与f，且噪声期望E_D(\varepsilon)=0\)

\[\begin{align} &E_D[2(f(x;D)-\bar{f}(x))(\bar{f}(x) - y_D)] \\ & \varpropto E_D[f(x;D)*\bar{f}(x)]-E_D[\bar{f}(x)*\bar{f}(x)]-E_D[f(x;D)*y_D]+E_D[\bar{f}(x)*y_D] \\ & =\bar{f}(x)*E_D[f(x;D)]-\bar{f}^2(x)-E_D[f(x;D)*(y+\varepsilon)]+E_D[\bar{f}(x)*(y+\varepsilon)]\\ & = \bar{f}(x)*\bar{f}(x)-\bar{f}^2(x)-E_D[f(x;D)*y]-E_D[f(x;D)*\varepsilon]+E_D[\bar{f}(x)*y)]+E_D[\bar f(x)\varepsilon]\\ & = -E_D[f(x;D)*y] + E_D[\bar f(x)*y] \\ & = E_D[(\bar f(x) - f(x;D))*y] \\ & = 0 \end{align} \]

绿色的地方是为了方便后续的计算，对表达式进行展开。

3、偏差-方差窘境

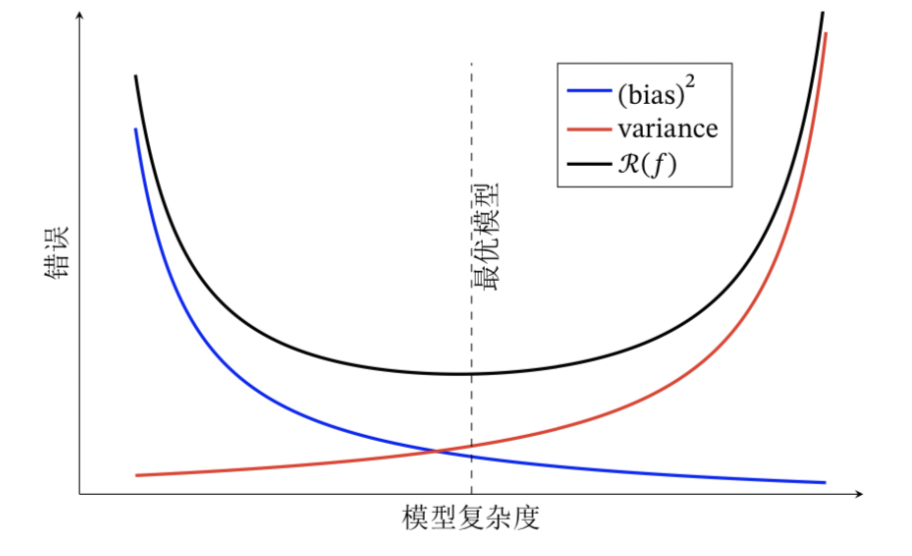
为了得到泛化性能好的模型，我们需要使偏差较小，即能充分拟合数据，并且使方差小，使数据扰动产生的影响小。一般来讲，偏差和方差在一定程度上是有冲突的，这称作为偏差-方差窘境。既要偏差小，又要方差小几乎是不可能的。 下图中的\(R(f)\)是指泛化误差，图中展现了方差、偏差和泛化误差之间的关系。

在模型训练不足时，拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导泛化误差，此时称为欠拟合现象。当随着训练程度加深，模型的拟合能力增强，训练数据的扰动慢慢使得方差主导泛化误差。针对欠拟合，我们提出集成学习的概念并且对于模型可以控制训练程度，比如神经网络加多隐层，或者决策树增加树深。
当训练充足时，模型的拟合能力非常强，数据轻微变化都能导致模型发生变化，如果过分学习训练数据的特点，则会发生过拟合。针对过拟合，我们需要降低模型的复杂度，提出了正则化惩罚项。